「角度の大きさ」を求める難問に挑戦！あなたは解けますか？

問題はこちら

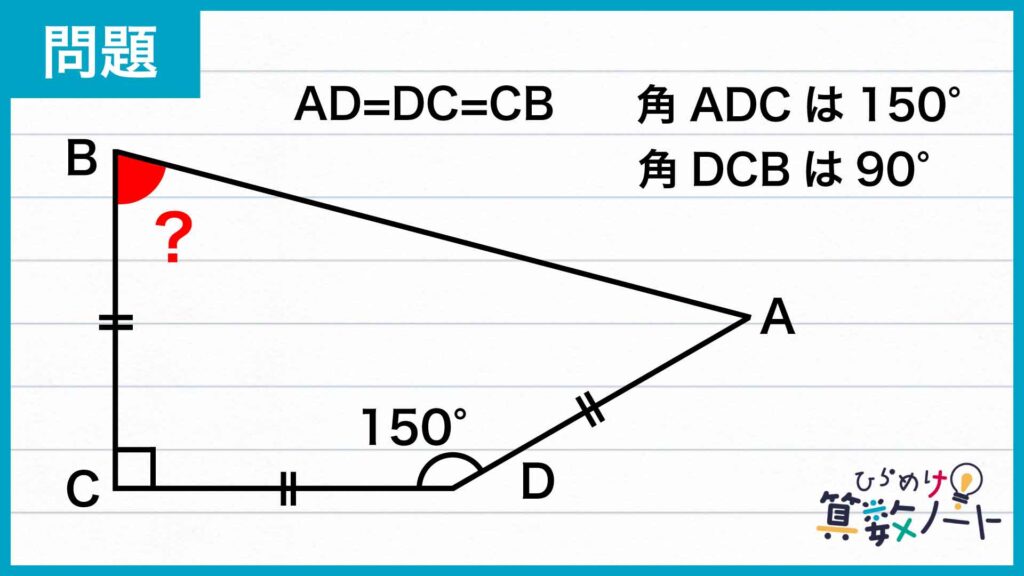
1ページ目：自力で解きたい方はこちらへ！　以下は問題の解説です

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

今回の問題を解くうえで重要なポイントを以下にまとめました。

整理すると、

• 新たに点Eをとる
• 正方形と正三角形の性質を利用する

の2点です。これらのポイントを踏まえながら、問題を解いていきましょう。

新たに点Eをとる

角度の大きさを直接求めることが難しいときには、下の図のように「いくつかの角に分割する方法」か「角度の引き算で求める方法」が有効な場合が多いです。

ここでは、「角度の引き算で求める方法」を利用します。

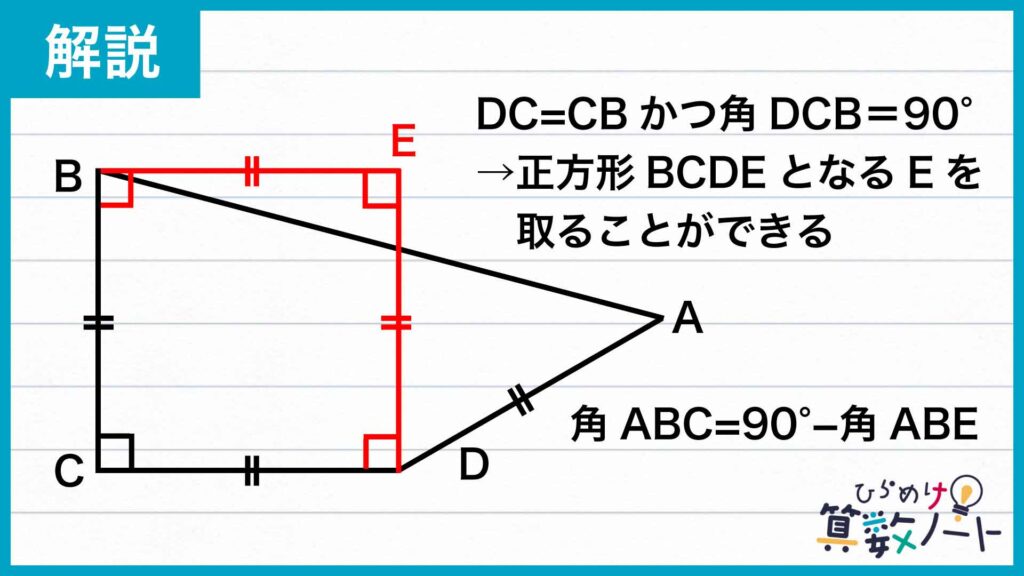
問題文の条件より、DC=CBかつ角DCB=90度ですから、四角形BCDEが正方形になるように点Eを取ることができますね。このように点Eを取ると角EBC=90度となるので、角ABC=角EBC-角ABE=90-角ABE、と求めることができます。

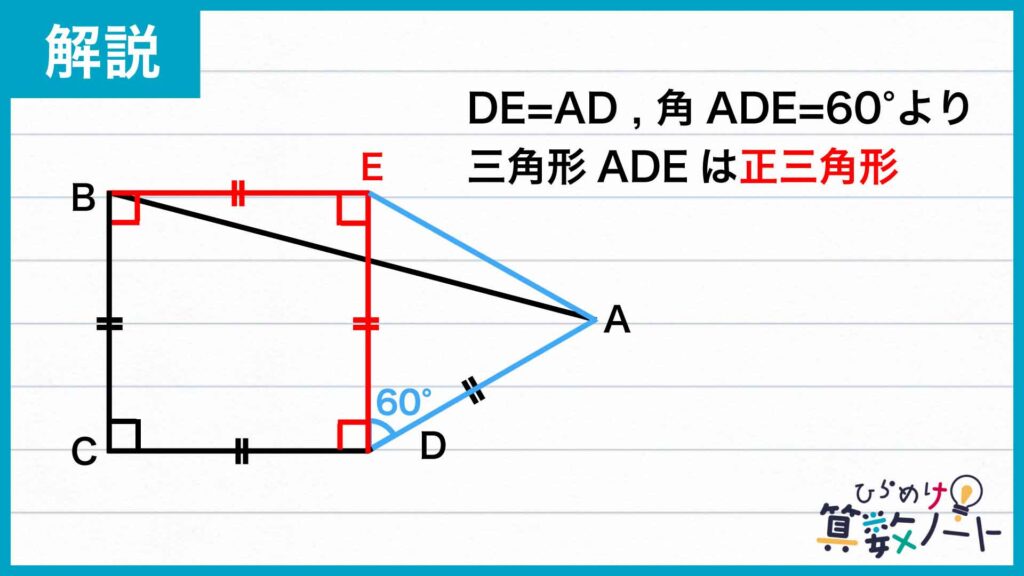
さらに、正方形であることからCD=DEであり、問題文よりCD=ADであることからDE=ADなので、三角形ADEは二等辺三角形です。加えて、問題文から角ADC=150度なので、角ADE=角ADC-角CDE=60度になります。したがって、三角形ADEは頂角（角ADE）の大きさが60度の二等辺三角形であるので、正三角形になることがわかります。

正方形と正三角形の性質を利用する

三角形ADEは正三角形であるので、AE=ADが成り立ちます。さらに、AD=BEであったので、AE=BEです。したがって、三角形ABEも二等辺三角形になることがわかります。

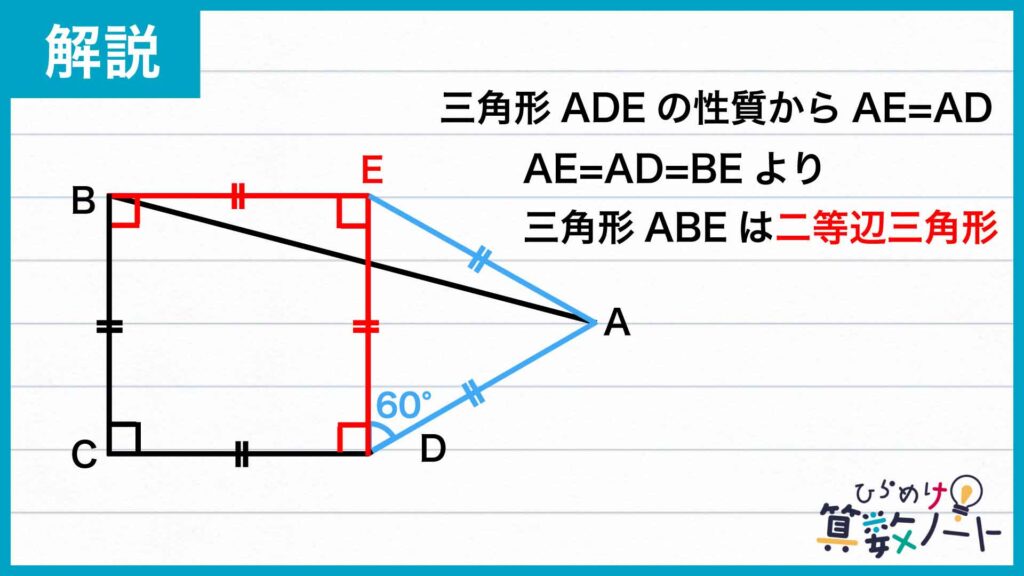
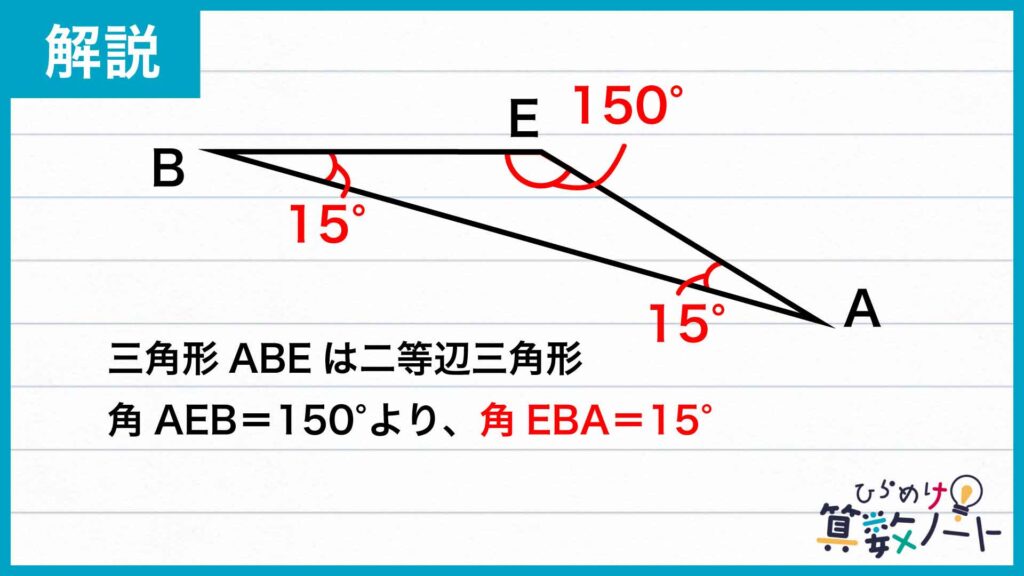
ここで、角AEB=角AED+角BED=60+90=150度であるので、二等辺三角形ABEの頂角（角AEB）の大きさは150度です。よって、角BAE=角ABE=(180-150)÷2=15度になります。

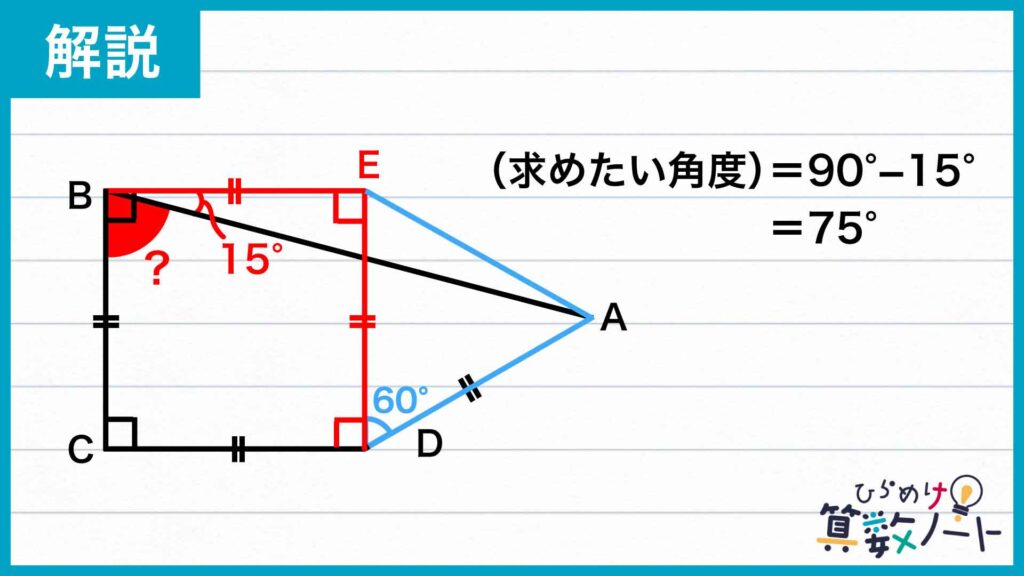
したがって、角ABCの大きさは、角EBCの大きさから角ABEの大きさを差し引くことで、90-15=75度と求められます。

答え：75度

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】