【問題はこちら】
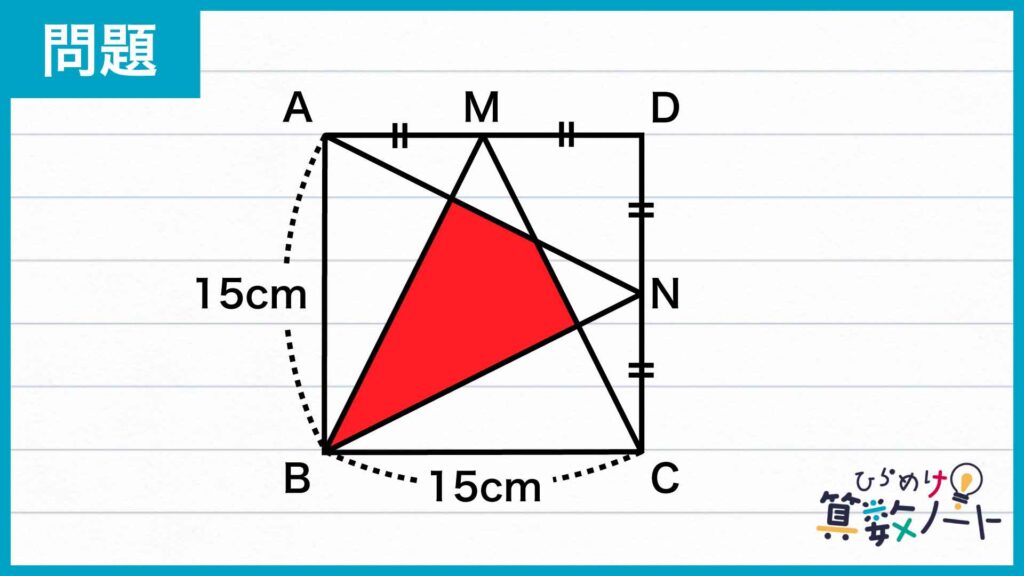
1ページ目:自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の問題の解き方をまとめた図がこちらです。
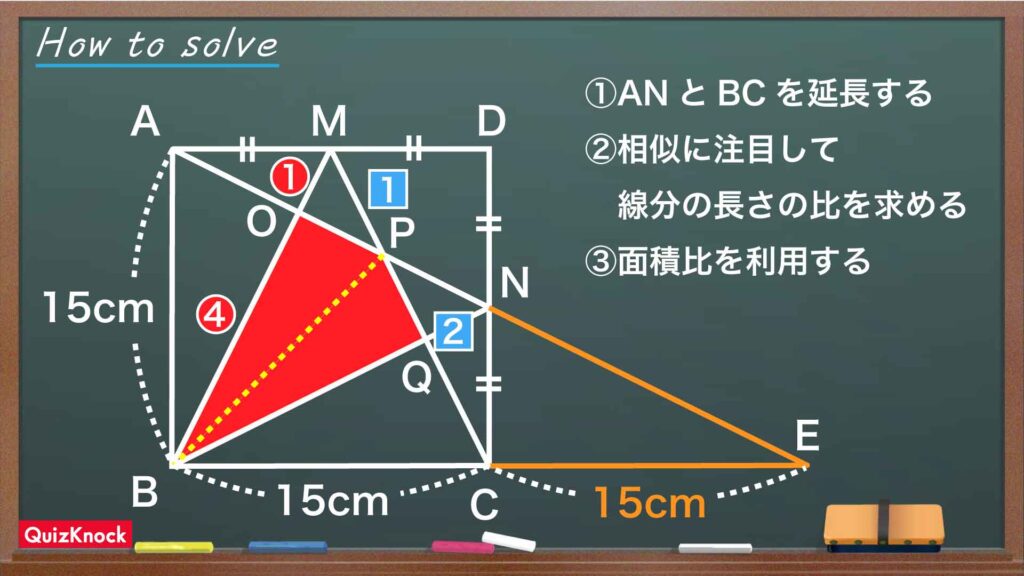
ポイントは、線分の長さの比に注目して、面積比を利用することです。これを踏まえて解いていきましょう!
補助線を引く
次の図のように頂点を振り、補助線を引きます。
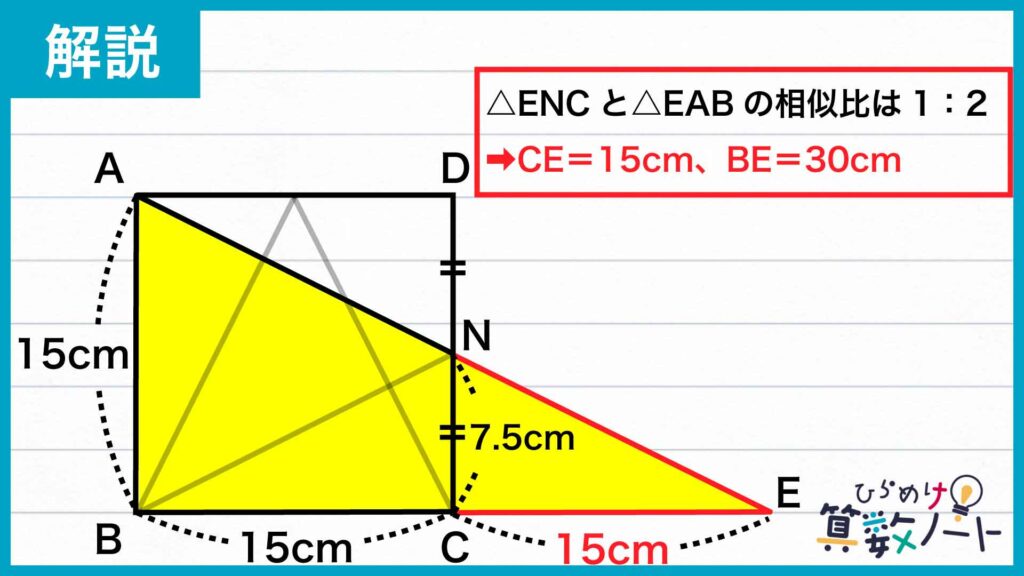
このとき、辺NCと辺ABが平行なので、三角形ENCと三角形EABは相似の関係にあります。点Nは辺CDの中点であるため、線分NCと線分ABの長さの比は1:2であり、線分三角形ENCと三角形EABの相似比は1:2です。
よって、線分ECと線分EBの長さの比は1:2であり、EC=15cm、EB=30cmだとわかります。
相似を利用して線分の長さの比を求める
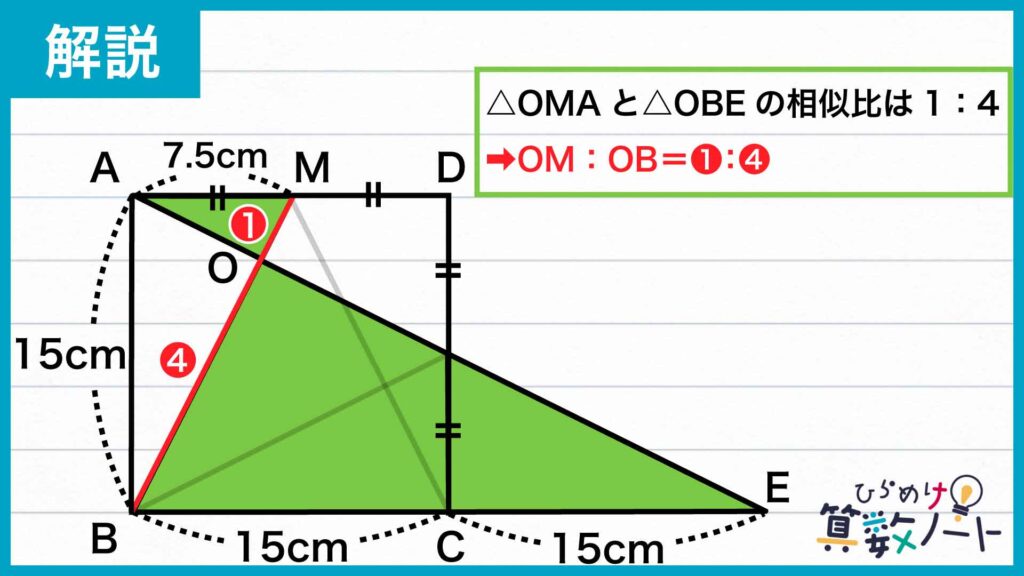
次に、三角形OMAと三角形OBEに注目します。
角AOMと角EOBは対頂角(2本の直線が交わってできる角のうち、互いに向かい合っているもの)の関係にあるため大きさが等しいです。また、辺MAと辺BEは平行なので、平行線についての錯角(2本の直線が別の直線と交わってできる角のうち、斜め向かいに位置するもの)の関係から、角OMA=角OBE、角OAM=角OEBとなります。よって、対応する角の大きさが等しいため、三角形OMAと三角形OBEは相似です。
辺MA=7.5cm、辺BE=30cmなので、相似比は1:4であり、線分OMと線分OBの長さの比は1:4になります。
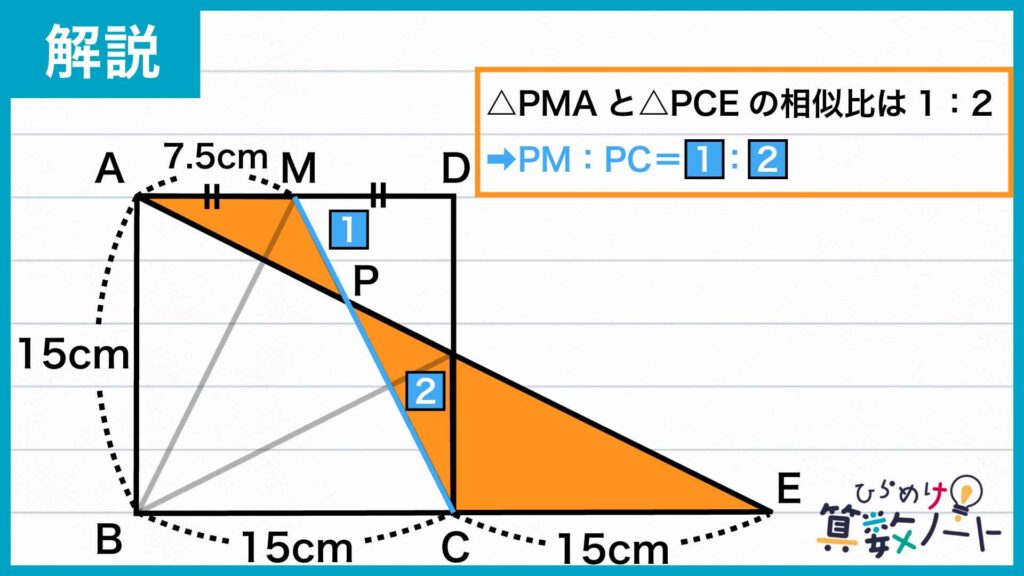
三角形PMAと三角形PCEについても同様に考えると、両者は相似であることがわかります。
辺MAと辺CEの長さの比が1:2なので、線分PMと線分PCの長さの比は1:2です。
図形の対称性に注目する
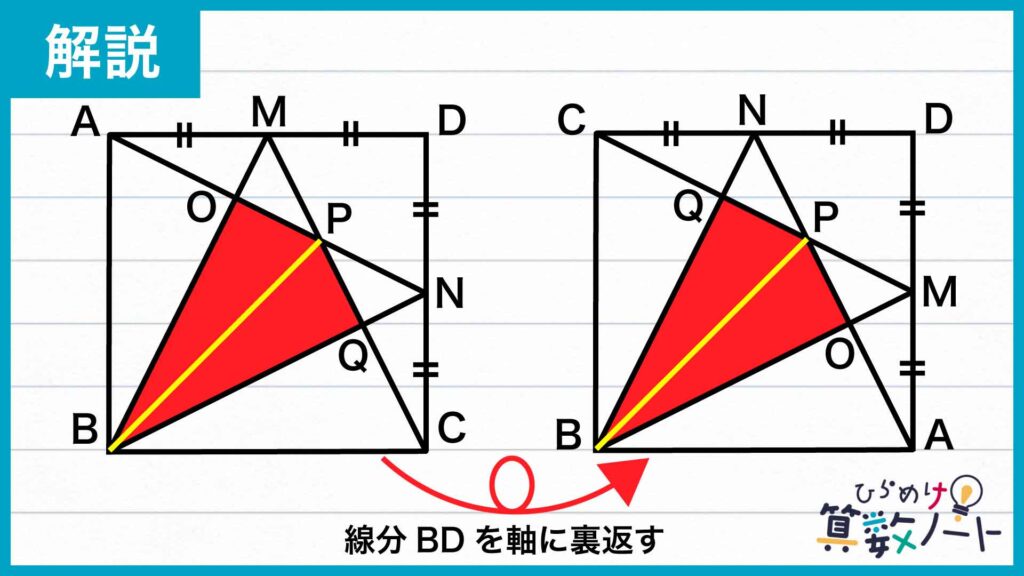
左の図のように線分BPを引き、四角形OBQPを三角形OBPと三角形QBPに分割します。
そして、線分BDを軸に図形全体を裏返してみると、右の図のようになります。
ここから、左右の図形は頂点の名前が異なるだけで、形は全く同じであることがわかります。よって、四角形OBQPの面積は、三角形OBPの面積を2倍すれば求めることができます。
辺の長さの比から面積比を考える
三角形MBCに対して、四角形OBQPが占める面積の割合を考えます。まず、線分PMと線分PCの長さの比が1:2なので、三角形BPMの面積は三角形MBCの1/3倍です。さらに、線分OMと線分OBの長さの比が1:4なので、三角形OBPの面積は三角形BMPの面積の4/5倍です。よって、三角形OBPの面積は三角形MBCの1/3×4/5=4/15倍であり、四角形OBQPの面積はその2倍の8/15倍となります。
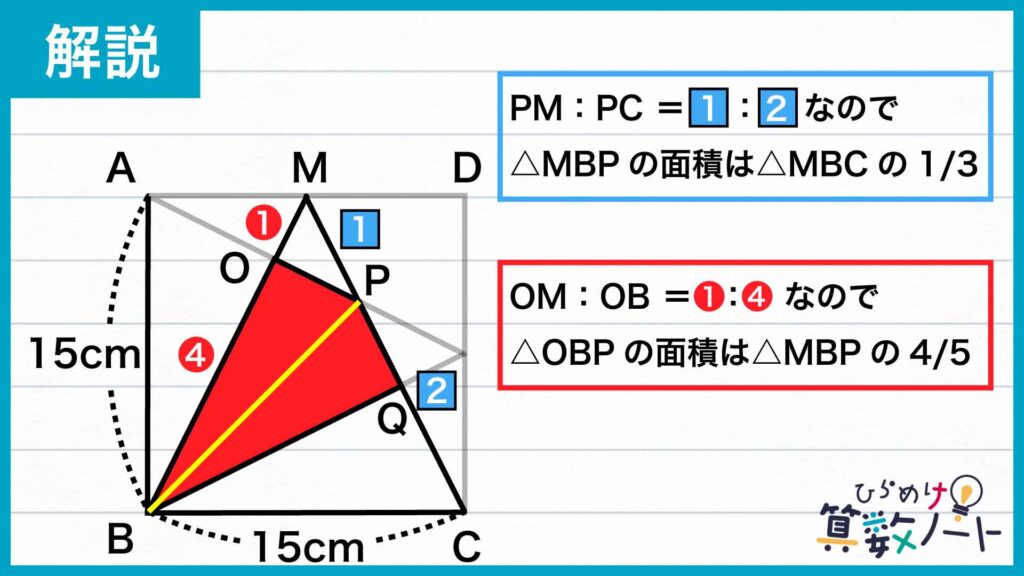
以上より、四角形OBQPの面積は、15×15÷2×8/15=60cm2です。
答え:60cm2それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)








.jpg)







