ひらめけ!算数ノート p.178小学生も解ける「図形の面積」を求める問題、あなたは解けますか?
理系古郡 将也2025.12.24
ヒント
次の図のように頂点を振り、補助線を引きます。
このとき、点Nは辺CDの中点なので、線分NCと線分ABの長さの比は1:2であり、三角形ENCと三角形EABの相似比は1:2です。
よって、線分CEの長さは15cmであり、線分BEの長さは15+15=30cmとなります。MA=7.5cm、BE=30cmなので、三角形OMAと三角形OBEは相似比が1:4であり、線分OMと線分OBの長さの比は1:4です。
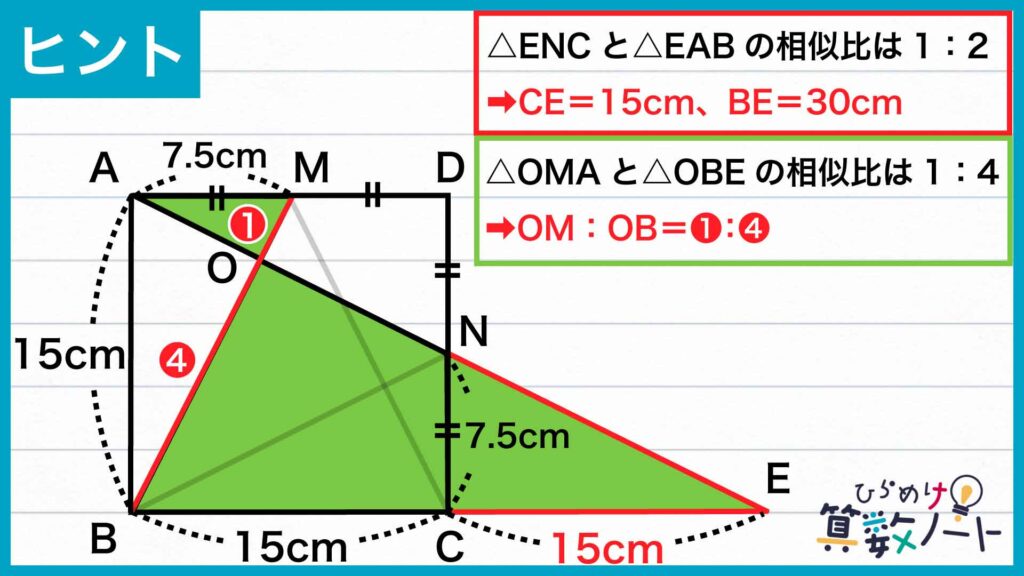
三角形PMAと三角形PCEについても同様に考えると、線分PMと線分PCの長さの比は1:2だとわかります。

四角形のままでは面積が求めにくいので、ここから四角形OBQPを分割してみましょう!
3ページ目:【答え&解説】線分の長さの比から面積比を考えましょう! 答えと解説はこちらへ
Amazonのアソシエイトとして、当サイトは適格販売により収入を得ています。
関連記事
この記事を書いた人

古郡 将也
東京科学大学医学部4年生の古郡将也(ふるごおり・まさや)です。
ピアノ、プログラミング、さらば青春の光などが好きです。
読んでいて面白くてためになる記事を書きたいです。
よろしくお願いします!
古郡 将也の記事一覧へ




















.jpg)







