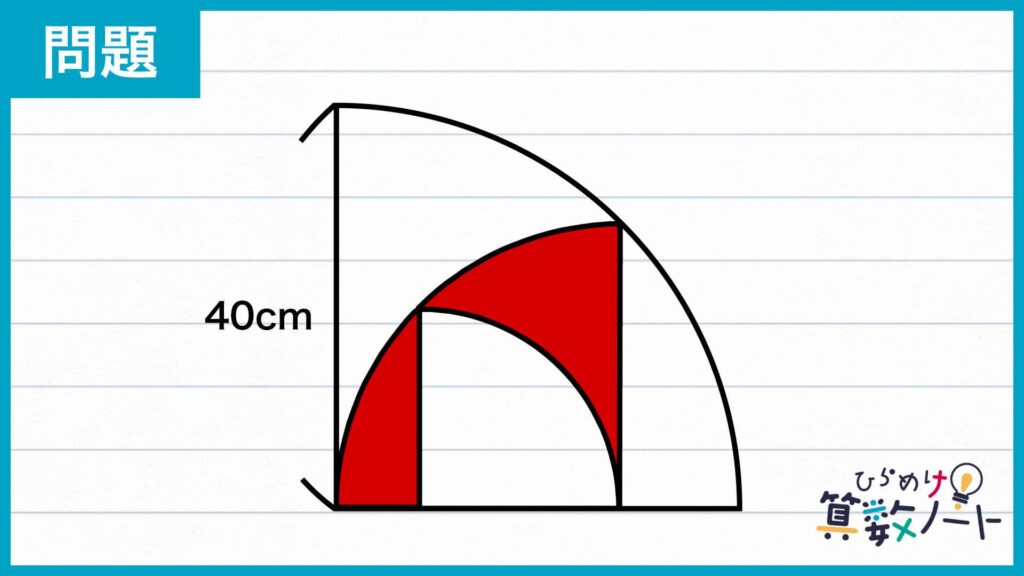
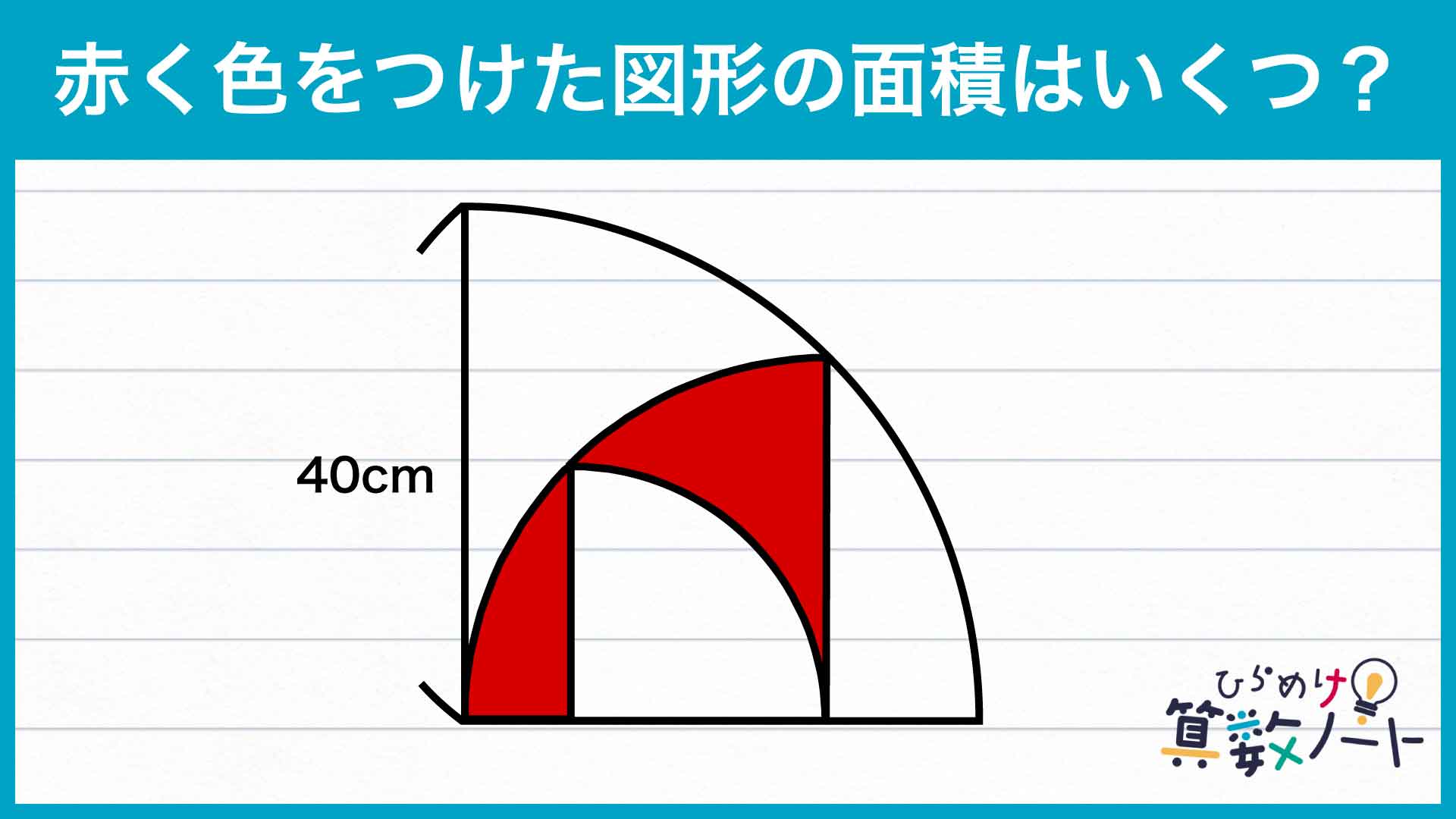
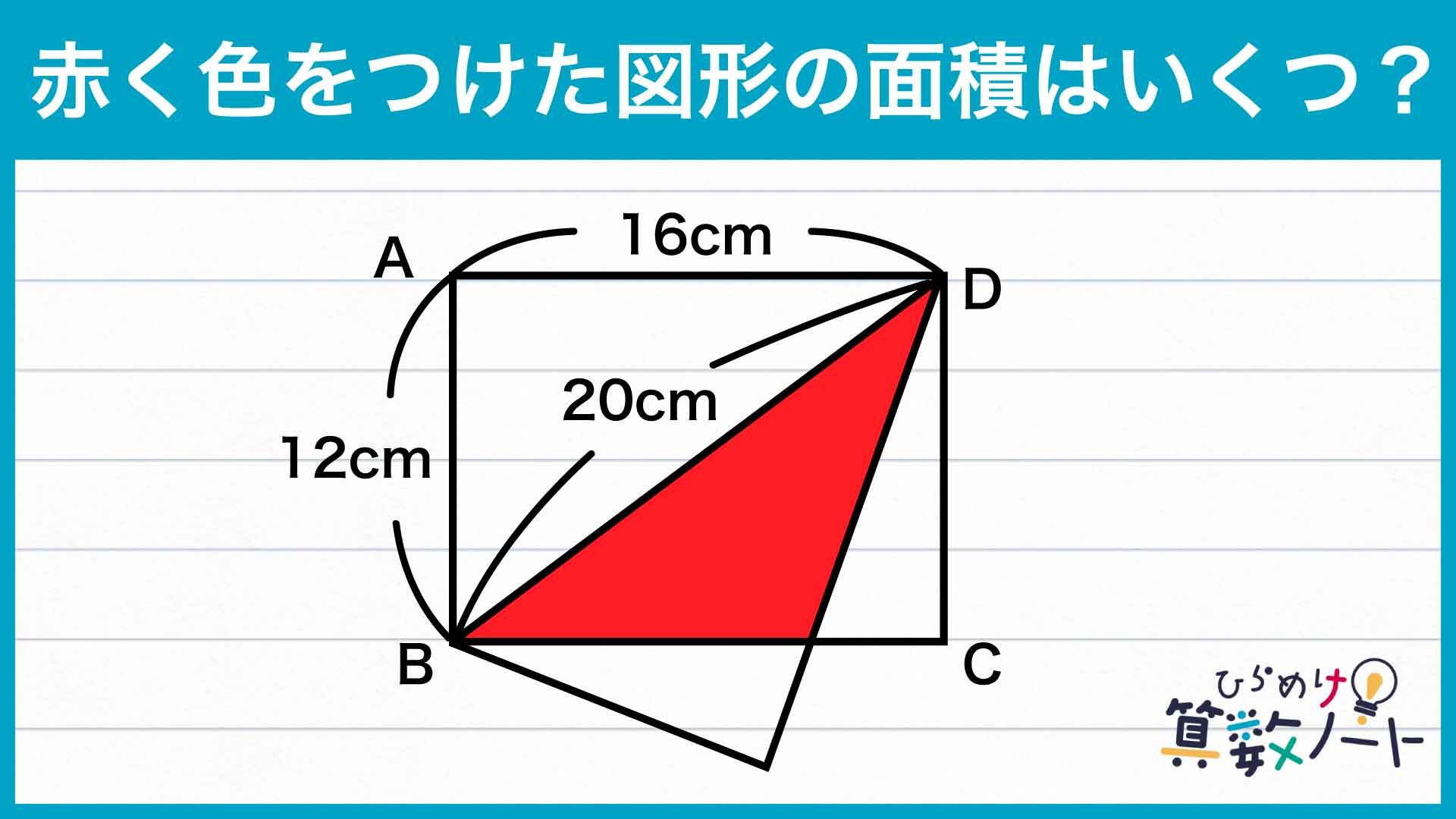
小学生でも解ける「扇形の重なり面積」に挑戦！あなたはひらめけますか？

問題はこちら

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

内側の扇形、半径を求めるのはかなり難しそうですが……？

この問題の解き方をまとめた図がこちらです。

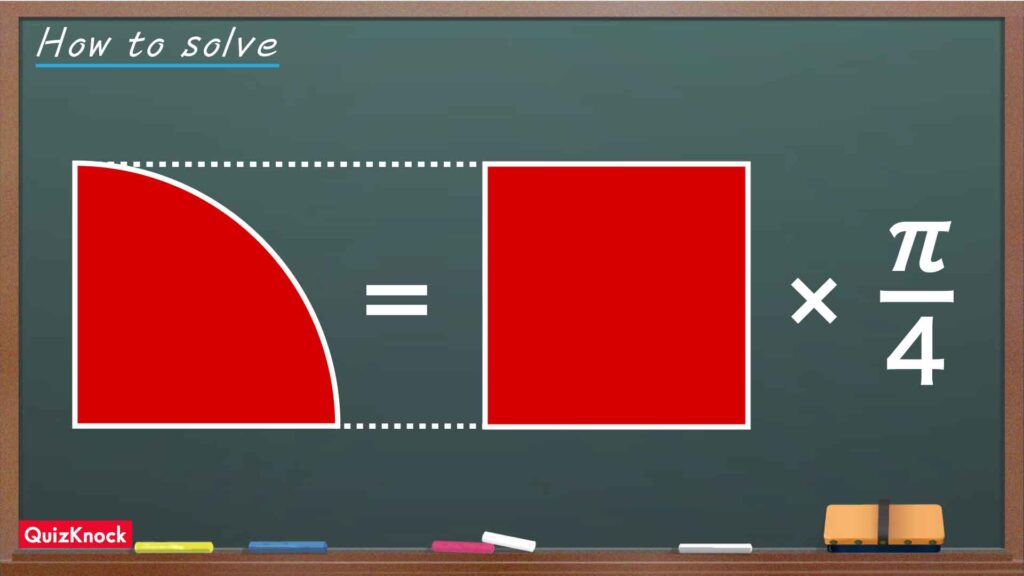
今回のポイントは「図形の中にある扇形と正方形のつながりに気づくこと」です。

このポイントをもとに、問題を攻略していきましょう！

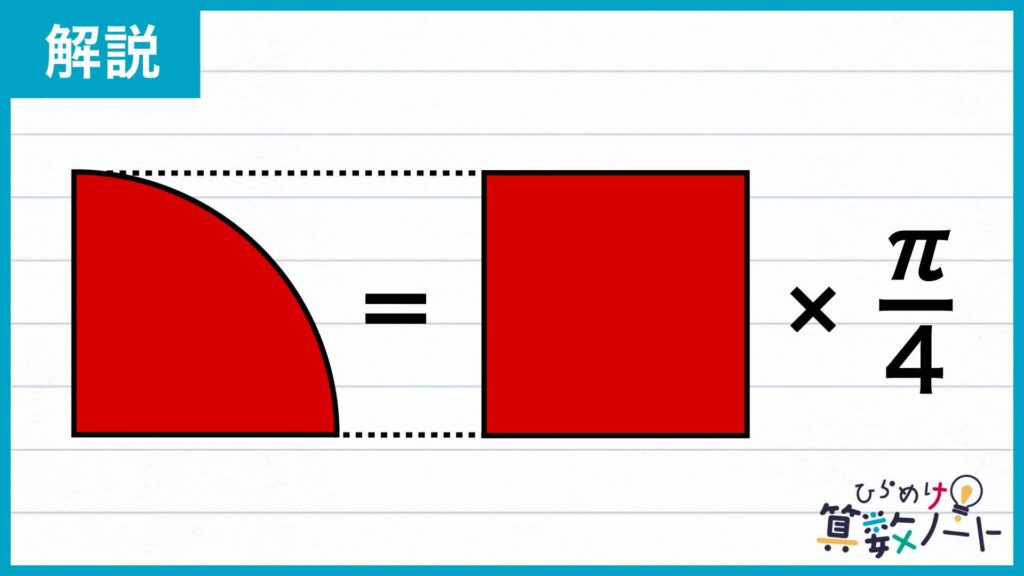
扇形の半径=正方形の一辺の長さ=▲とすると、

扇形の面積は▲×▲×π×1/4、正方形の面積は▲×▲なので扇形の面積=正方形の面積×π/4となることがわかります。

この性質を活かせば、半径をいちいち求めなくても扇形の面積が一気にわかっていきます。

まず、下の図のように点O、A、B、Cを置きます。

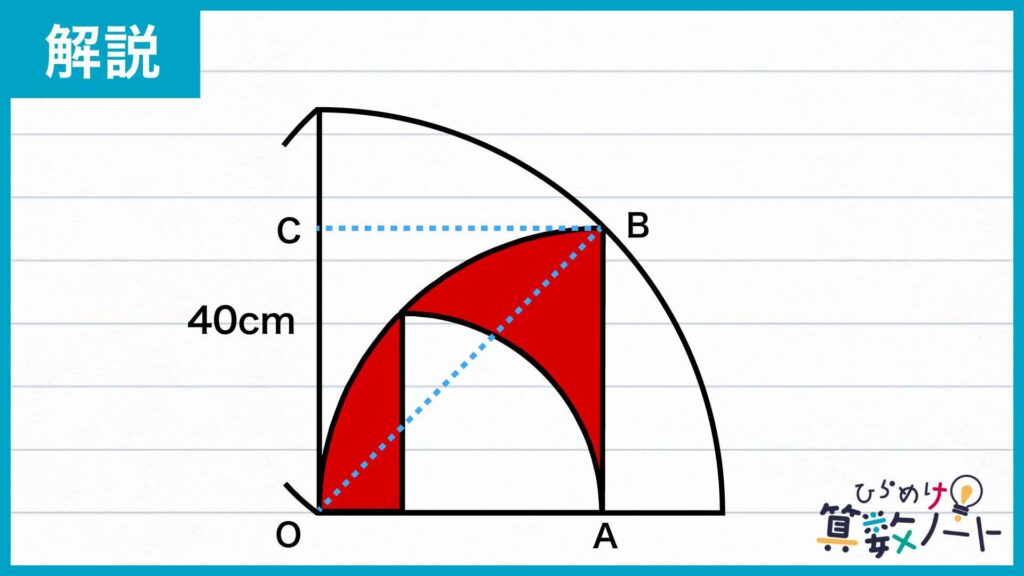
正方形OABCの対角線の長さは一番外側の扇形の半径と等しいので、正方形OABCの面積は40×40÷2=800cm²

扇形OABの面積=正方形OABCの面積×π/4なので、扇形OABの面積は800×π/4=200πcm²

続いて、下の図のように点D、E、Fを置きます。

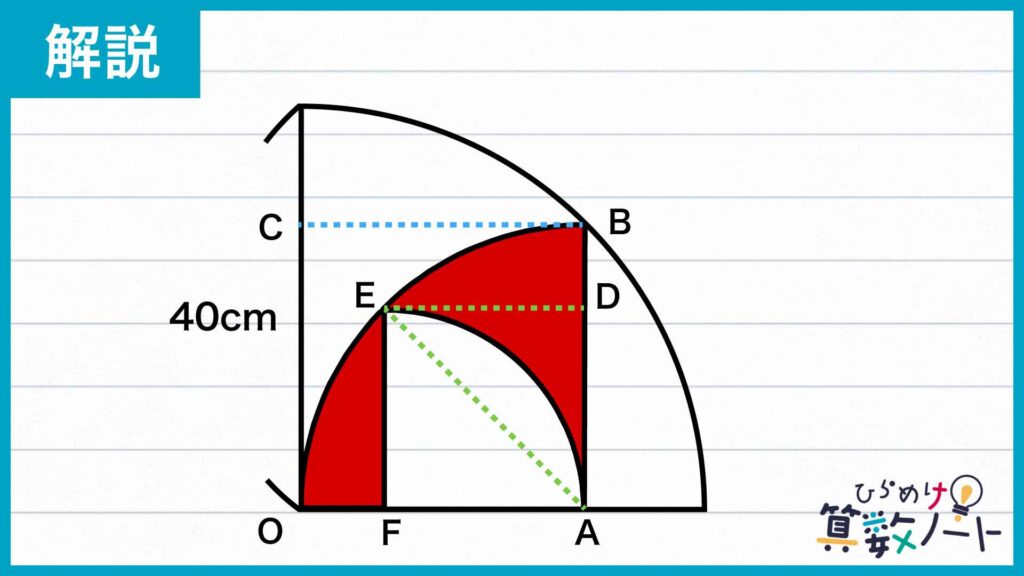
すると、正方形ADEFの対角線の長さは正方形OABCの一辺の長さと等しくなります。

正方形OABCの面積はAB×AB=800 cm²であり、ABの長さとAEの長さは等しいので、正方形ADEFの面積は800÷2=400cm²となります。

同様にして、扇形AEFの面積=正方形ADEFの面積×π/4なので、扇形AEFの面積は400×π/4=100πcm²

求める面積は、扇形OABの面積-扇形AEFの面積=200π-100π=100πcm²となります。

答え：100πcm²

正方形の面積をもとに扇形の面積が求められると気づけるかがカギでした！

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】