問題はこちら
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
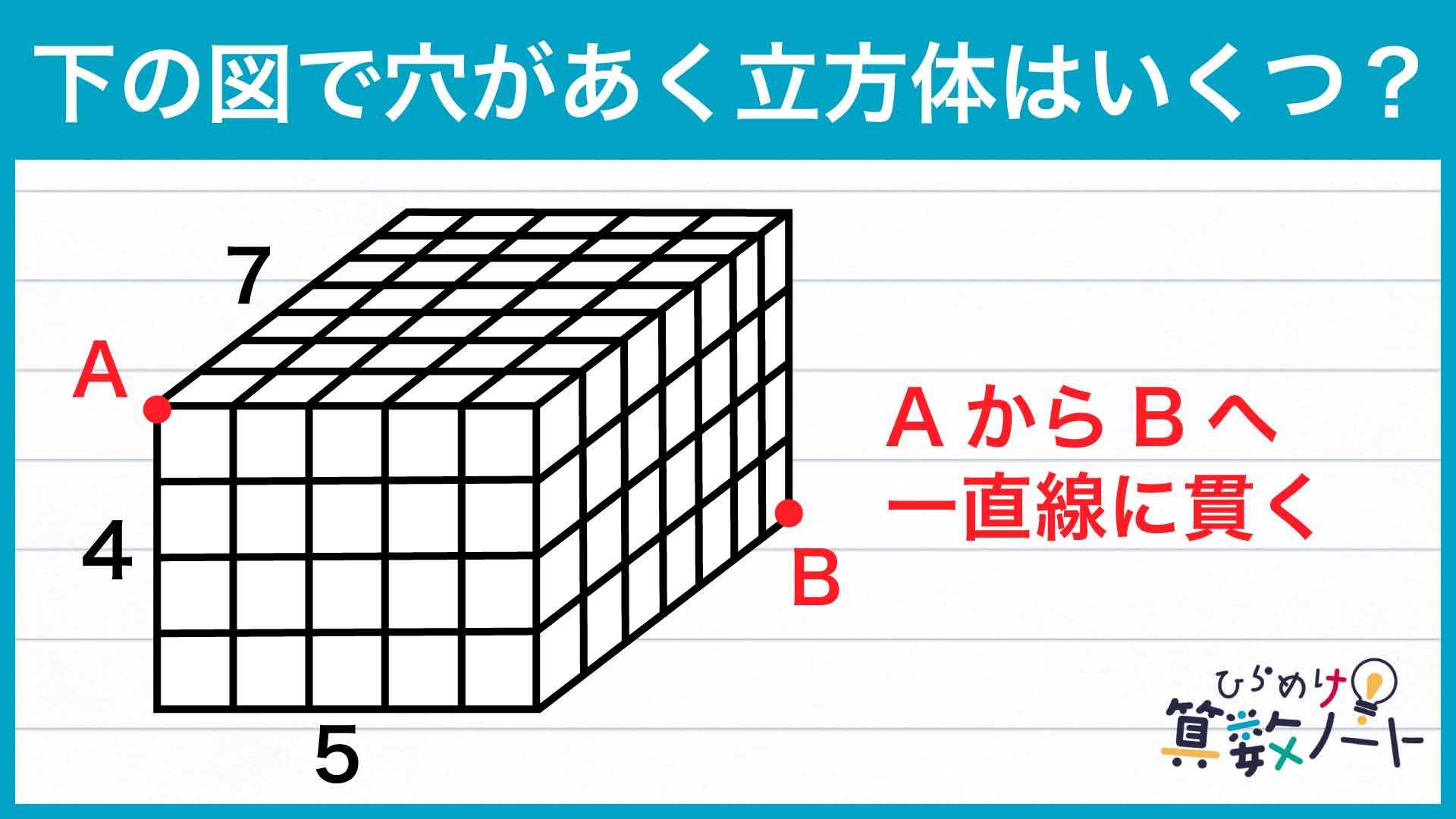
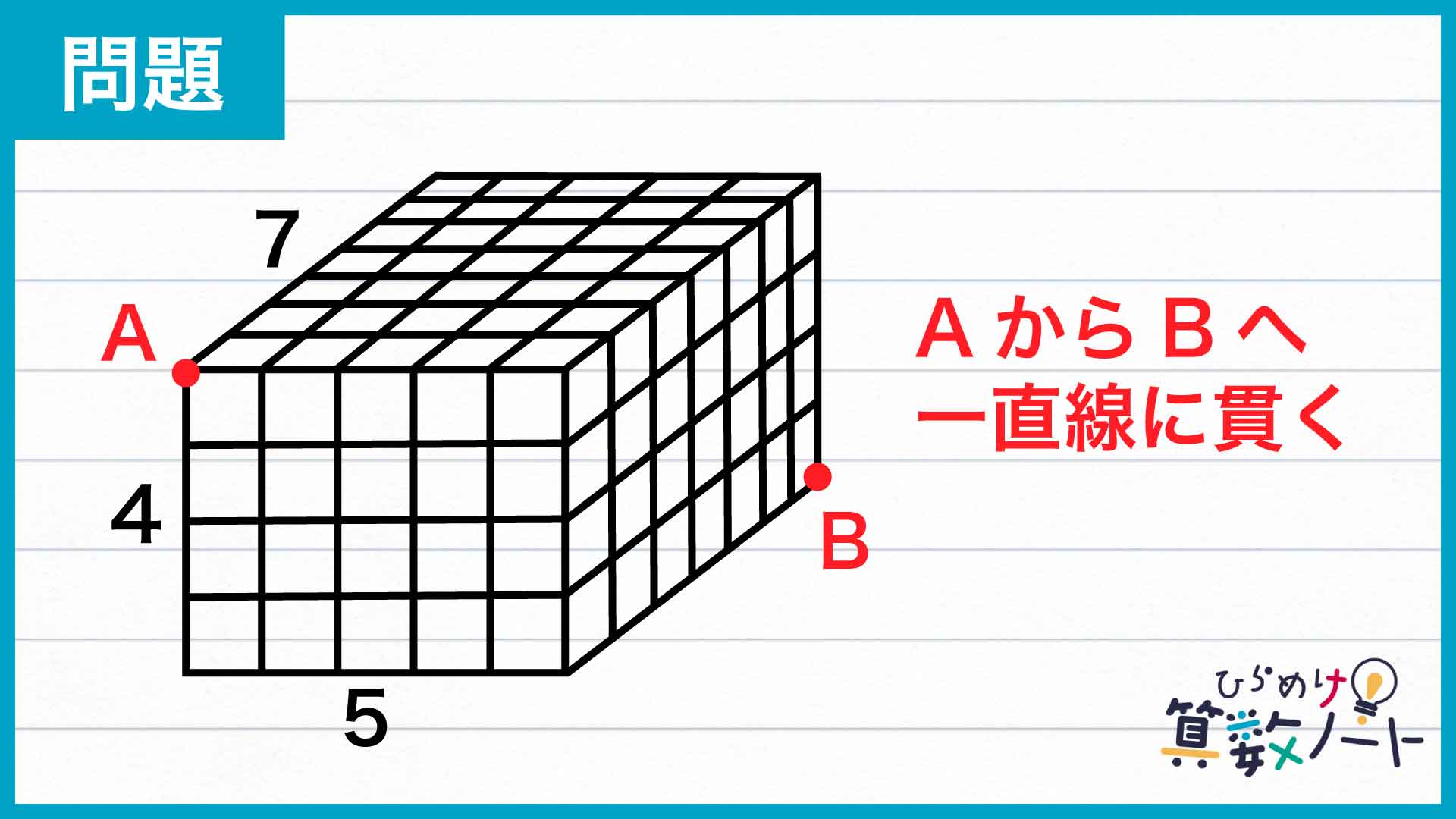
この問題の解き方をまとめた図がこちらです。
大切なのは、点Aから点Bへ行くまでに「破る面の数」を意識することです。
では、このポイントを踏まえつつ解いていきましょう!
解説はこちら
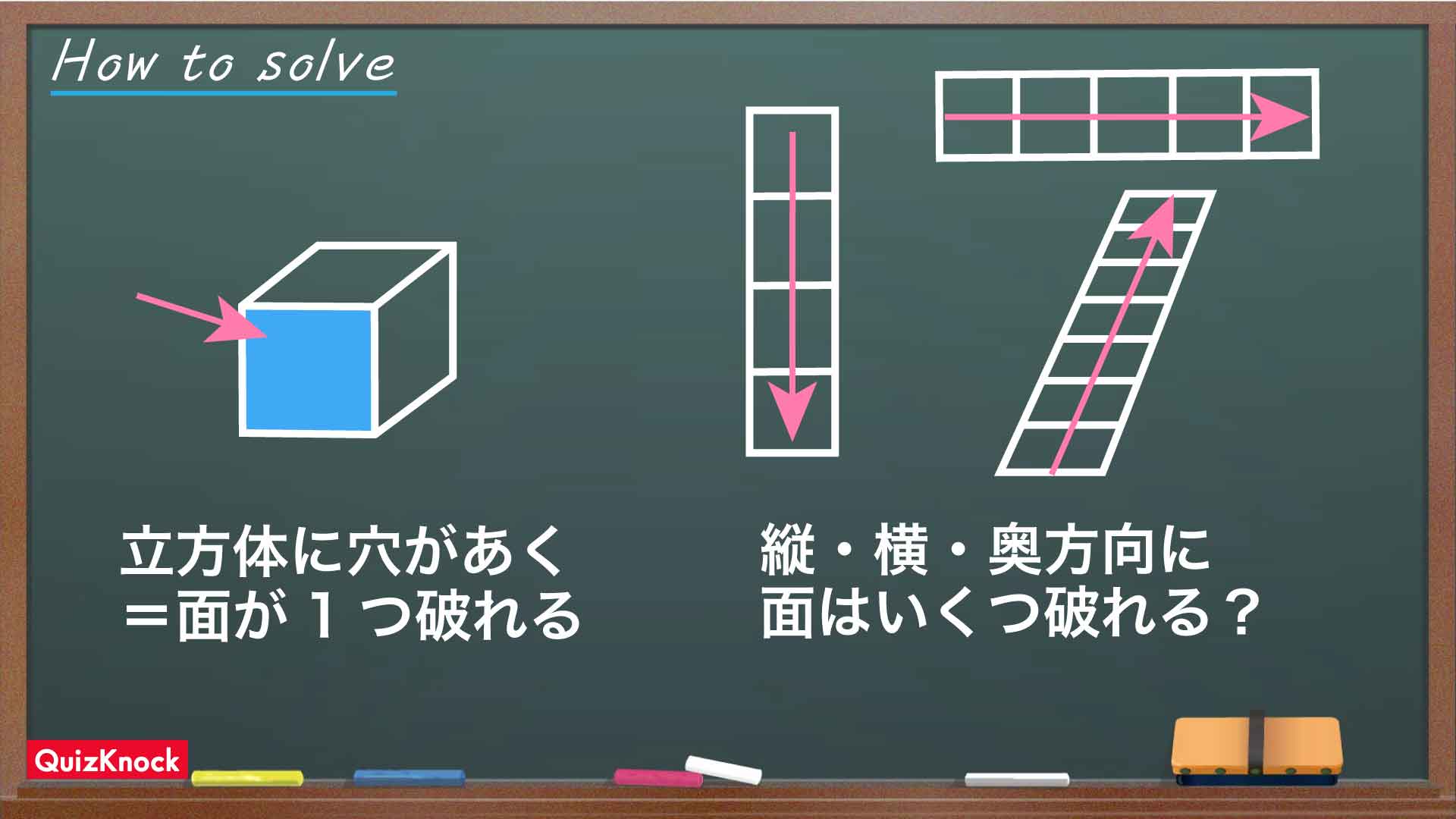
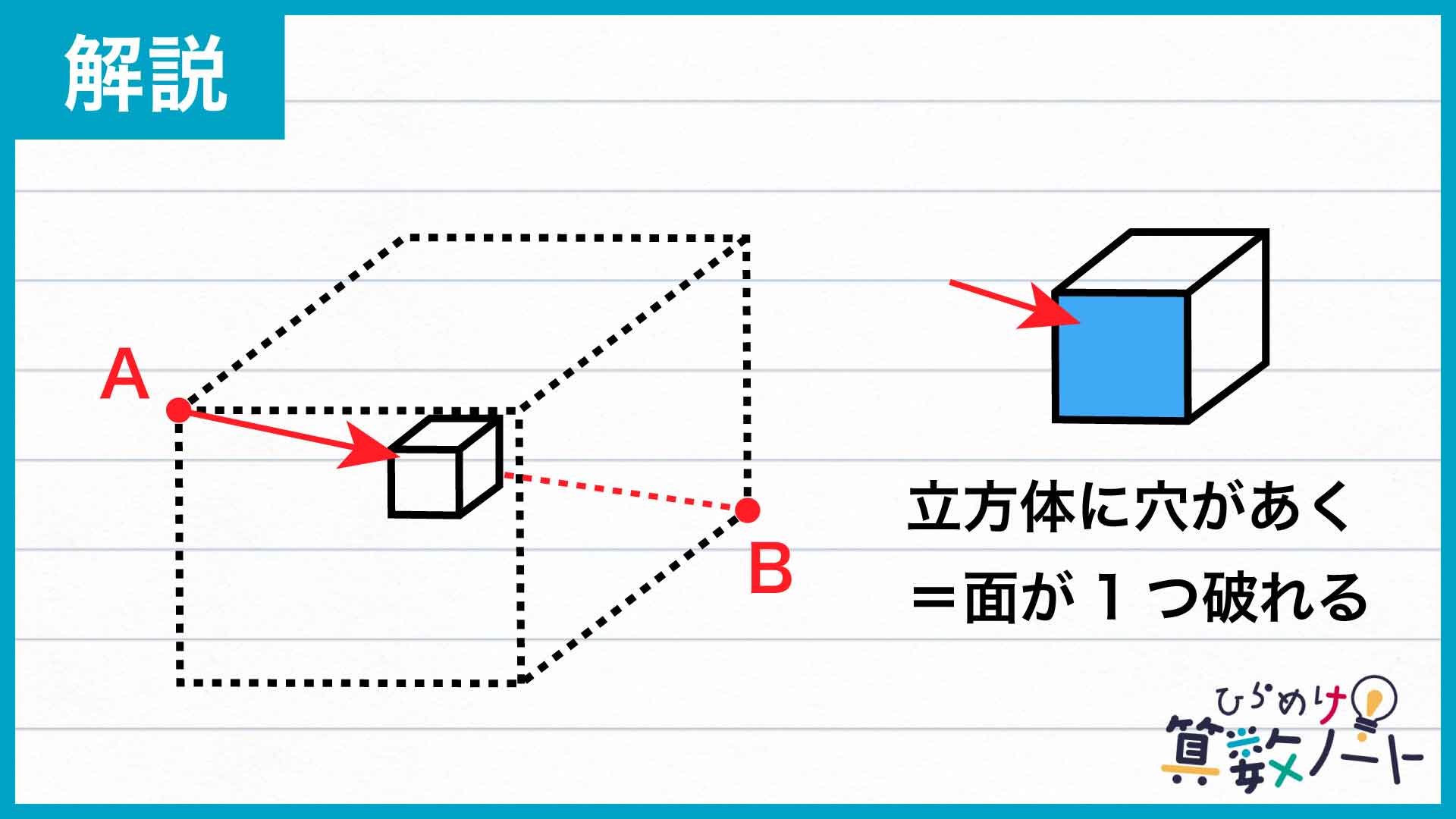
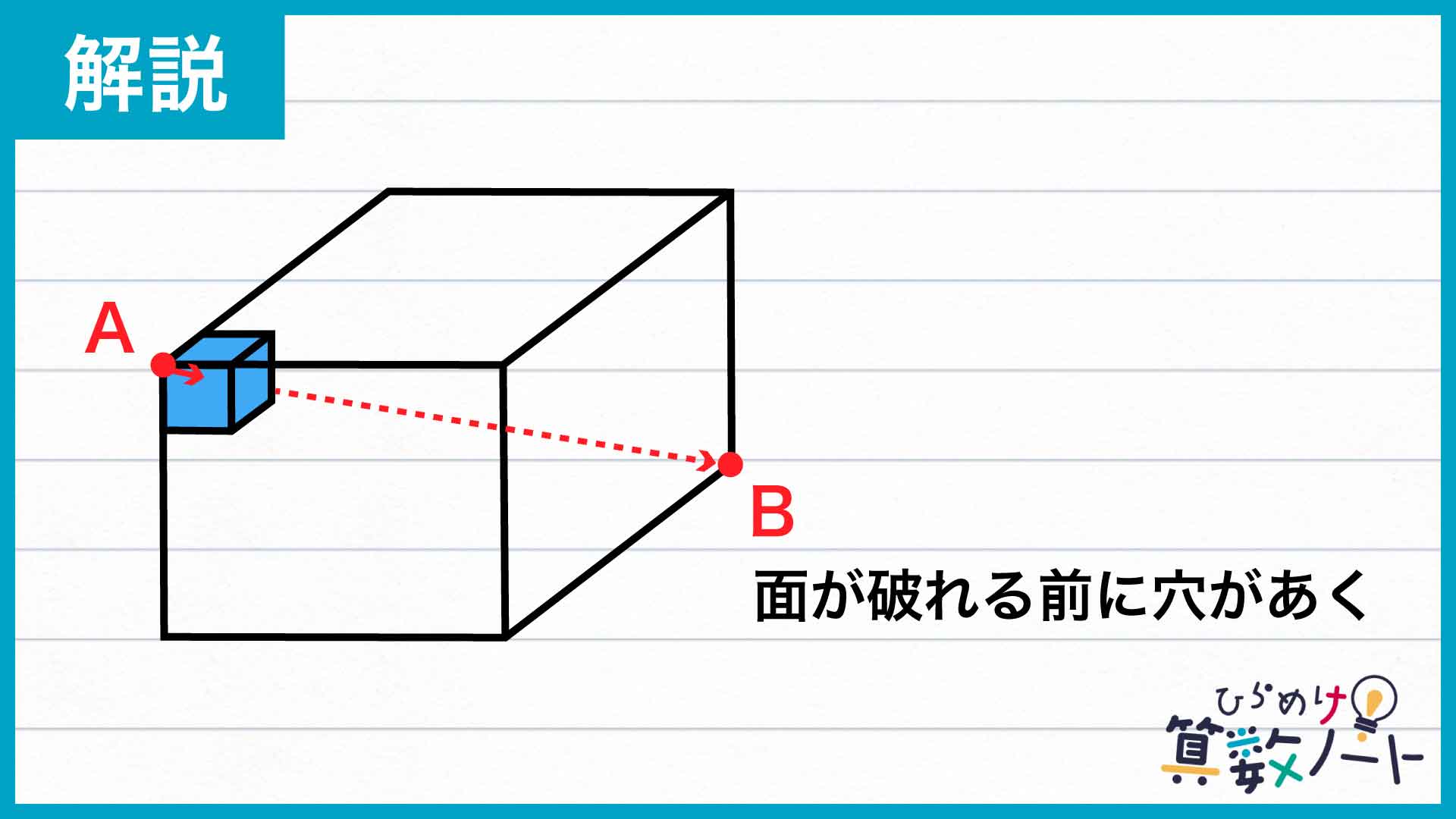
「立方体に穴があく」という現象を別の視点からとらえ直してみましょう。たとえば、下の図のような1×1×1の立方体の手前の面にぶつかったとします。この立方体に新しく穴があくのは、手前の面が貫かれたときです。そしてこの立方体の異なる面を破って外に出ると、隣り合った立方体にまた新しく穴があきます。
つまり、「立方体に新しく穴があく」という現象は、「立方体のある面が新しく破れる」という現象と1対1対応になっているのです。
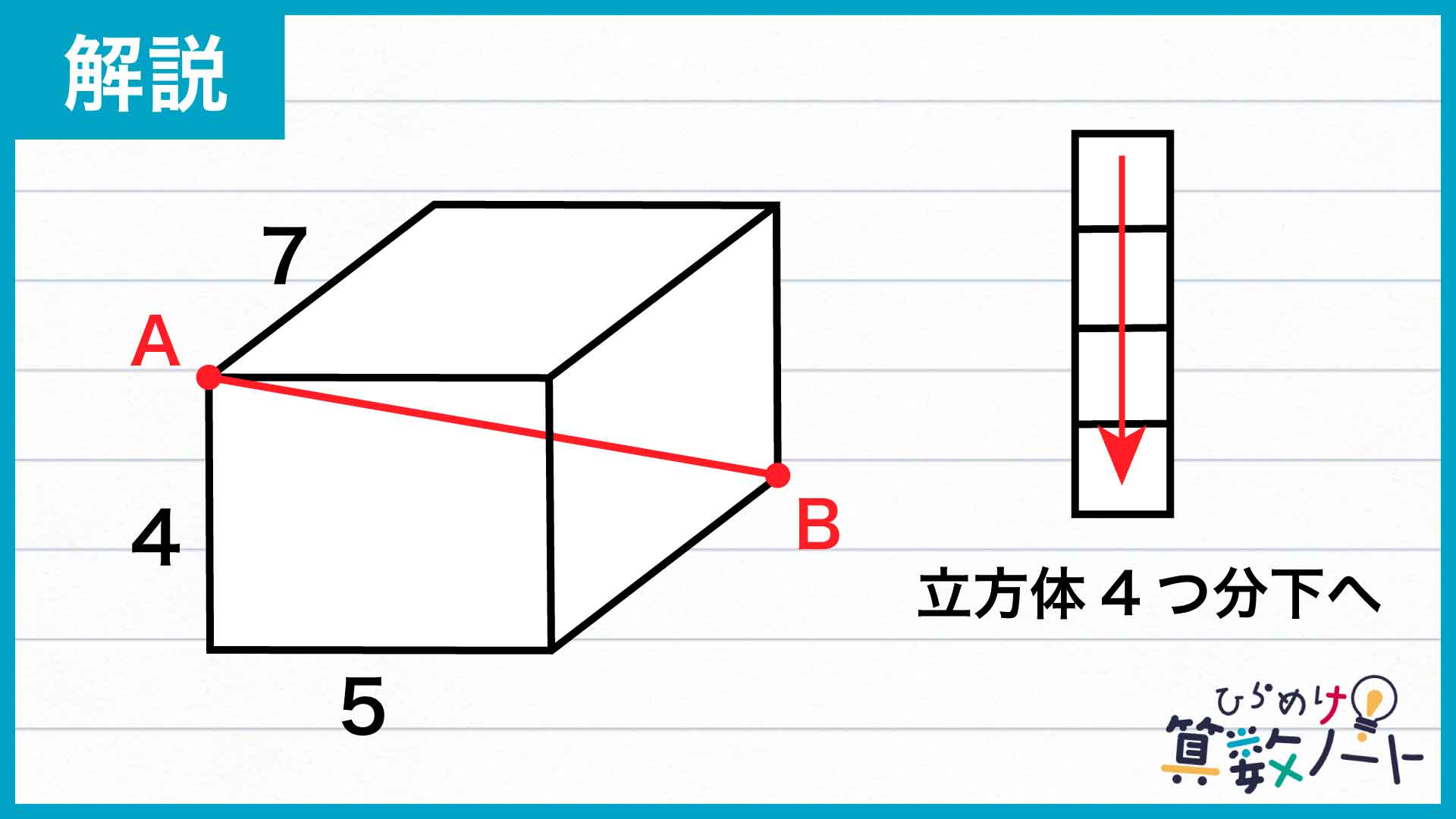
そして、点Aから点Bへ移動するには、縦・横・奥行きそれぞれの方向に面を破っていく必要があります。たとえば、縦方向へは立方体4つ分だけ下る必要があり、このとき「面が破れる」回数は合計3回です。
横、奥行きの方向についても同じように考えます。それぞれの方向へ移動するときに「面が破れる」回数は、5-1=4回と7-1=6回です。それぞれの面が破れるごとに新しい立方体に穴があきます。そして、忘れてはいけないのが点Aを含んでおり一番最初に穴があく立方体。この立方体だけは、「面が破れる」現象とは別に穴があくので追加でカウントしなくてはなりません。
したがって、求める立方体の個数の合計は3+4+6+1=14個となるのです。
答え:14個
おまけ
実はこの問題には、1つ注意点があります。それは、場合によっては「立方体1つに穴があくとき複数の面が破れる」ことがあるという点です。
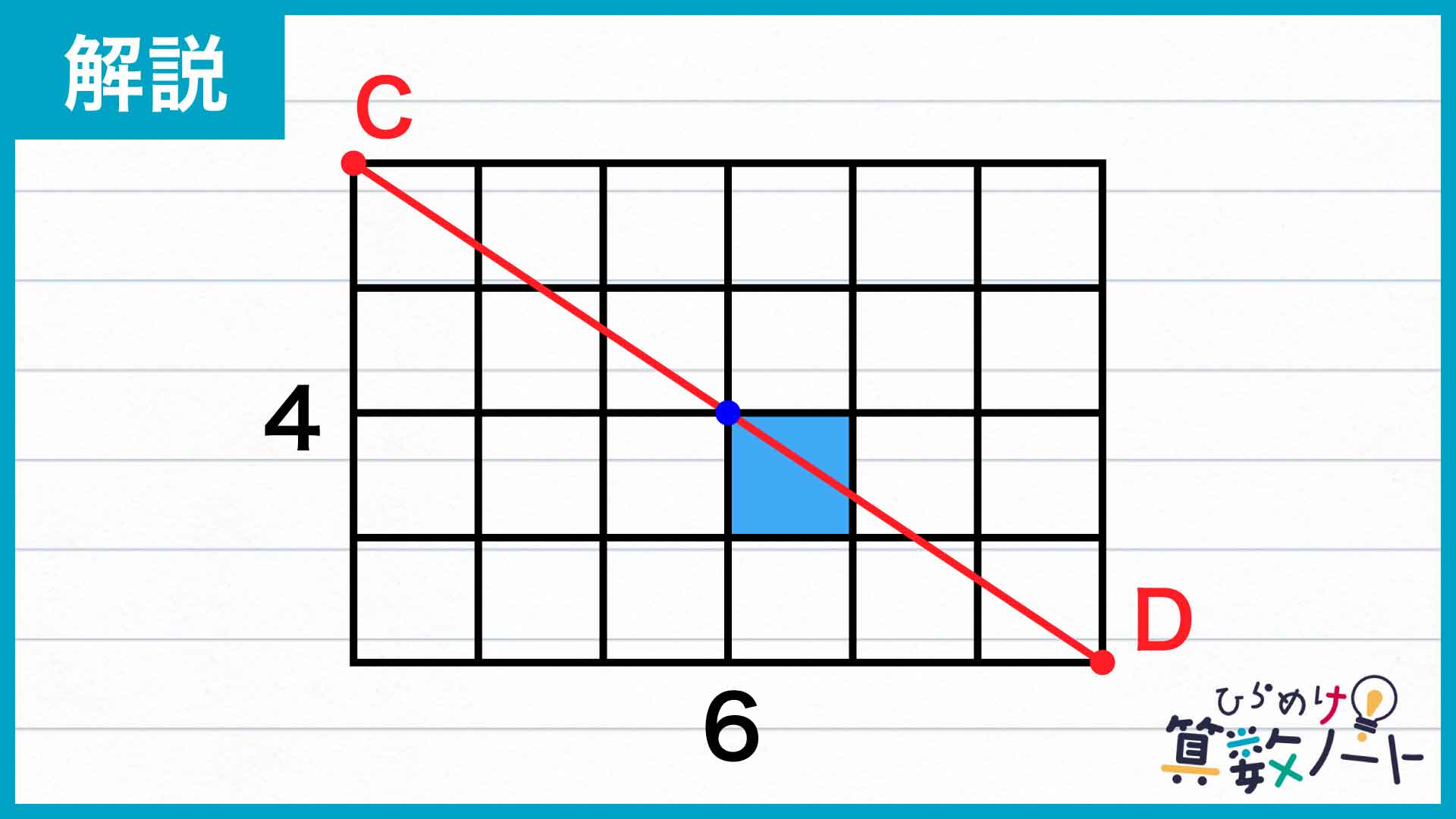
状況を簡単にするため、下の図のように平面的な4×6の長方形の点Cから点Dへ動くことを考えてみましょう。
このとき、青い点の部分に注目します。ここでは他の部分と異なり、新しい正方形の中へ入る際に縦・横の境の面が同時に破れていることになります。つまり、「新しく穴があく」ということと「面が1つ破れる」ということが1対1対応ではなくなってしまうのです。
このような状況は、全体の辺の長さ同士が1以外の公約数を持つ(=互いに素ではない)場合に発生します。今回扱った4×5×7の直方体では辺の長さが互いに素であるため、このような場合を考える必要はなかったのです。
「ひらめけ!算数ノート」のバックナンバーはこちら!。
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)










.jpg)







