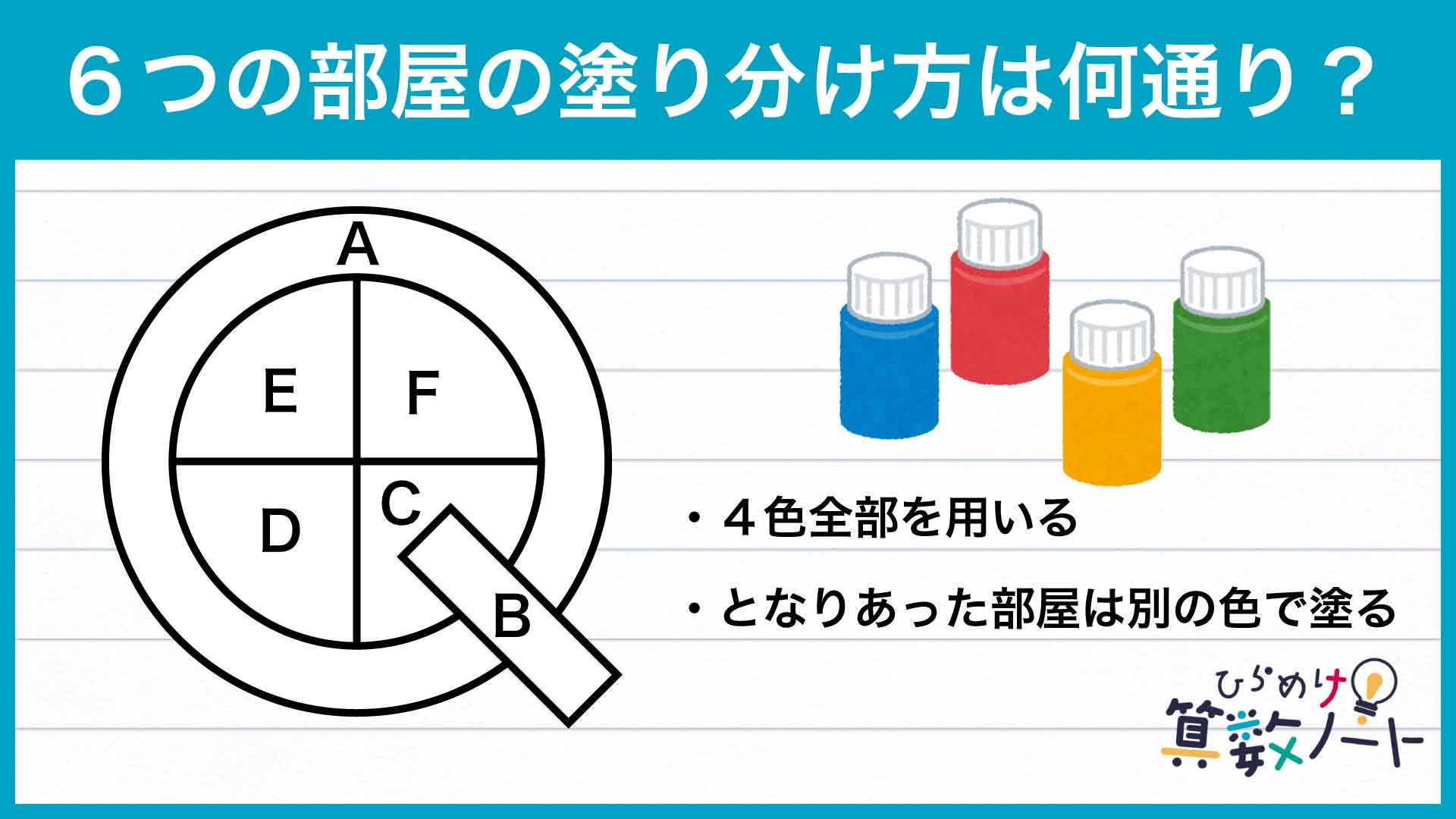
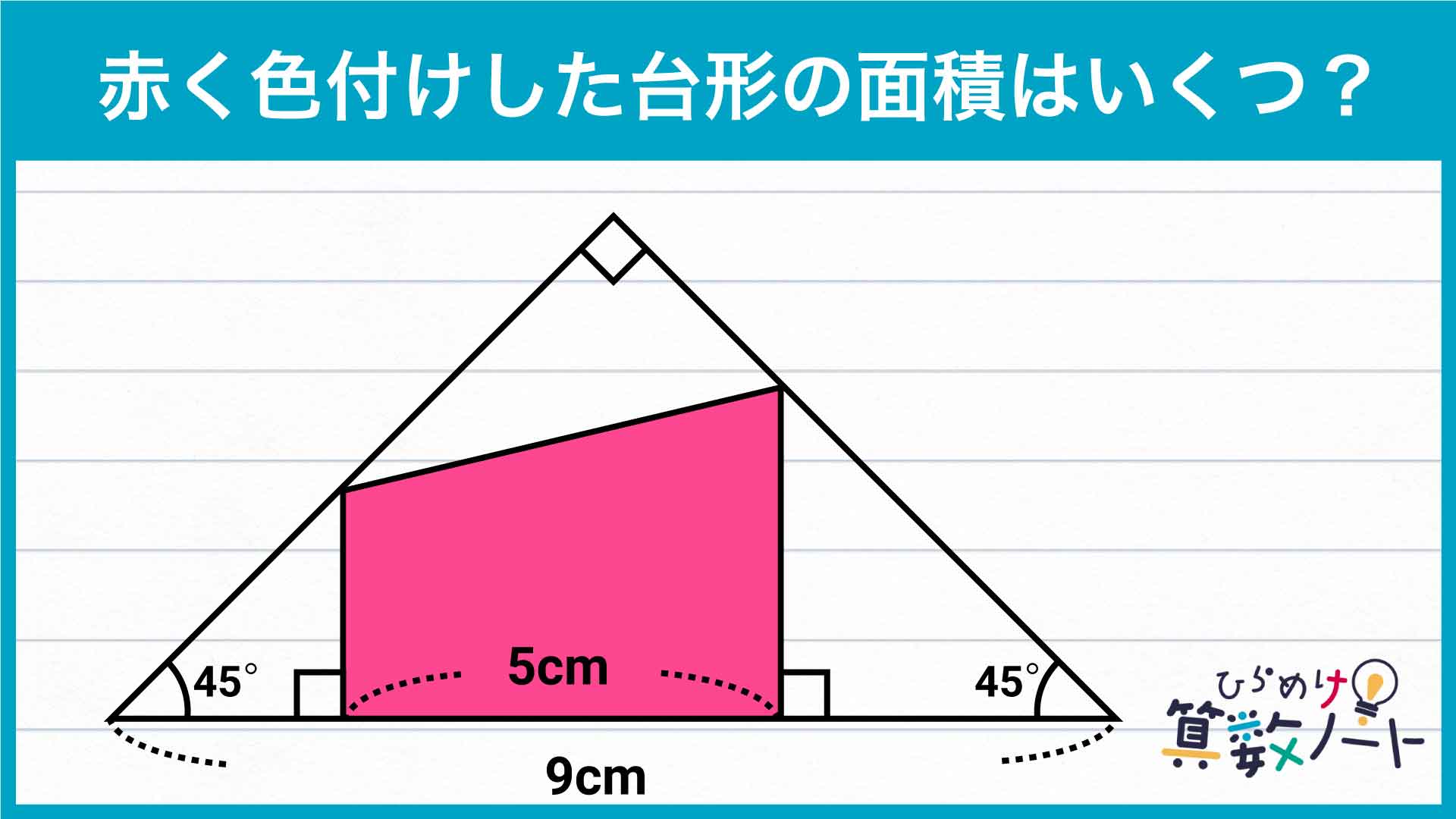
問題はこちら
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
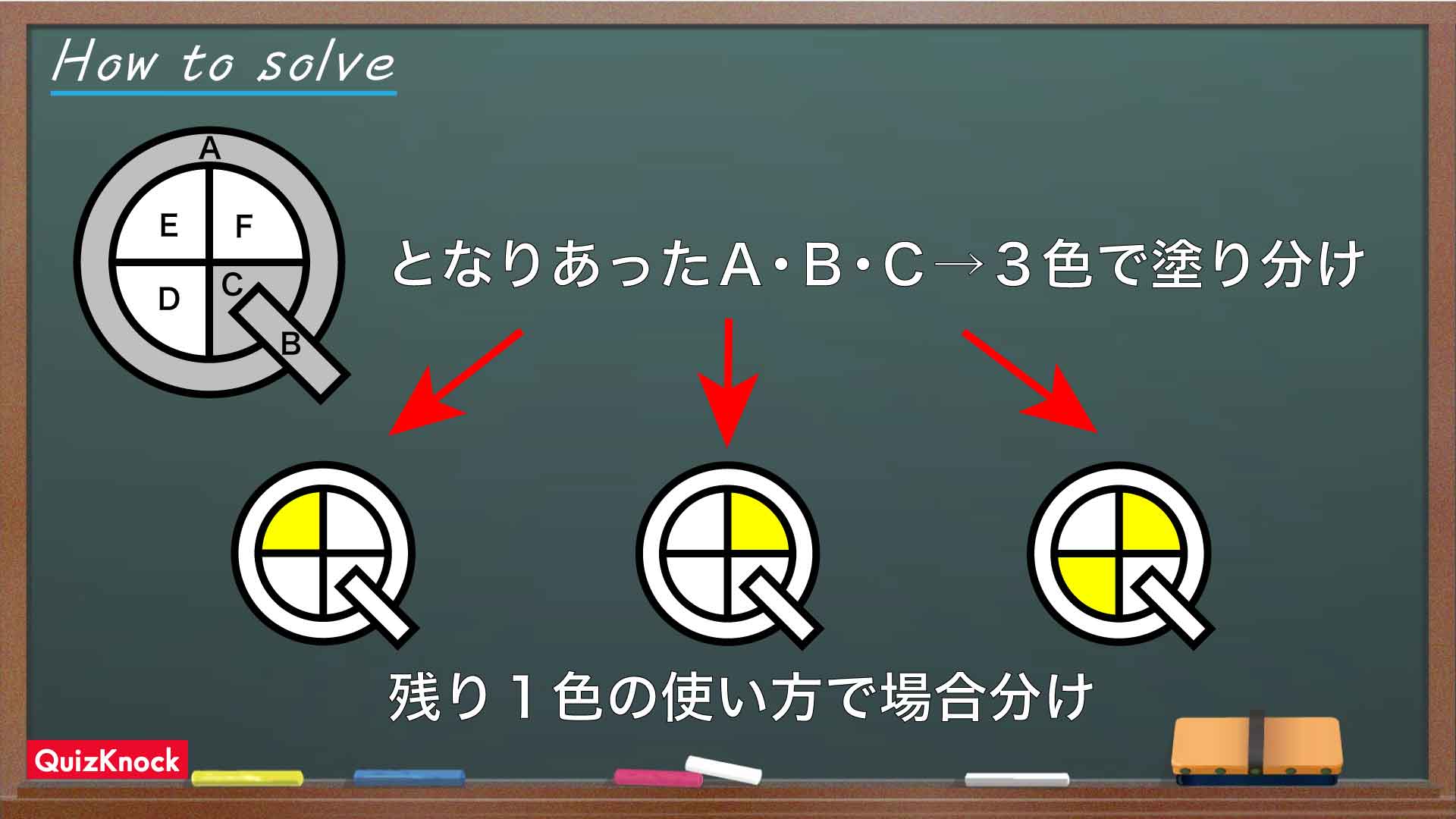
この問題の解き方をまとめた図がこちらです。
ポイントは、考える部屋の数を絞ってから丁寧に場合分けをすることです。
では、このポイントを踏まえつつ解いていきましょう!
塗り方が限られたエリアを考える
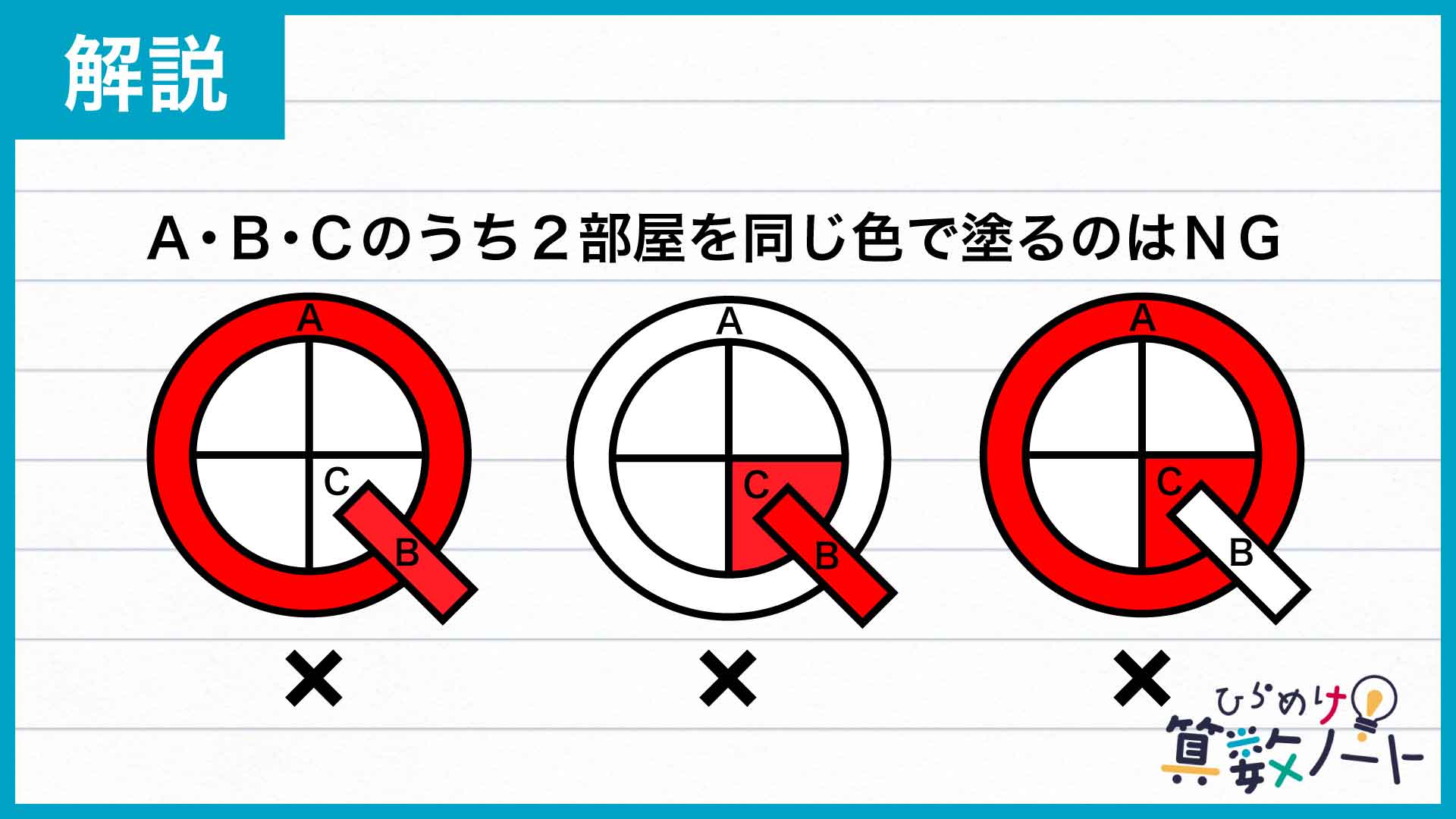
6部屋の塗り方をいっぺんに考えるのは大変です。まずは、A・B・Cの部屋のみに注目してみましょう。これら3部屋をよく見るとそれぞれとなりあっており、どの2部屋の組み合わせでも同じ色で塗ることはできません。
したがって、A・B・Cを塗り分けるには4色あるペンキのうち必ず3色を使わなければならないということになります。
言い換えれば、残る1色の使い方を考えるだけで部屋の塗り分けパターンを全て考えたことになるのです。
残り1色の使い方を考える
「4色のペンキを全て用いる」という条件から、A・B・Cに使っていない1色についてもD・E・Fのうち少なくとも1部屋を塗るのに使わなければなりません。
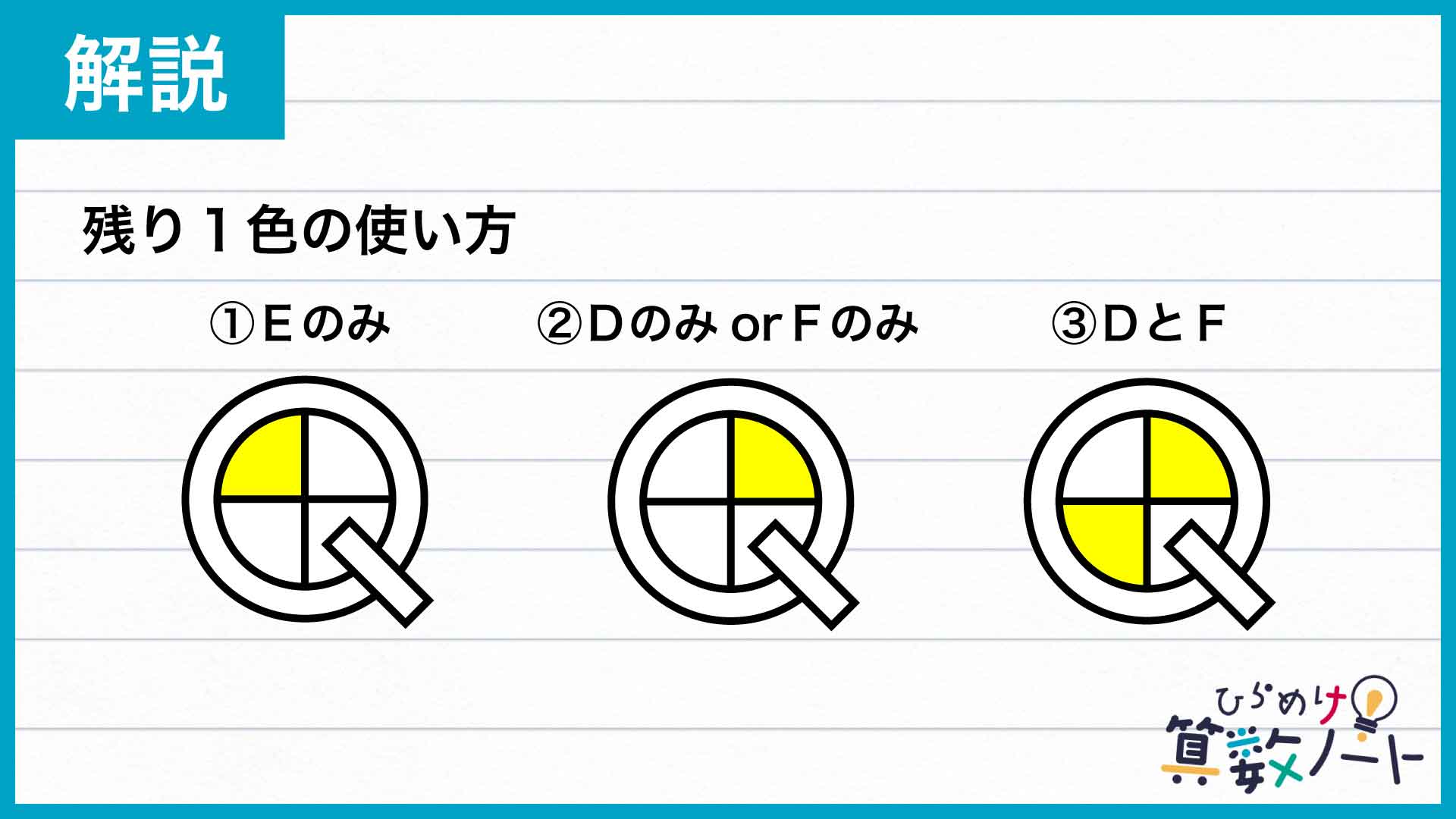
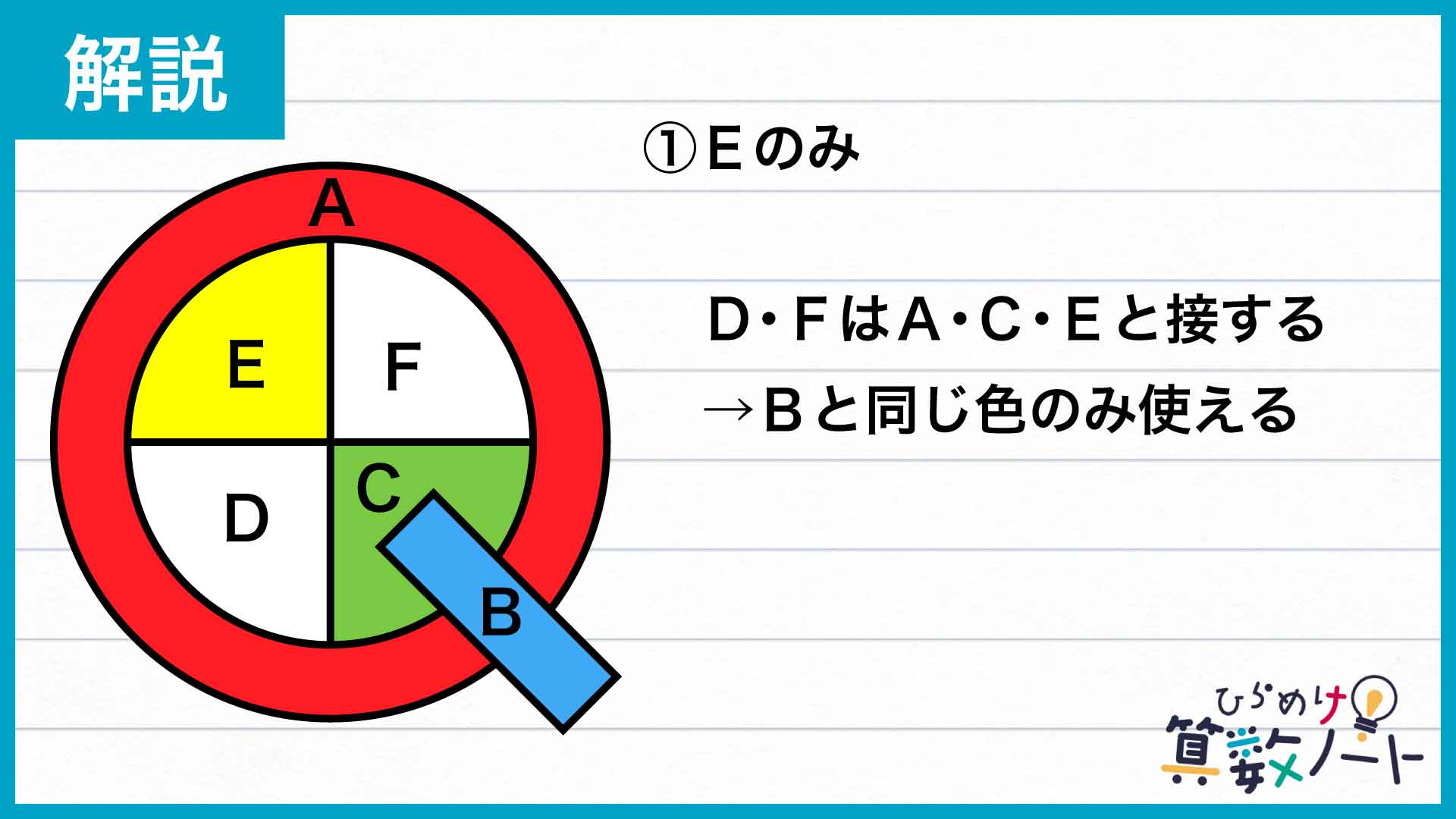
Eの部屋が他2部屋と接していることに注意すると、残り1色の使い方はこちらの3パターンに分類できることがわかります。
①のパターンでは、A・C・Eにそれぞれ別の色が使われているため、DとFはこの3色以外の色、すなわちBと同じ色で塗るしかありません。
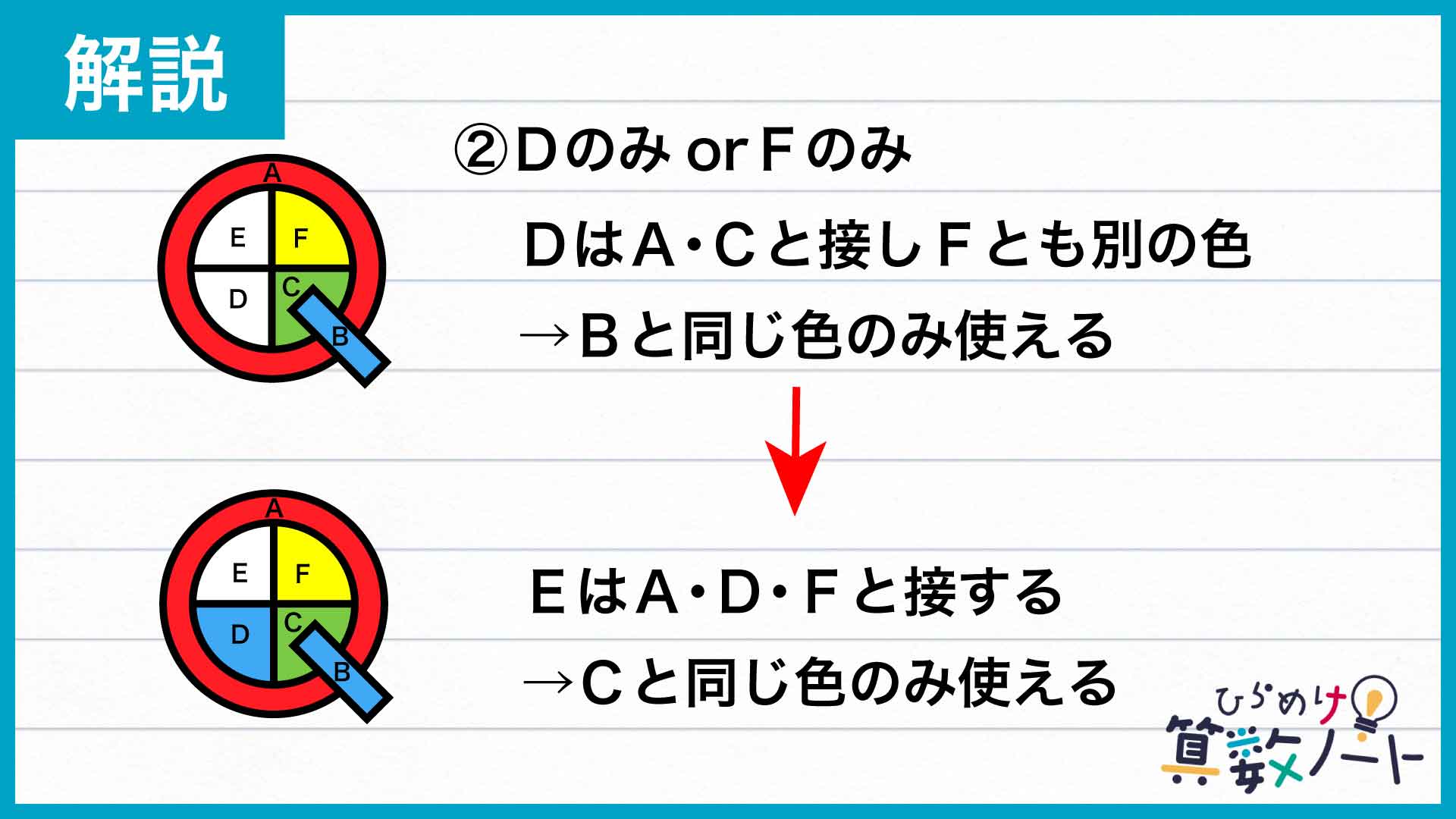
②でFに残りの1色を用いた場合、Dはとなり合うA・Cに加えてFとも違う色を用いる必要があるため、やはりBと同じ色で塗ることになります。このときEはというと、接するA・D・Fが異なる3色で塗られるため、Cと同じ色しか使うことができません。
Dに残り1色を用いた場合も同じです。よって、DまたはFの一方に残り1色を用いる場合の塗り分け方は、D・Fそれぞれ1パターンずつ、合計2パターンあることがわかります。
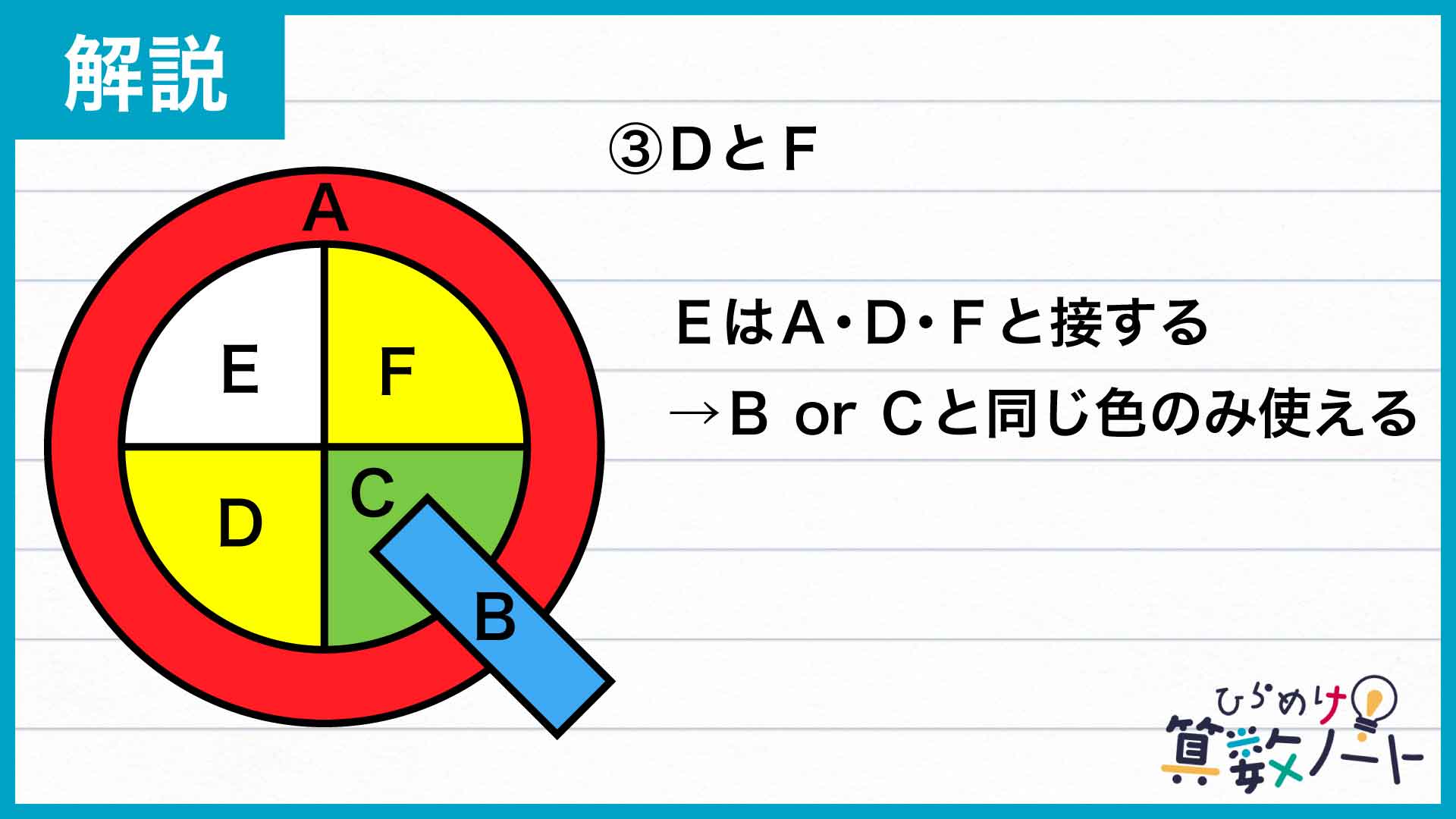
最後に③です。D・F両方に残り1色を使ったとき、Eに接するA・D・Fは2色のみで塗り分けられることになります。そのためEはBに使った色、Cに使った色のどちらで塗っても良いことになり、塗り分けのパターンは2つ存在します。
①〜③の場合を全て考えた結果、4色しかないペンキで6部屋を塗り分けるときのパターンは合計1+2+2=5つあることがわかりました。
最後に、塗り分けの各パターンにおいて4色あるペンキのうちどの色をどの部屋に使うかについても考える必要があるのです。
Aに使えるのは4色、Bに使えるのはAで使った以外の3色……というように考えていくと、1つの塗り分けパターンにつき実際の塗り分け方は4×3×2×1=24通りあることがわかります。
したがって、6部屋の塗り分け方は合計24×5=120通り存在します。
答え:120通り
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】