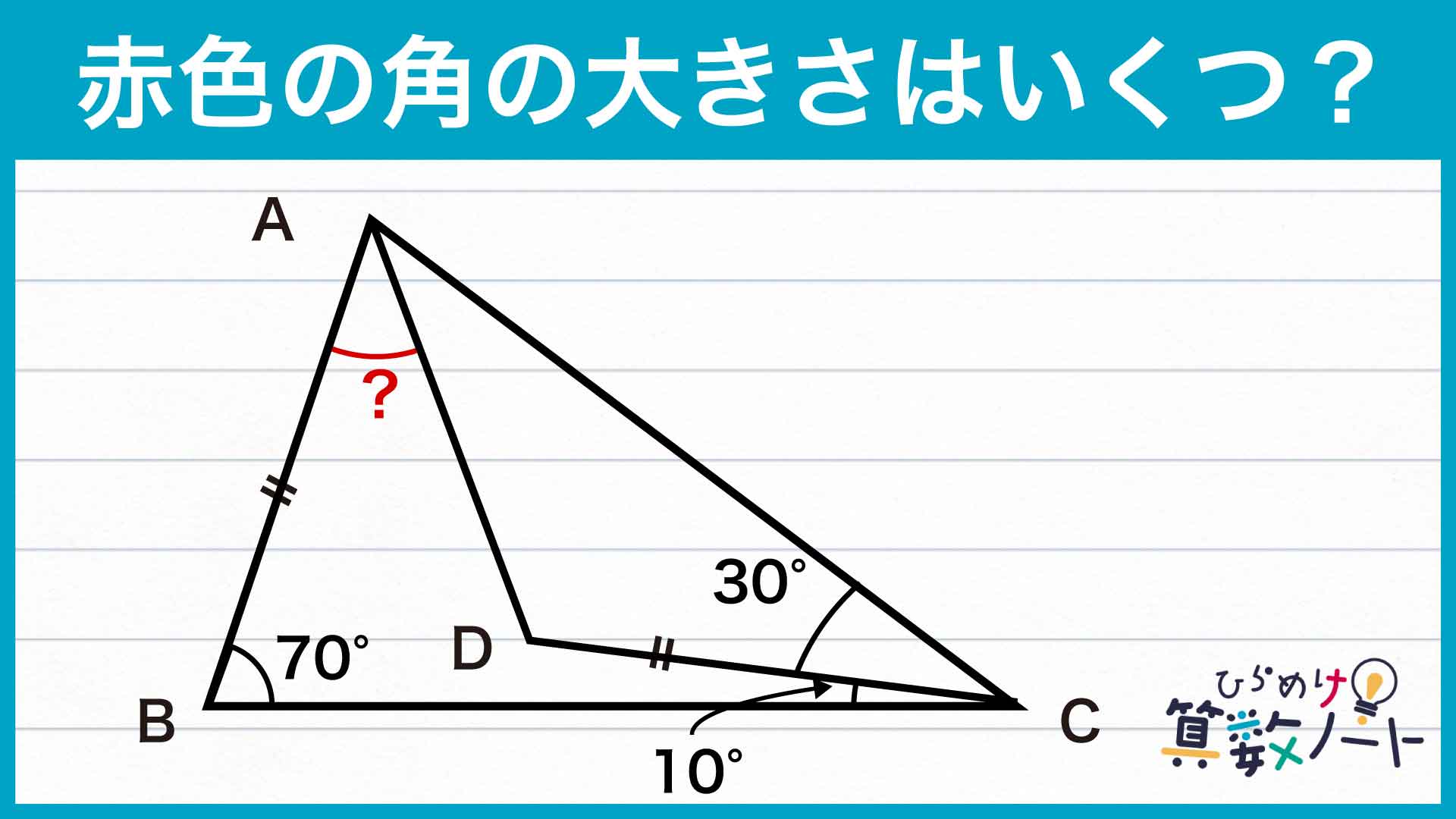
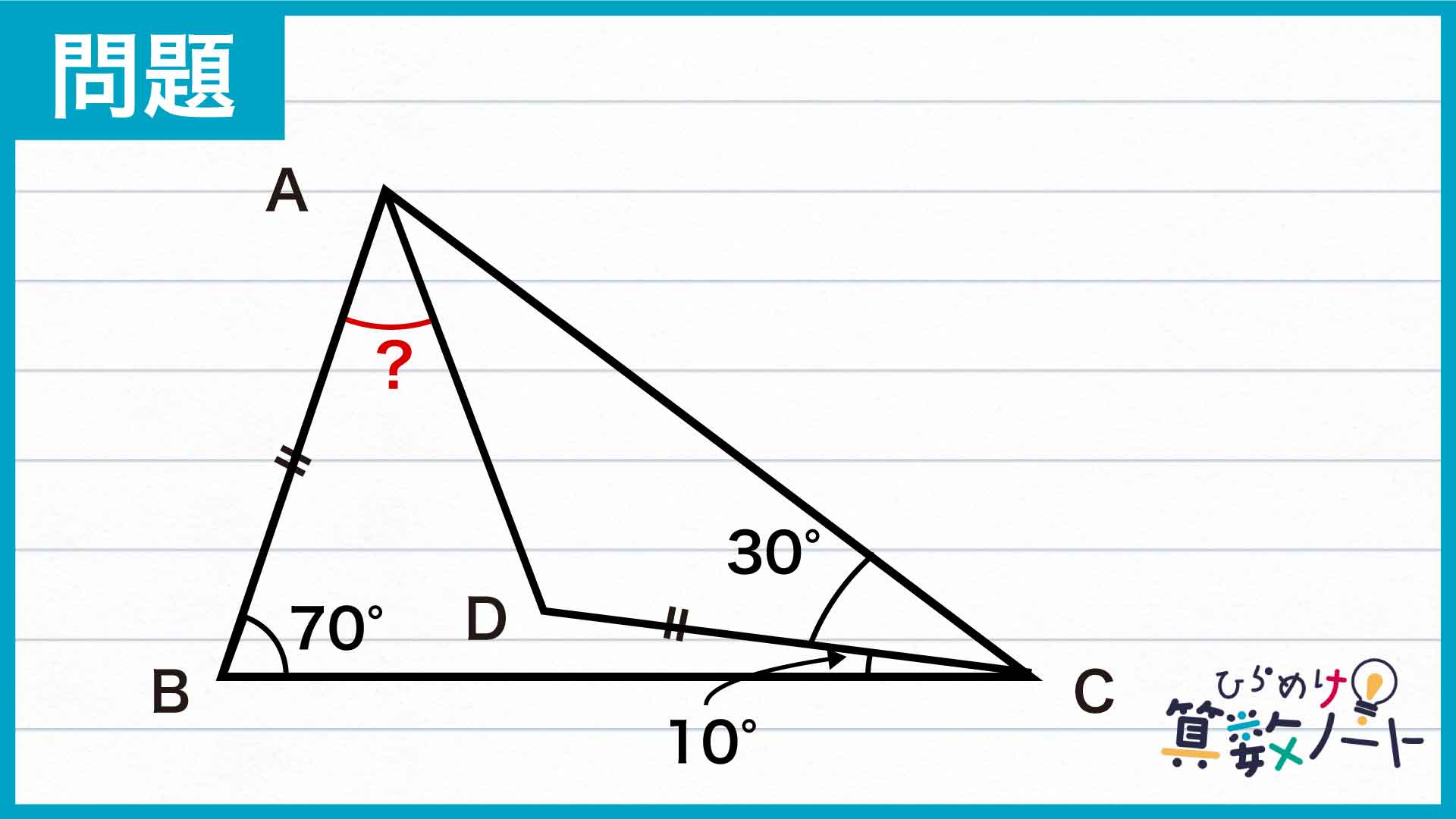
【問題はこちら】
1ページ目:自力で解きたい方はこちらへ!以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
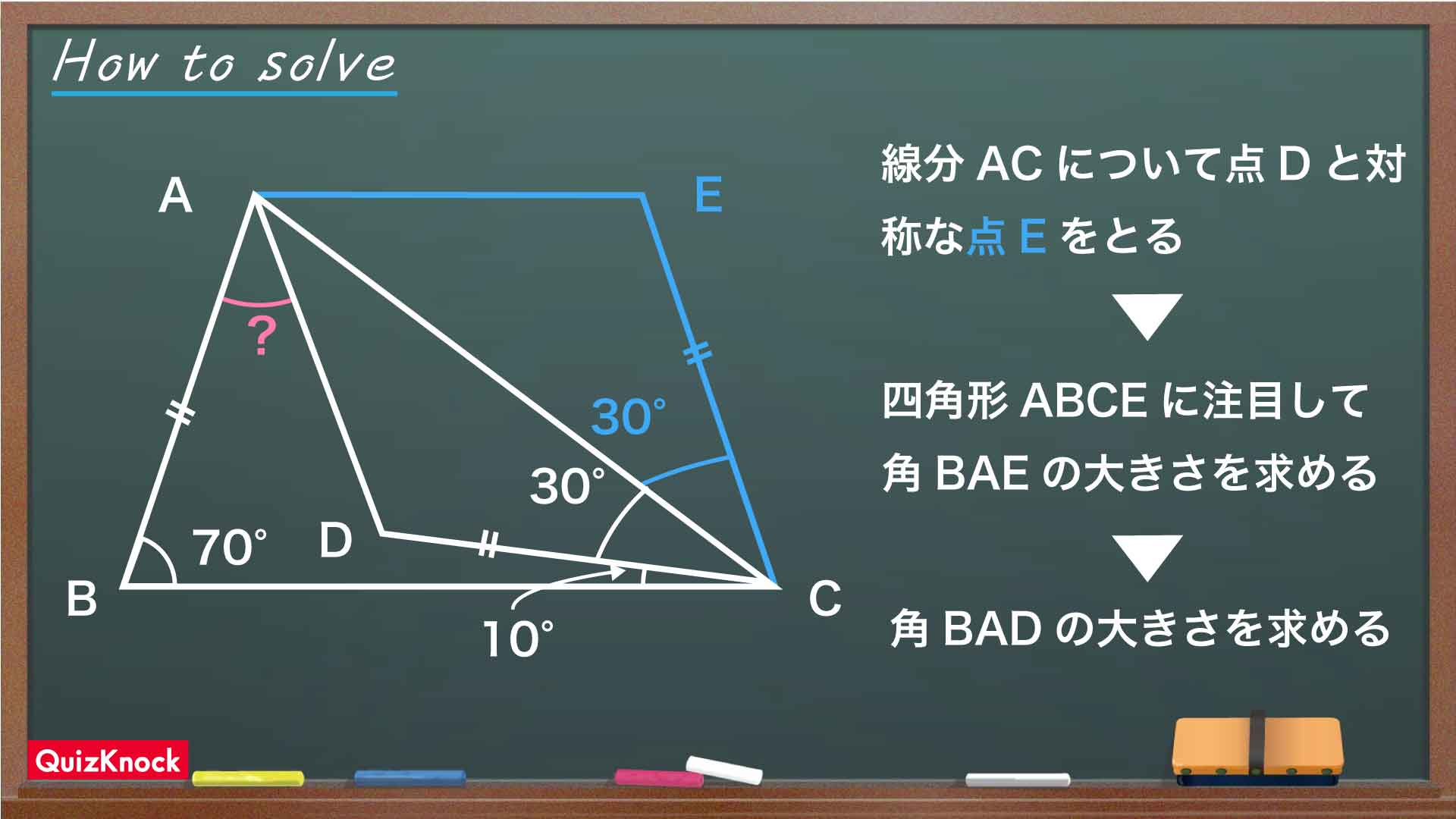
今回の問題の解き方をまとめた図がこちらになります。
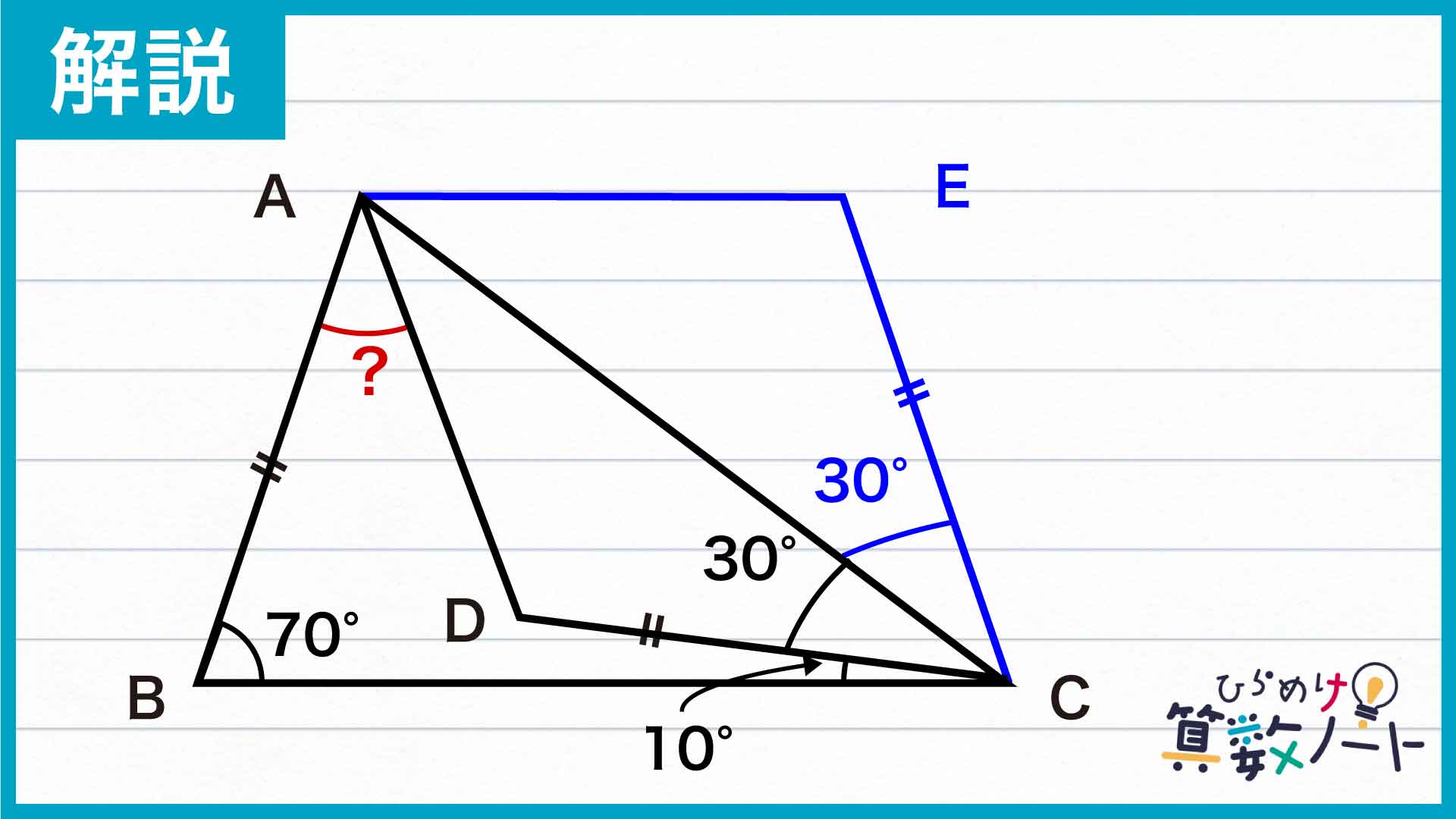
ポイントは、AB=DCという条件に注目して、線分ACについて点Dと対称な点Eをとることです。これを踏まえて解いていきましょう!
点Eをとる
下の図のように点Eをとります。点Eは、線分ACについて点Dと対称な点です。
このとき、三角形ADCと三角形AECは合同なので、DC=ECであり、角DCA=角ECA=30度です。よって、角BCEの大きさは、10+30+30=70度となります。
四角形ABCEについて考える
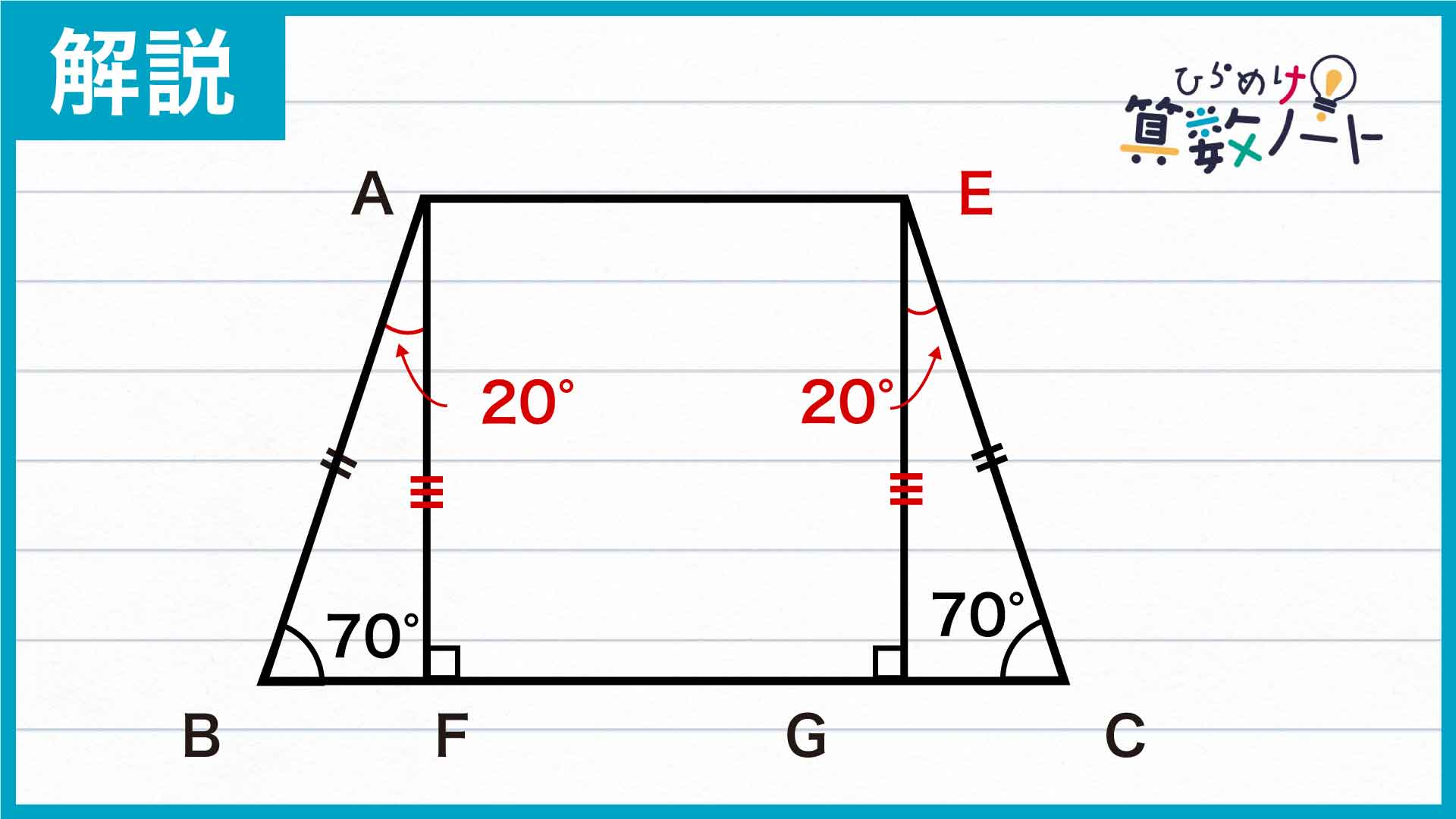
次に、四角形ABCEについて考えてみましょう。点A、点Eから辺BCに垂直な線を引き、辺BCと交わる点をそれぞれ点F、点Gとします。
このとき、三角形ABFと三角形ECGに注目すると、角FABと角GECの大きさは180-70-90=20度であることがわかります。AB=EC、角ABF=角ECG=70度、角FAB=角GEC=20度なので、三角形ABFと三角形ECGは、互いに1つの辺の長さとその両端の角の大きさが等しいという関係にあります。1つの辺の長さとその両端の角の大きさが決まれば三角形はひとつに定まるため、三角形ABFと三角形ECGは合同です。よって、AF=EGとなります。
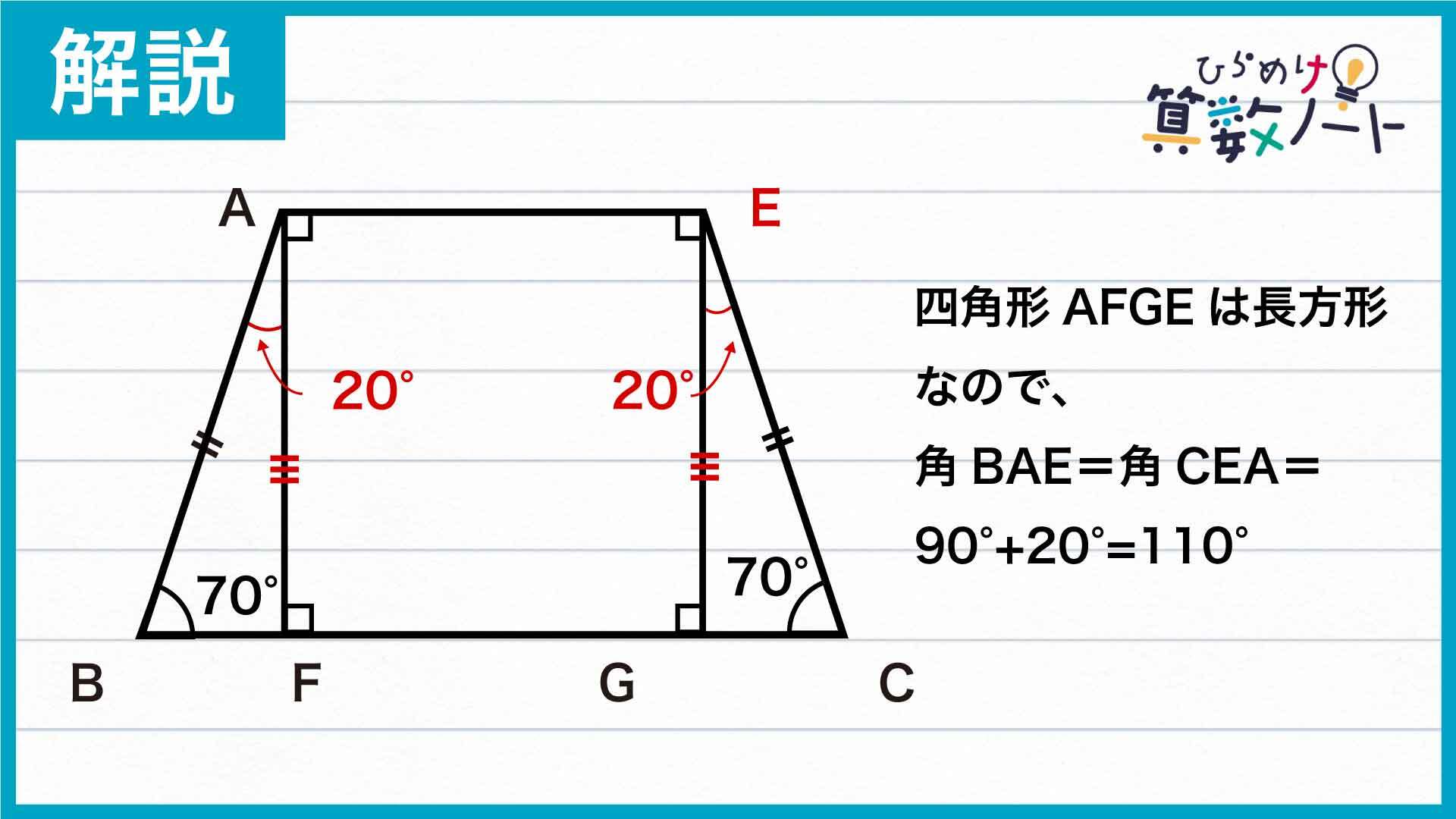
角BAEと角CEAの大きさを求める
四角形AFGEにおいて、辺AFと辺EGの長さは等しく、角AFG=角FGE=90度なので、四角形AFGEは長方形です。よって、角BAEと角CEAの大きさはともに90+20=110度になります。
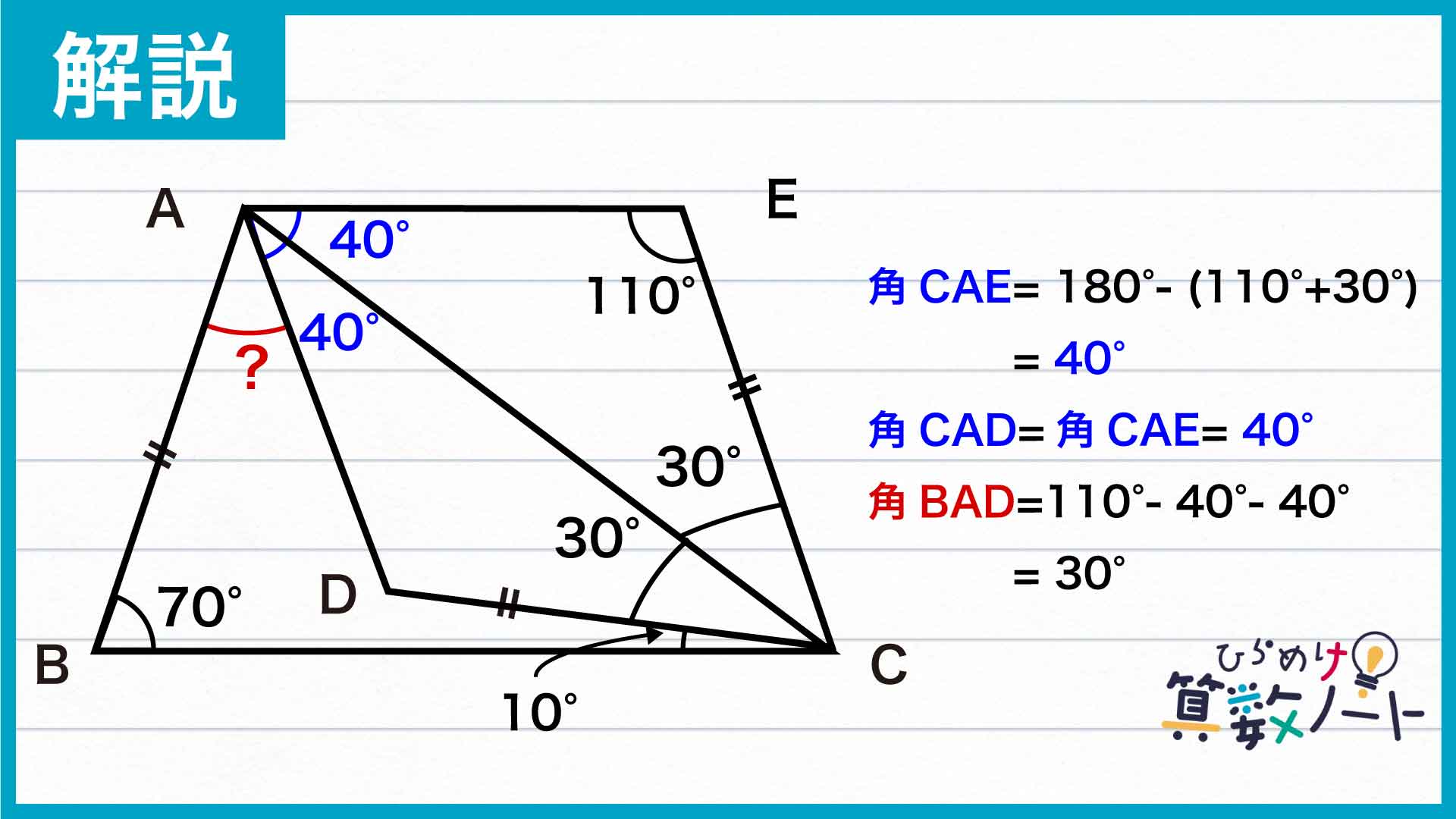
角BADの大きさを求める
角CEAの大きさは110度なので、角CAEの大きさは180-110-30=40度です。また、三角形ADCと三角形AECは合同なので、角CADの大きさも180-110-30=40度です。角BAEの大きさは110度なので、角BADの大きさは110-40-40=30度と求められます。
答え:30度それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)









.jpg)







