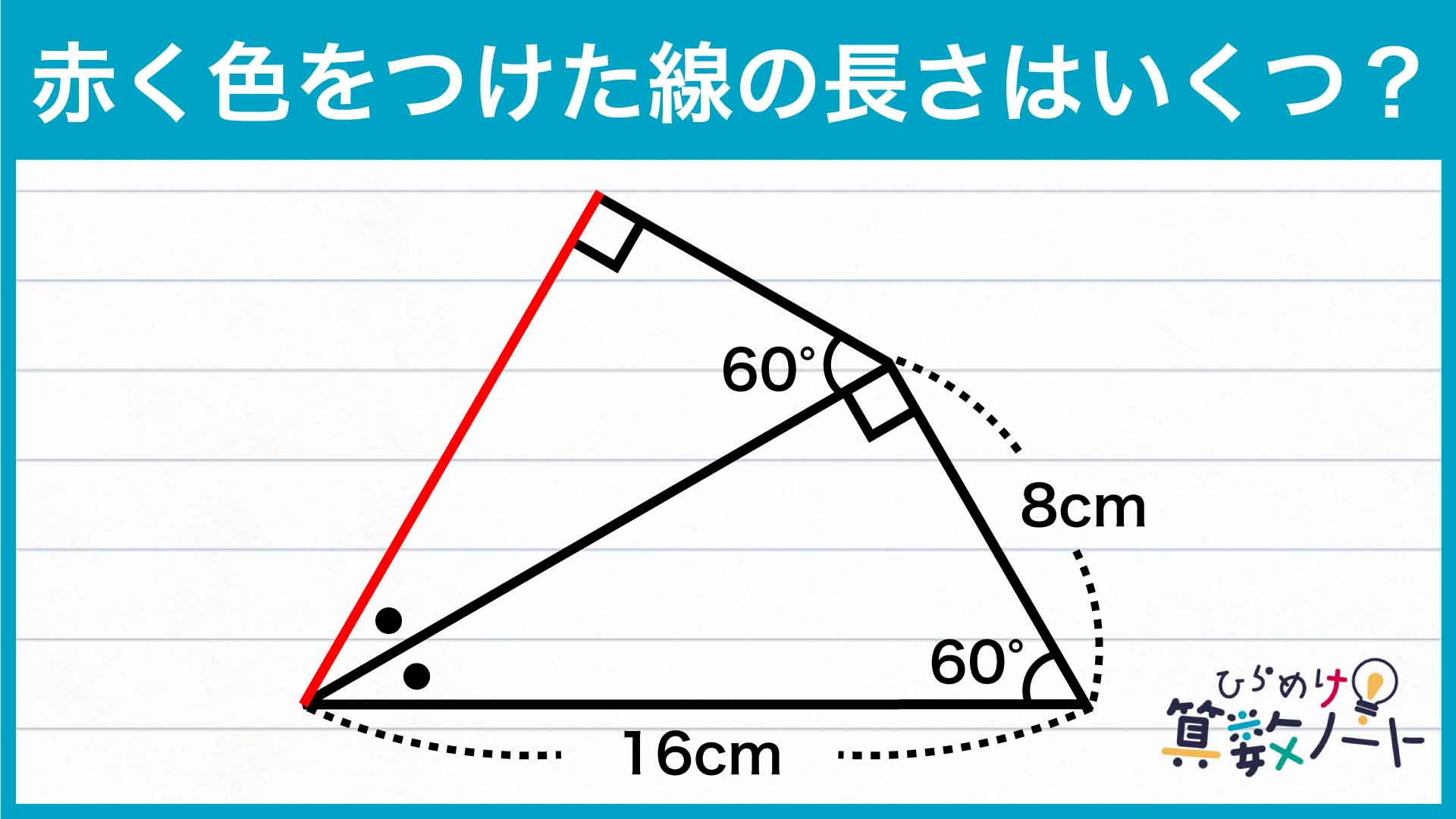
ひらめけ!算数ノートp.139小学生で解ける「辺の長さ」を求める問題にチャレンジ!あなたは解けますか?
理系松林 陸2024.07.24
ヒント
下の図のように、問題の図形に内角の大きさが30度、60度、90度の直角三角形をつけ足します。さらに、点Aから点Eまでの点を振ります。
このとき、角ACB+角ACD+角DCE=90+60+30=180度であることから、点B、点C、点Eは一直線上に並びます。さらに、角CDA+角CDE=90+90=180度であることから、点A、点D、点Eは一直線上に並びます。したがって、図形ABEは大きな三角形になります。
さらに、角BAC=角DAC=180-(90+60)=30度で、角BAE=30+30=60度となります。よって、角ABE=角AEB=角BAE=60度であることから、三角形ABEは正三角形になります。
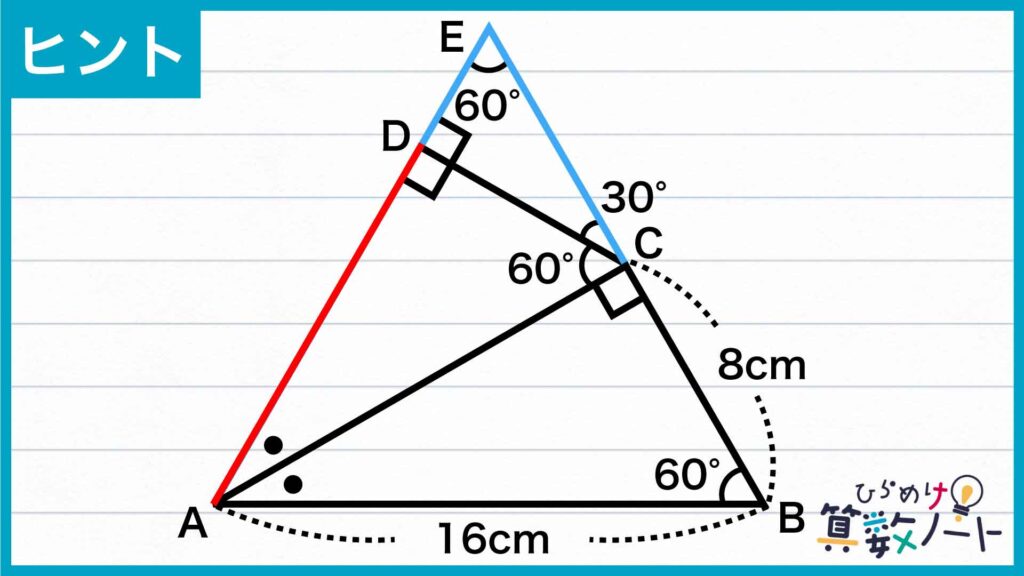
つけ足した直角三角形をどのように活用できるでしょうか?
3ページ目:【答え&解説】つけ足した直角三角形を利用して辺の長さを求めます。答えと解説はこちらへ
Amazonのアソシエイトとして、当サイトは適格販売により収入を得ています。
関連記事
この記事を書いた人

松林 陸
京都大学大学院理学研究科・修士2年の松林 陸です。普段は大学のサークルでクイズをしています。
大学では物理学を専攻しています。好きなものはクイズと旅行と科学。読者の方の日々に「ちょっとした学び」が生まれるような記事を書けるように頑張ります。
松林 陸の記事一覧へ




















.jpg)







