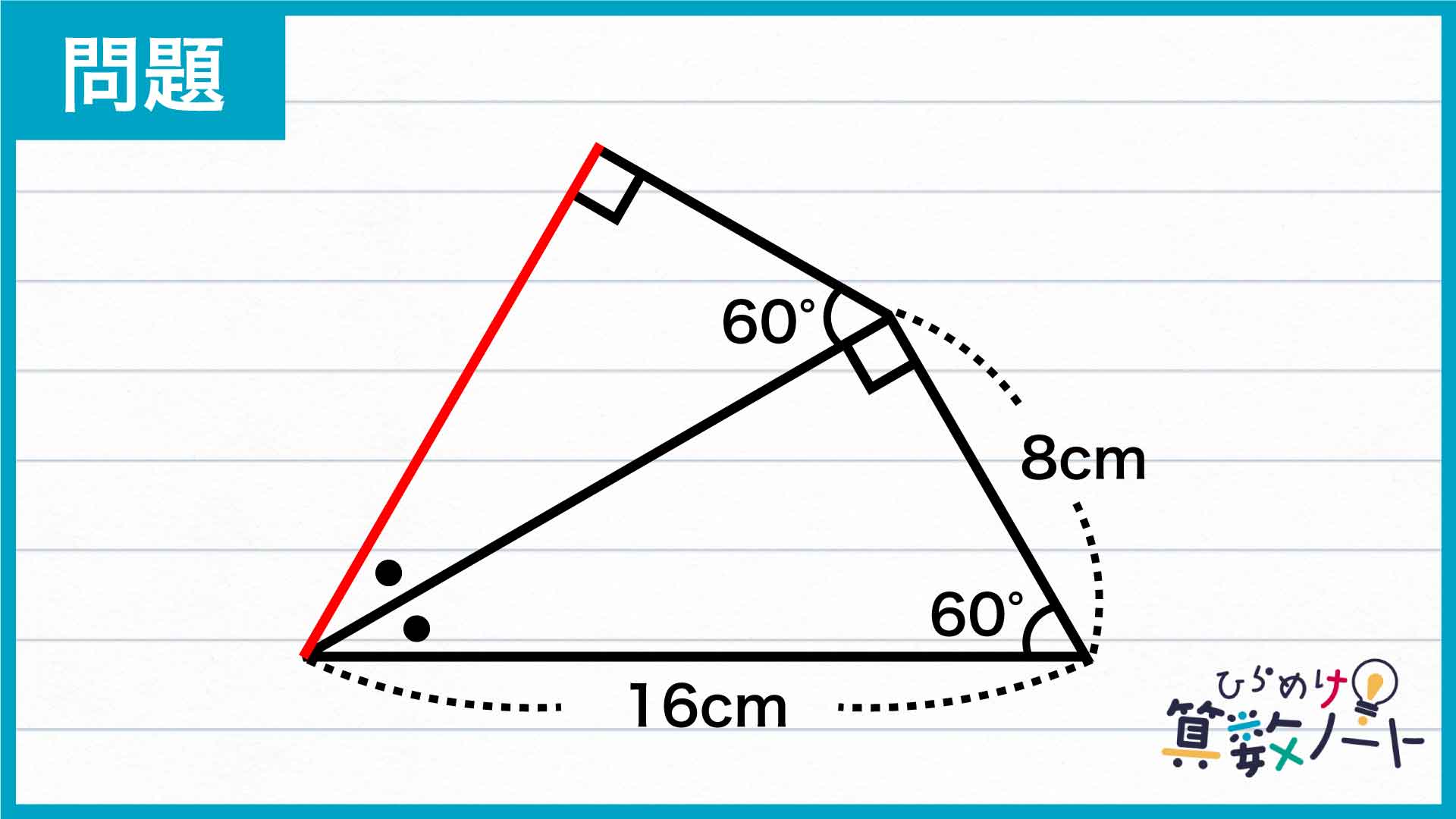
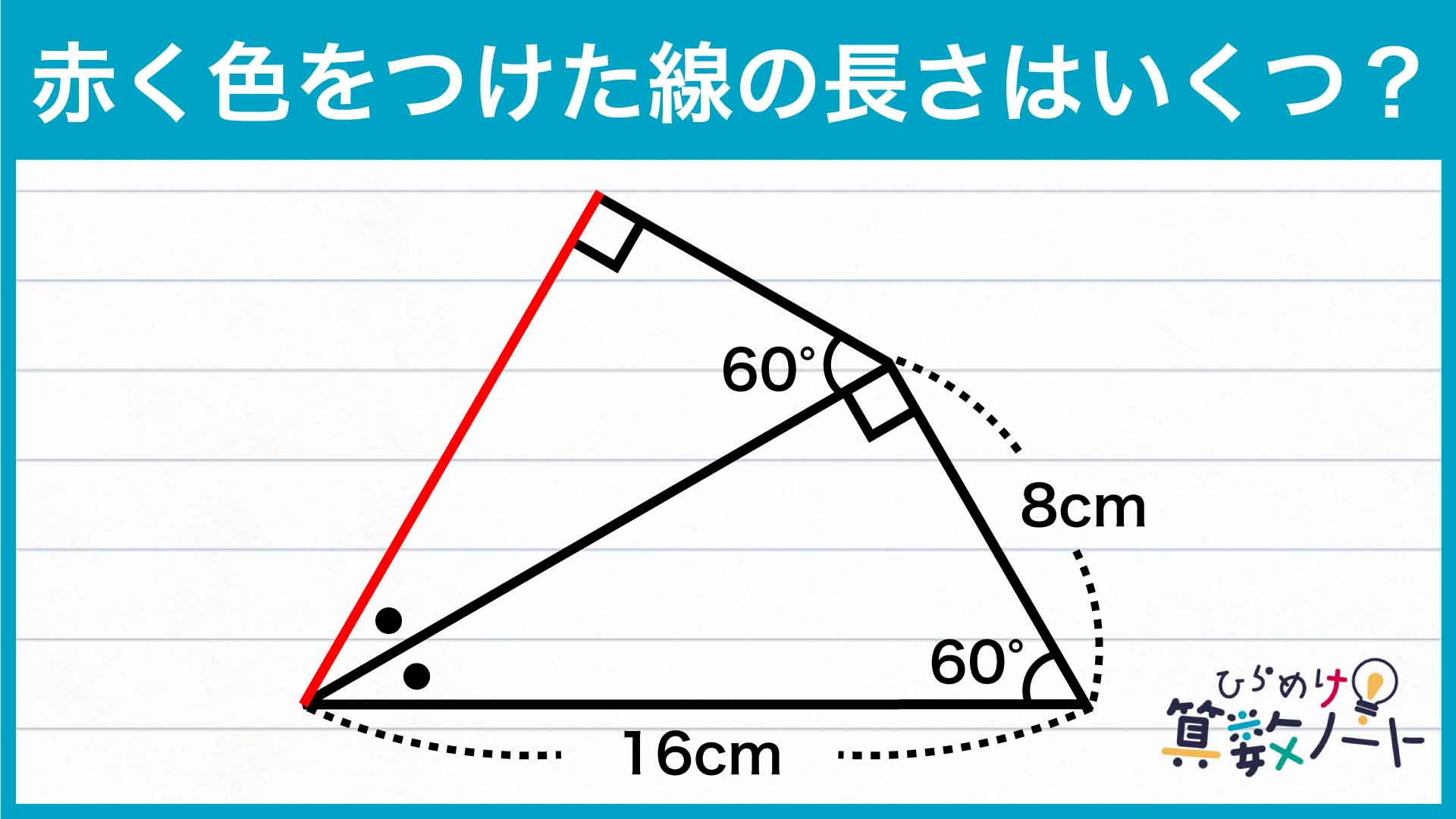
問題はこちら
前ページ:自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の問題を解くうえで重要なポイントを以下にまとめました。
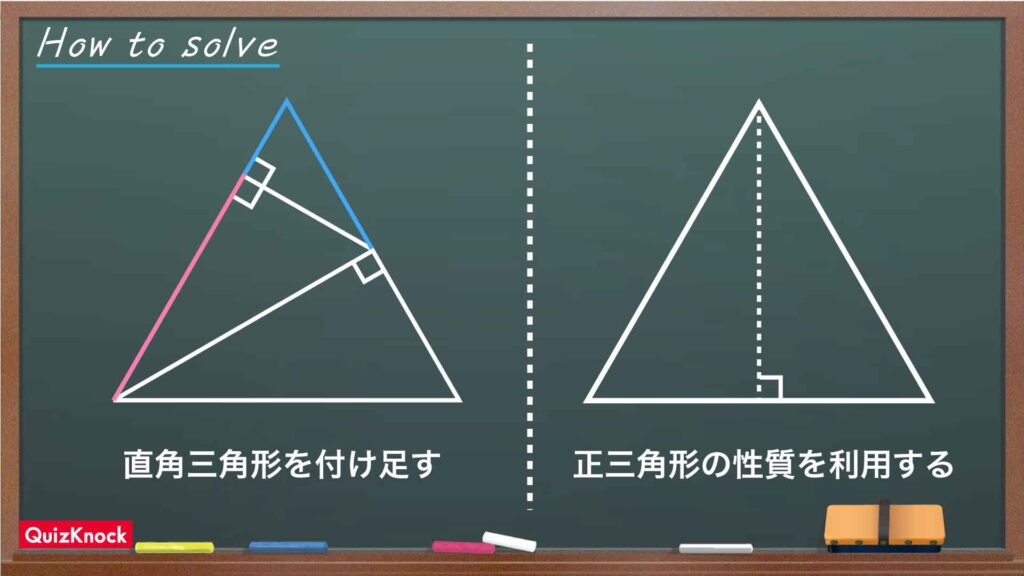
整理すると、
- 直角三角形をつけ足す
- 正三角形の性質を利用する
の2点です。これらのポイントを踏まえながら、問題を解いていきましょう。
直角三角形をつけ足す
解説のために、下のように点Aから点Dまでの点を振ります。
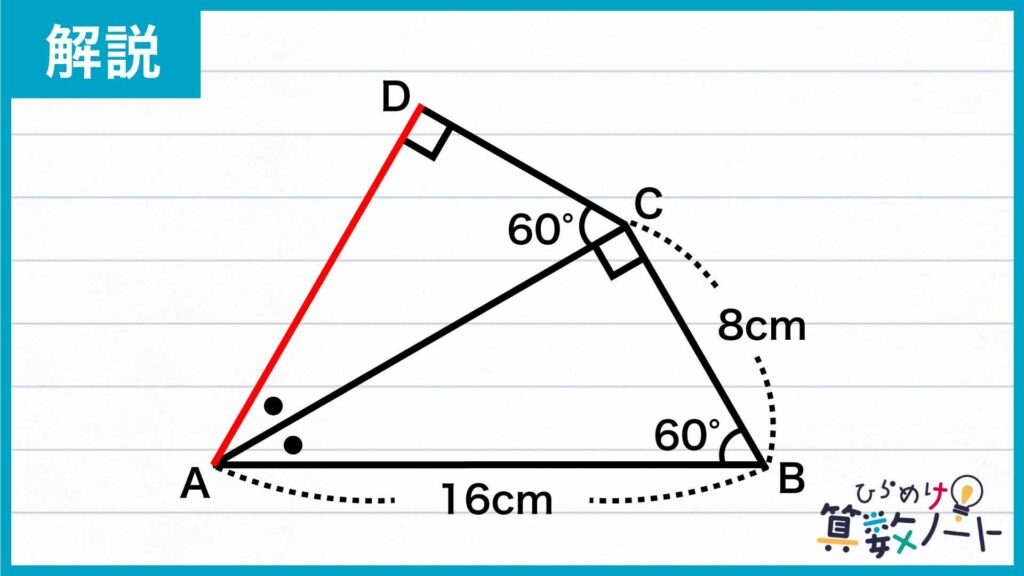
続いて、下の図のように問題の図形に内角の大きさが30度、60度、90度の直角三角形CDEをつけ足します。
角ACB+角ACD+角DCE=90+60+30=180度となることから、点B、点C、点Eは一直線上に並びます。さらに、角CDA+角CDE=90+90=180度となることから、点A、点D、点Eは一直線上に並びます。したがって、図形ABEは大きな三角形になります。さらに、角BAC=角DAC=180-(90+60)=30度で、角BAE=30+30=60度となります。よって、角ABE=角AEB=角BAE=60度であることから、三角形ABEは正三角形になります。
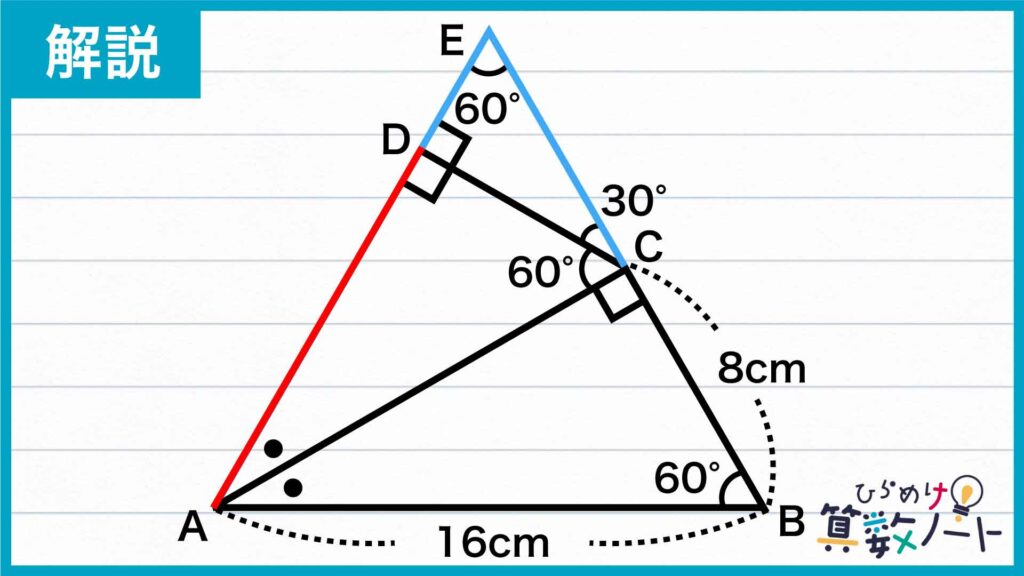
正三角形の性質を利用する
三角形ABEは正三角形なので、AB=AE=BE=16cmであることがわかります。また、BC=8cmなので、CE=BE-BC=16-8=8cmになります。
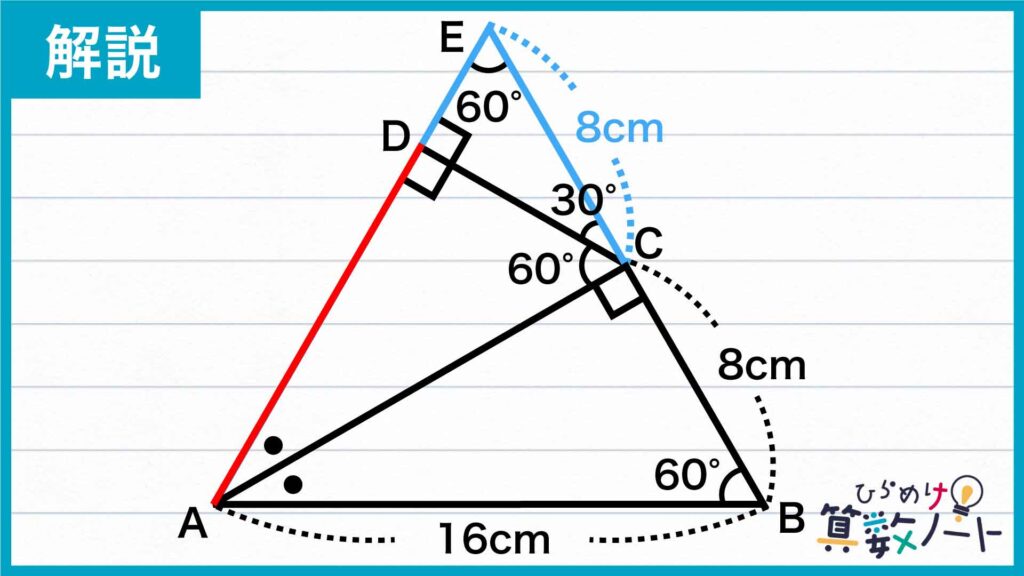
次に、直角三角形CDEに注目します。直角三角形CDEと合同な三角形CDFを用意し、下の図のように2つの三角形を辺CDでぴったり合わせます。
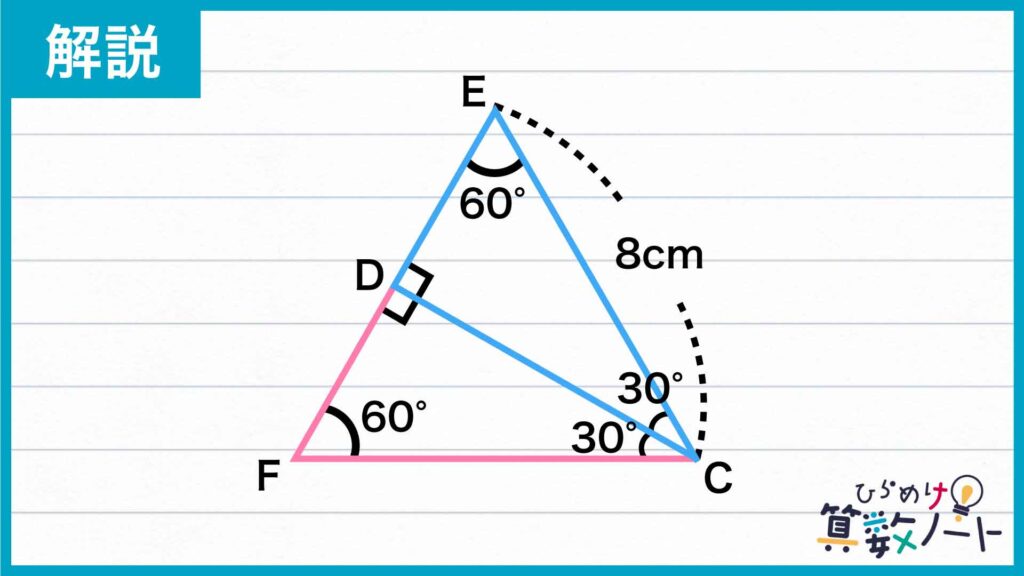
このとき、角CDE+角CDF=180度より、点E、点D、点Fは一直線上に並びます。したがって、図形CEFは三角形となり、さらに三角形CEFの3つの内角が全て60度なので、三角形CEFは正三角形です。
よって、EF=CE=8cmとなり、三角形CDEと三角形CDFが合同であることからDE=DFなので、DE=8÷2=4cmとなります。
したがって、求める辺ADの長さは、AE-DE=16-4=12cmとなります。
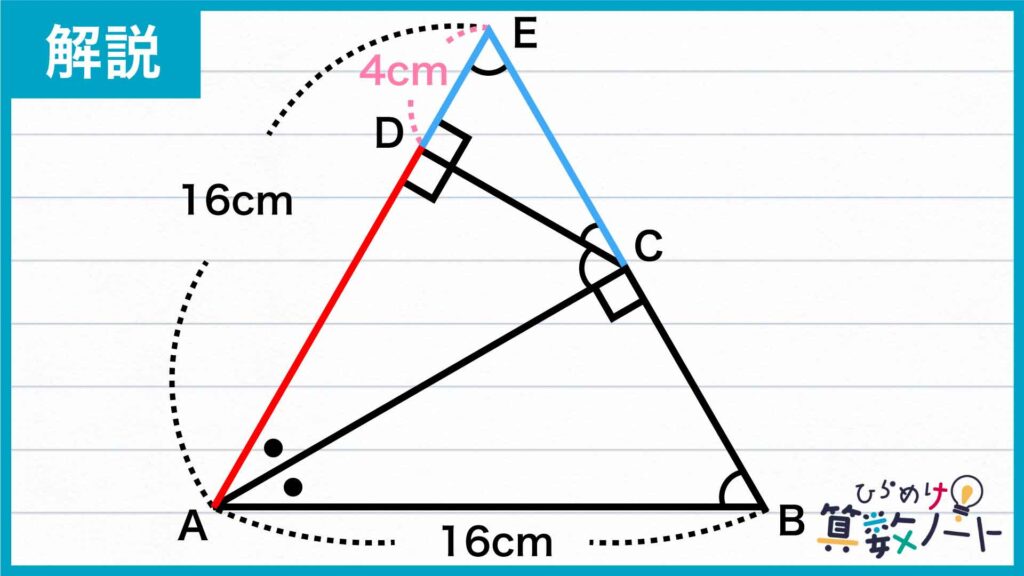
答え:12cm
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)









.jpg)







