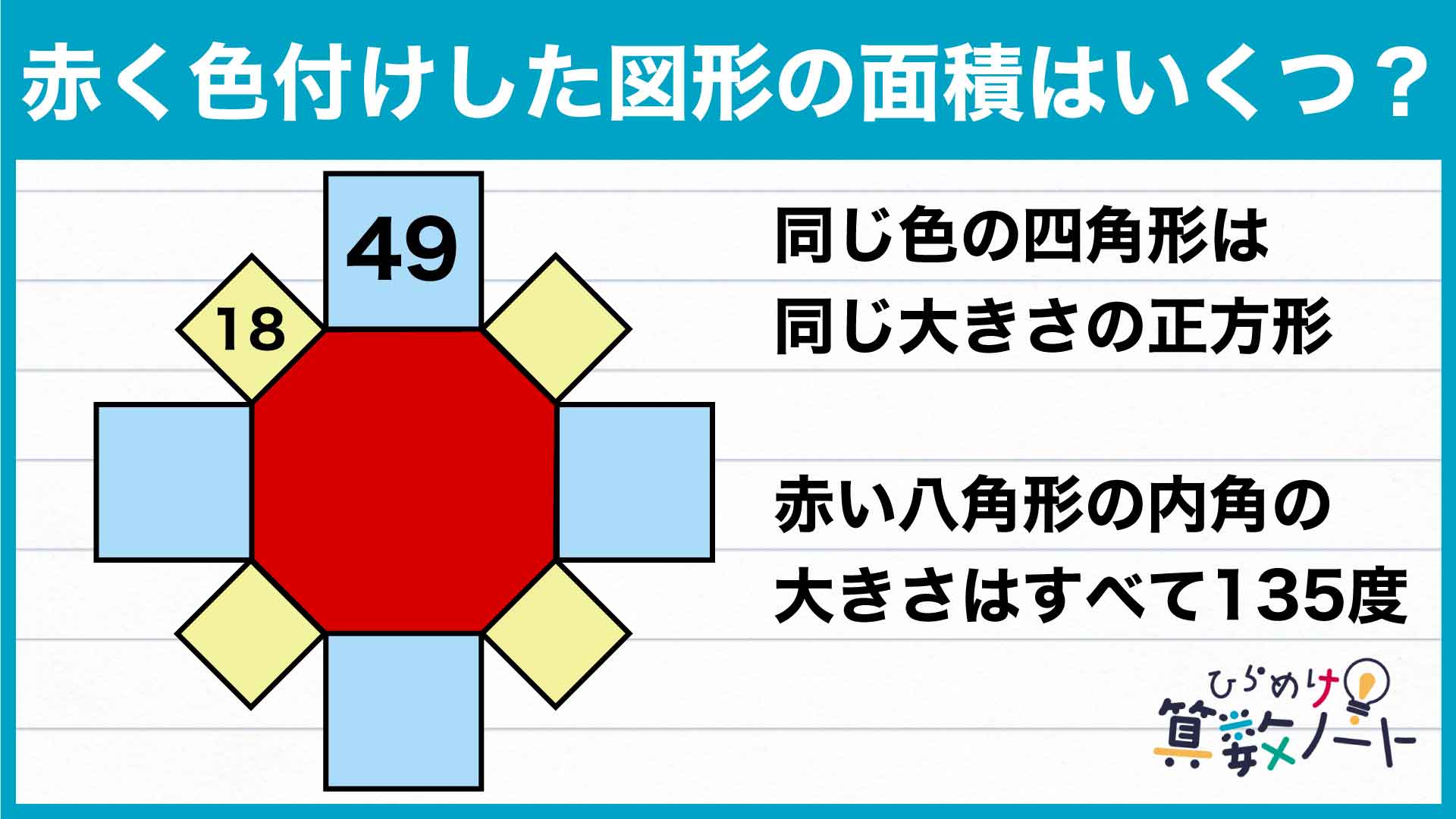
問題はこちら
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
この問題の解き方をまとめた図がこちらです。
ポイントは、なるべくシンプルな図形を作ってからそれぞれの面積を求めていくことです。
では、このポイントを踏まえつつ解いていきましょう!
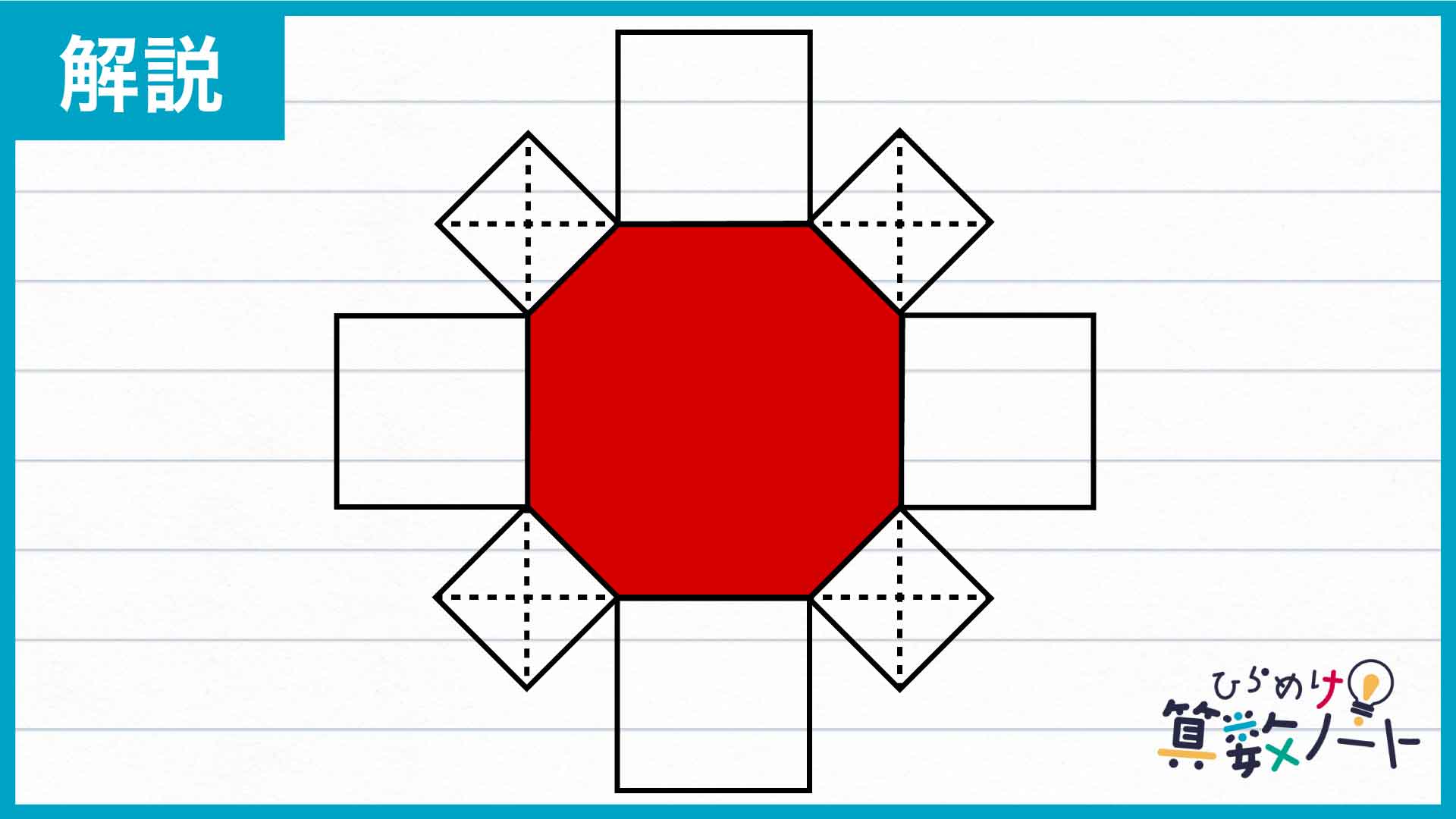
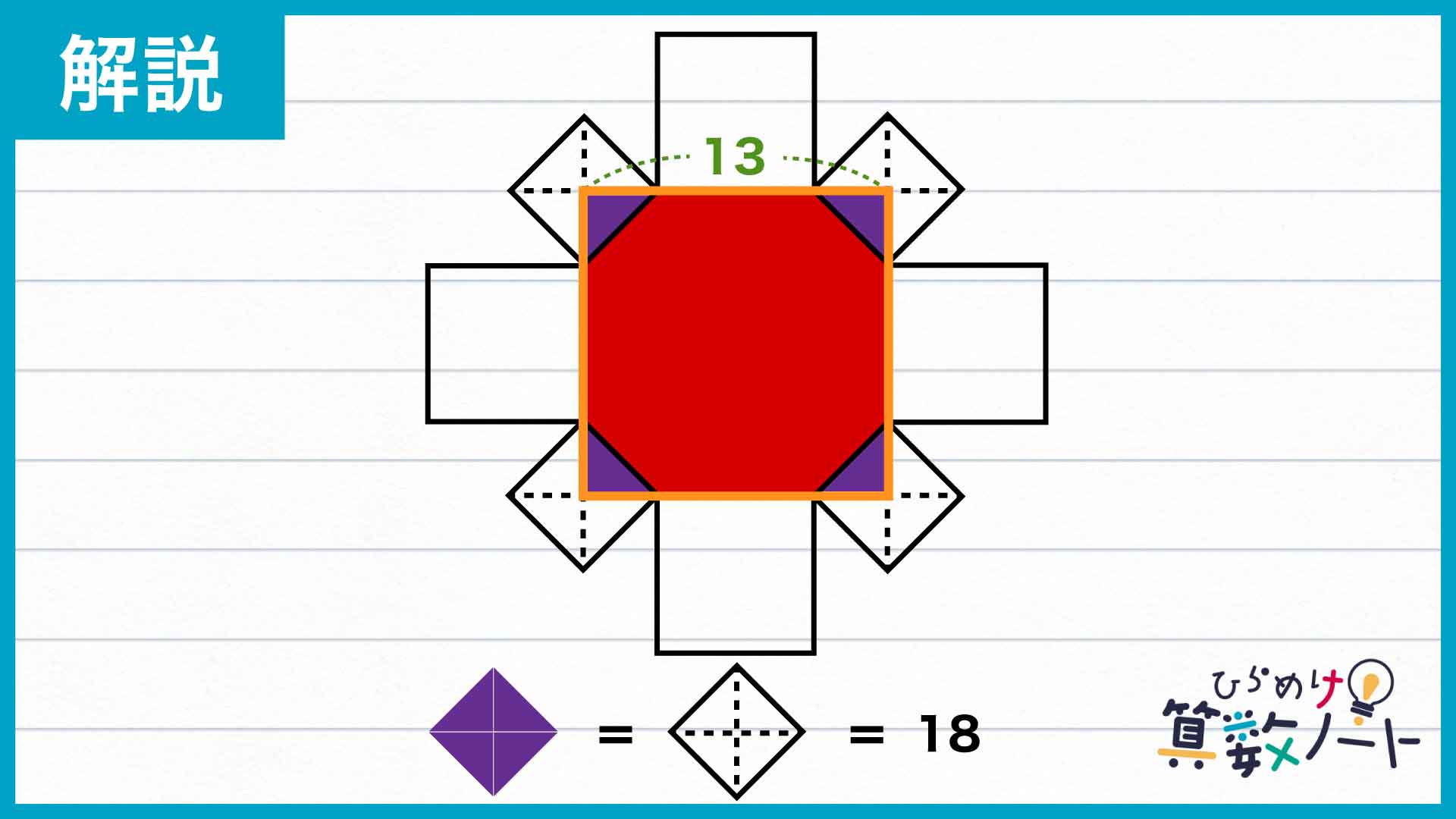
大きな正方形を作る
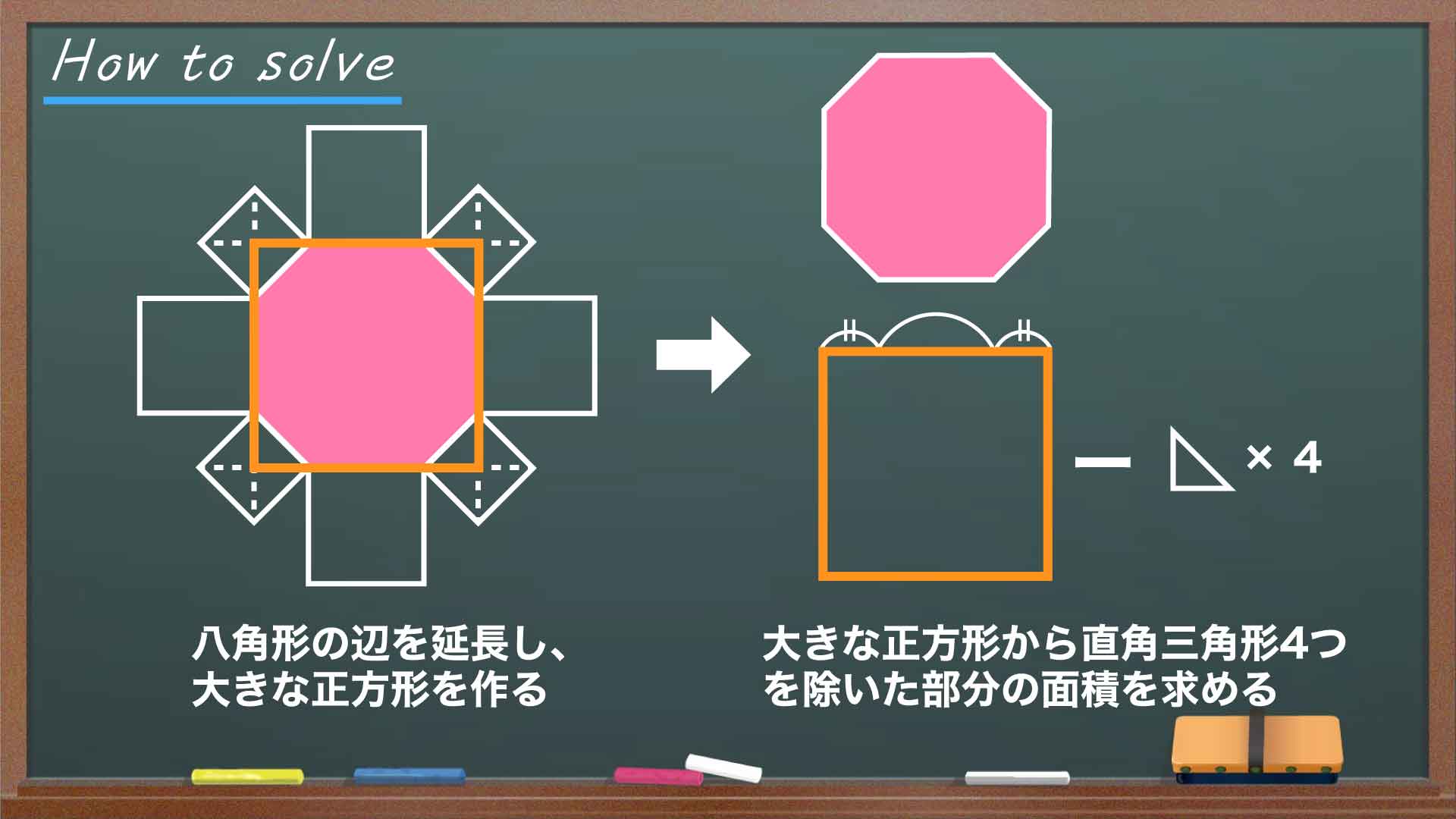
塗りつぶされた図形はやや複雑な八角形なので、このまま面積を求めるのは容易ではありません。そこで、八角形の辺のうち大きい方の正方形と重なっている部分を延長してみます。
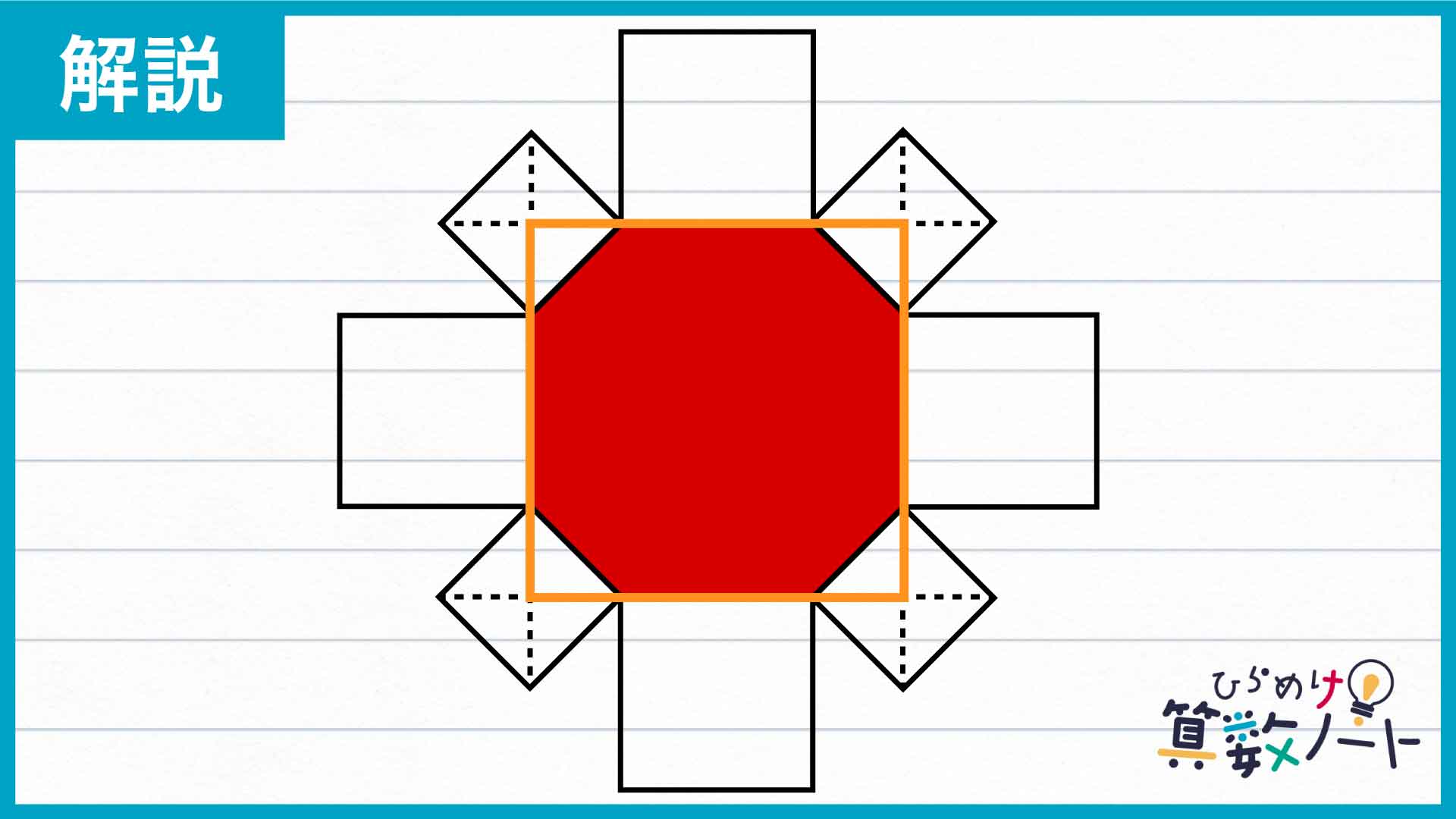
大小それぞれの正方形は隙間なく均等に配置されており、八角形の内角の大きさはすべて135度であるため、延長された辺同士は直角に交わり、小さい正方形の対角線と重なります。延長された辺同士が交わる点を下の図のように結ぶと、さらに大きな正方形が現れました。
求める八角形の面積は、オレンジ色で囲まれた正方形から4つの直角三角形を除いた部分の面積にあたることがわかります。
オレンジの正方形の面積を求める
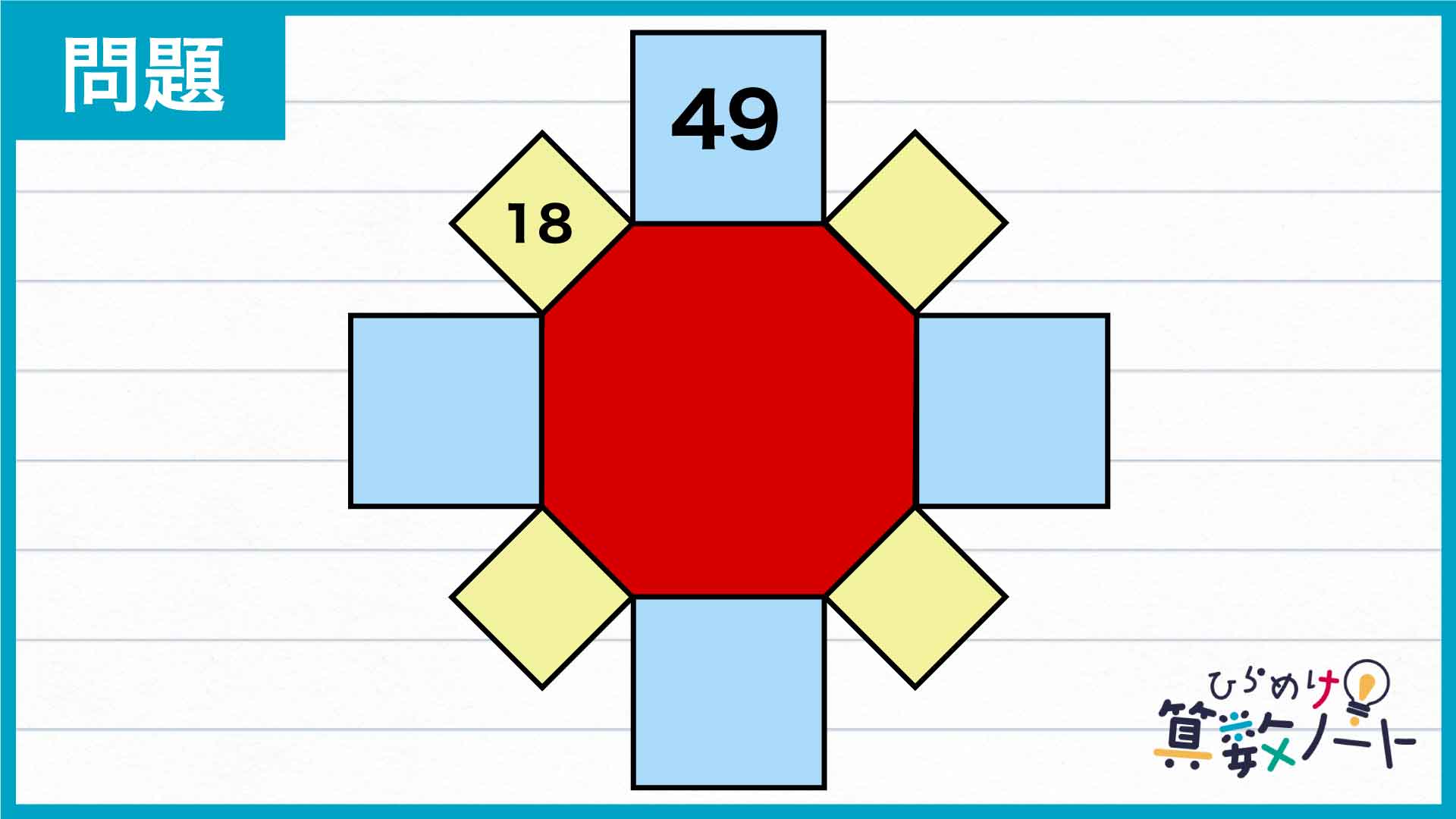
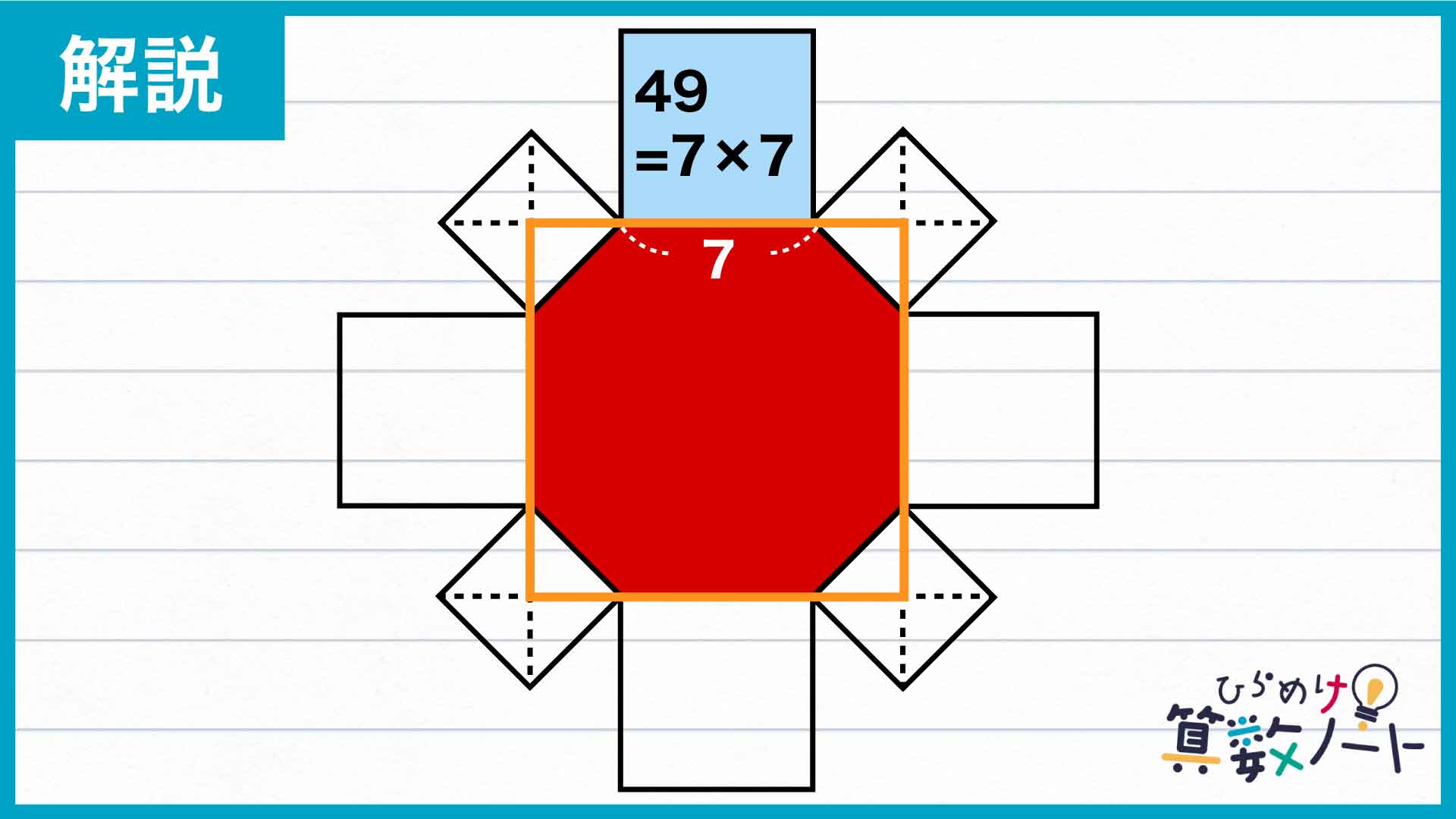
八角形の辺を延長して作った正方形について、1辺の長さを考えます。ぐるりと並べられた2種類の正方形のうち大きい方の面積は49なので、その1辺の長さは7です。
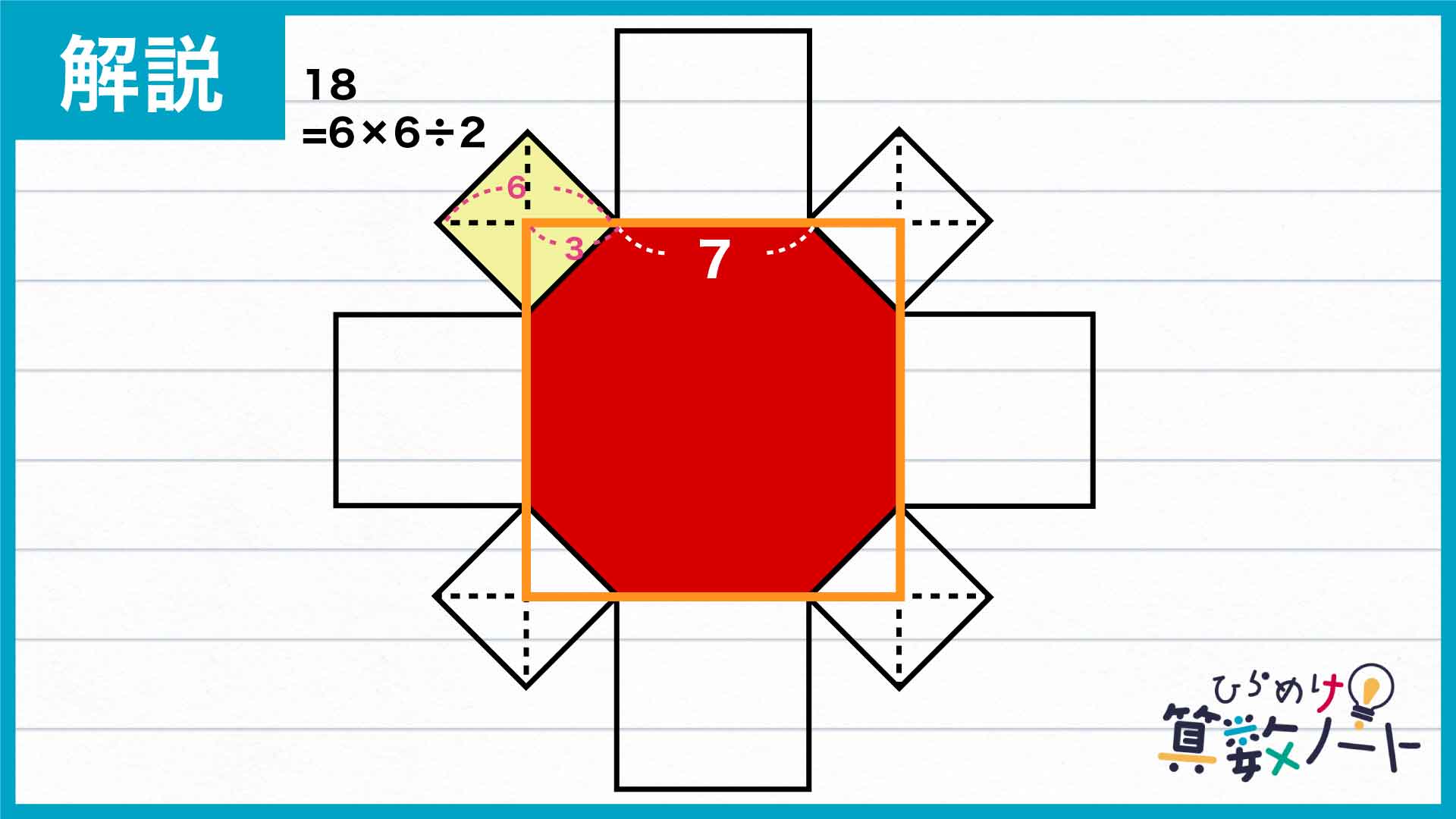
正方形の面積は、(1辺)×(1辺)以外に(対角線)×(対角線)÷2という式を用いて面積を求めることもできます。よって、小さい正方形の面積が18=6×6÷2であることから、小さい正方形の対角線の長さは6です。
以上のことから、オレンジ色で囲まれた正方形の1辺の長さは3+7+3=13となります。求めるのはこの正方形から小さな直角三角形4つを除いた部分の面積ですが、この直角三角形をよく見ると小さな正方形を4分割したものであることがわかります。
よって、除かなければならない直角三角形の面積の合計は小さな正方形1つ分と同じく18です。以上のことから、求める八角形の面積は13×13-18=151であるとわかります。
答え:151
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)









.jpg)







