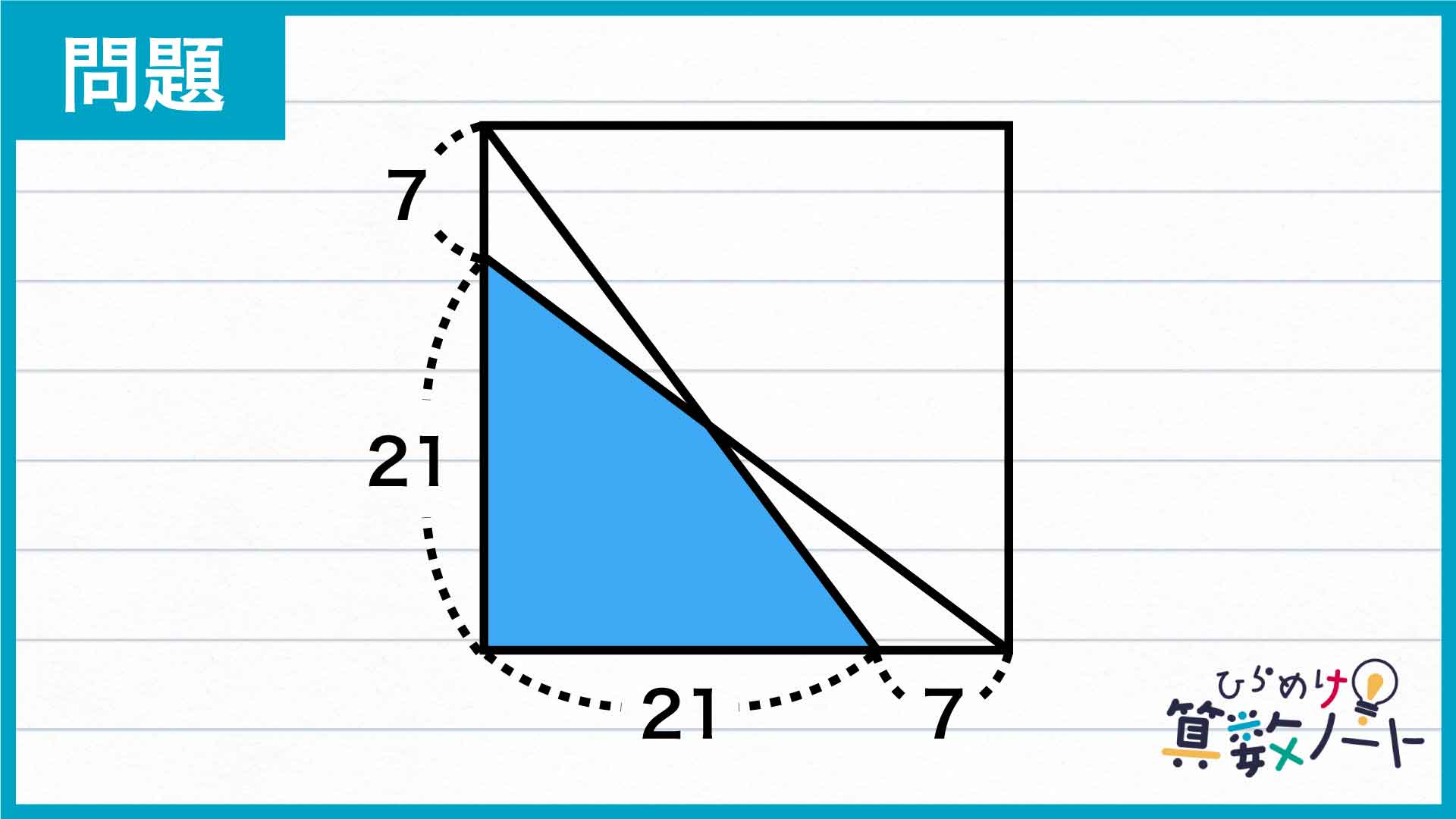
問題はこちら
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の解き方をまとめた図がこちらです。
今回のポイントは、「面積を求められる図形との面積比を求める」ことです。
このポイントをもとに、問題を攻略していきましょう!
図形を観察する
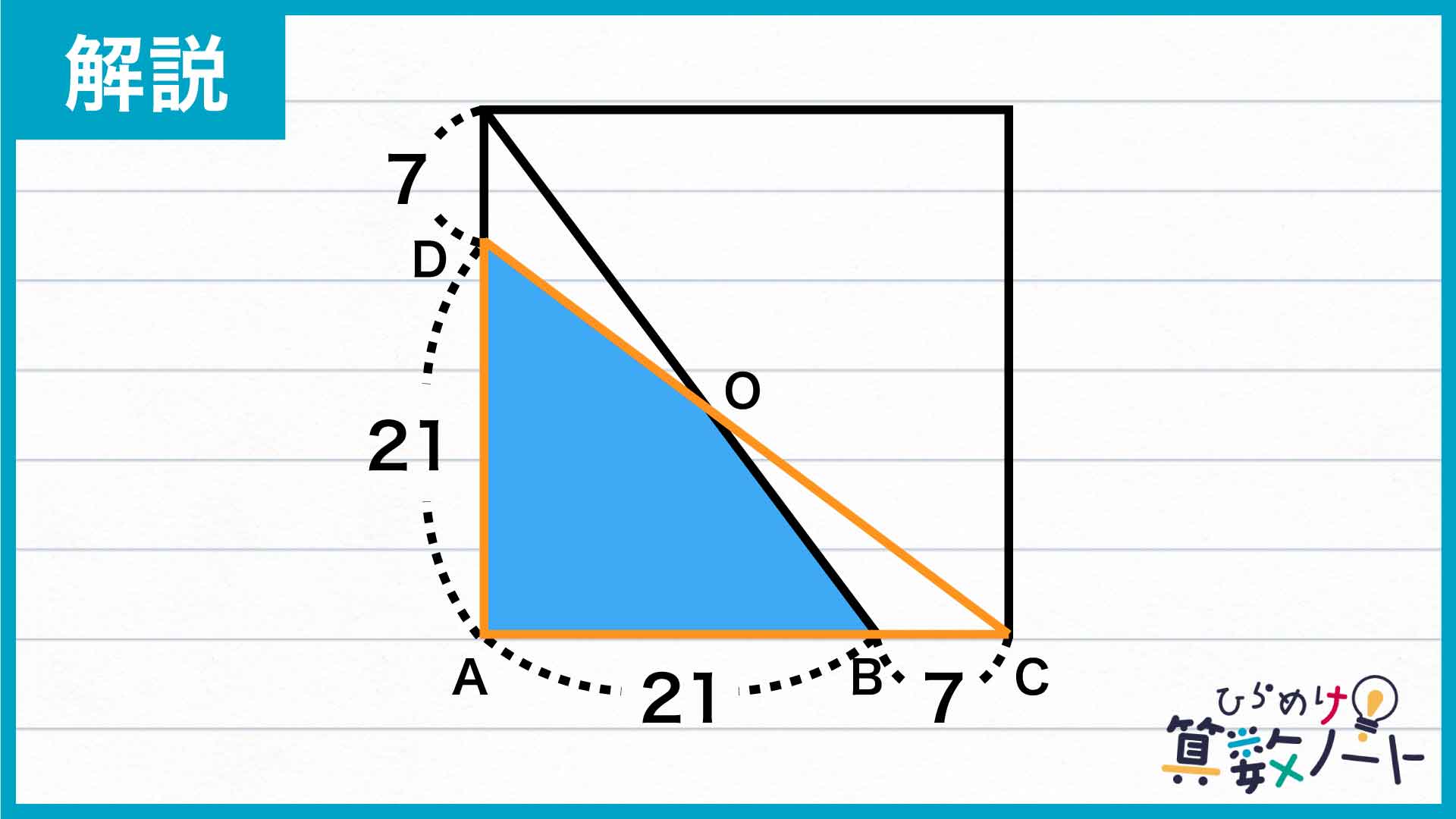
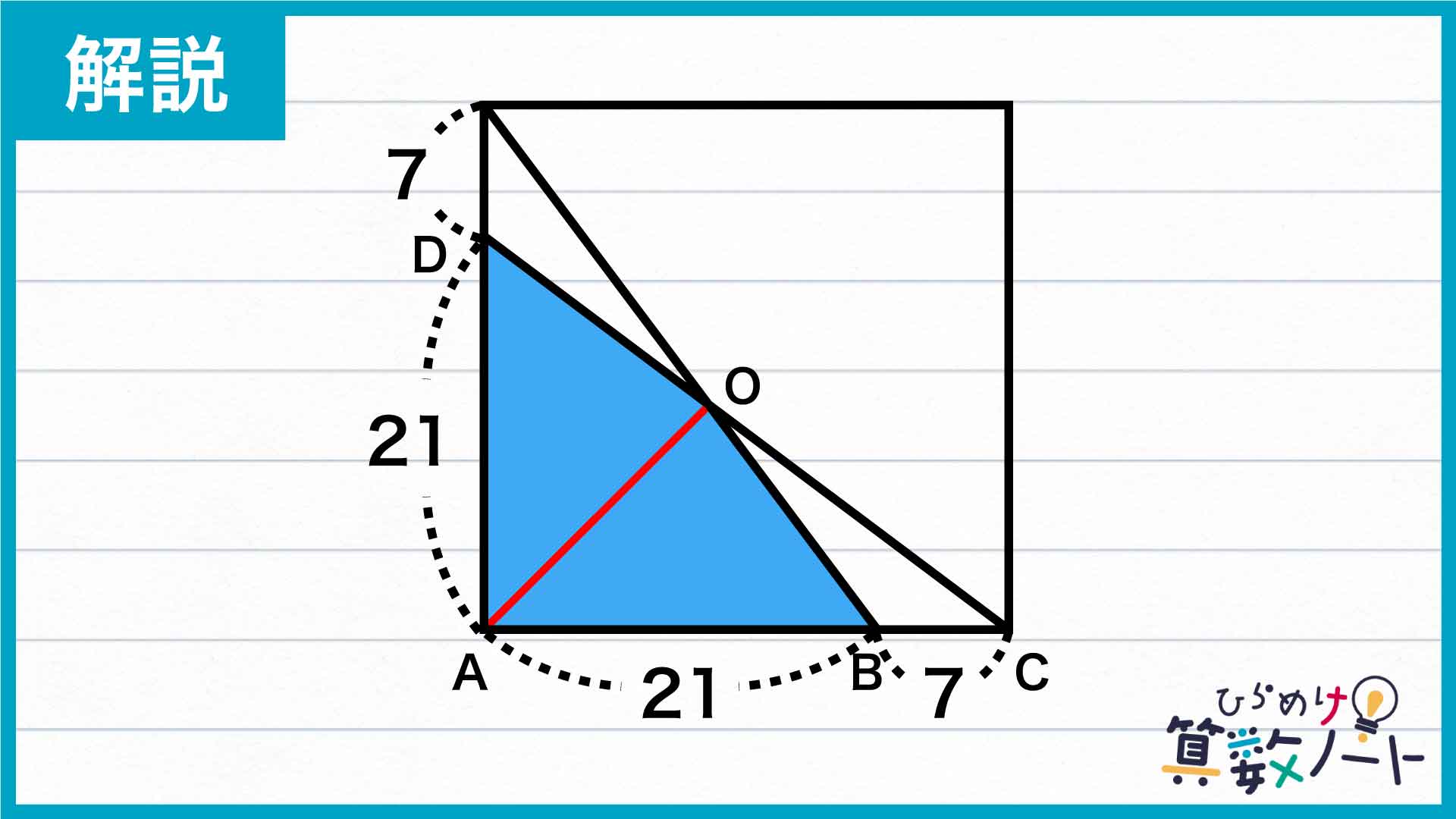
下の図のように点O、A、B、C、Dをおきます。
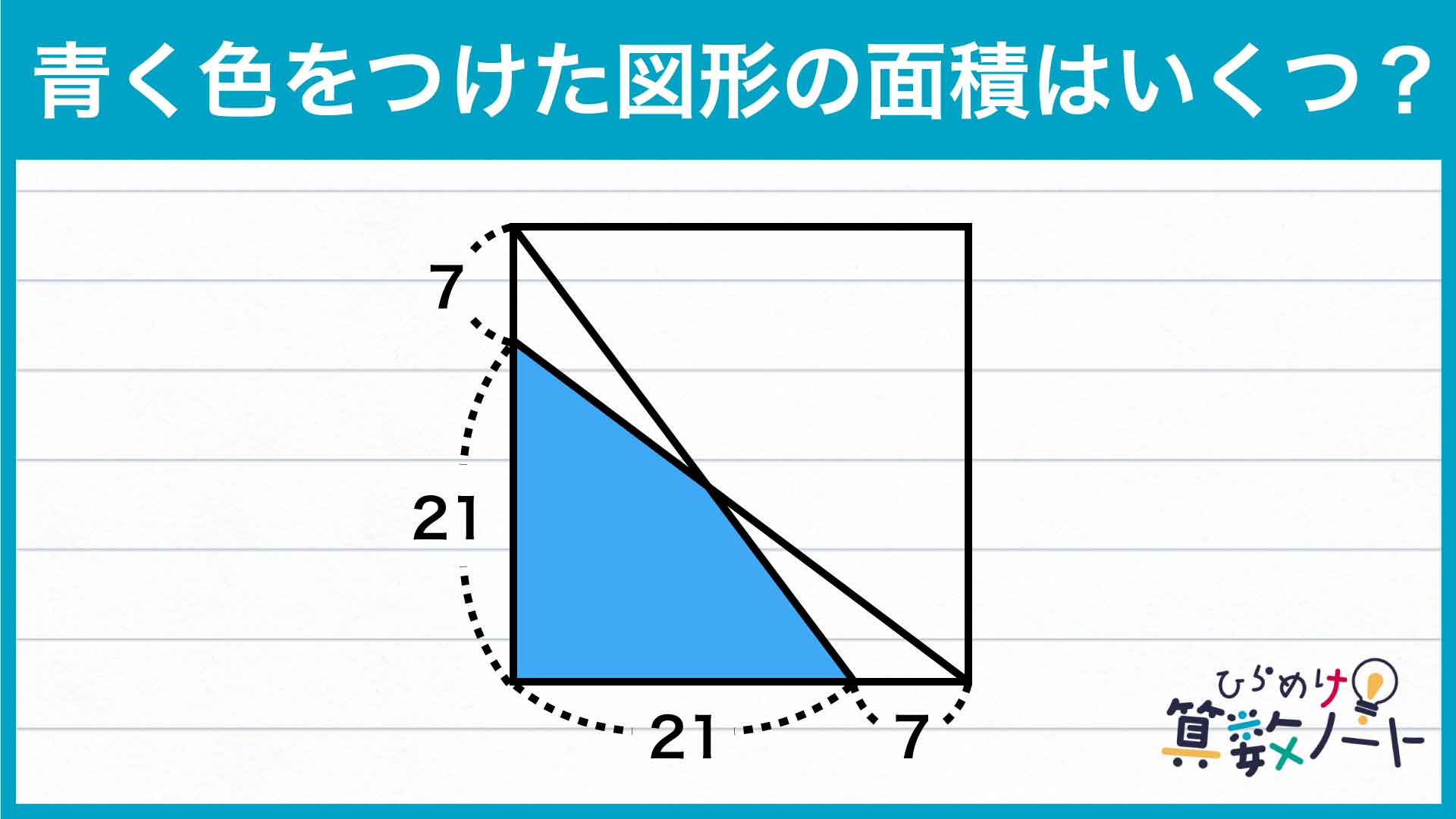
これを見ると、青く色をつけた四角形は、三角形ACDに含まれていることがわかります。また、三角形ACDは底辺も高さも与えられているので、面積を求められる図形であることもわかります。
三角形ACDとの面積比を考える
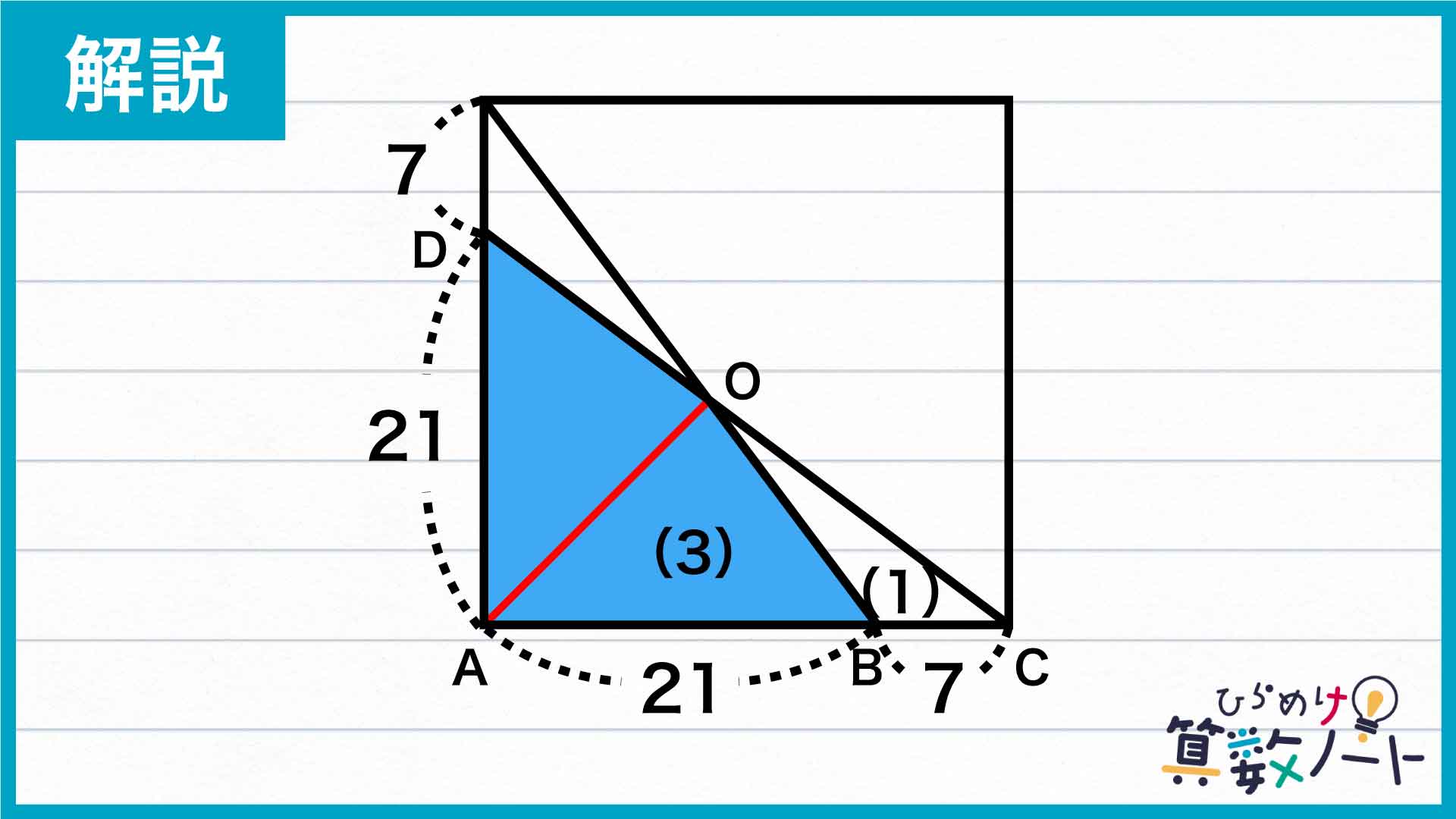
下の図のように、青く色をつけた図形を半分に分割する赤色の線を引きます。
この線によってできた三角形OABと三角形OBCに注目します。2つの三角形は、高さが等しいです。したがって、その面積比は底辺の長さの比から、三角形OAB:三角形OBC=21:7=3:1とわかります。ここから、三角形OABと三角形OBCの面積をそれぞれ(3)、(1)と表します。
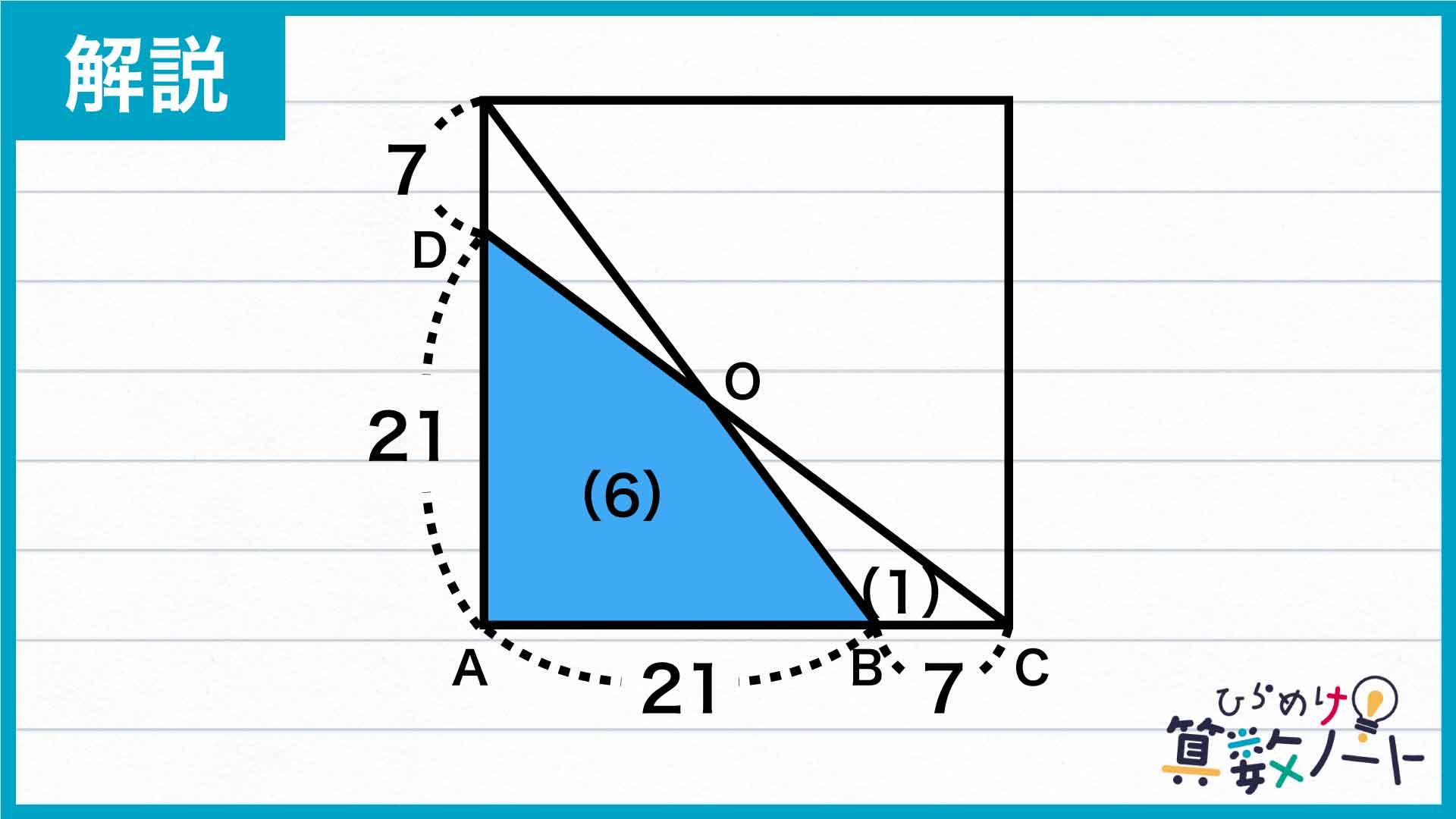
また、三角形OADは三角形OABと合同な図形であるので、面積比は(3)です。そのため、青く色をつけた四角形の面積は(6)とわかります。
したがって、三角形ACDの面積は(7)であるので、青く色をつけた四角形の面積は、三角形ACDの面積の7分の6であることがわかります。
以上より、青く色をつけた四角形の面積は、28×21÷2×6/7=252となります。
答え:252
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】











.jpg)








.jpg)







