解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
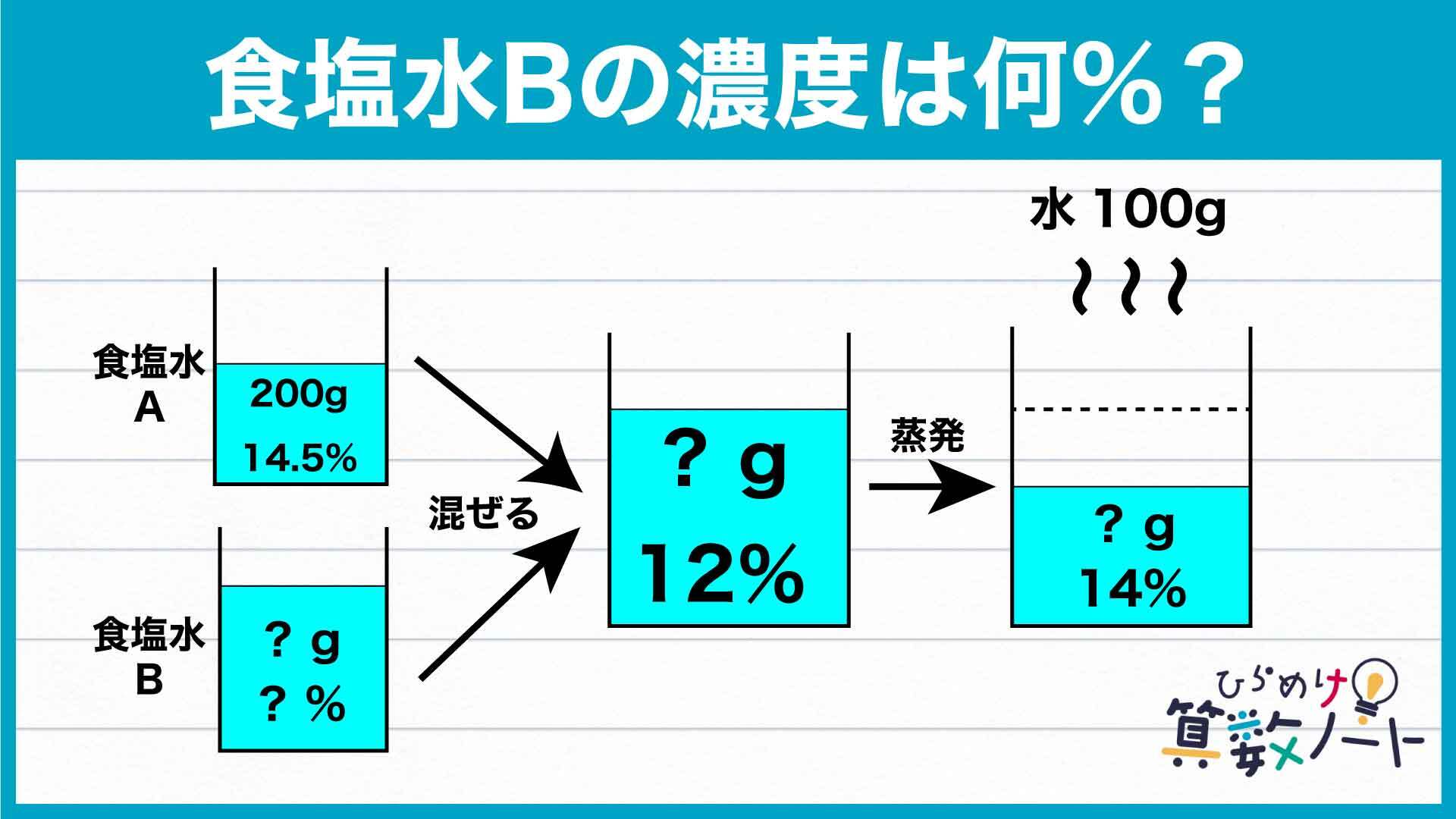
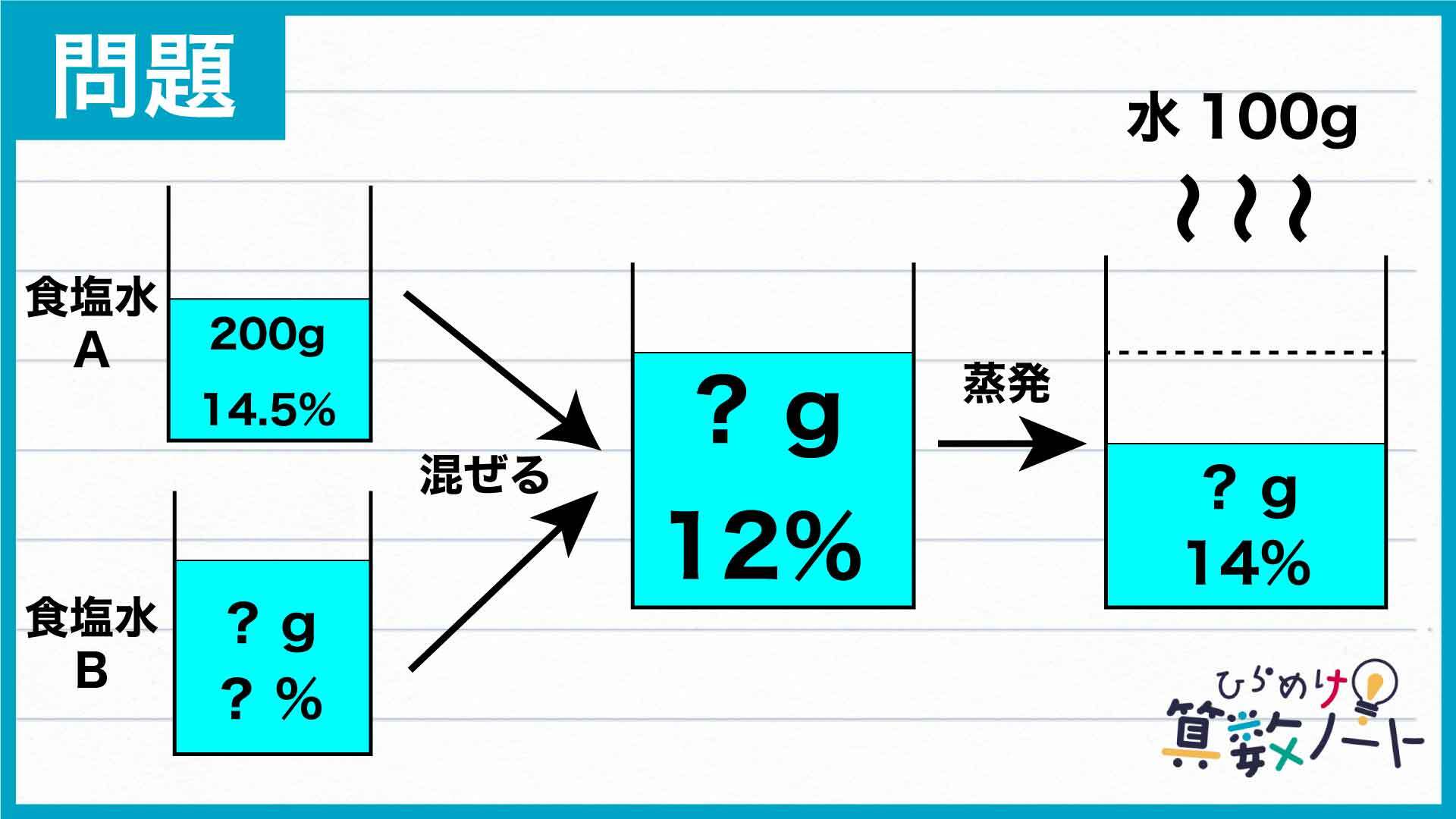
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
この問題の解き方をまとめた図がこちらです。
ポイントは、濃度の変化をヒントにAとBの合計量や食塩の量を求めていくことです。
では、このポイントを踏まえつつ解いていきましょう!
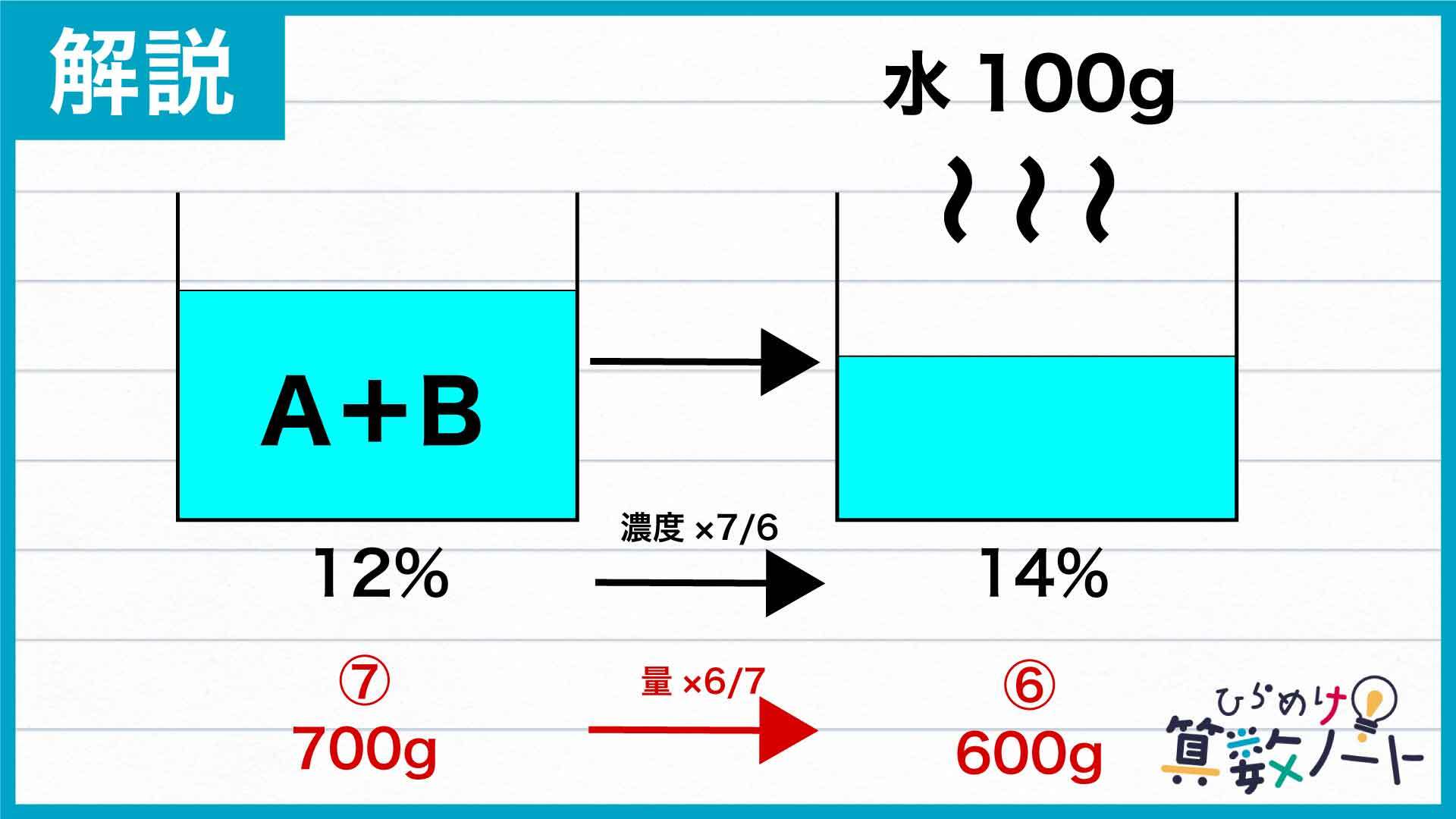
AとBの合計量を求める
ヒントになるのは、AとBを混ぜたあとに「水100gが蒸発し、濃度が12%から14%になった」ことです。食塩水の濃度は(食塩の量)÷(食塩水の量)×100で求められるので、食塩の量が同じであるかぎり濃度は食塩水の量に反比例します。したがって、濃度が14÷12=6分の7倍になったのなら、食塩水の量自体は7分の6倍になっていることがわかるのです。
蒸発の前後において食塩水の量の比が7:6であり、その差が100gであることから、蒸発前の食塩水の量は700g(蒸発後は600g)だとわかります。これで、AとBを混ぜたあとの食塩水の量を求めることができました。
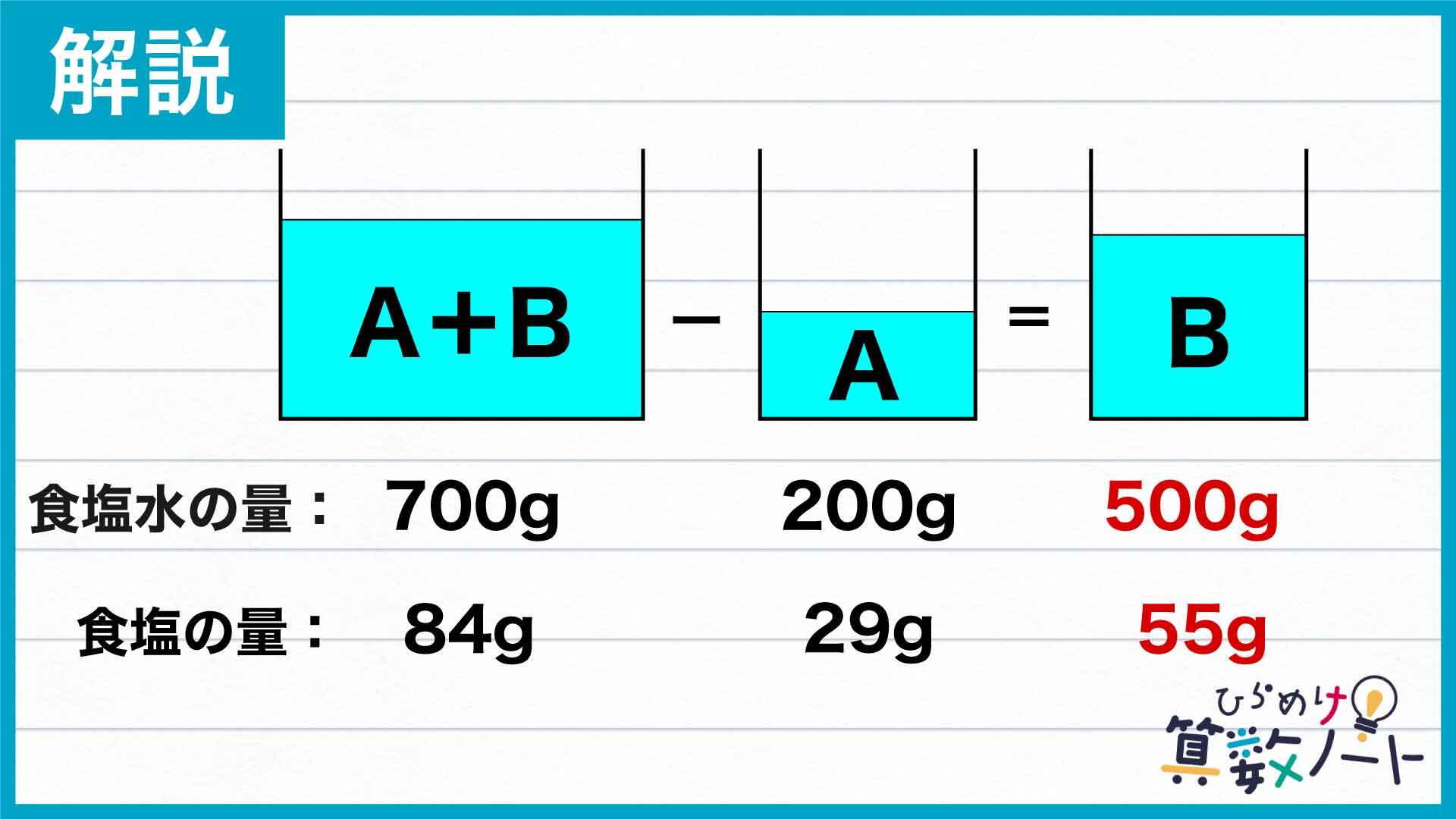
食塩の量を計算し、Bの濃度を求める
Bの濃度を求めるために、もう一つ欠かせない情報があります。それはズバリ、「食塩の量」です。AとBを混ぜたあとの食塩の量、およびAのみの食塩の量を求めることで、Bに入っている食塩の量を計算することができます。
食塩水に入っている食塩の量は、(食塩水の量)×(食塩水の濃度)÷100で求められるので、AとBを混ぜた場合の食塩の量は700×12÷100=84g、Aのみの食塩の量は200×14.5÷100=29gです。
AとBを混ぜた食塩水、およびA単体についての情報が出揃いました。これによって、Bの量とBに含まれる食塩の量をそれぞれ引き算で計算することができます。
B全体の量は700-200=500g、Bに含まれる食塩の量は84-29=55gです。したがって、Bの濃度は55÷500×100=11%であるとわかるのです。
答え:11%
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】













.jpg)







.jpg)







