解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ：【解答フォーム】自力で解きたい方はこちらへ！ 以下は問題の答えです。
今回の問題の解き方をまとめた図がこちらです。ポイントは補助線を引いてできた直角三角形の性質に注目することです。
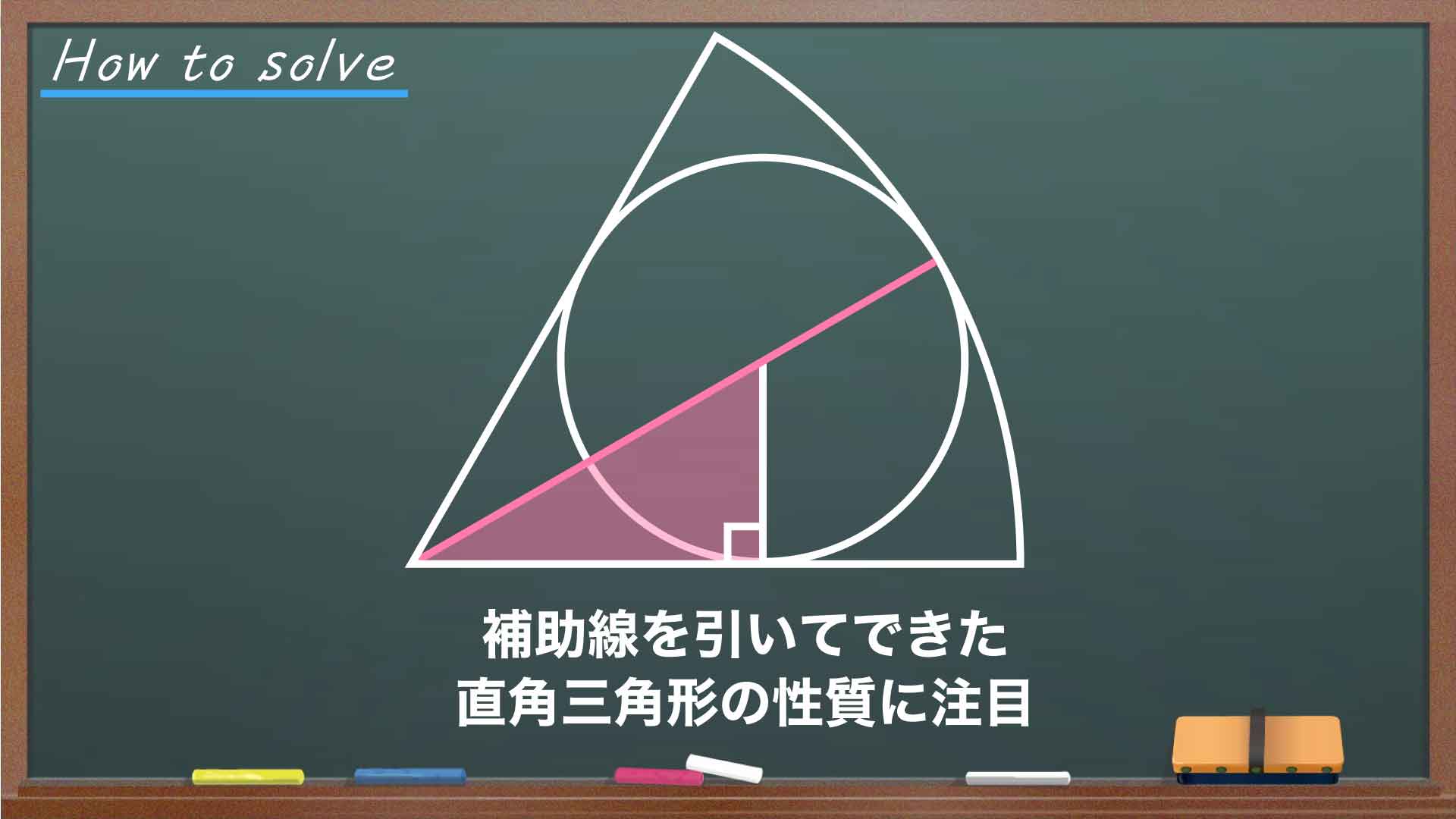
補助線を引いて直角三角形を見つける
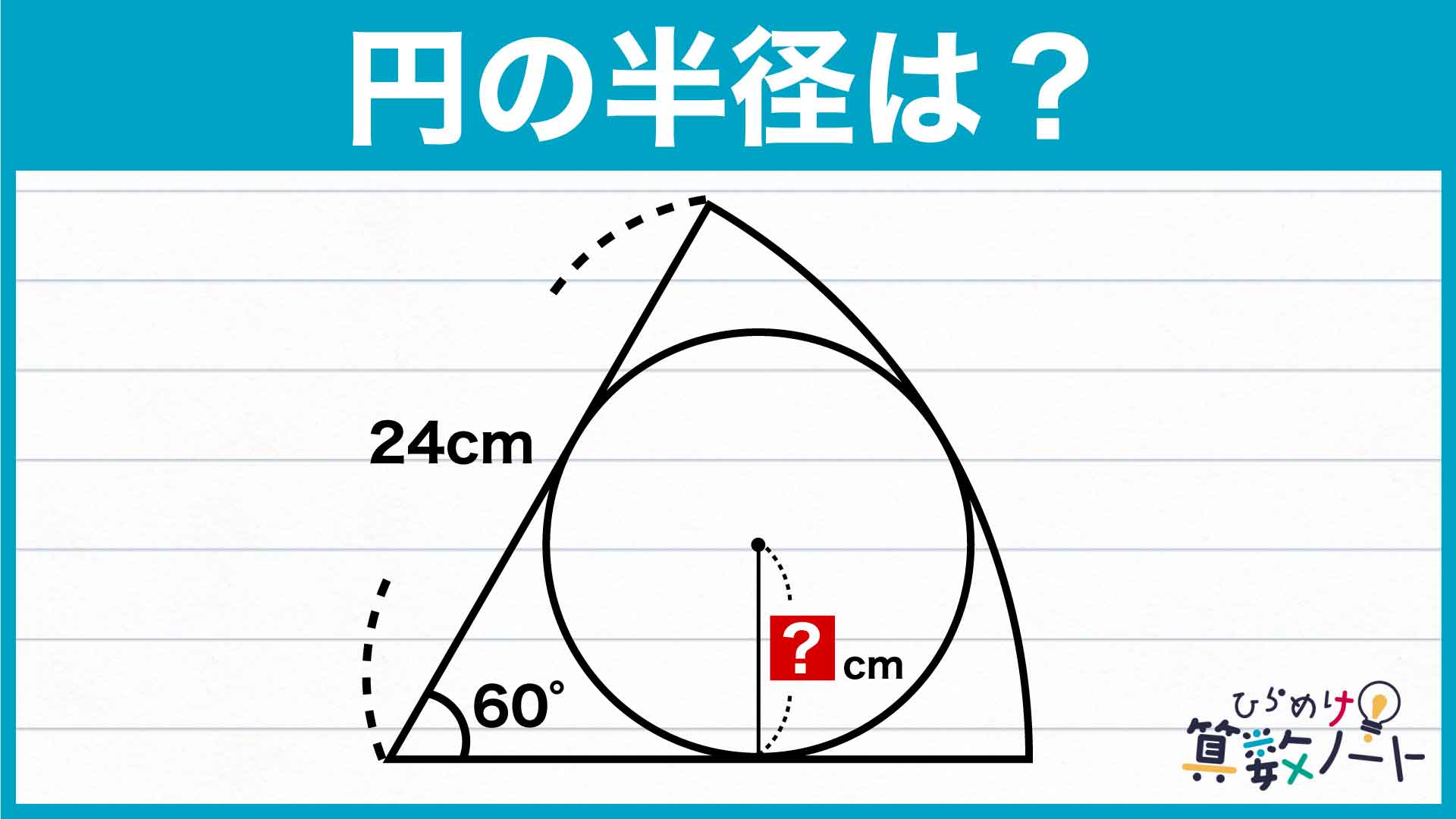
まずは、扇形の中心を点O、扇形の内部にある円の中心を点A、直線OAと扇形の弧の交点を点B、円と扇形が接している点のひとつを点Cとします。
このとき、線分ACは円の半径にあたり、扇形の半径と垂直に交わるため、三角形AOCは直角三角形となります。
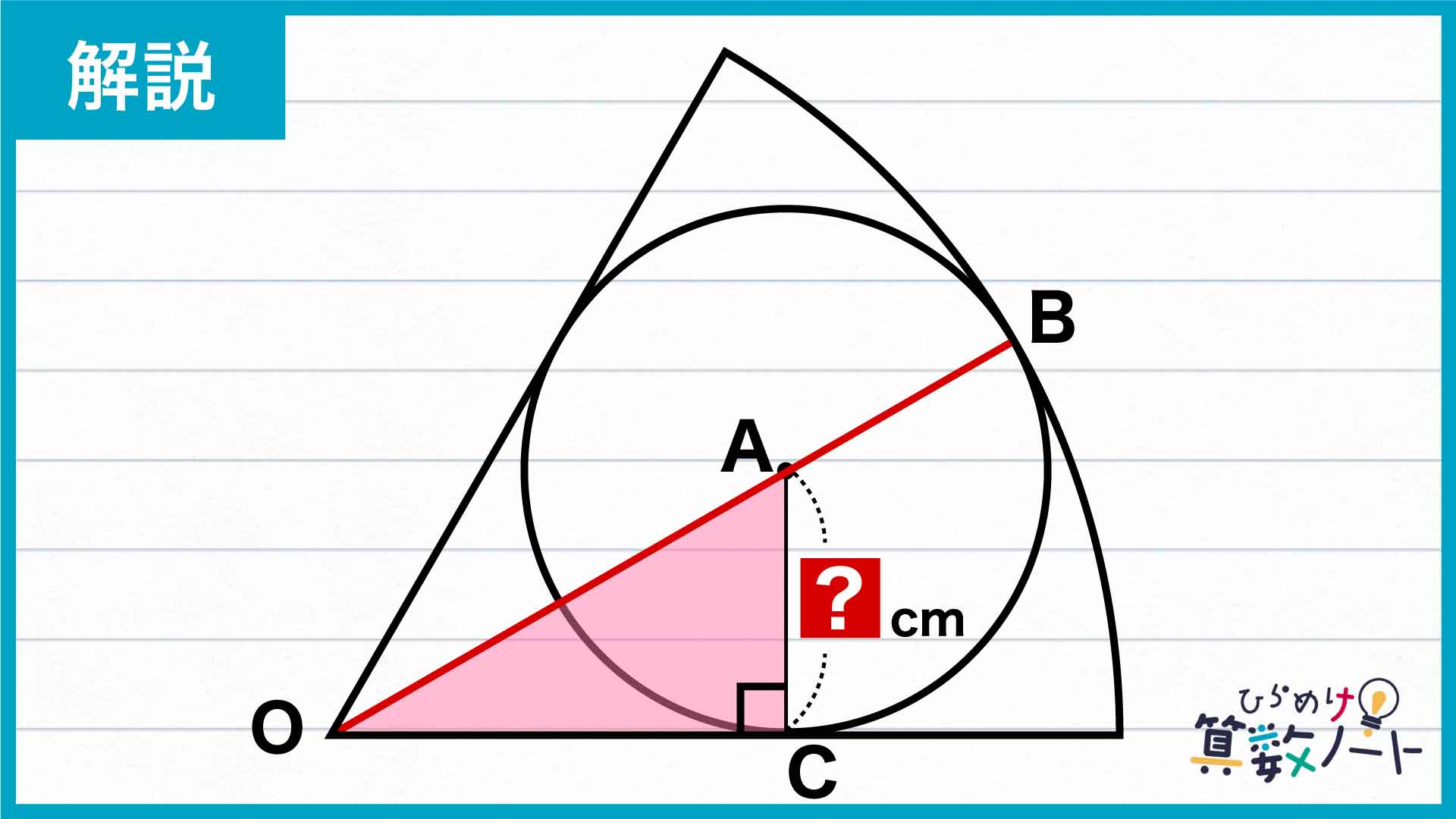
直角三角形AOCの性質は？
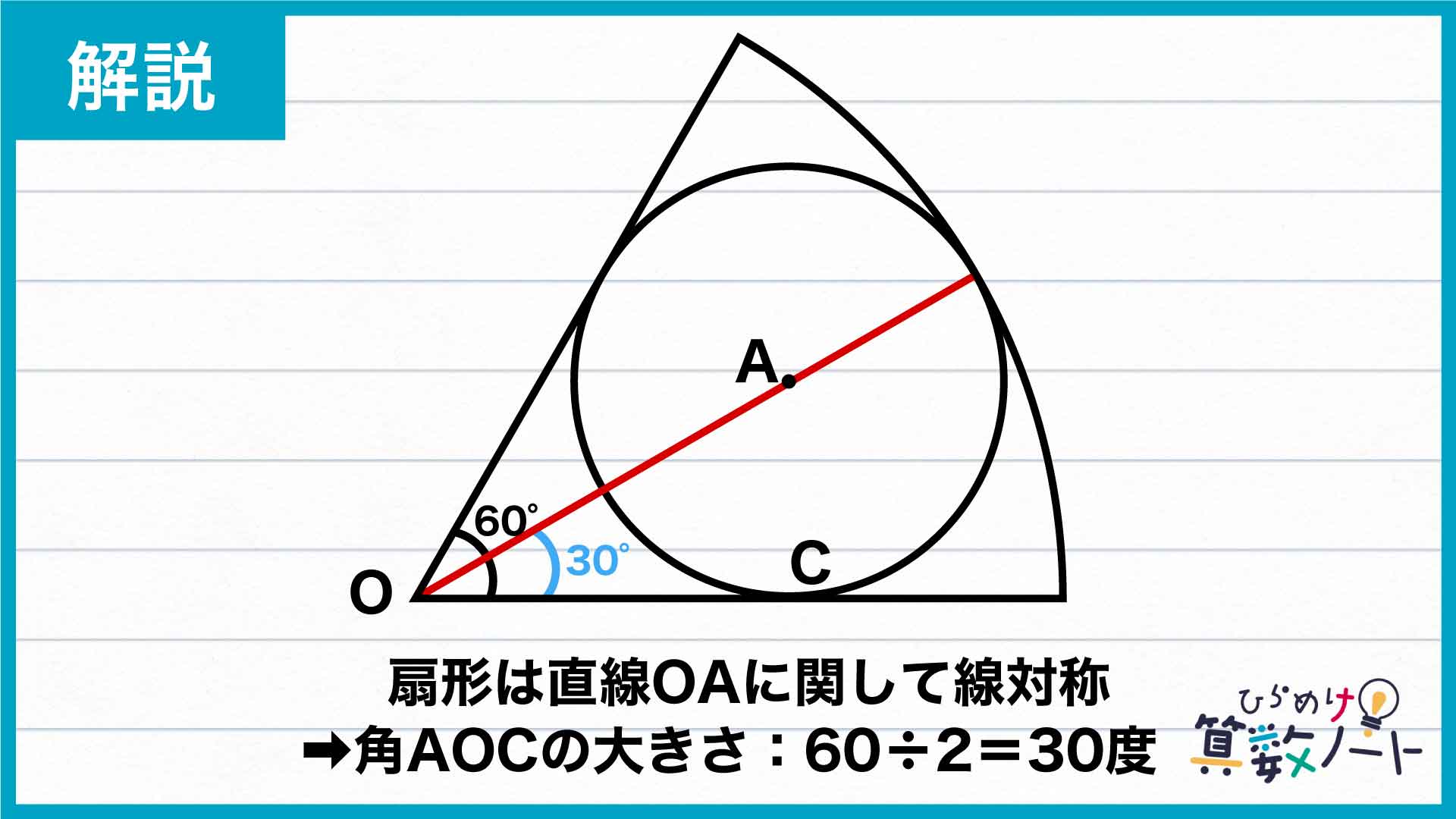
扇形は直線OAに関して線対称です。
したがって、角AOCは扇形の中心角の半分で、その大きさは60÷2=30度となります。
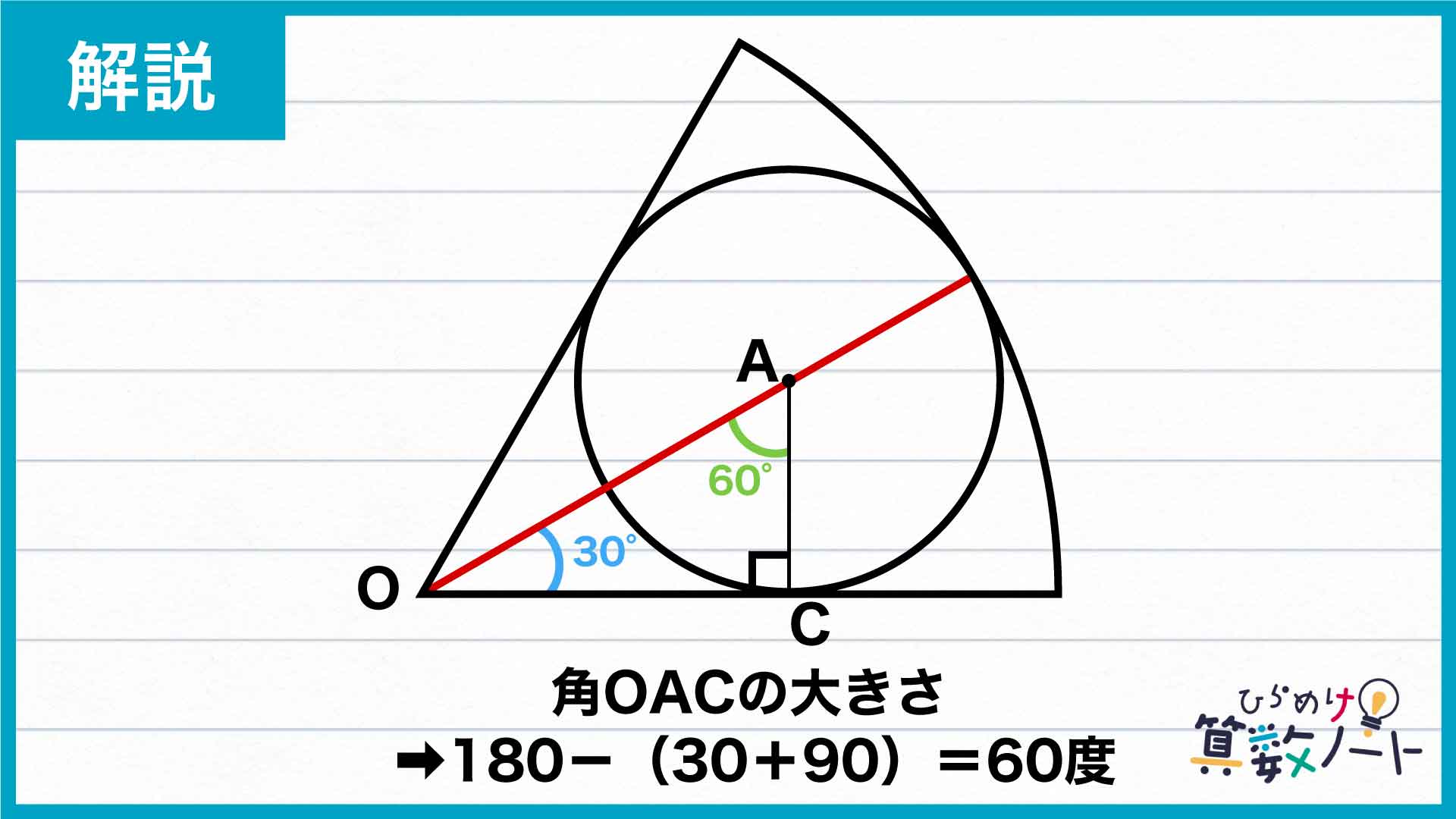
ここで直角三角形AOCに注目すると、三角形の内角の和が180度であることから、角OAC=180-(30+90)=60度であることがわかります。
3つの角が、30度、60度、90度である直角三角形を下の図のように2つ組み合わせると、三角形の3つの角がすべて60度になることから、正三角形ができあがります。
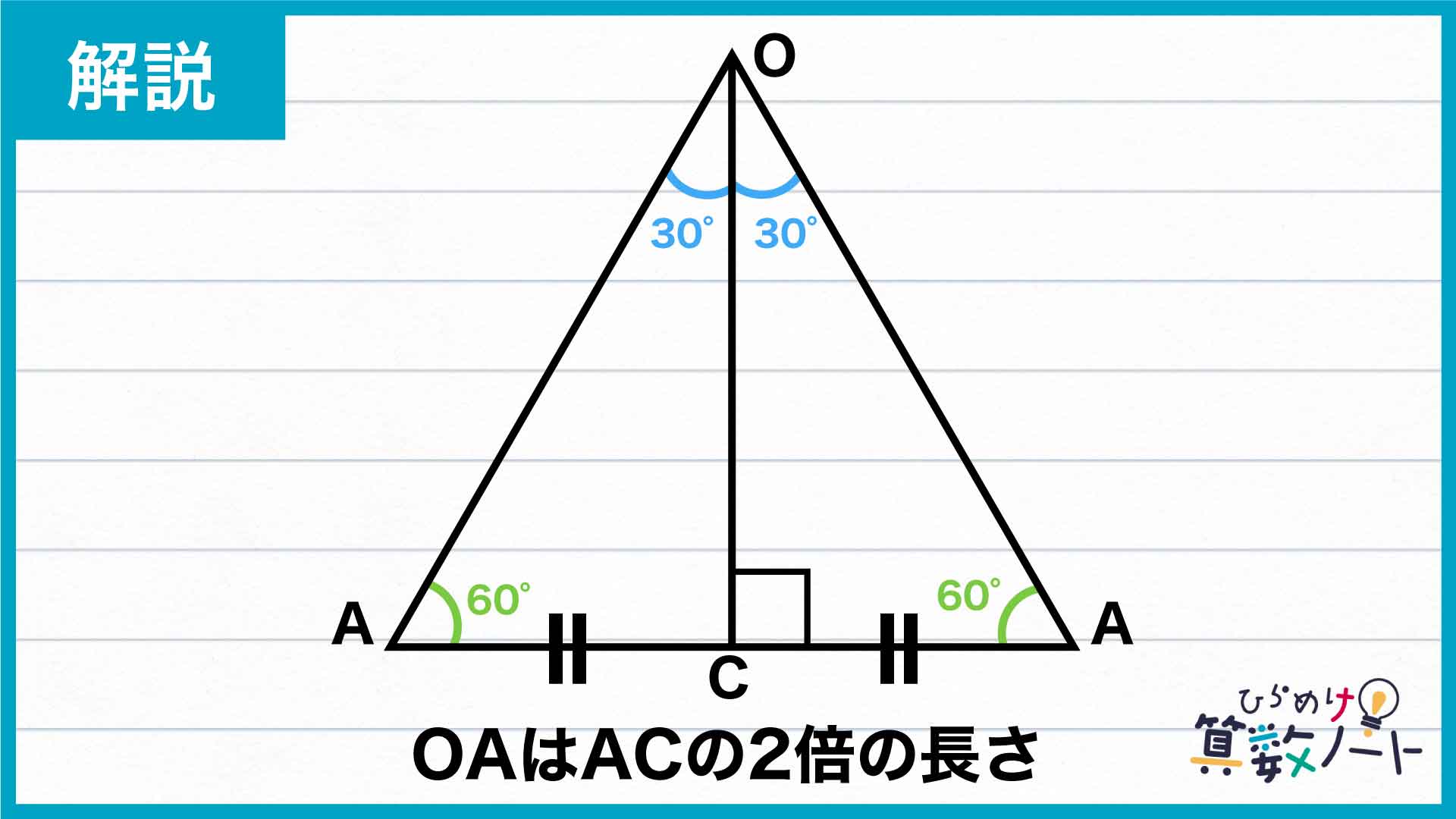
OAは正三角形の1辺であり、ACは正三角形の1辺の半分であることから、OAはACの2倍の長さであることがわかりました。
扇形の半径は円の半径の何倍？
扇形の半径OBは、OAとABの長さを足し合わせて求められます。
OAはAC（=円の半径）の2倍であり、ABは円の半径そのものであることから、OBは円の半径の2+1=3倍の長さです。
したがって、円の半径は扇形の半径の1/3であることから、24÷3=8cmとなります。
答え：8cm
「ひらめけ！算数ノート」のバックナンバーはこちら！
【前回の算数ノートはこちら】
【あわせて読みたい】
