コジマです。
選挙の度、私はあることを思うのである。
それは開票開始の瞬間。全国で開票が始まってものの数分で各地の候補者に「当確」、すなわち当選確実の報が出るのを見ては「いやいや早すぎでしょ？」となる。
当然、5分そこらで数万とある票を全て確認できるわけはない。それでもなお「○○さんが当選確実です！」と言い張れる理屈は何なのか。
誰かの勘で決めているわけでも、下馬評が高かったから……でもなく、そこにはれっきとした裏付けがある。
当選が確実ということは、ある候補者への票が過半数を占めることが確実、ということ。
具体的に、全体での得票率が60％だったとしよう。票が全部で1000票投じられたとすれば、その候補者への票は600票入っている。過半数を超えているので、もちろん当選である。
さてここで、「”全ての票がしっかり混ざっていて”、ランダムに100票を調べれば、57票なのか62票なのかは分からないが「およそ60票（100票の60％）」になるはず」というのは直感的に分かるだろう。
一方、10票調べたら、一番ありそうな6票以外にも、5票だったり7票だったりになる可能性が高いだろう。10票を見ただけでも全数での値に近づくことはできるが、割合的には50％や70％に振れうる。
すなわち、 ・「開いて調べた割合」は「真の得票率」に近く、 ・そのブレ（大きく外れる確率）は開く票が増えるほど小さくなる。
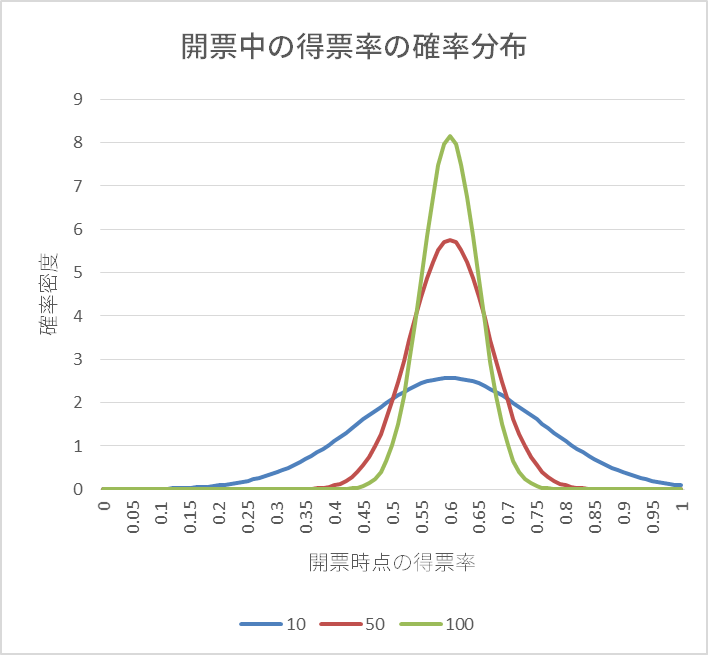本当の得票率を60％としたとき、10票、50票、100票開けた時点での得票率の確率分布。確率なのに1を超える理由は高校数学の範囲を超えるので割愛これを曲線で表すとこんな感じ。見方を説明しよう。 まず、先程述べた1000票中600票という前提を思い浮かべてほしい。この真実に、なるべく少ない開票数でたどり着くことが今回の目的だ。
例えば、開票した時に見える得票率が40％である確率は、10票開けたときにはそこそこに高いが、50票開けるとその半分以下となり、100票開ければほとんどゼロとなる。 1000票すべてを開ければ、得票数はかならず600となり、得票率は60％だ。
すなわちこの図では、票を開ければ開けるほど、その時点で開けた票の中での得票率が、真の値である60％に近づいていくことを示している。
何票か開けてみたときの得票率を横軸、その得票率になる確率を縦軸にとったとき、投票総数が多い場合、グラフはきれいな山型を描くとされている（これを正規分布という）。
開ける票を増やせば増やすほど「本当の得票率」になる確率が上がり、大きく外れる確率が下がるという訳だ。
統計学ではこの正規分布を用いて確実さを測ることがよくある。今回の場合、「これ以上外れることは○○％ない」というラインを引き、そのラインが50％より高いとき当確とすればよい。
細かい計算過程は記事の下部に記すので、気になるかたはそちらを見てほしい。ここでは大まかな流れを先に説明することにする。
今ここで、「これ以上外れることは97.5％ない」というラインを求めることにしよう。
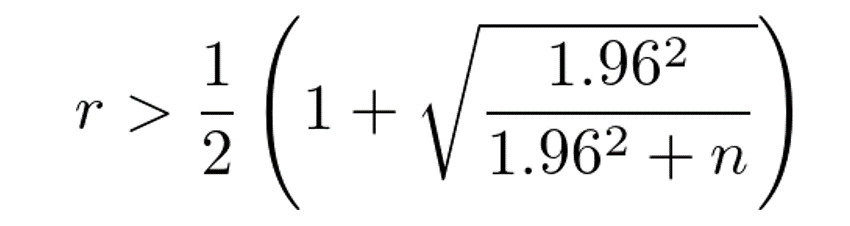
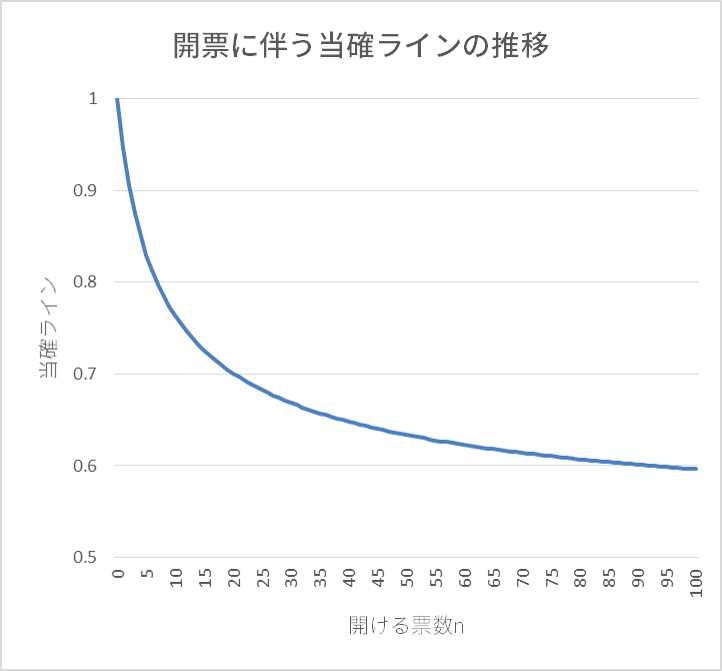横軸がn（開けた票）、縦軸がr（途中の得票数）。nが大きいほど判定ラインが下がる上の図は、97.5％の確率で「当確」と言えるようになるラインを、オープンする票数とその中での得票率の対応で描いたものである。
例えば、100票開けたときに60票がAさんの票であれば、Aさんは97.5％の確率で過半数の支持を集め、当確となる。
面白いのは、票の総数が1万だろうが10万だろうが、100票開けて60票取っていれば当確がつくところ。
開票者が10人なら、1人あたり10票見れば100票開けられる。開始数分で当確が出る訳である。
当確を出すのは各報道機関なので、実際この判定基準が使われているかは分からない。ただ、大まかな理屈は同じのはずだ。
今回の選挙で当確が出たときは、得票率とこの記事を読み比べてみてほしい。
※細かい統計学的説明
具体的に、「95％ない」ラインでやってみる。「本当の得票率」をR、「n票開けた時点の得票率」をrとすると、Rは次のような範囲に95％納まる（これより大きく/小さくなる確率はそれぞれ2.5％しかない）。
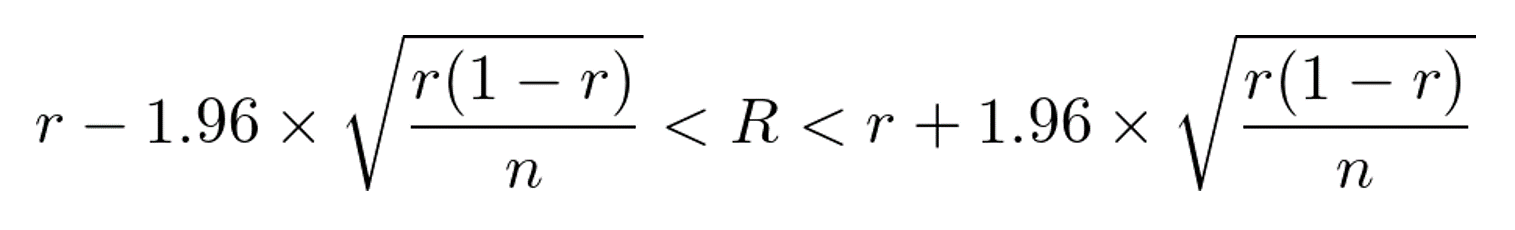
「1.96」という数字は正規分布の性質による。この範囲の下限についてみれば、これが50％より高ければ当確だから
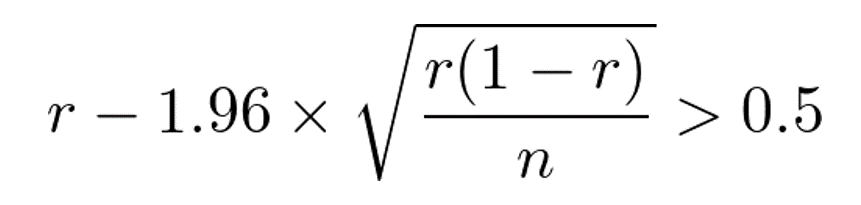
rがこの条件を満たせば当確だ。これを整理すると、rのnについての条件は上の図のようになる。
※上の図が95％ではなく97.5％となるのは、本当の得票率Rが範囲より大きい側にブレることは、当確を出すにあたって問題ないからである。
