Q.1:次の式を計算するといくつ?
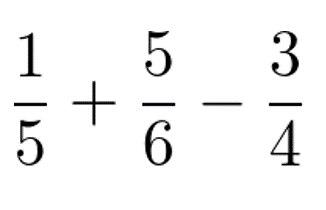
この式を単純に前から順に計算すると、次のようになります。
1/5 + 5/6 = 6/30 + 25/30 = 31/30
31/30 - 3/4 = 62/60 - 45/60 = 17/60(答え)
しかし、これでは分子の数が大きくなってしまい、通分が大変です。
そこで、後ろの引き算から先に計算してみると、次のようになります。
5/6 - 3/4 = 10/12 - 9/12 = 1/12
1/5+1/12 = 12/60 + 5/60 = 17/60(答え)
こうすれば、途中式の分子の数が比較的小さくて済むため、計算しやすくなります。
複雑な計算をすればするほど間違いやすくなり、仮に正しい解答の導き方をしていても答えが合わなかったりします。少しでも「計算が大変だな……」と思ったときは、より簡単な方法を考えるようにしましょう。
「楽をしようとする」のは、あらゆる問題に取り組むときに大切な気の持ち方です。問題を作る側も楽に答えを出せるような設定にすることが多いので、複雑な計算が必要に見える問題でも、少し立ち止まって考えてみると意外と楽に解けてしまうでしょう。
Q.2:A君は16日で、B君は20日で終わらせられる仕事があります。この仕事を2人で行ったとき、終わるのは何日後?
いわゆる「仕事算」と呼ばれる問題ですが、「仕事」の量をどう表していいかわからずとっつきにくいかと思います。
どう表していいかわからないときは、適当な数を仕事の量としてしまいましょう。「1」でも「100万」でもよいです(雑に見えますが、算数の問題はそれで解けるようにできています)。
今回は仕事の量を80(16と20の最小公倍数)としてみましょう。
すると、A君は仕事を16日で終わらせるので、1日に進む仕事の量は80÷16=5。B君の場合は80÷20=4となります。仕事の量を最小公倍数としたのは、割り算の答えが整数となって便利なためです。
2人で力を合わせると、1日に進む仕事は5+4=9となるので、80の仕事を終わらせるには9日あればよい(9×9日=81)ことになります。
Q.3:3つの正方形からなるこの図形の面積はいくつ?
青い大きな正方形の一辺の長さがわかれば他の2つの正方形の一辺の長さも求められますが、それには少し工夫が必要です。
3つの正方形の一辺の長さの合計は25cmになっているので、次の図のように考えてみましょう。
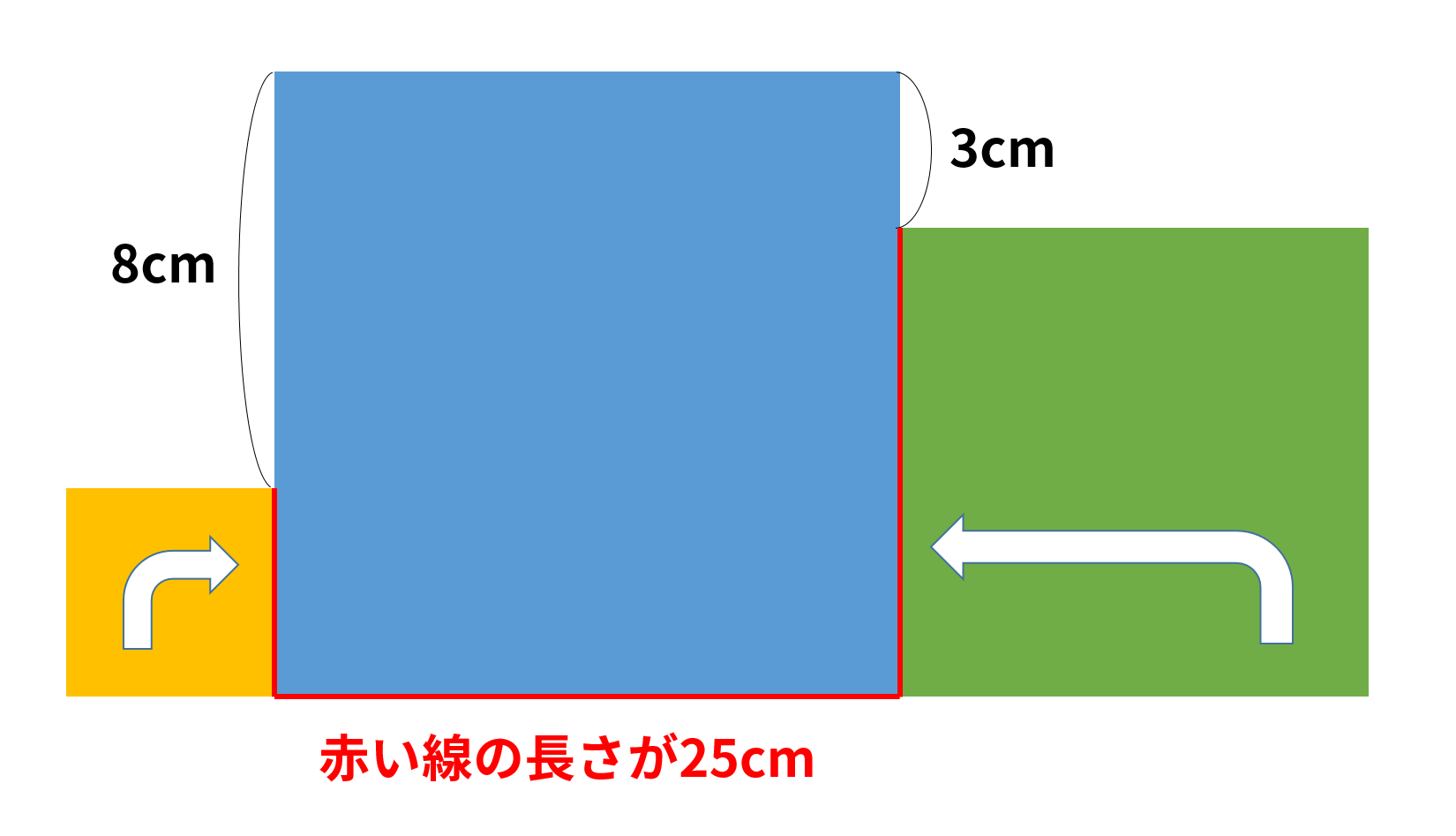
こうすると、青い正方形の3辺の長さの合計が8+25+3=36cmとなることがわかるので、一辺の長さは36cm÷3=12cm となります。
したがって、黄色の正方形の一辺の長さは12-8=4cm、緑色の正方形の一辺の長さは12-3=9cmとわかります。
3つの正方形の面積は合わせて4×4+12×12+9×9=16+144+81=241cm2です。
Q.4:1から100までの整数をすべて足すと5050。ではその中に含まれる「奇数」だけをすべて足すといくつになる?
このような数の和を求める問題は、単純に1+3+5+……と足していくと計算にとても時間がかかるうえに、答えが出せても数が大きすぎて合っているかわかりません。
そこで、問題文に書かれている情報を活用しましょう。問題を解くうえでのヒントとして書かれていることが多いので、これを使わない手はありません。今回の問題だと、「1から100までの整数をすべて足すと5050」という情報が使えそうです。
1から100までの整数のなかに、奇数と偶数は50個ずつあります。それなら5050の半分で2525……かと思いきや、そうではありません。次の図のように、偶数の和の方が50だけ大きくなります。
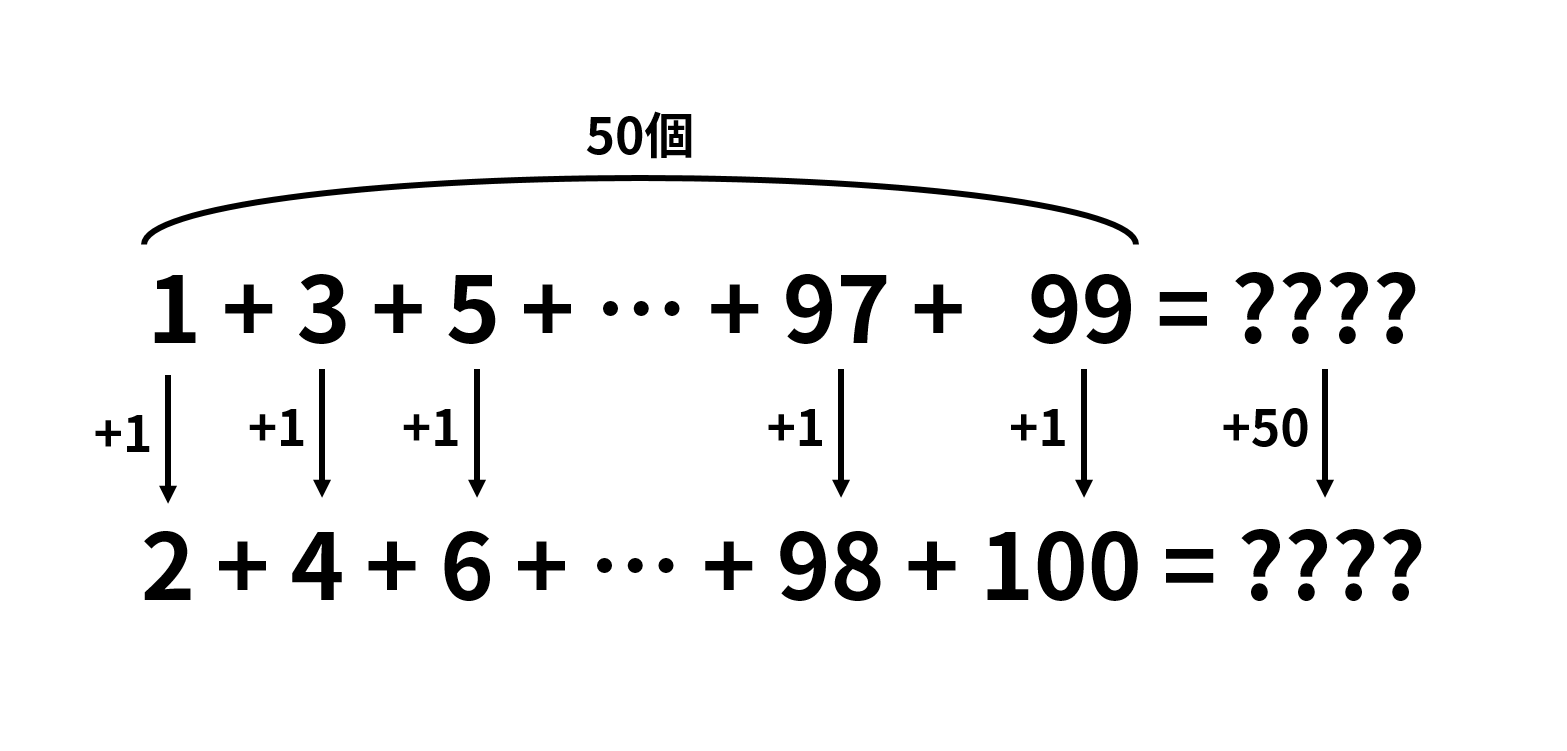
奇数の和を2500にすれば、偶数の和は2550となり、ふたつを足し合わせると5050で計算が合います。
ちなみに、1から100までの整数の和が5050であることは、次の図のような考え方をすると101×50で求められます。奇数だけの場合でも同じような考え方が可能です。
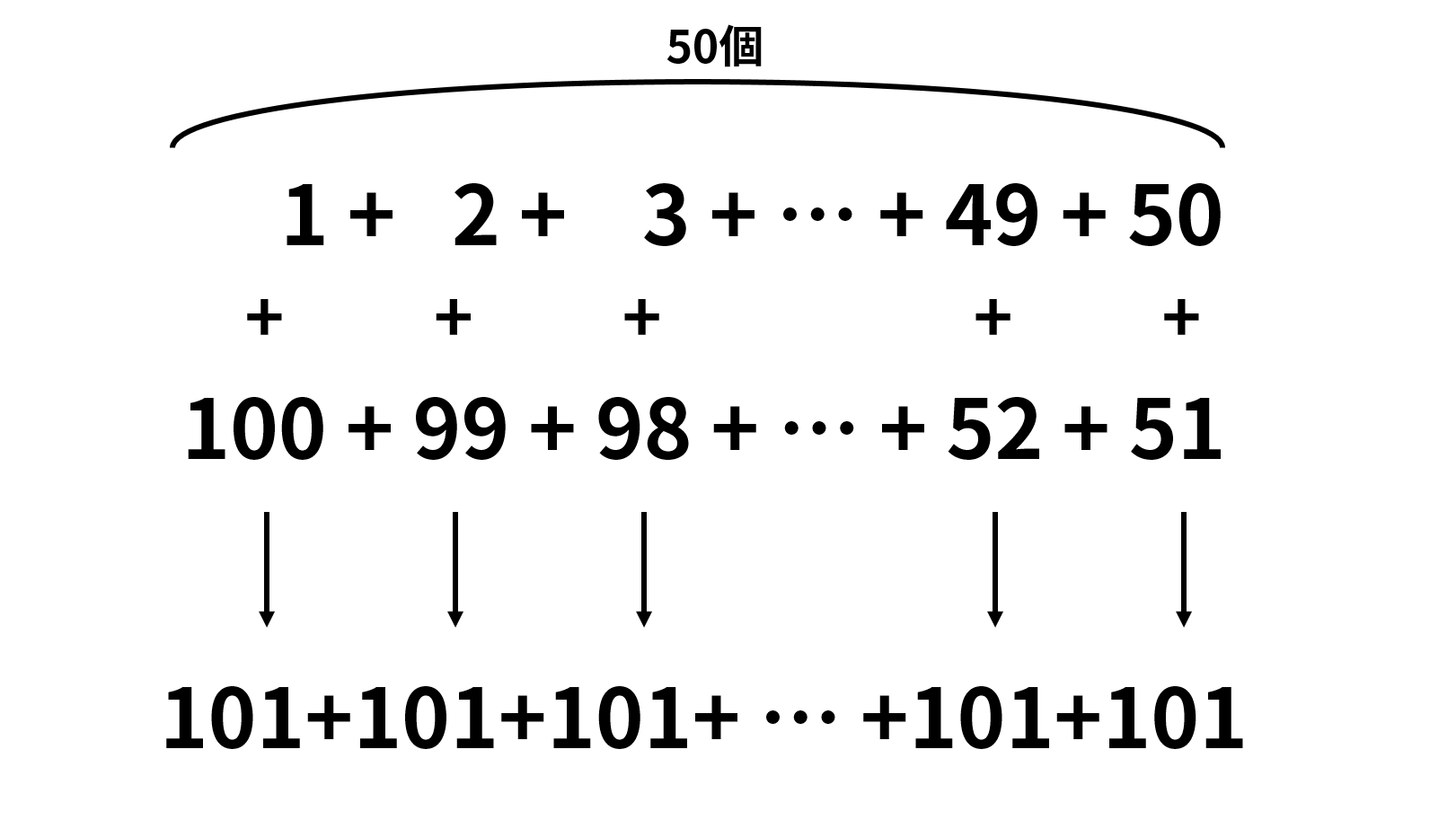
問題を解くうえで一見関係なさそうな情報が問題を解く糸口になっていることがあるので、問題文は隅々まで読むことをおすすめします。
Q.5:片道60kmの道のりを、行きは時速20km、帰りは時速12kmで進みました。行き帰りの平均時速は何km?
「時速20kmと時速12kmだから、平均して(20+12)÷2=32÷2=16!」と考えたあなた、残念!
正しく考えるためには「平均の速さ」の定義がどういうものかを確認しましょう。「定義」とは「定められた言葉の意味」のこと。算数・数学で用いられる言葉は、基本的に何らかの定義がなされています。。
平均の速さの定義は、移動した距離÷かかった時間です。
この問題は、片道60kmなので、行きにかかった時間は60÷20 = 3時間、帰りにかかった時間は60÷12=5時間。よって、かかった時間は8時間となります。また、移動した距離は60kmの往復なので、60×2=120kmです。
これを定義の式に当てはめると120÷8=15となり、行き帰りの平均の速さは時速15kmとわかります。
「速さの定義なんて簡単だ!」と思いがちですが、慣れてきたときに今回のような平均速度の問題を出されると間違えてしまいます。
問題が複雑になったときこそ基本に立ち返り、定義に出てくる値一つひとつ(「移動した距離」や「かかった時間」など)に正しい値をあてはめることを意識しましょう。
これは高校や大学でよりレベルの高い勉強をする際にも重要なことです。
まとめ
ここまで解き方のコツをいくつか述べましたが、最後にものをいうのは問題を解いた量だと思います。たくさん問題を解くとある程度パターンが見えてきて、問題を見た瞬間に「まずはこうしよう」という糸口をつかめるようになるはずです。
この記事が、算数・数学に対する苦手意識の克服や成績アップの手助けに少しでもなれば幸いです。
【あわせて読みたい】










.jpg)