コジマです。
円周率が3.05より大きいことを証明せよ。
(東京大・2003)
東大の入試問題の中でも10本の指に入る有名な問題(※1)である。当時の「ゆとり教育では円周率は3だと教える」という風評(※2)も相まって世間に広まった。
※1 余談だが、個人的には『受験の神様』というドラマで成海璃子がスラスラ解いていた問題という印象が強い
※2 当然そんなことはなく、計算が複雑になる場合に円周率を3として計算する場合もある、くらいの事実が尾ヒレをつけて広まってしまった
さすが東大、こんなん解けねえや……とお思いのあなた。実はこの証明、中学生でもそれなりに理解できてしまうくらいシンプルなのだ。
円周率って何だっけ
とはいえ、「円周率が何か」を理解していなければ証明などできるはずもない。
円周率についての説明はQuizKnockに記事があるので、そちらをお読みいただきたいが……
辞書的な説明をすれば、円周率とは「円の円周と直径の比」である。直径が1の円であれば、その円周の長さがそのまま円周率になる。
「3より大きい」は超簡単!
つまり、直径1の円の円周が「何か長さが3.05より長いもの」より長いことを示せれば証明完了という訳だ。
この「何か」にはふつう、円に内接する正多角形の周を用いる。具体的に正六角形でやってみよう。
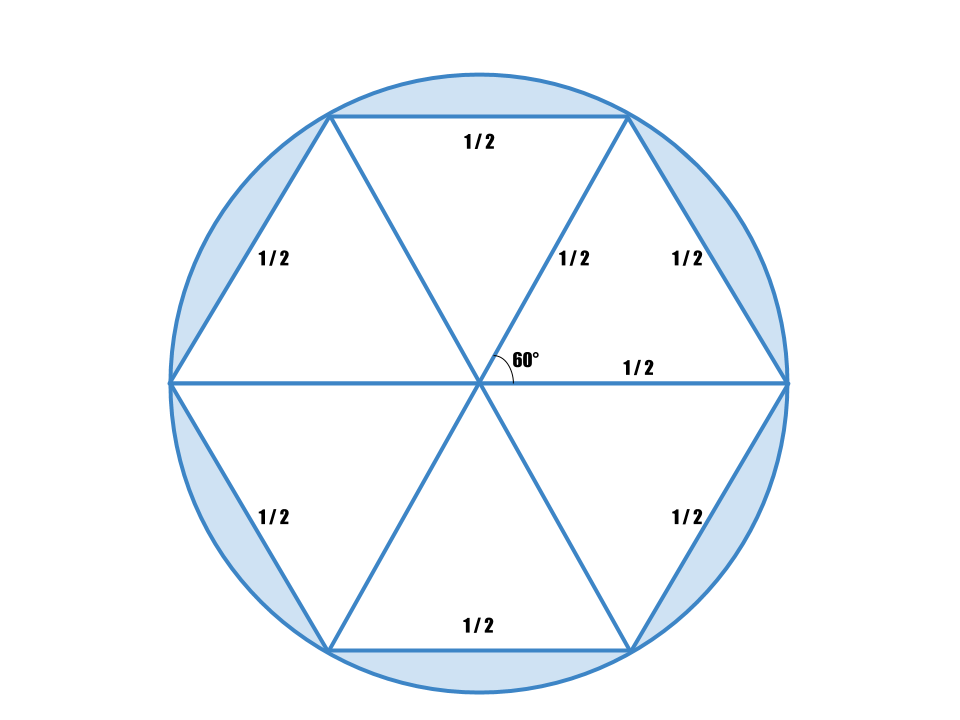
直径1(半径1/2)の円に内接する正六角形は、一辺の長さが1/2で、辺が6本あるので、その周の長さは3である。このことから、円周は3より長い⇔円周率は3より大きい、ということが導ける。
そう、ここまでの説明だけで「円周率が3より大きいことを証明せよ。」という問題は解けてしまったのだ。
「3.05より」はそれなりに大変
「3より」を「3.05より」にするためには、内接する正n角形の周を3.05より大きくすれば、要するにnを大きくすればよい。ただし、問題は手計算で解かなければいけないので、周の長さが求められる正n角形にしなければいけない。同時に、nをケチって小さくすると3.05より大きいことが示しづらくなるので、ある程度は大きいnを使いたい。
そこで、正12角形でやってみることにする。6の倍ならいけるやろ。
まず、半径1/2の円に内接する正12角形の一辺の長さを求める。円の中心と正12角形の隣り合う2頂点がなす三角形は、頂角の大きさが30°、2辺の長さが1/2の二等辺三角形。
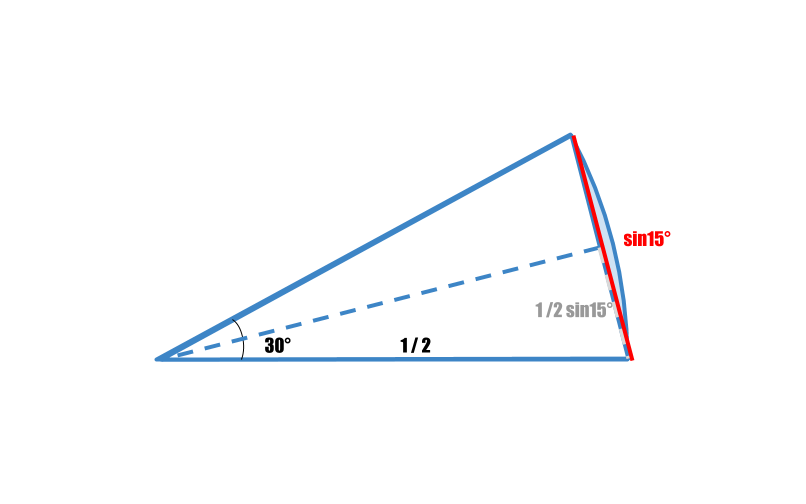
残りの1辺は三角関数を使えば求められる。二等辺三角形の頂点から垂線(上図の点線)を下ろすと、斜辺が1/2、1つの角が15°の直角三角形になるから、底辺の半分の長さが1/2×sin15°。つまり底辺の長さはsin15°となる。
sin15°
=√{(1-cos30°)/2}(半角の公式)
=1/2×√(2-√3)。
この長さの辺が12本あるので、正12角形の周の長さは6√(2-√3)だ。

これが3.05より長いことを示せばいいのだが、そこは東大。すぐに答えには辿り着かない。
というのも、√(2-√3)は√の中に√があり、厳密にいくつより大きい、というのを計算するのが面倒なのだ。
まず、√3=1.732...なので、√3<1.74。
よって、2-√3>0.26。
ここで、最終的に6√(2-√3)>3.05が出せればいいことを思い出す。不等式の両辺を6で割れば√(2-√3)>0.5083...。
0.5083より少し大きい0.509は、2乗すると0.259081(※3)なので、2-√3>0.26>0.5092という不等式が作れる。
※3 0.512=0.2601だと本当にちょっとだけ0.26を上回ってしまう。√3<1.733としておけば2-√3>0.267で大丈夫だったが……
両辺の平方根をとれば√(2-√3)>0.509。両辺に6をかけて6√(2-√3)>3.054>3.05となり、証明完了!


ね、簡単でしょ?
と思えるのは解説を読んでいるからで、初見だったり何も見ないで自力で解いたりするとやっぱり難しいのである。
ぜひ1週間後くらいに自力で証明してみてほしい。










.jpg)