さあ証明しよう 間違いのないように
まず、1人だけ生きた年代が違うピタゴラスの存在について考えよう。ピタゴラスへのお願いは「確かめさせて」。フェルマーほどではないが比較すると弱めだ。
ここから察するに、ピタゴラスにはあくまで確認に留める程度の内容を問うただけなのだろう。数学の基礎を作った男だが、それはあくまで2500年前のこと。となると、基本的なことをピタゴラスに確認した上で、より高度な証明へと進んだのではないかと推測できる。
ピタゴラスも気づけば彼方―――、活躍時期の近い本命の3人についても年代を整理したい。
フェルマーが活躍したのは17世紀。オイラーが生まれたのはフェルマー誕生のちょうど100年後、18世紀のことである。リーマンの活躍時期は19世紀だ。つまりは、フェルマーが一番のパイセンなのである。
パイセンであるということは、より基礎的な内容を研究していたと考えられる。
となると、フェルマーが扱っており、かつオイラーやリーマンが発展させた分野なら、わざわざフェルマーまで遡る必要はない。質問したという事実だけ作っとけば先輩の顔は立つよね。
恋のベン図に潜む禁断の領域、それは3人の研究分野の積集合だ。最適解はもうすぐそこである。
とはいえ、まだ高いハードルが残っている。クイズ王たる私も、大学レベルの数学は苦手分野だ。頭がちっとも追いつかない。
やはり、学問のことはその道の人に聞くべきだろう。
知り合いの数学に詳しい人を召喚だ。
▲QuizKnockが誇る数学者
いま、ふたりなら実証できそう
有名な未解決問題のリーマン予想も、オイラーが考案し、リーマンが発展させたこのゼータ関数に関わってきます。
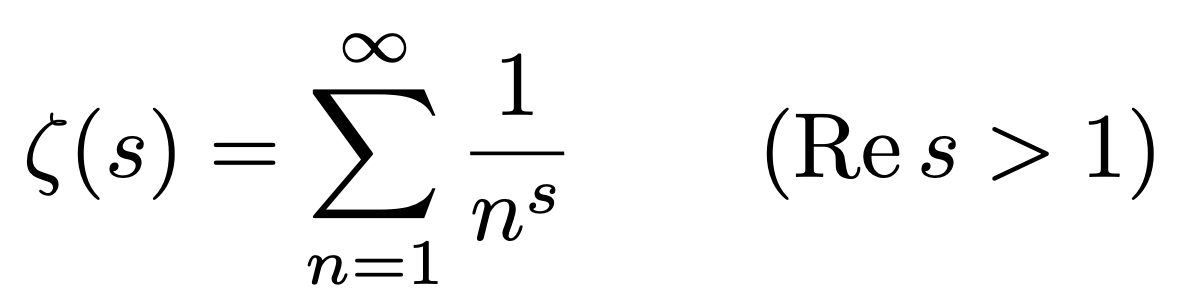▲「リーマン予想」に関わるリーマンゼータ関数ζは、上記の等式で定められる関数を複素平面上に解析接続して得られる有理型関数（詳しくはこちらの記事のQ6をどうぞ）
よかった、さすがフェルマー先輩っす。未来の研究を目にしてさぞ驚いただろうが、意志を継ぐ後進を喜んでもくれるんじゃないだろうか。
▲たぶんこうなる
答えはもうすぐそこ
ゼータ関数でつながるオイラーとリーマン、ふたりが恋のキューピッドだ。彼らについて、もう少し解像度をあげよう。
歌詞では、オイラーには「なんでか教えて」、リーマンには「確かにさせて」と依頼している。前者に対しては自ら理解しようという気があるが、後者はもはや作業を投げているのだ。となると、恋を描く数式の本丸はリーマンの研究結果にあるだろう。リーマン先輩、今日も徹夜っすね……。
▲リーマン先輩、おねがいします！
ゼータ関数におけるオイラーとリーマンの違いを述べるならば、リーマンはオイラーの用いた関数に「複素数」を導入していることだ。複素数とは、実数と虚数を組み合わせた数。虚数というイマジナリーな存在を導入することで、リーマンはより精緻な描写を可能としたのだ。
実部と、そこに加えられた虚部。それこそが、偉大な数学者たちの関心事であり、追い求め続けた恋の答えであった。
そうだ。答えはそこにある。
歌詞が描いていたのは、虚実入り交じるラブ・ゲーム。
つまり、駆け引きこそが、恋なのである！！！！ Q.E.D.！！！！！
……さて、多少エレファントな証明にはなったが、この世の未解決問題がまたひとつ過去のものとなった。
やはり、恋とは複雑怪奇。単純な足し算では解き明かせないものである。
なんてったって、恋は「かけ」「ひき」ってね！
お後がよろしいようで■
「伊沢拓司の低倍速プレイリスト」は伊沢に余程のことがない限り毎週木曜日に公開します。Twitterのハッシュタグ「#伊沢拓司の低倍速プレイリスト」で感想をお寄せください。次回もお楽しみに。
【前回はこちら】
【あわせて読みたい】
