「正解は正解！不正解は不正解、残念！」
――幼少期から算数や数学が好きで、「数学を捨ててやることがない」とも話していましたが、数学のどんなところにそんなに惹かれたのだと思いますか？
鶴崎 小学生の頃、数学が好きな理由として僕がよく言っていたのは、「答えが一つなんだけど、解き方はいくらでもある」というところですかね。
問題があります、で、答えがあります。そこはもう決まってるんですね。その問題からは一つの答えしか出ない。でも解き方は自由なんですよ。そこがなんか好きで。
▲身振り手振りを交えて語る鶴崎氏
――プロセスの自由さとバシッと答えが出ることが大事だったんですね。
鶴崎 そう、これはちょっと間違った見方かもしれないですけど、当時は国語の記述問題をやっても「結局答えはどれなんだよ」って思ってしまってたんですよ。そこの良し悪しも、何を目指したらいいかもわかんなくて、「どう書いてもいいって言われましても」みたいな（笑）。今はそんなことないですけどね。
▲「どう書いてもいい」という問題に困惑していたという鶴崎氏
鶴崎 だからそういう点では算数や数学は一つに答えが定まるのが好きだったんです。「これは解けた」っていうのが確実にわかるし、「解けてないかもしれん」みたいなのってなくって。「正解は正解！ 不正解は不正解、残念！」っていうのがはっきりわかって（笑）。
――でも解き方は一つじゃない、と。
鶴崎 数学には武器が色々あって使える。関数を使って解きましょうとか図形を使って解きましょうとか、整数の性質を使って解きましょうとか。「本質的に自由なんだけど、最後は答えが定まる」というのが、数学の非常に好きなところです。
厳密に言えば、それはある種間違っているんですけどね。数学の研究って必ずしも一つの真実に向かっているというわけではないので。それに国語だって答えが定まるものは定まるし、嘘と言えば嘘なんですけど、小学生の時はそういう感覚があったんです。
鶴崎氏が考える「最も美しい数式」とは？
――鶴崎さんの数学の美学を聞いたところで、鶴崎さんの考える「最も美しい数式」を教えてくれませんか？
鶴崎 これはねぇ、難しいですねぇ〜（笑）。
鶴崎 「最も美しいとかないよ！」って思ったりするんですけど、それでも、「ピタゴラスの定理」はいいかなと思ってて。
――ピタゴラスの定理！
鶴崎 ピタゴラスの定理ってご存知かもしれないけど、直角三角形で、直角を挟む辺をa,bとして、斜めの線をcをするとa×a+b×b=c×cになるという。
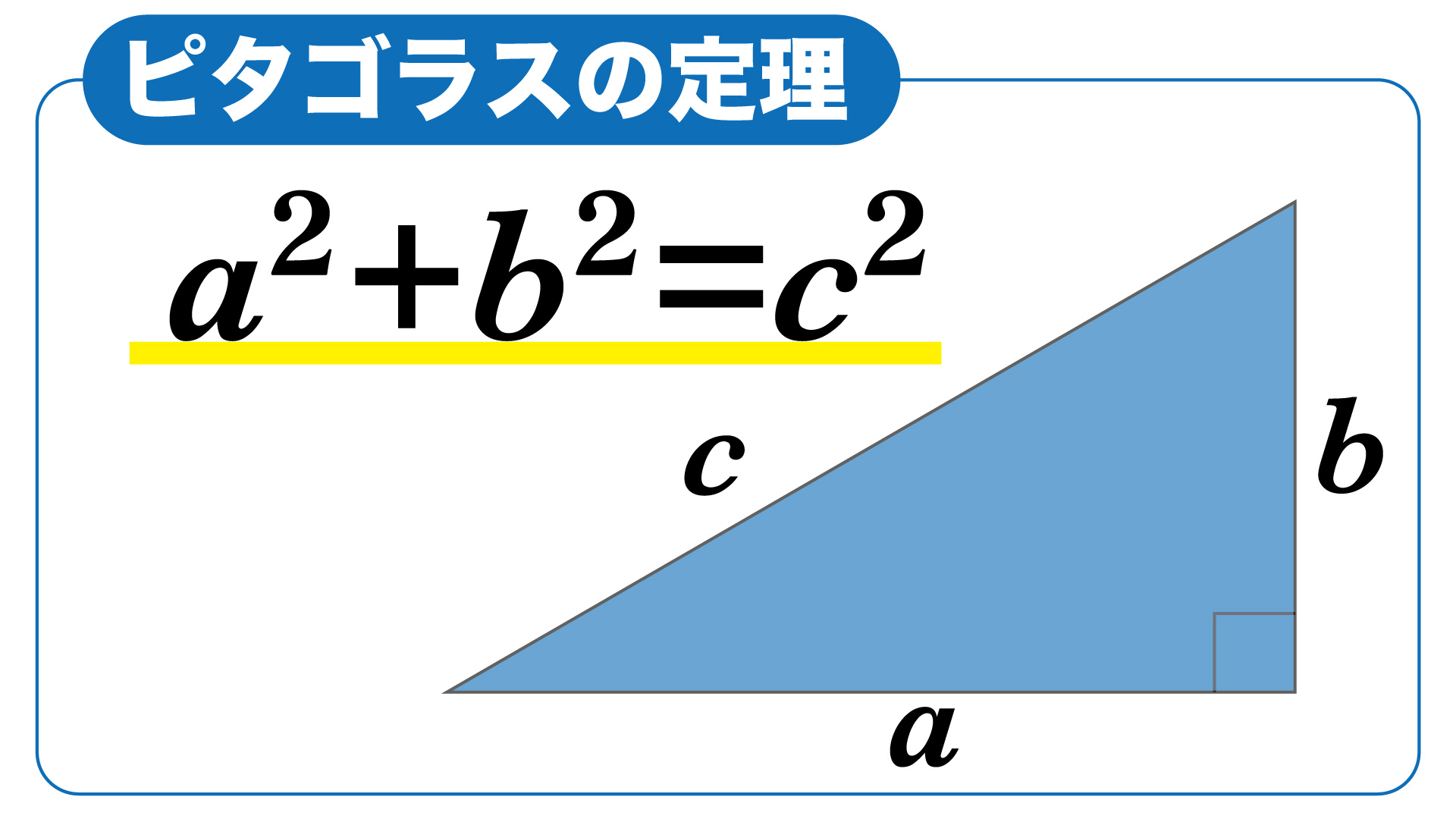▲ピタゴラスの定理！ やったことあるぞ！
鶴崎 でも、直角三角形を見ても絶対にこの数式を想像できないですよね。この辺とこの辺をかけて、この辺とこの辺をかけて足すと、この辺とこの辺をかけたのと同じって、「そんなわけないだろ！」「嘘だろ！」って思いますよねやっぱり（笑）。
――（笑）。
鶴崎 数学の面白さのひとつって、そういう予想外の結果が出てくることだと思うんですよ。
数学の理論って、結局みんなが納得しないといけないから、基本的に自明なもの、つまり「そりゃそうでしょ」と思えるものじゃないとダメなんですよ。
鶴崎 ダメなんだけど、結果として非自明な、「そんなの当たり前じゃないだろ！」「嘘だろ！」みたいな結果が出てくるものが結構美しいと言われますね。例えば、オイラーの等式とかは「そんなわけないじゃん！」感が強くて、美しいってよく言われますけど。
▲こっちはオイラーの等式
鶴崎 でも証明を聞くと、当たり前ですけど証明なんで、「そりゃそうだ」という理論で行われてるんですよね。
「ピタゴラスの定理」ってそういう定理として、学校教育で習う最初の数式なのかなと思いますね。
――言われてみれば確かに……。
鶴崎 そのうえピタゴラスの定理はめちゃくちゃ使われてるじゃないですか。ピタゴラスの定理を知らなかったら、コンピューター科学とか到底できないし地図とかも作れないし。
鶴崎 使い道がめちゃめちゃある、もちろん短くて綺麗・簡潔、なのに非自明。やっぱりピタゴラスは偉大ですね。
――ピタゴラスは偉大！
鶴崎 今はもはや空気のように使ってるから、今更いちいち美しいなって思ってるわけじゃないんですけど、改めてこの式は綺麗かなと思いますね。
――ありがとうございます。ピタゴラスの定理について、こんな風に考えたことがなかったです。正直、「全然知らない数式が出てきたらどうしよう」とは思っていましたが……。
鶴崎 いやまぁ、代数学の定理とかで綺麗なのもあるんですけどね。僕がよく研究で使ってる分野だと、「シューアの補題」っていうのがあるんです。
――え、えぇと……。
鶴崎 シューアっていう数学者がいて、補題っていうのは定理を示すためにつけられる補助的な命題のことです。もともとはある問題の準備として考えられて、それがかなり応用できるということで色々なところで使われていて、シューア補題はかなり美しいなと思うんですけど……。
――なるほど……。
鶴崎 説明するのは不可能ではないですけど非常に困難なので、まぁまぁ……。
――こ、これはまた別の機会に聞きましょうか。
鶴崎 そうですね（笑）。
今回のインタビューでは鶴崎さんと数学との出会いや、その美学などを聞いていきました。
次回は鶴崎さんが実際に大学院で研究している内容や、「何をやっているかわからない」と言われがちな数学の研究をはじめ、基礎的な分野を研究する意義などをインタビューしていきます。
【後編はこちら】
【あわせて読みたい】
