不可能であることを証明する！？
次に、nを3で割った余りが2のとき、すなわち0以上の整数mを用いてn=3m+2と書けるとき、条件を満たさないことを証明します。 つまり、〇を2,5,8,……個並べることができないということを示します。
実はここがこの問題で一番難しい部分です。解いたことがある方ならわかると思いますが、この辺りで解答を書く手がピタッと止まってしまいます。では、なぜ難しいのでしょうか？
「できる」ということを証明するときは、たくさんある〇の追加法のうち、1つでも具体的な方法を見つけられれば良いです。
しかし、「できない」ということを証明するときは、たくさんある〇の追加法のうち、どの方法でもできないということを言わなければなりません。〇の追加法を全通りやってみて、どの場合でも〇がn個並ばないことを確かめることができれば良いですが、今回は追加法が無数にあるため、この方法は使えません。
さらに、〇や●の数の変化を考えるだけではなかなかうまくいかないというのがこの問題の恐ろしいところ。では一体どうしたらいいのか……。
実は、次のアイデア1,2を用いるとうまくいくんです。
【アイデア1】四角いオセロの石を2つ用意し、最初は白い面を上に向けて両端に置く
考え方をシンプルにするために、四角いオセロの石を両端に置きます。
例えば、
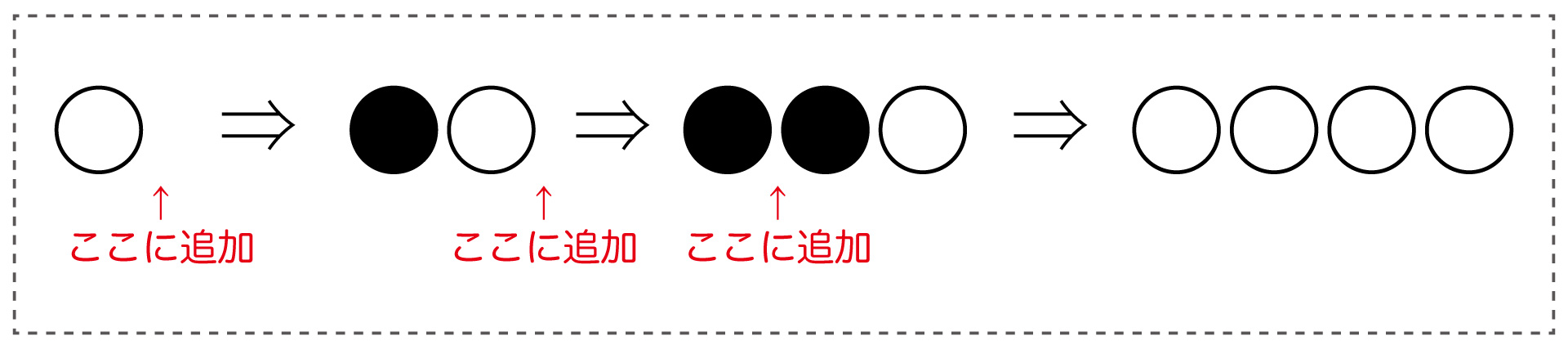
の両端に□を加えると、
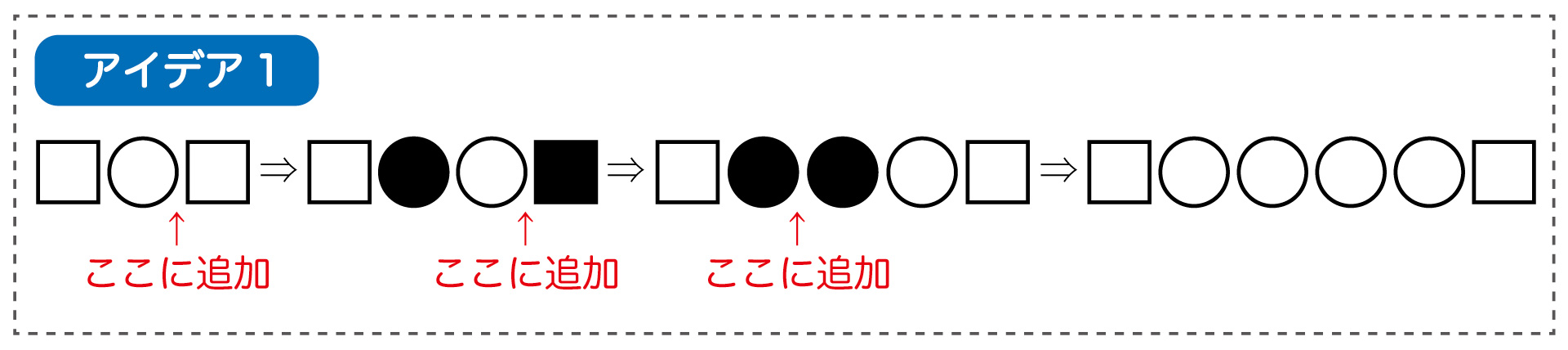
となります。両端の石を無視すれば、両者は一致します。
▲今までルール1だったものが、両端の石を追加することでルール3になっている
今までルール1,2,3の3つのルールを考える必要がありましたが、四角い石（□・■）の外側に石を追加することはないので、ルール3を考えるだけで良くなりました。非常に嬉しいです。
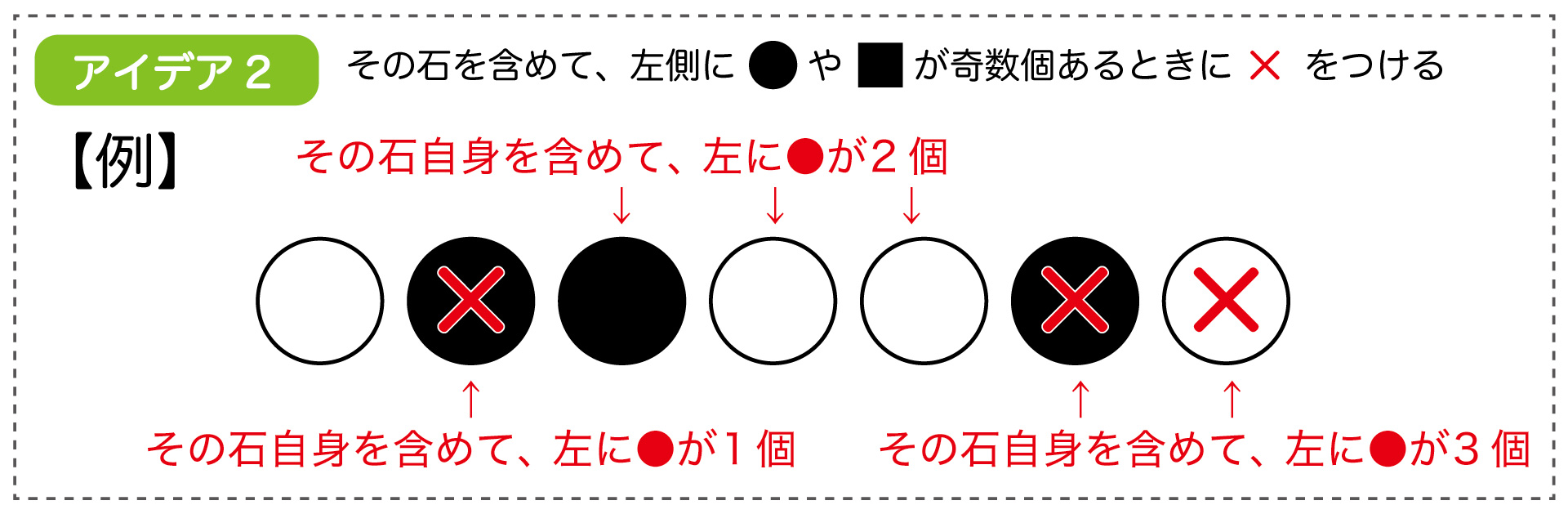
【アイデア2】並んでいる石の上に、ルールに従って×印が表示されるようにする
「その石より左にある石（その石自身を含む）の中に、黒石（●・■）が奇数個あれば×を表示する」というルールを使います。
「なぜ急に×をつけるの？」と疑問に思う方もいるかもしれませんが、×を使うことで証明がうまくいくんです！ 詳しくはこれからご説明します。
×の増え方の規則性を見つけよう！
○を追加していく様子を、アイデア1,2を用いて観察してみると、以下のようになります。
×の数の変化に注目してみると、〇を1個追加することで全体の×の数は「2増える」または「1減る」のどちらかだと予想できます。
これがすべての場合でも成り立つことを確かめるために、〇を1個追加するときの×の変化を以下の図のように3つのブロックに分けて見ていきます。
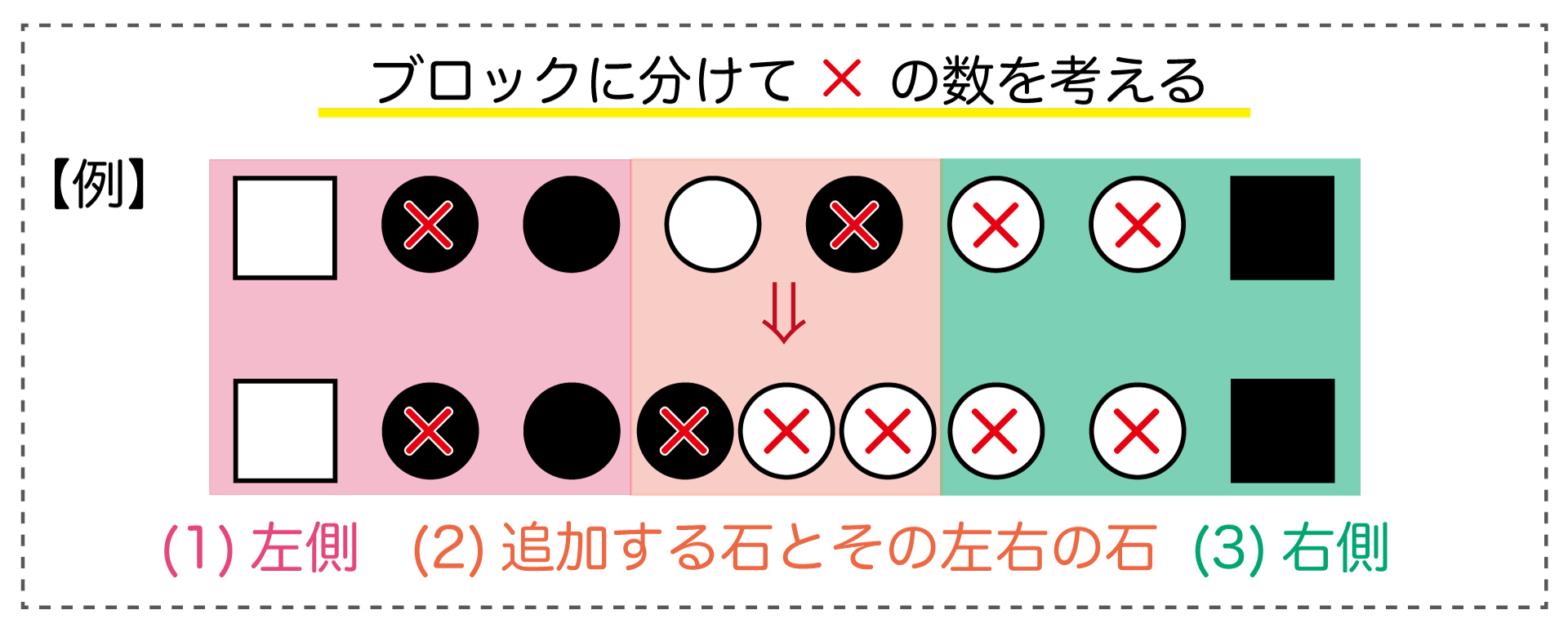▲「追加する石とその左右の石」の3個を中心に、3つのブロックに分ける
まず、(1)左側のブロックについて考えます。×の数はその石を含めて左にある●や■の数に変化があったときに変わるため、〇を追加しても(1)左側の×の位置に影響はありません。
次に(2)追加する石とその左右の石についてです。追加前の〇、●、×の組み合わせを考えると、以下の8種類しかないことがわかります。
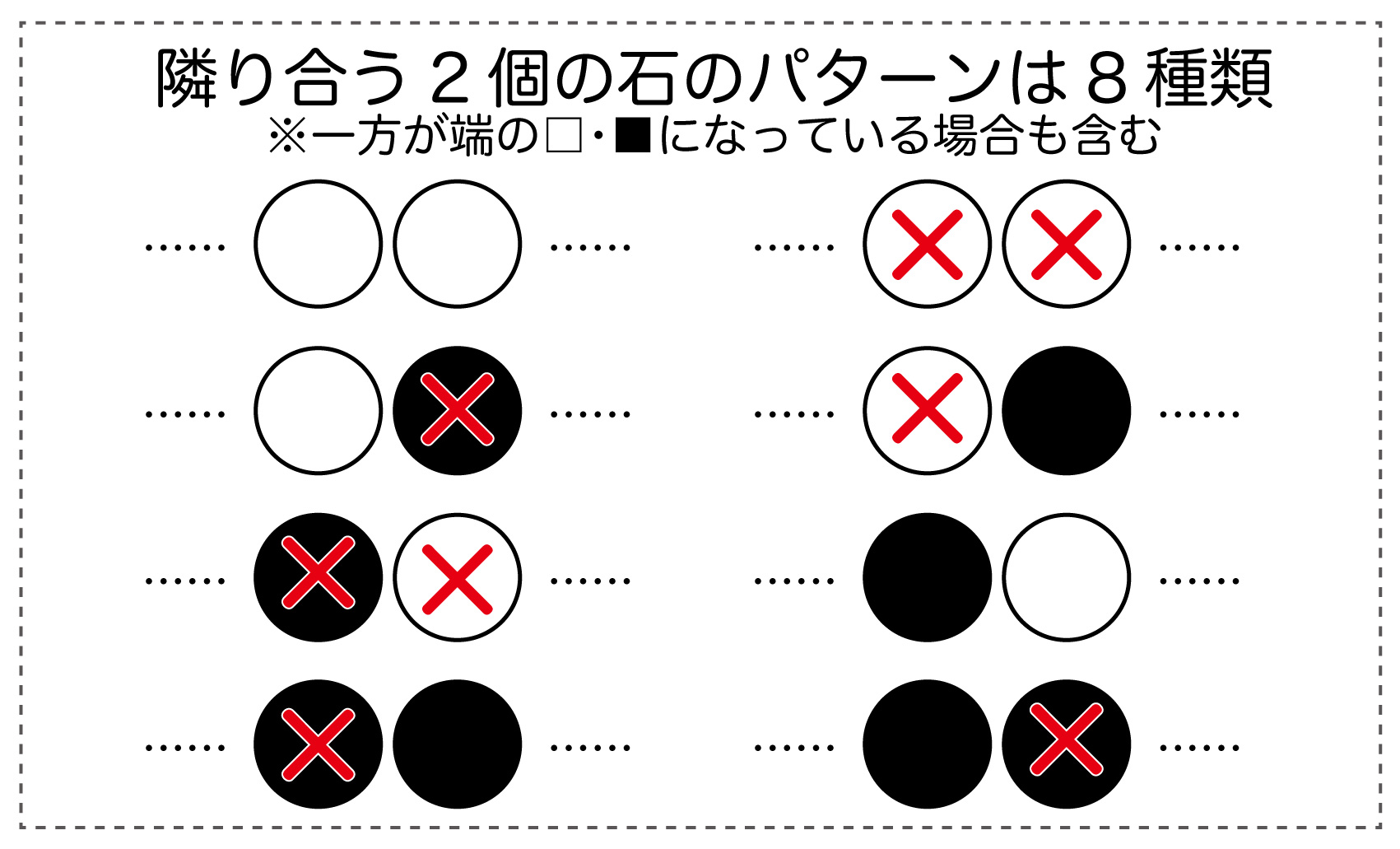▲例えば、〇〇の左に●,■が偶数個ある場合は×は2つともつかず、奇数個ある場合は×は2つともつく
また、〇を追加したときの×の増え方/減り方のパターンは、すべての場合において「2増える」または「1減る」のどちらかであることが確かめられます。
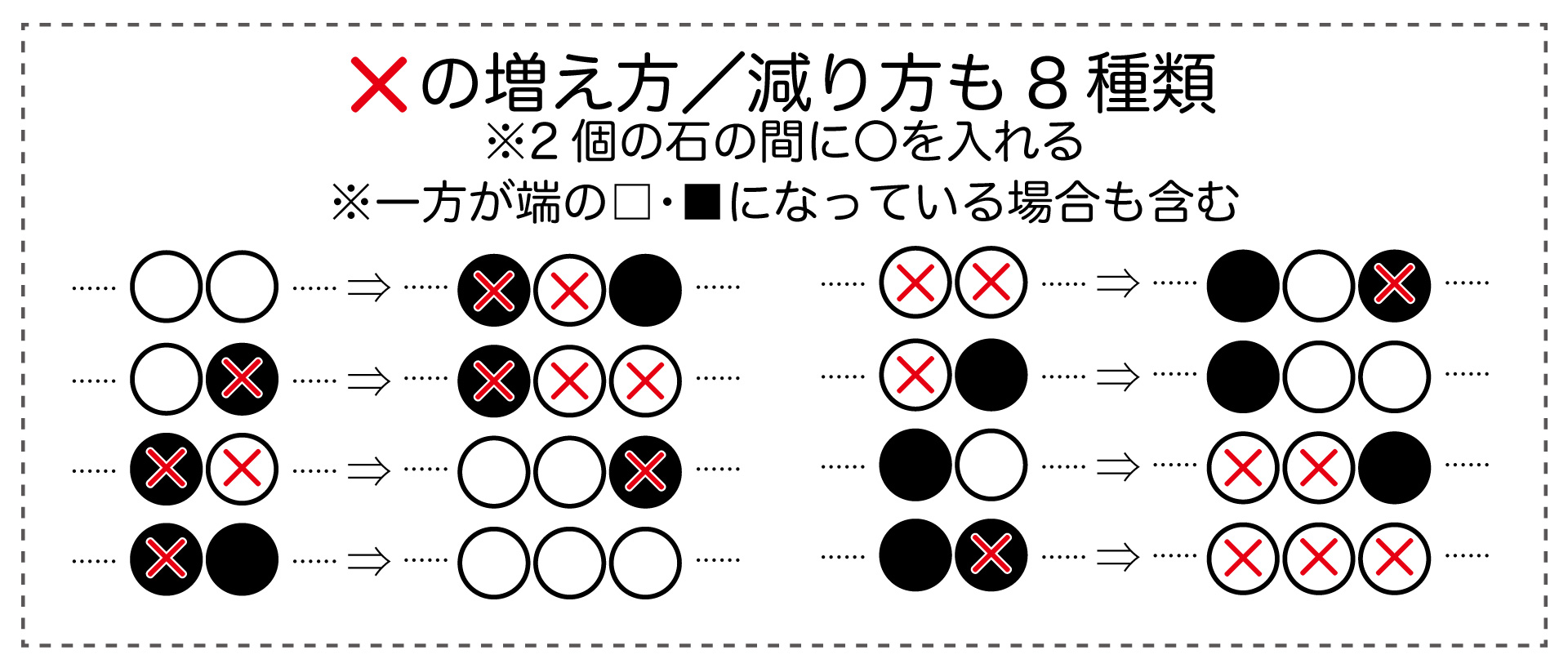▲×は「2増える」「1減る」のいずれかになっている
また、下の図からもわかるように、(3)右側のブロックの×の位置や個数も変わりません。
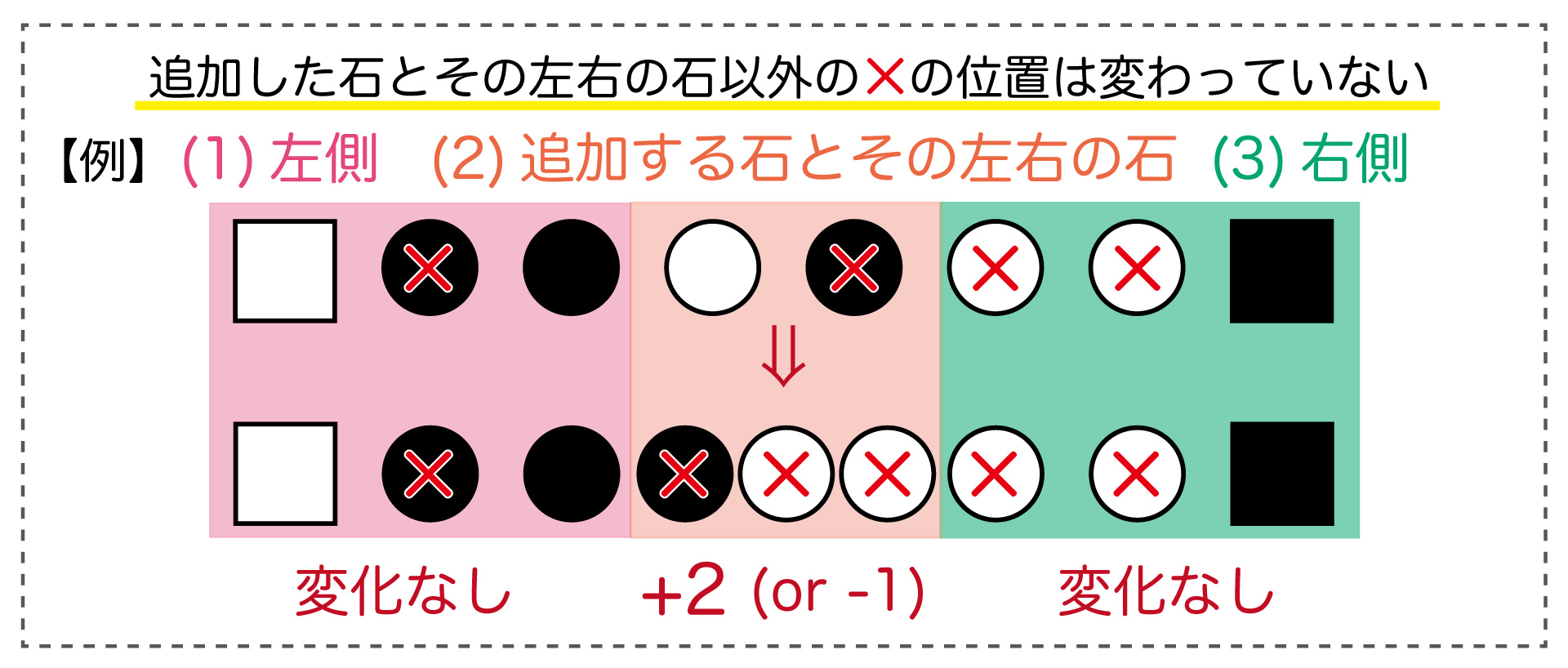
※(3)右側のブロックの×の位置が変わらないことを厳密に証明するなら、(1)と(2)の黒石（●・■）の数の偶奇が、〇の追加前後で変わらないことを示せば良いです。
これらのことから、〇を1個追加したとき、すべての場合で全体の×の数は「2増える」または「1減る」のいずれかになるということがわかりました。
×を使って「隠れた規則」を見つけることができました！ 嬉しい！
さて、〇をn-1個追加するとき、×の数について「2増える」がk回あるとすれば、「1減る」はn-1-k回あります。最初にある×の数は0個なので、n-1(=3m+1)個追加した後の×の数は、3(k-m-1)+2 個となります。
つまり、どんな方法で〇をn-1(=3m+1)個追加しても、×の数を3で割ると余りは2になります。
アイデアを駆使して、×の数の矛盾を導こう！
先ほどは「どんな方法で〇をn-1個追加しても、×の数を3で割った余りは2になる」ことを証明しました。つまり「もし〇がn個並んだとき、×の数を3で割った余りは2にならない」ことを証明できれば、〇がn個並ばないことが証明できます。
〇がn個並んでいるとき、両端の石の色の組み合わせは□□、□■、■□、■■のいずれかになります。
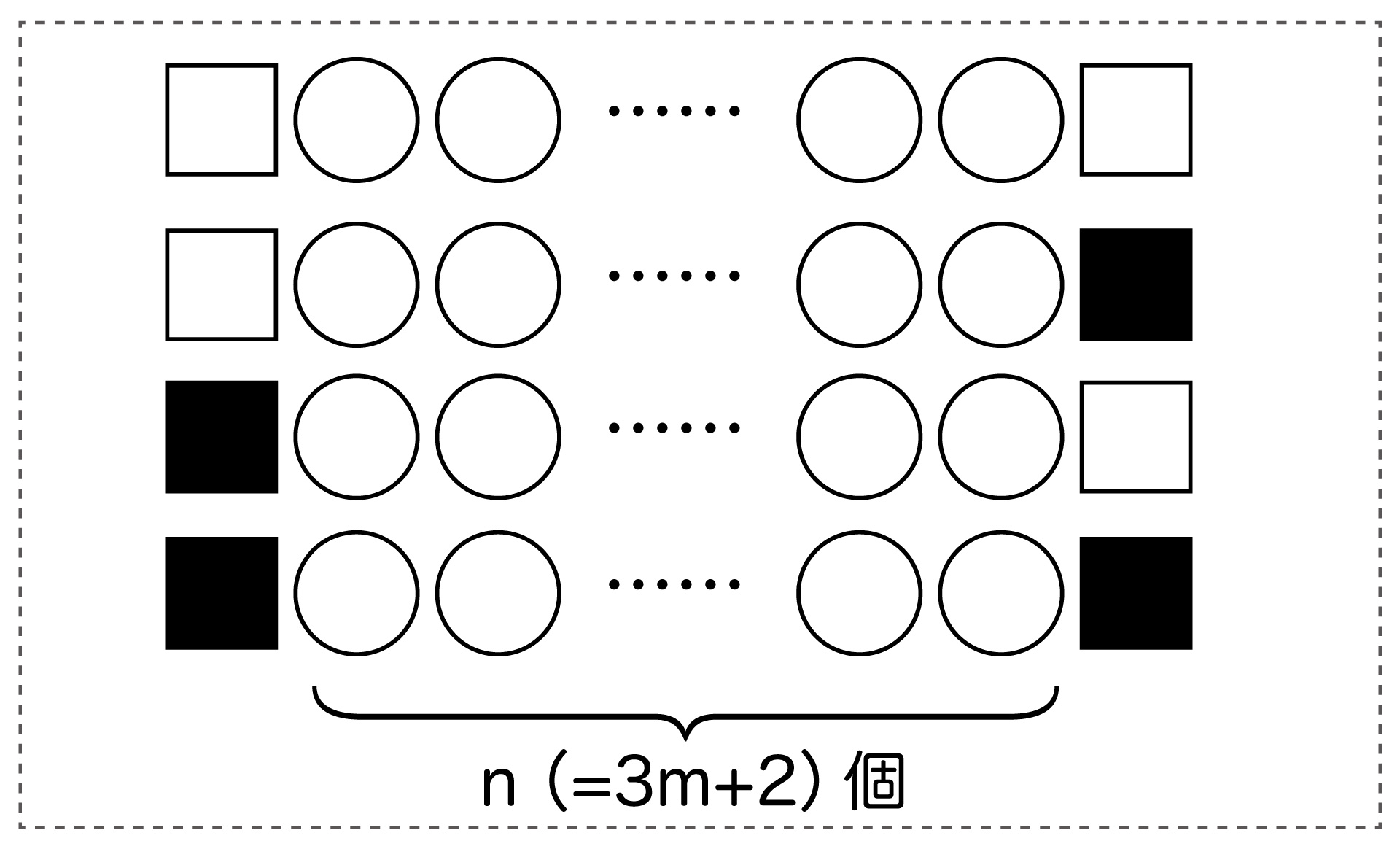
これに×をつけると、以下のようになります。
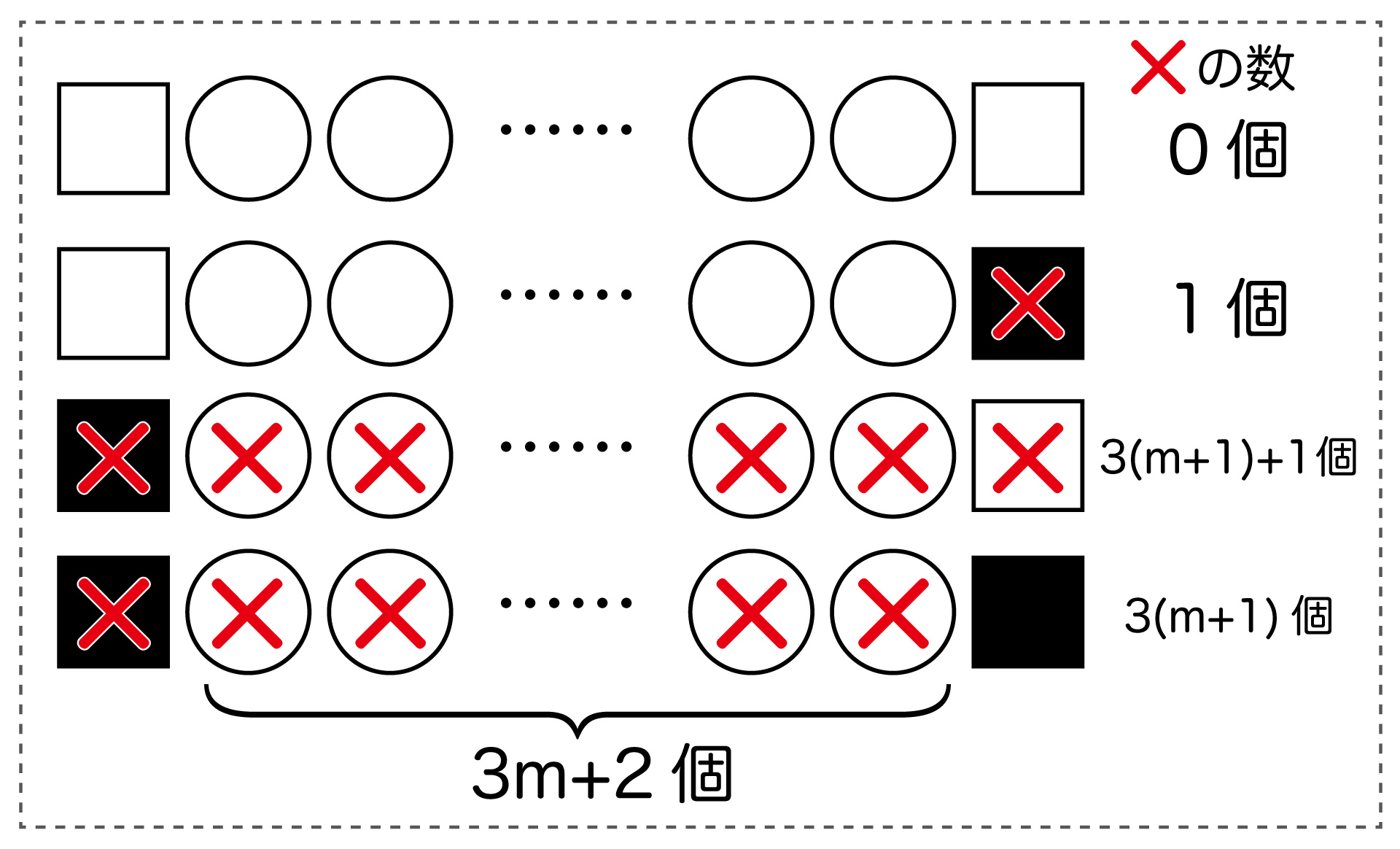▲×の数を3で割った余りは、0か1になっている！
つまり、もし〇をn個並べることができれば、×の数を3で割った余りは0か1になります。しかし先ほど「どんな方法で◯をn-1個追加しても、×の数を3で割ると余りは2になる」ことを証明したため、矛盾します。
したがって、〇をn=3m+2個並べることは不可能です。前半の証明と合わせると、「n個の石をすべて〇にすることができる」という条件を満たすnは「3で割った余りが0か1になるようなn」であることがわかります。（証明終わり）
これで証明は終わりです。お疲れ様でした！
おわりに
無事証明ができたということで、ここまでの流れをおさらいしてみましょう。
上記のステップで、nの条件を求めました。
1ステップずつ解決していくことで、最初の問題文を見たときに感じた「難しそう」という印象が、少し変わったのではないでしょうか。
この問題のポイントは以下の3つです。他の数学の問題を解くときにも、このポイントを意識してみると良いかもしれません。
なお、今回紹介した解答はあくまで一例です。一般的によく知られている解答では、二面体群D3を用いて証明しています。非常にエレガントな証明で、群について知らなくても行列の積の計算を知っていれば理解できるので、興味のある方はぜひ参考文献をご参照ください。
参考文献
【あわせて読みたい】
