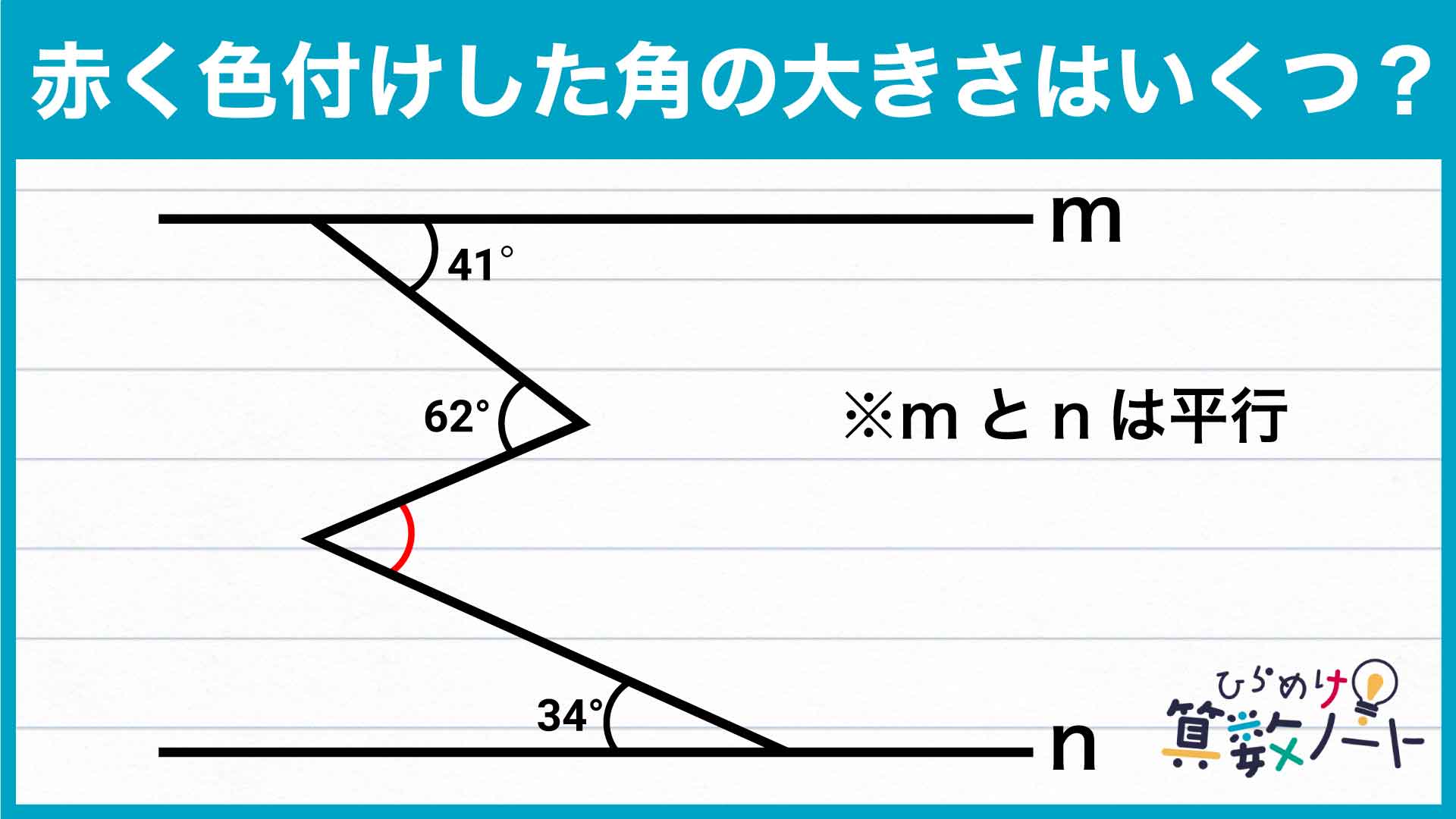
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
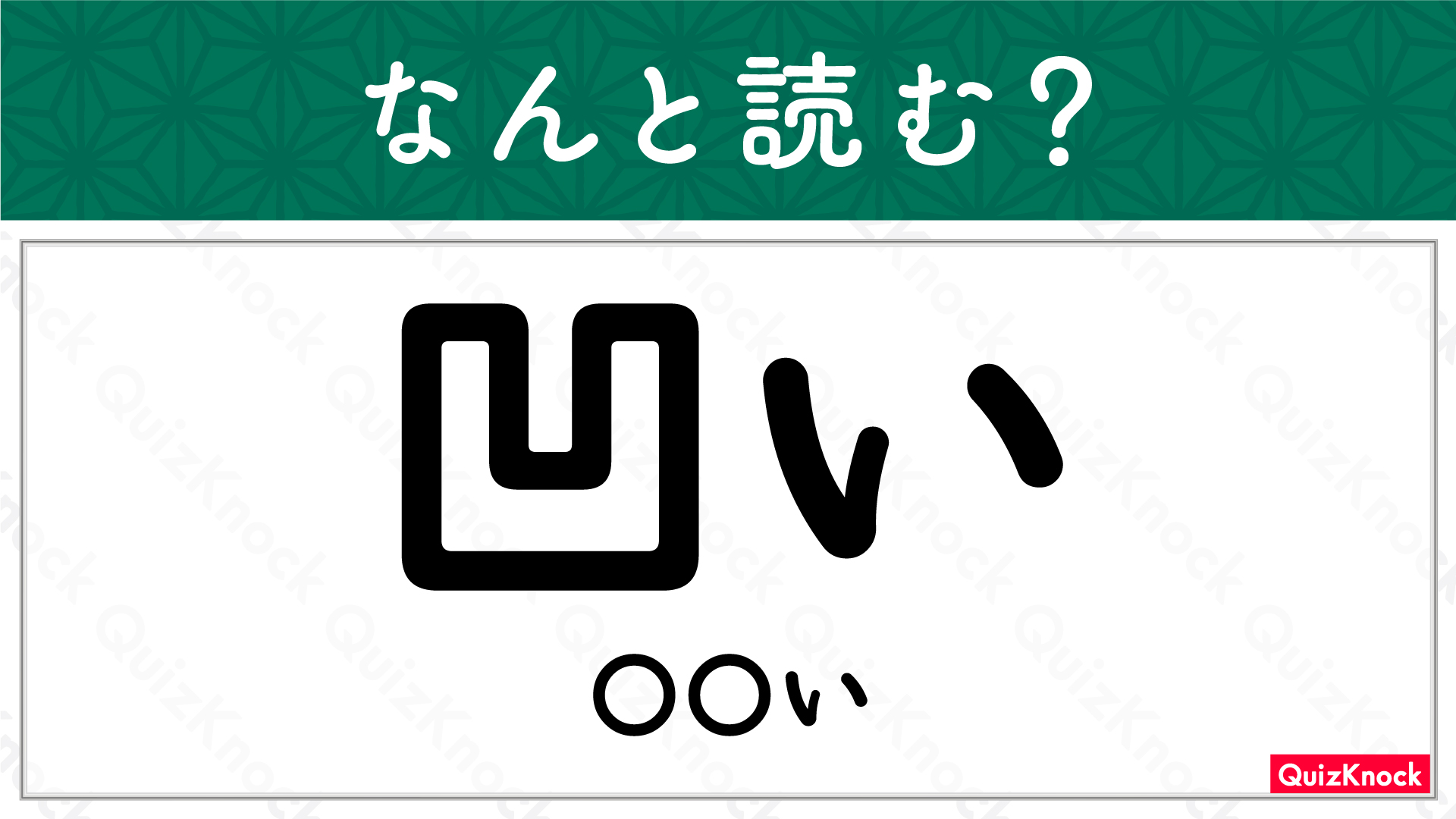
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです。
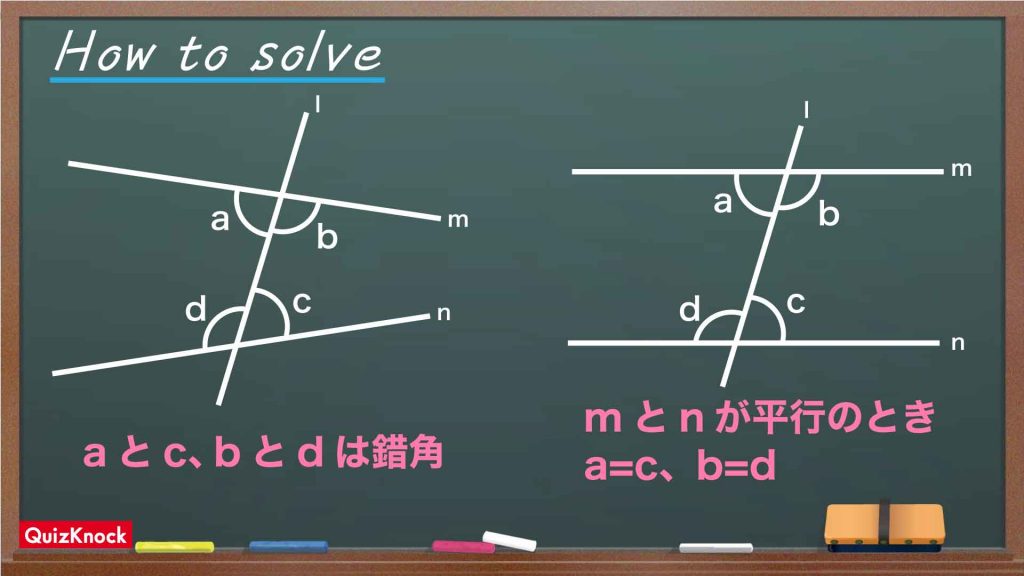
今回のポイントは「錯角」です。下の図のように、同一平面上の直線 l が2本の直線(mとn)と交わるとき、直線mと直線nの内側にあり直線 l の反対側に位置する2つの角の組を錯角といいます。直線mと直線nが平行のとき、錯角の大きさは互いに等しくなる性質があります。
この性質を踏まえ、順に解いていきましょう!
補助線を引く
まずは、補助線を引いていきます。
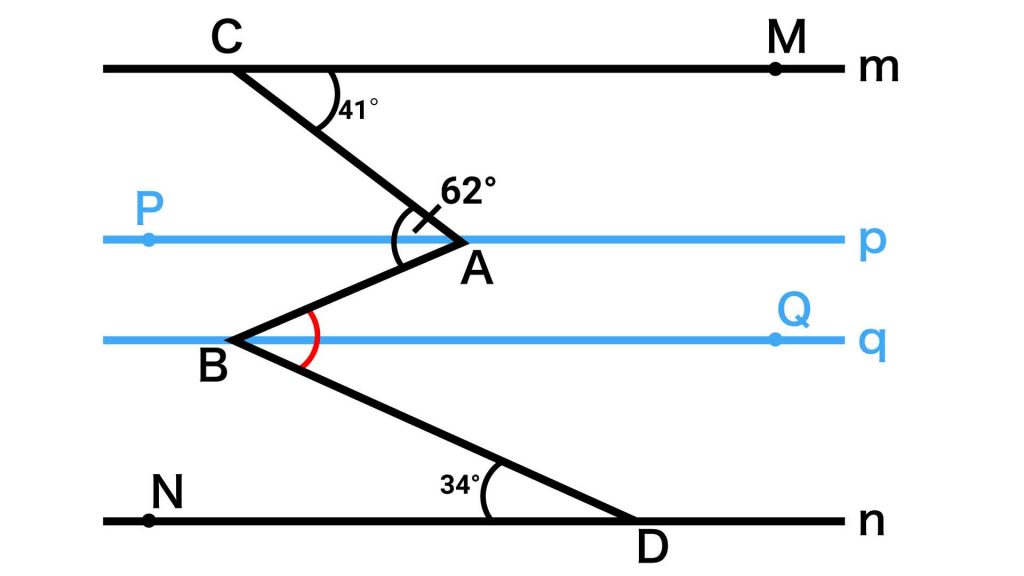
下の図のように、点A、Bをそれぞれ通り、上下2本の直線に平行な2本の直線p、qを引きます。
また、解説しやすくするため、下の図のように点C、D、M、N、P、Qを定めます。
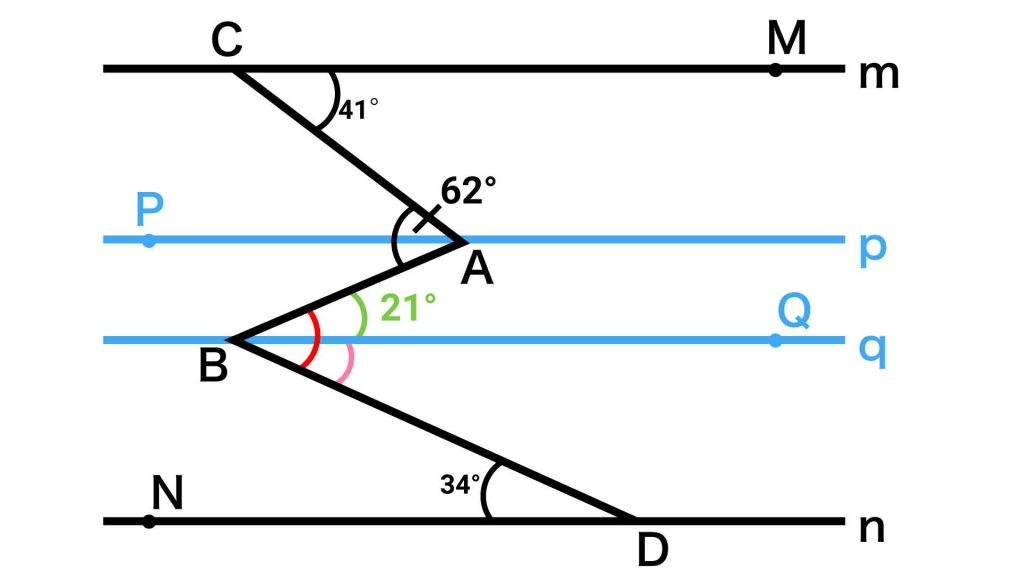
補助線qを引いたことで、赤い印を付けた角は、角ABQと角QBDという2つの角に分かれました。ここからは、錯角を使ってそれぞれの角度を調べていきます。
同じ角度を持つ角の組み合わせを見つける
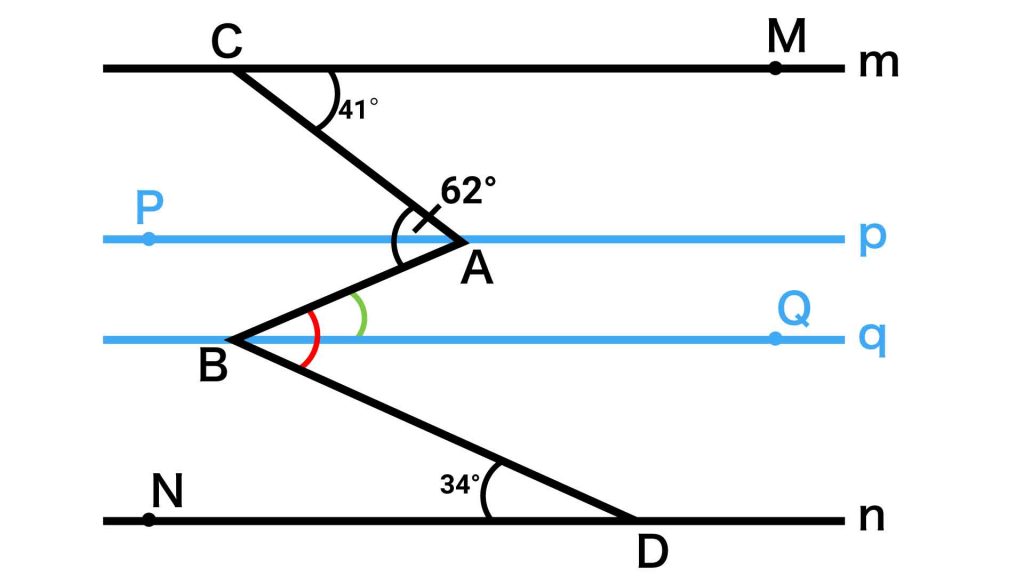
まずは、下の図で緑色で示した角ABQについてです。
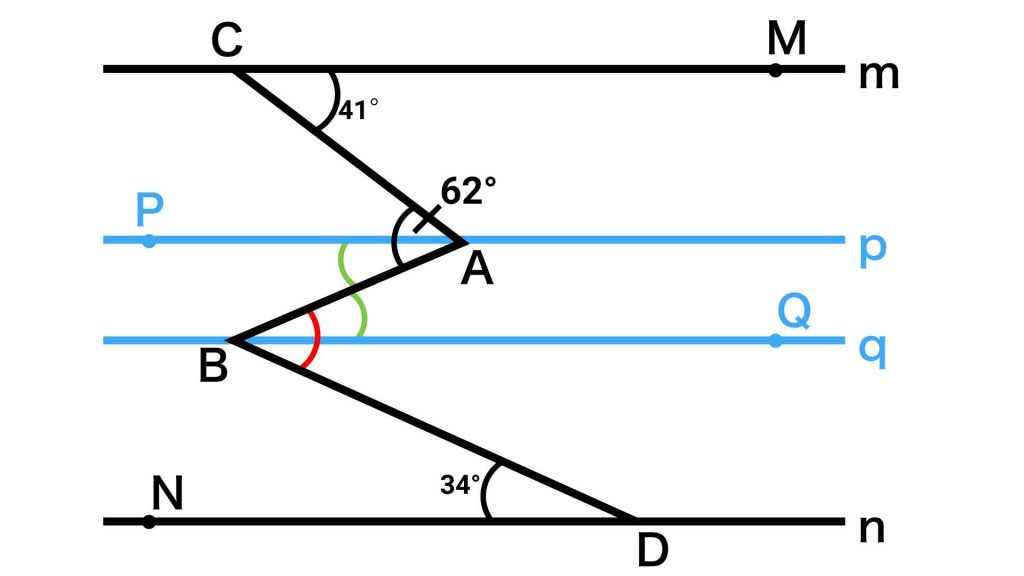
直線pとqは平行なので、錯角の関係にある角ABQと角PABの大きさは等しくなります。
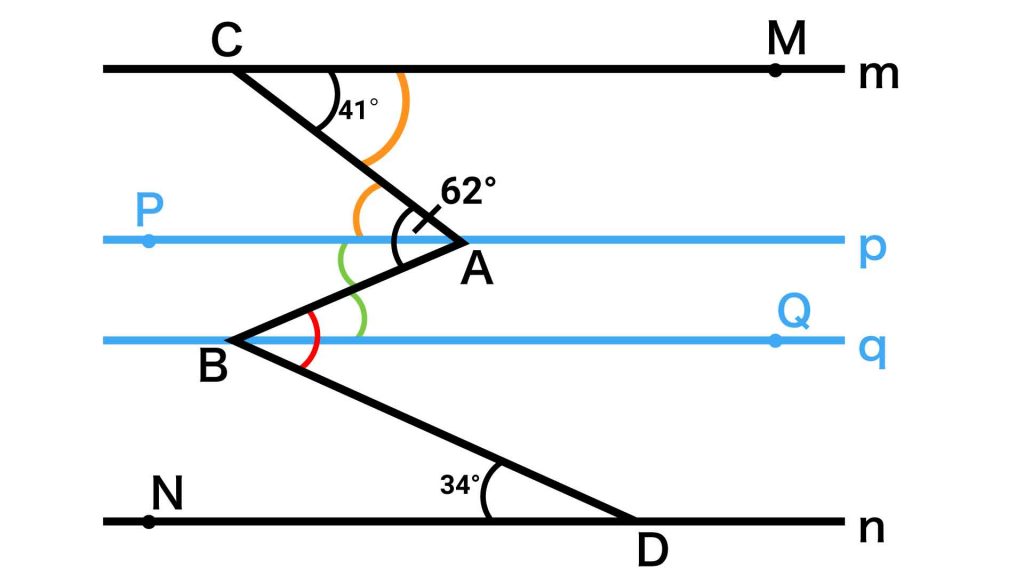
一方、直線mとpは平行なので、錯角の関係にある角MCAと角CAP(以下の図ではオレンジ色で表記)の大きさは等しくなります。
したがって、緑とオレンジの角の大きさを合計すると62度になることがわかります。オレンジの角の大きさは41度なので、緑の角(角ABQ)の大きさは62-41=21度となります。
次に、下の図においてピンク色で示した角QBDについてです。
直線qとnは平行なので、錯角の関係にある角QBDと角BDNの大きさは等しくなります。角BDNの大きさは34度なので、角QBDの大きさも34度となります。
最後の総仕上げ
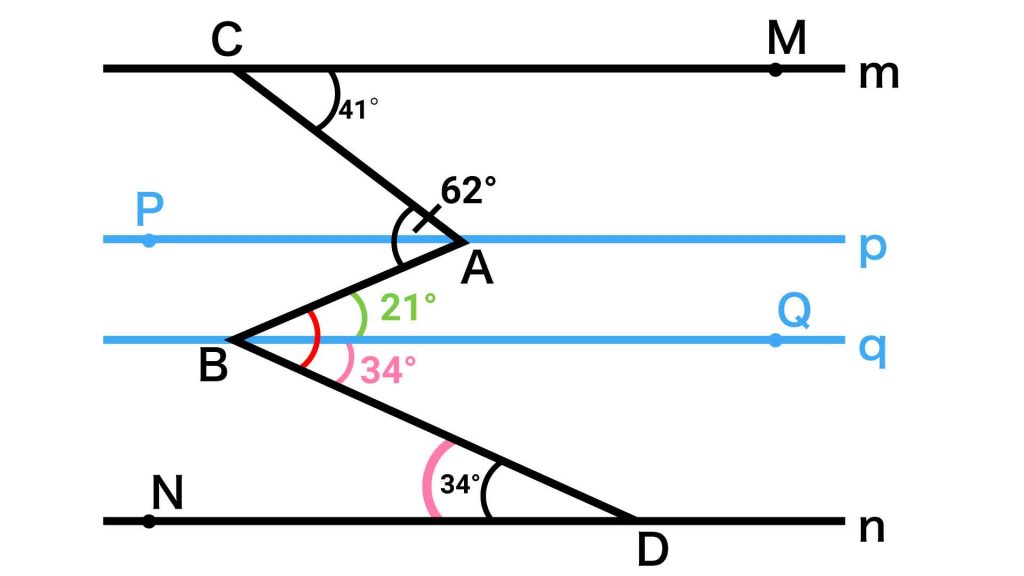
赤い角は、角ABQと角QBDから構成されています。
角ABQの大きさは21度、角QBDの大きさは34度なので、赤い角の大きさは21+34=55度となります。
答え:55度
それでは、次回の算数ノートでお会いしましょう。
「ひらめけ!算数ノート」のバックナンバーはこちらからどうぞ。
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)







.jpg)