解説
それでは解説です。この問題についてはさまざまな解き方がありますが、ここでは「小学5年生で解ける」解き方を紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです。
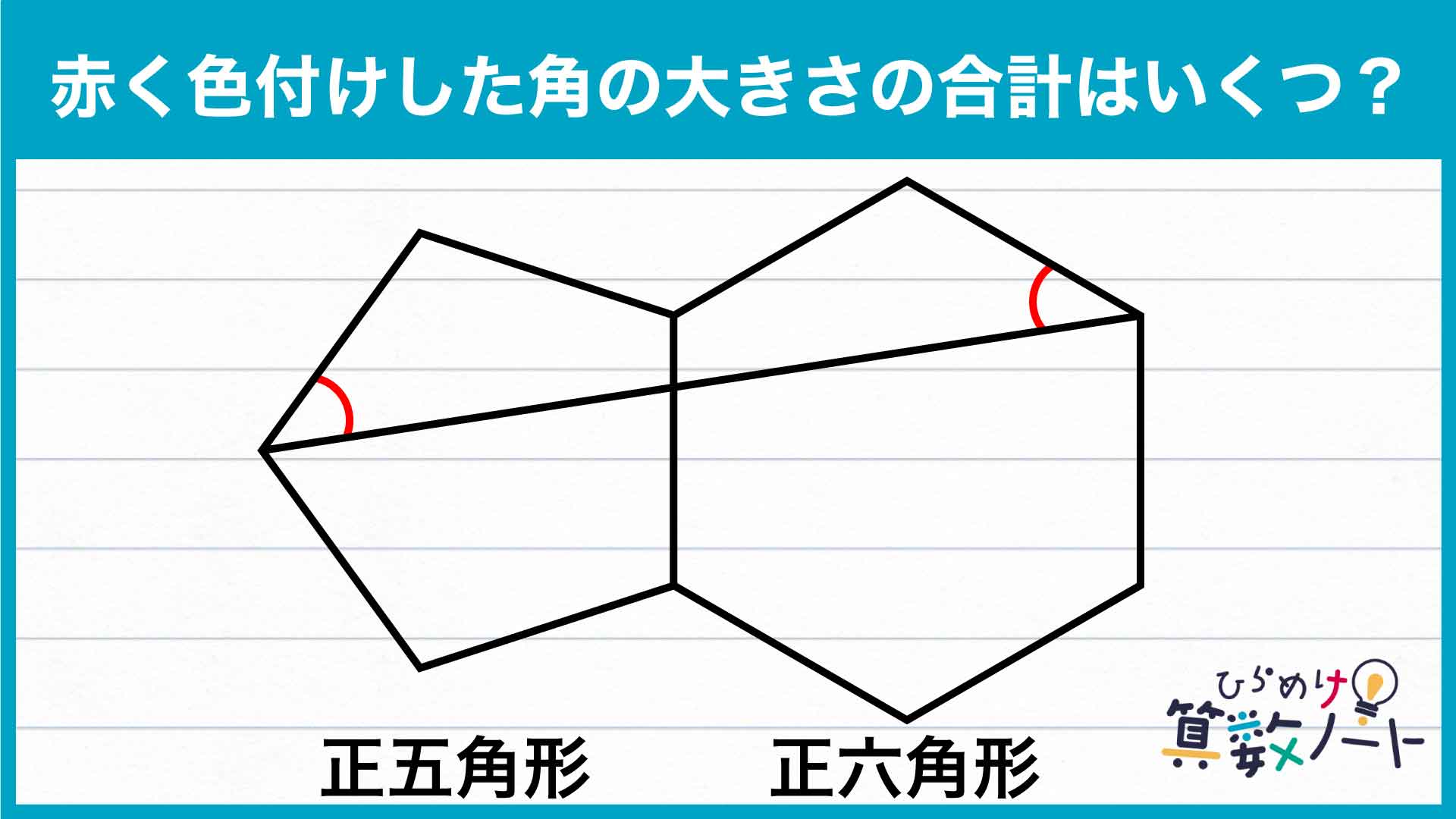
今回の問題を解く上で重要なポイントをまとめた図がこちらです。
「ひらめき力」を最も要するのが、補助線を2本引く部分でしょう。
ここを乗り越えることができれば、一気に答えに近づくことができます。
補助線を2本引く
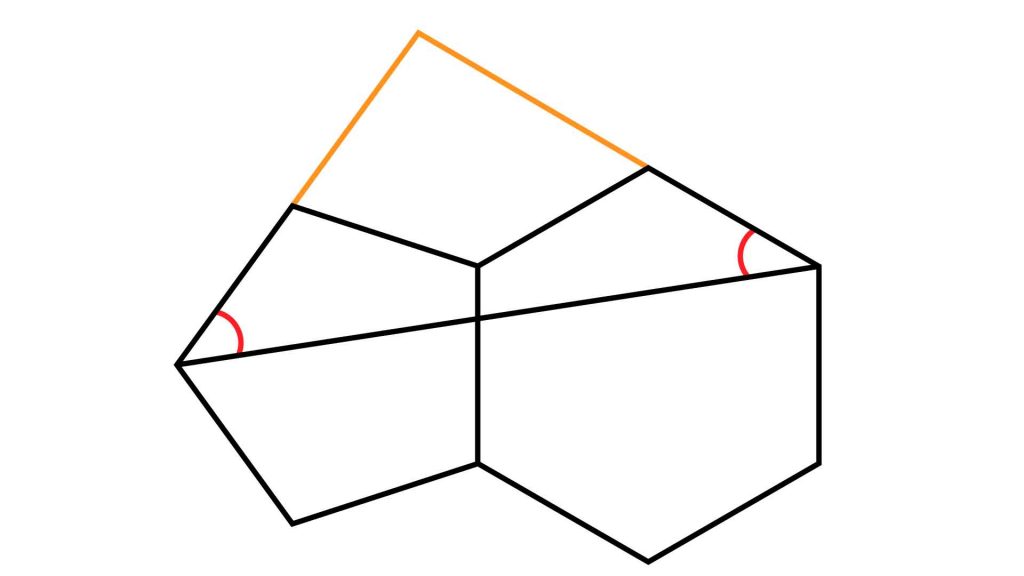
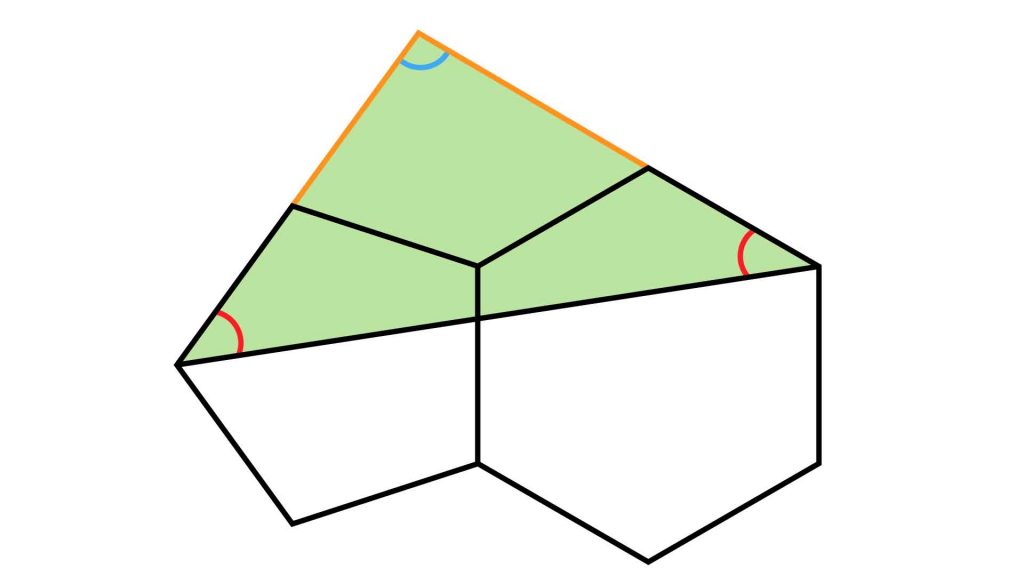
まずは、補助線を引きます。今回引く補助線は、下の図のオレンジの線で表されている2本です。
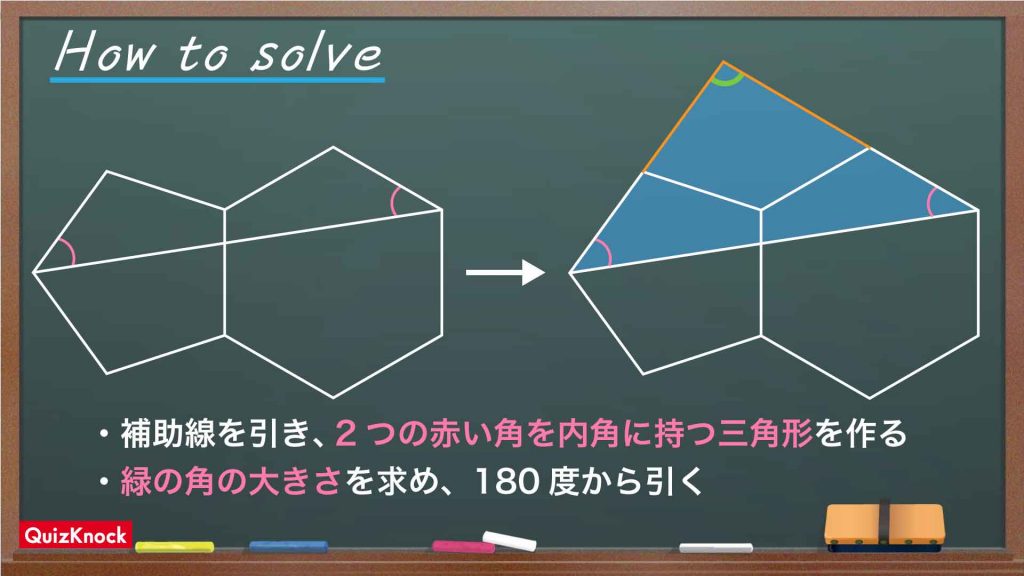
この補助線を引くことで、2つの赤い角を内角に持つ三角形ができます。
最終的に求めるのは2つの赤い角の大きさの合計なので、下の図の、緑の三角形の内角の合計である180度から、青い角の大きさを引けば、答えを出すことができます。
青い角の大きさを求めるには……?
ここからは、青い角の大きさを求めていきます。
青い角の大きさを求めるにあたって必要な情報が、正五角形と正六角形の内角の大きさです。
正五角形と正六角形について、1つの内角の大きさは以下の通りです。
- 正五角形:108度
- 正六角形:120度
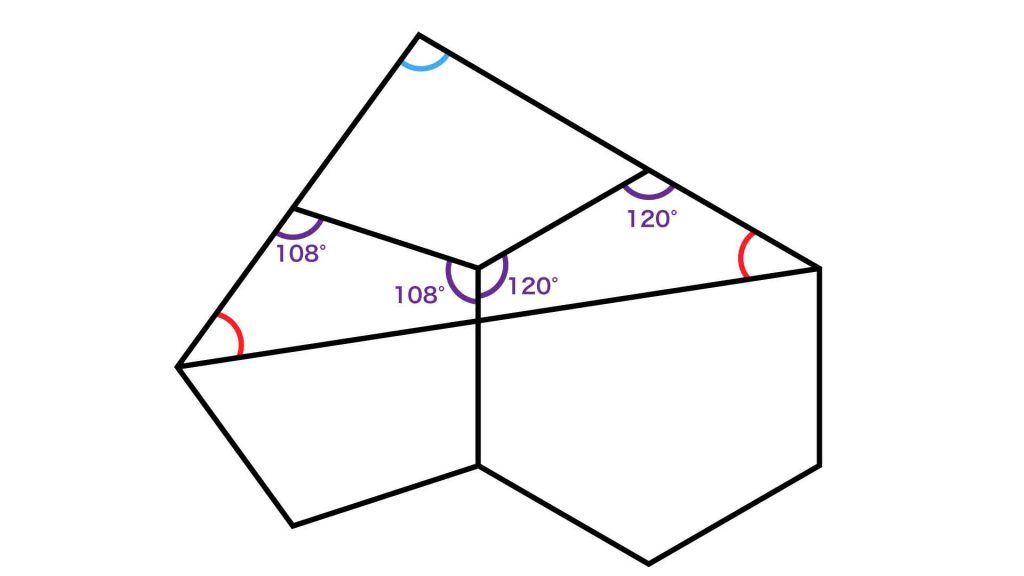
これらに基づき、青い角の大きさを求めるのに必要な内角の大きさを書くと、下の図のようになります。
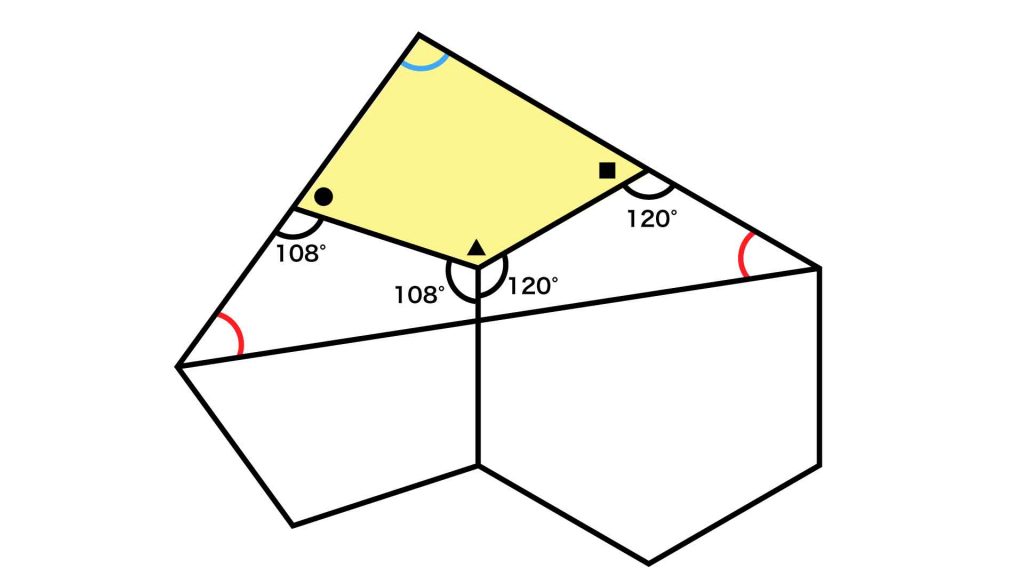
ここで、下の図の黄色い四角形と、●、▲、■という3つの角に着目します。
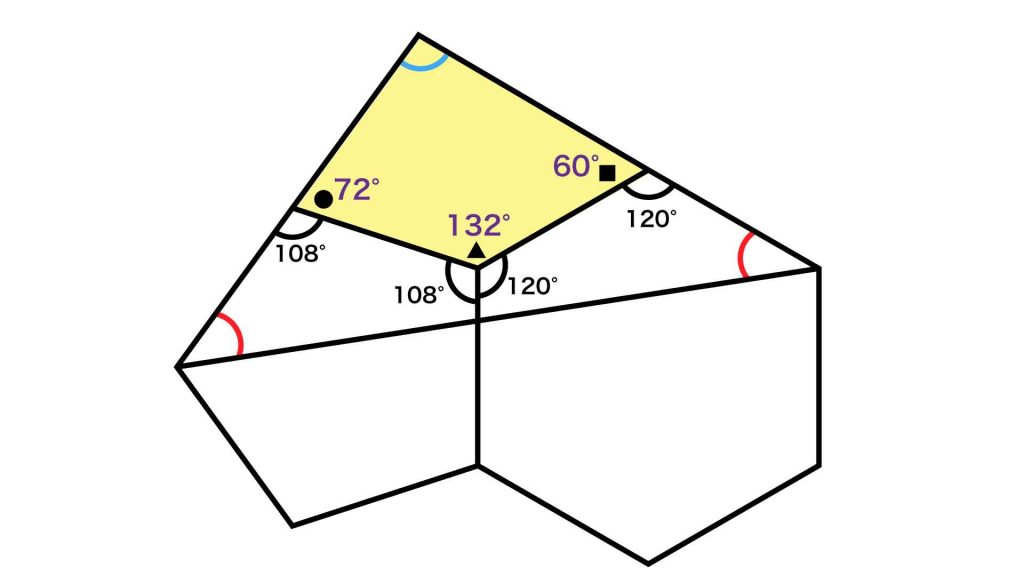
●の角について、●の角の大きさと108度の合計が180度になるので、●の角の大きさは、180-108=72度です。
同様に、■の角について、■の角の大きさと120度の合計が180度になるので、■の角の大きさは、180-120=60度です。
また、▲の角について、▲の角の大きさ、108度、120度の合計が360度になるので、▲の角の大きさは、360-(120+108)=132度です。
以上より、黄色い四角形の3つの内角の大きさは、以下のようになります。
黄色い四角形の内角の和は360度なので、青い角の大きさは、360-(72+132+60)=96度となります。
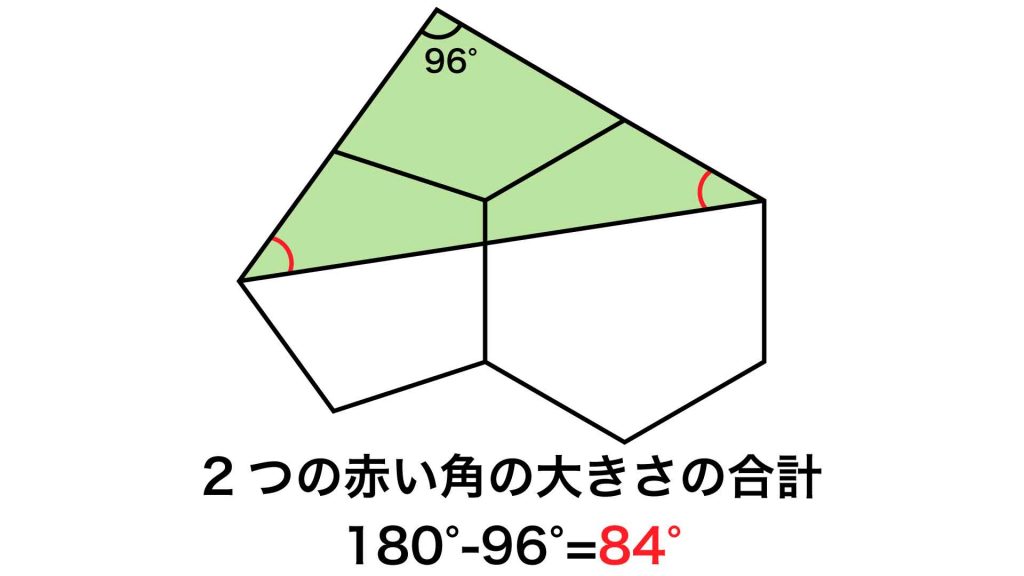
2つの赤い角の大きさの合計を求める
青い角の大きさが求められたので、再び緑の三角形に着目します。
緑の三角形の内角の合計は180度、青い角の大きさは96度なので、2つの赤い角の大きさの合計は、180-96=84度となります。
答え:84度
それでは。
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)







.jpg)







