解説
それでは解説です。
前ページ：【解答フォーム】自力で解きたい方はこちらへ！ 以下は問題の答えです。
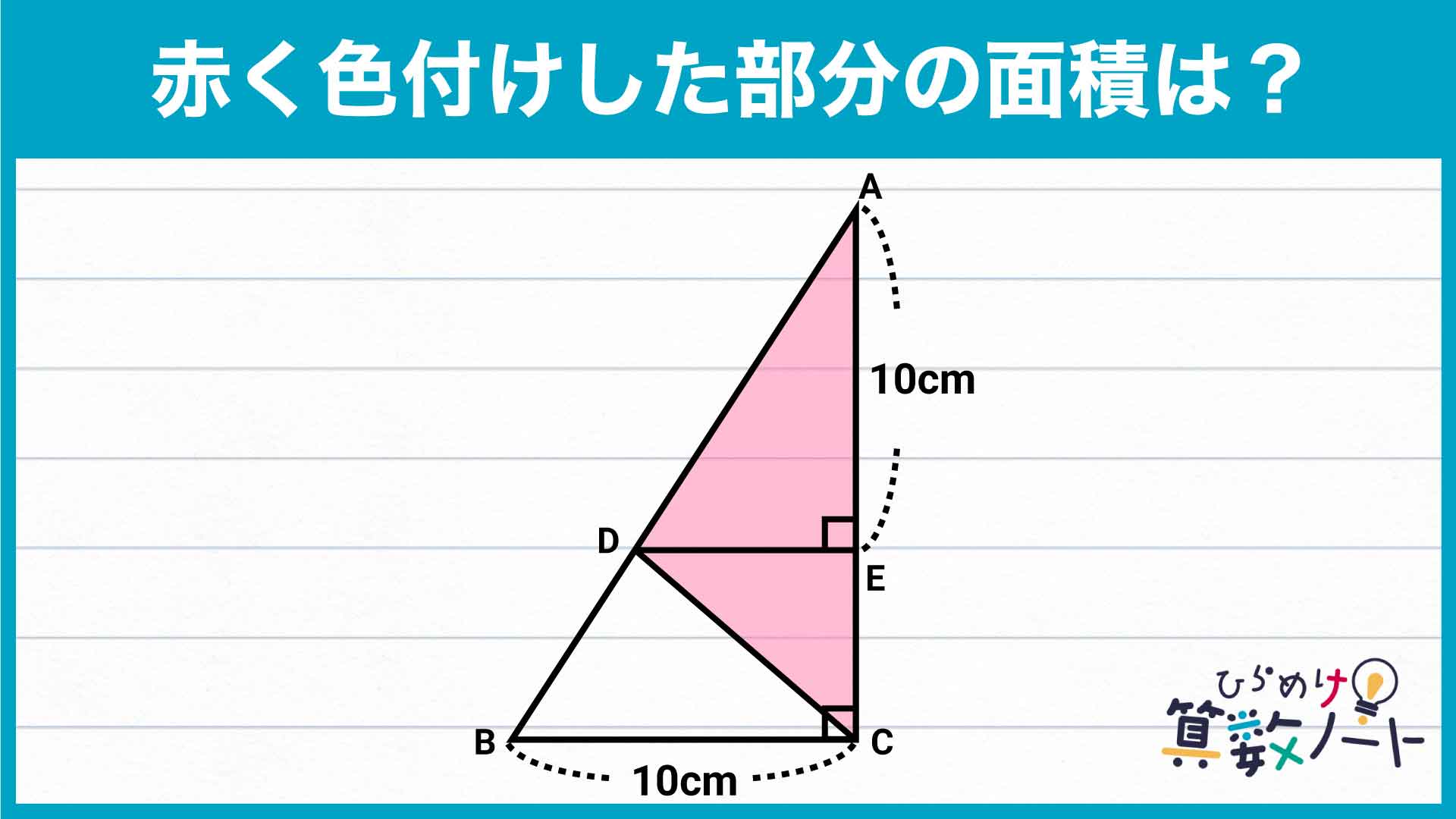
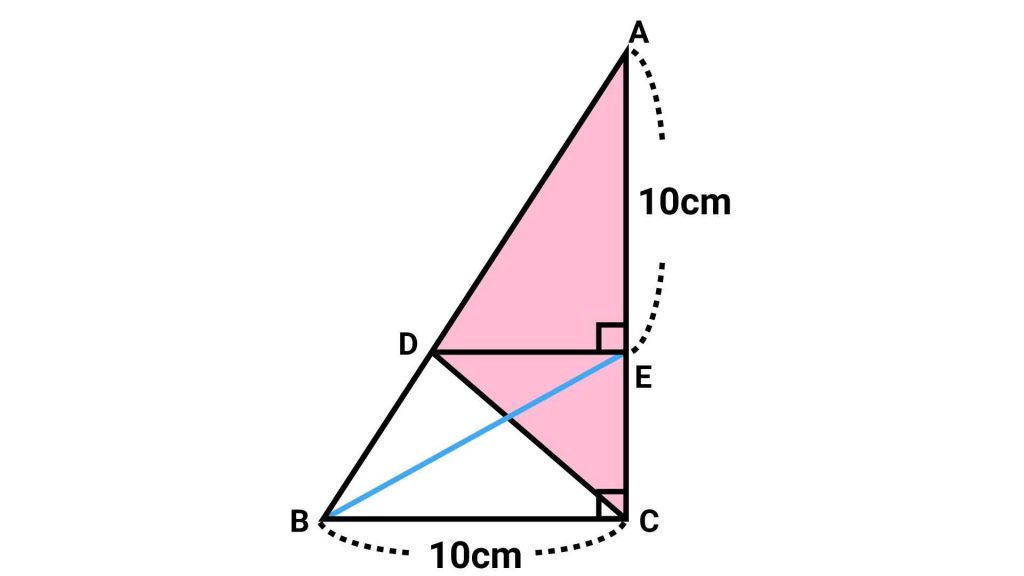
今回は私と一緒に解いていきましょう！ 面積を求めたい三角形ADCの各辺の長さがわかっていませんが、どのように解いていくのでしょうか？
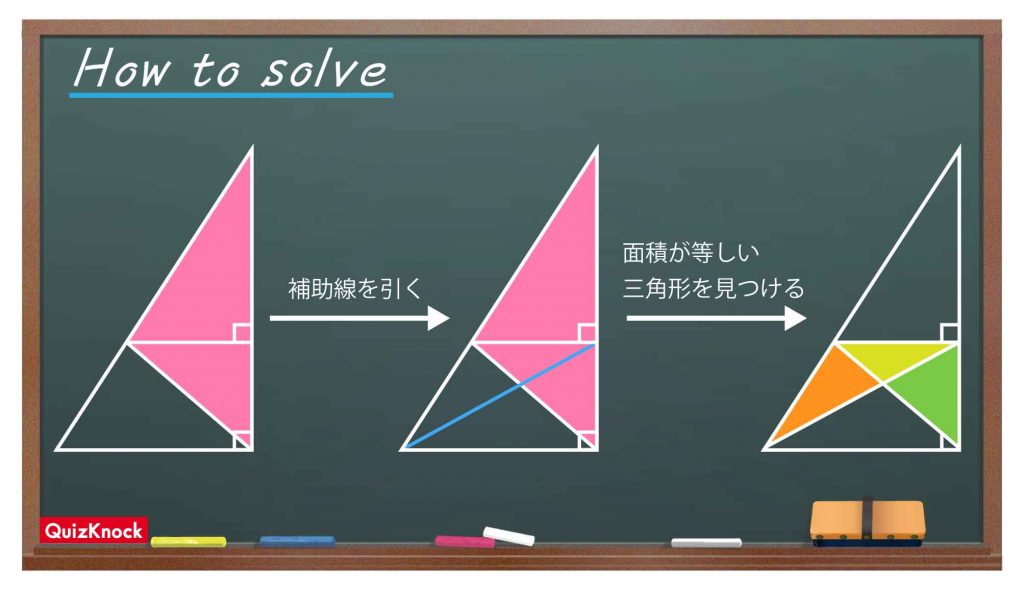
今回の問題の解き方をまとめた図がこちらです。ポイントは補助線を引き、面積が等しい三角形を見つけることです。
この図の流れに沿って、順に解いていきましょう！
補助線を引く
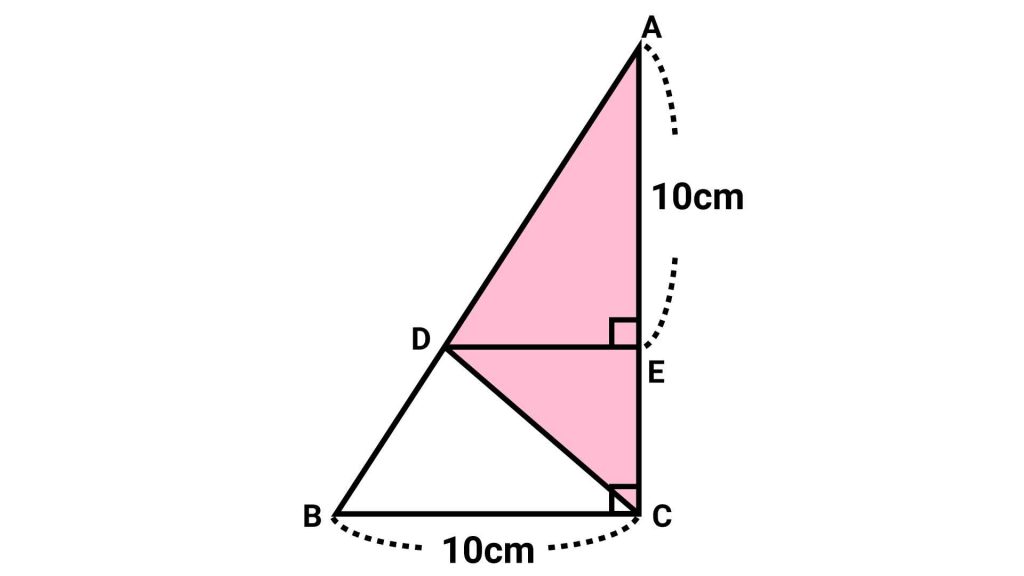
まず、以下の図のように点Bと点Eを結ぶ補助線を引きます。
この補助線が、問題を解く上で最大のポイントです。
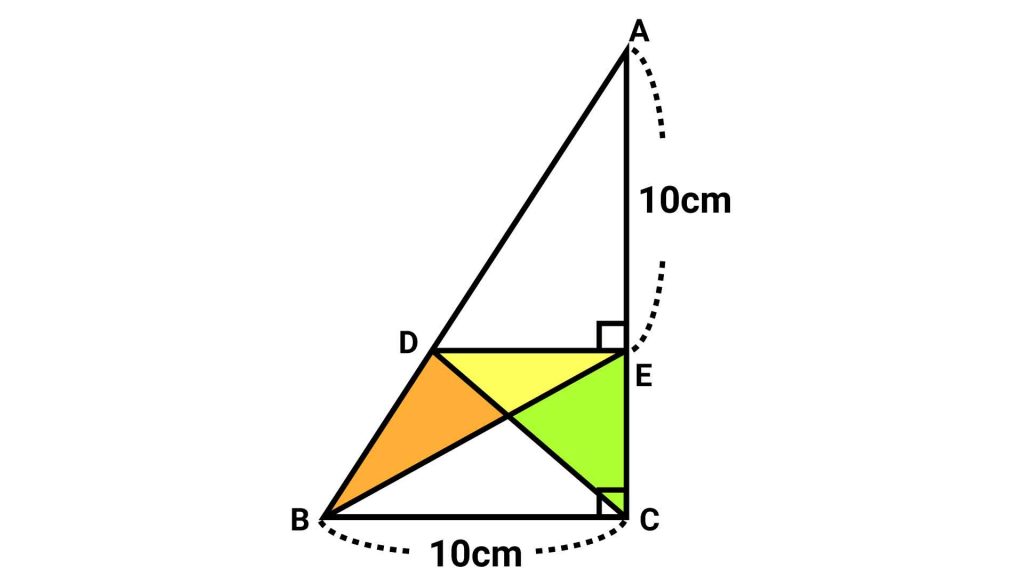
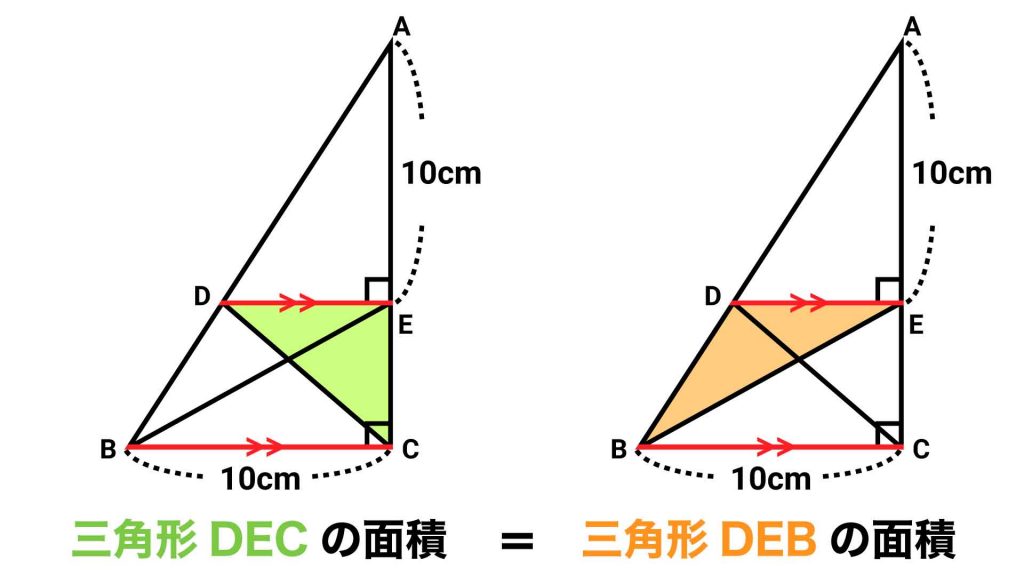
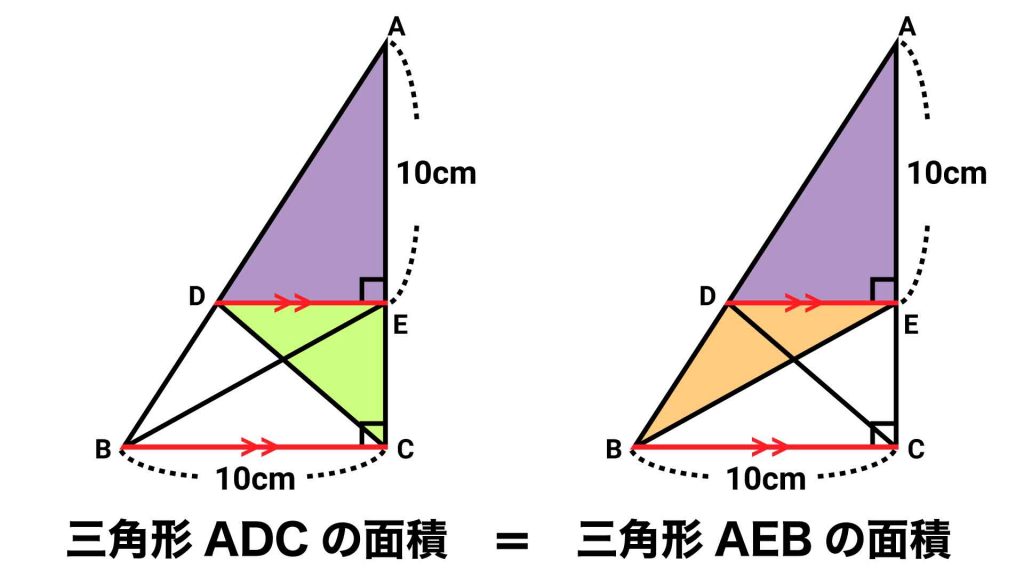
三角形DECと三角形DEBに注目する
次に、三角形DECと、補助線を引くことによってできた三角形DEBに着目します。
角ACBと角AEDが直角であることから、直線DEと直線BCが平行になることをふまえると、三角形DECと三角形DEBには、以下の共通点があります。
- 辺DEを底辺として共有している
- 辺ECを高さとして共有している
したがって、三角形DECと三角形DEBの面積は等しくなります。
こうすることで、面積を求められるようになるのです！
三角形ADCと面積が等しい三角形は？
ここで、面積を求める三角形ADCに着目します。
この三角形は、三角形ADEと三角形DECを組み合わせた図形です。
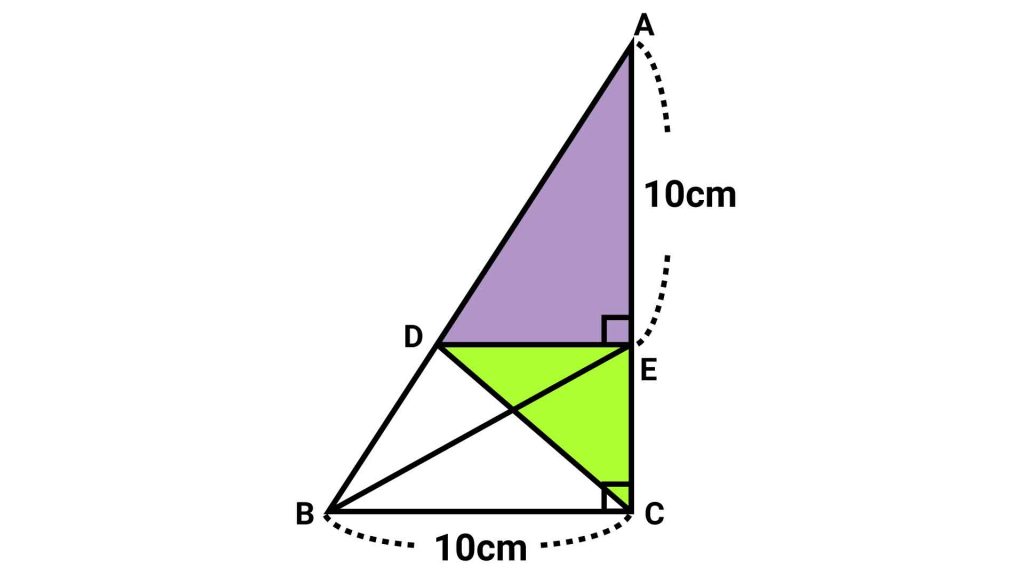
このうち、三角形DECは三角形DEBと面積が等しいことがわかっています。
したがって、三角形ADCは、三角形ADEと三角形DEBを組み合わせた図形、すなわち三角形AEBと面積が等しくなります。
三角形AEBは、底辺である辺AEの長さが10cm、高さである辺BCの長さが10cmであることから、面積は10×10÷2=50cm2となります。
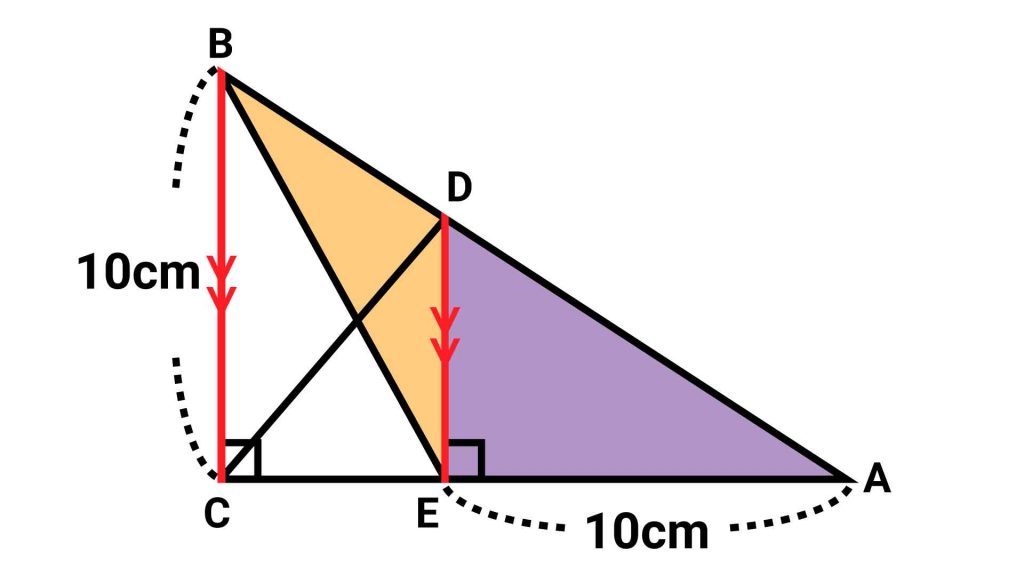▲90度右に回転させると、底辺と高さにあたる辺がよくわかる！
求めたい三角形ADCの面積は三角形AEBの面積と等しいので、50cm2です。
答え：50cm2
補助線を引き、面積が等しい三角形を見つけることがポイントでした。
「ひらめけ！算数ノート」のバックナンバーはこちら！
【前回の算数ノートはこちら】
【あわせて読みたい】
