解説
それでは解説です。この問題についてはさまざまな解き方がありますが、ここでは「小学5年生で解ける」解き方を紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです。
今回は僕と一緒に解いていきましょう! 一見、簡単に答えを出せそうな気がしますが……。
今回の問題で重要なポイントは、次の2点です。
- 合同な三角形に着目すること
- 角度が等しい角を見つけ出すこと
この2つのポイントを使う前に、問題を解くのに必要な情報を整理しておきましょう。
まずは、答えを出すのに何の情報が必要かを調べる
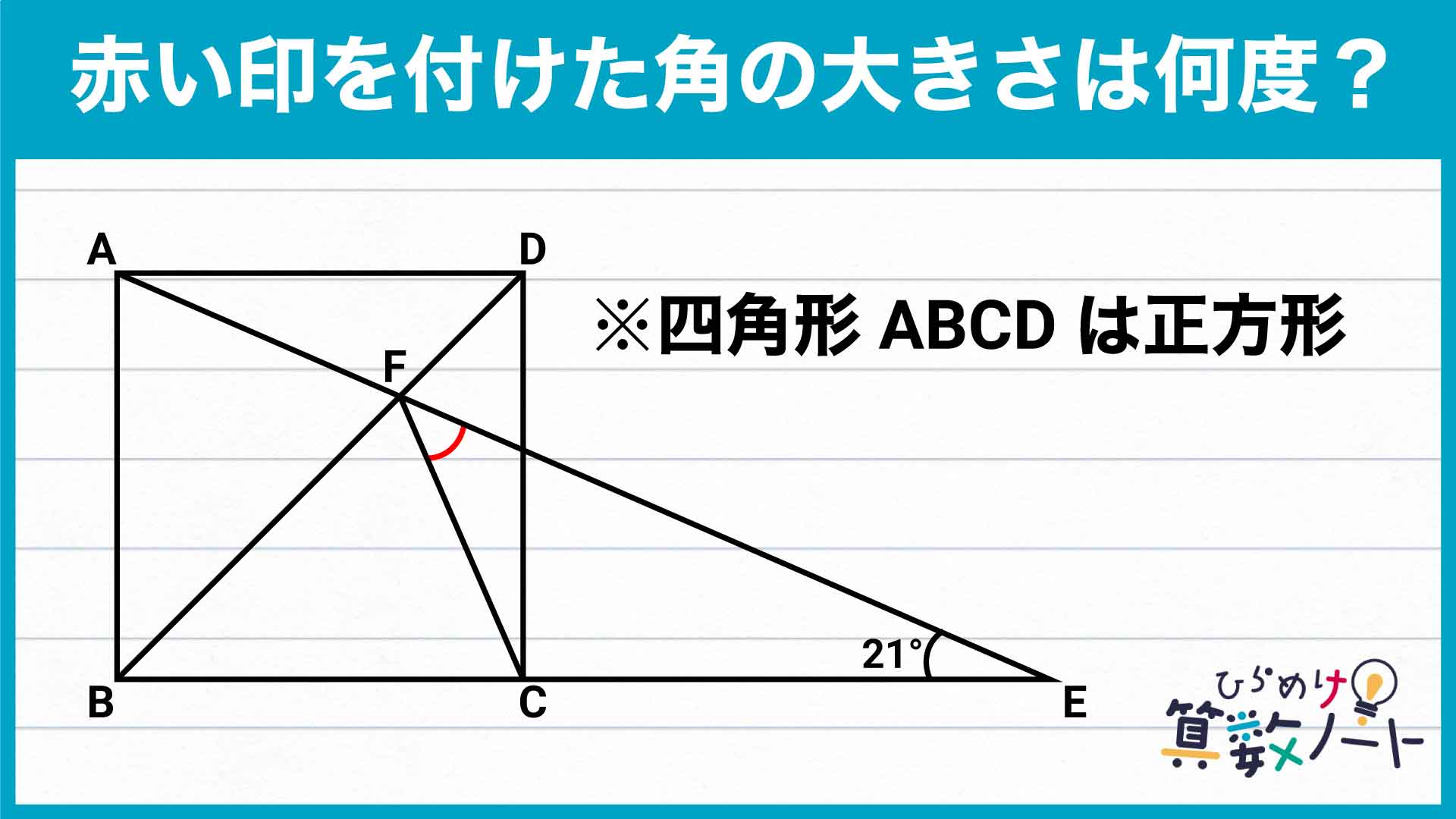
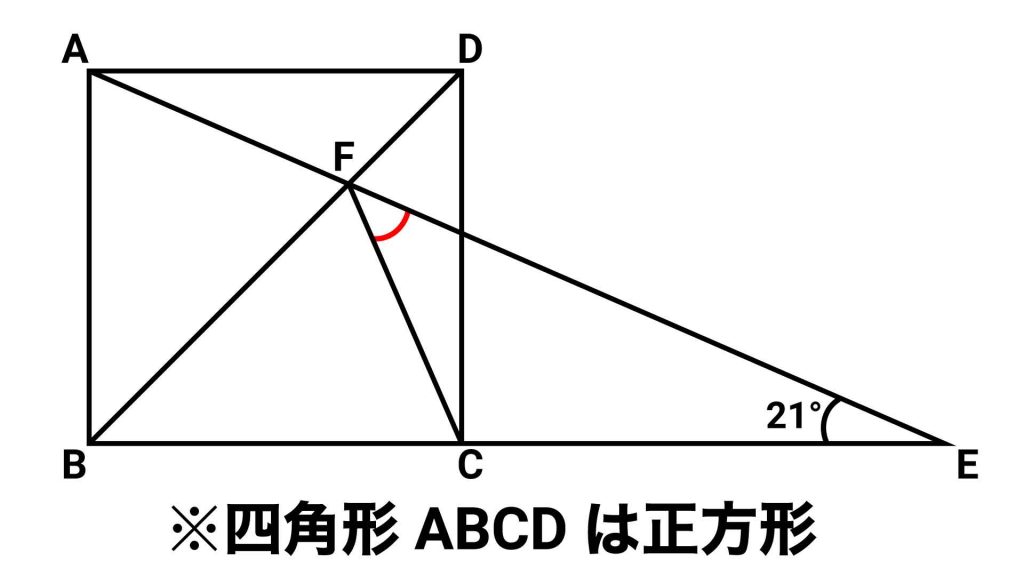
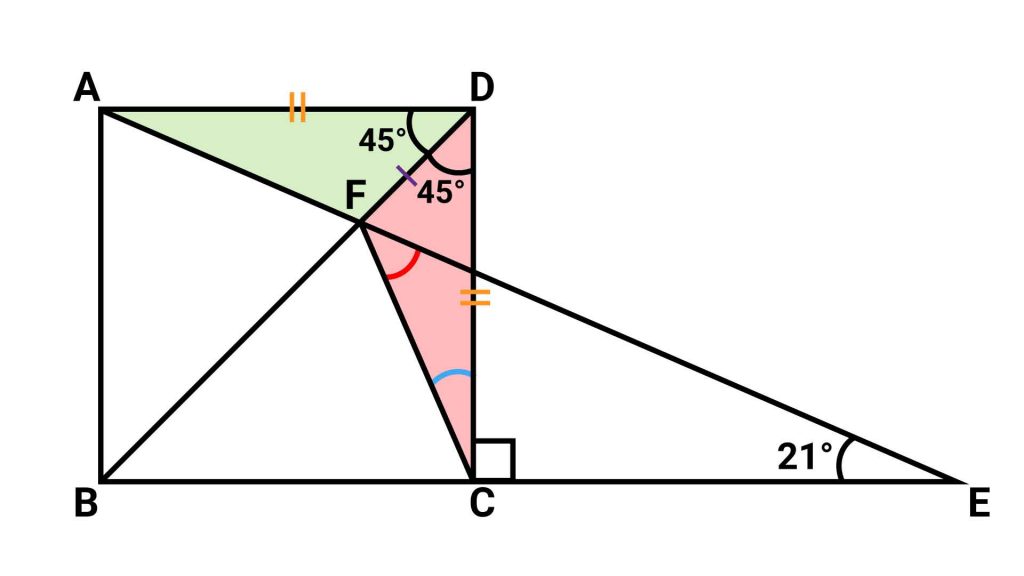
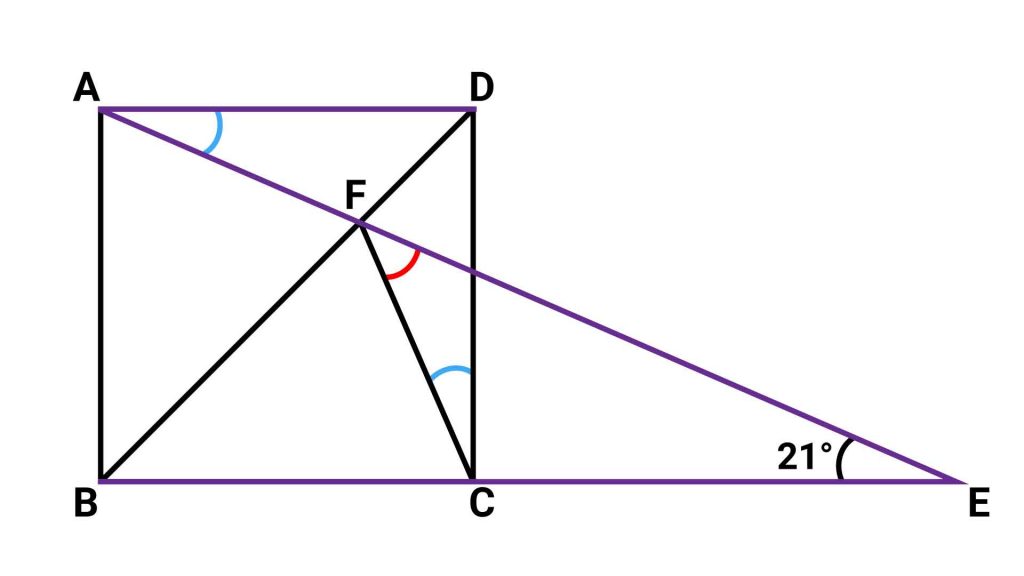
赤い印をつけた角の大きさを求めるにあたり、どの角の大きさがわかればいいかを考えます。ここで着目するのは、三角形FCEです。
角AECの大きさは21度、角DCEの大きさは90度なので、角DCFの大きさがわかれば、三角形の内角の和が180度であることを使って赤い印をつけた角の大きさを求めることができます。
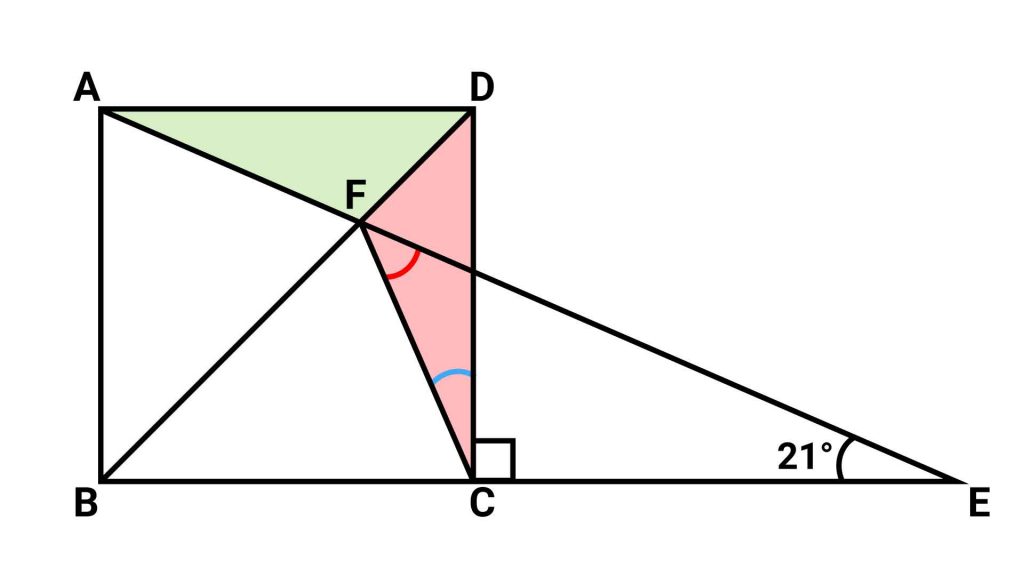
ポイント1:合同な三角形に着目する
ここで、三角形ADFと三角形CDFに着目します。
この2つの三角形は、
- 角ADF=角CDF=45度(BDが正方形ABCDの対角線であるため)
- AD=CD(正方形ABCDの辺の長さはすべて等しいため)
- DFを共有している
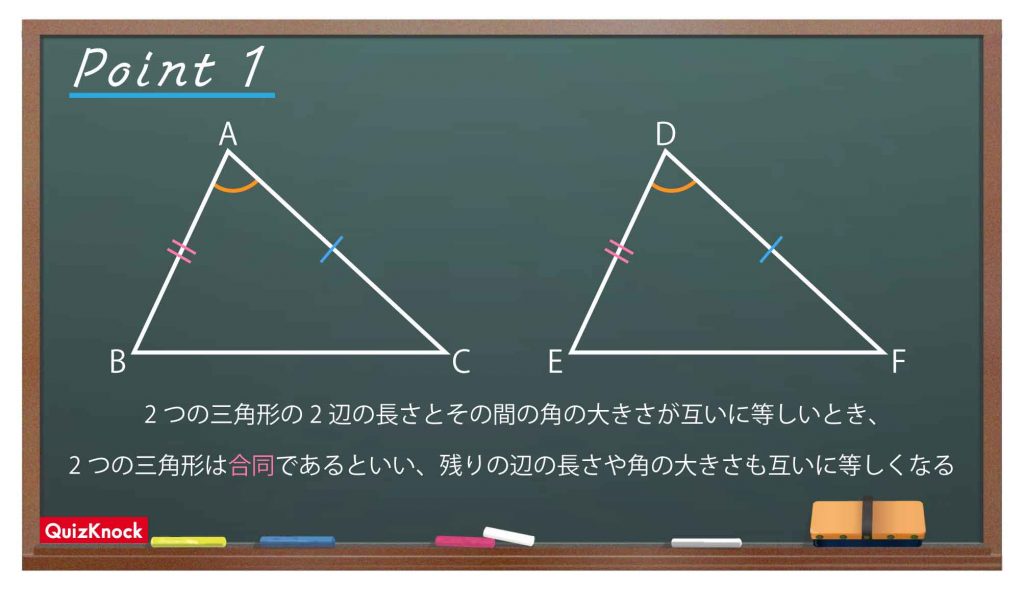
が成り立っており、2つの三角形の2辺の長さと、2辺に挟まれた角の大きさが互いに等しくなっています。
このとき、以下の重要な性質が成り立ちます。
ちなみに、2つの三角形が合同であることを記号で表現するときには、「△ABC≡△DEF」と表現します。
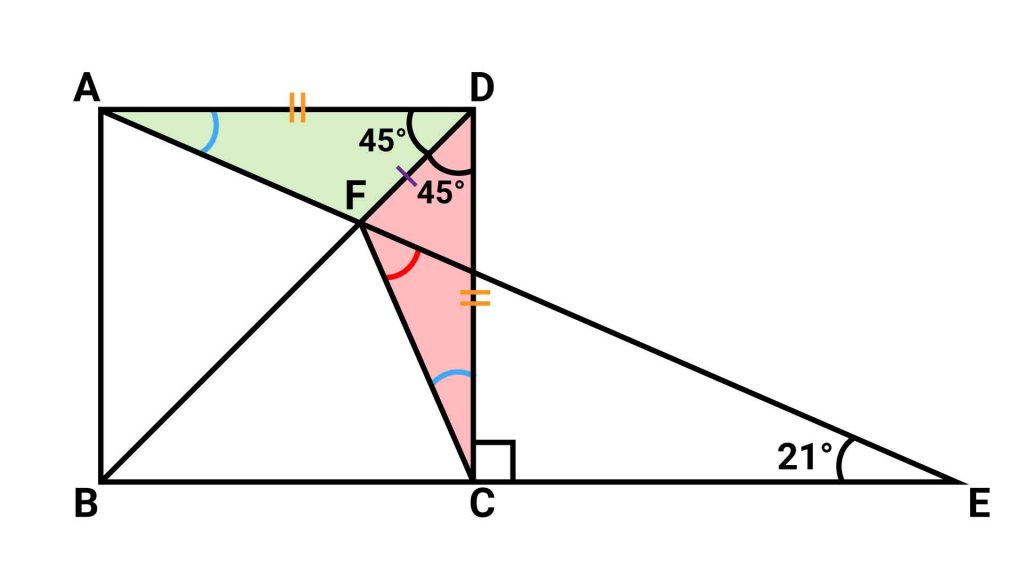
三角形ADFと三角形CDFは、DFを軸として対称な位置にあるため、角DCFと角DAFの大きさが互いに等しくなります。
したがって、答えを出すのに必要な情報は、角DAFの大きさということになります。
ポイント2:角DAFの大きさと同じ大きさを持つ角を探す
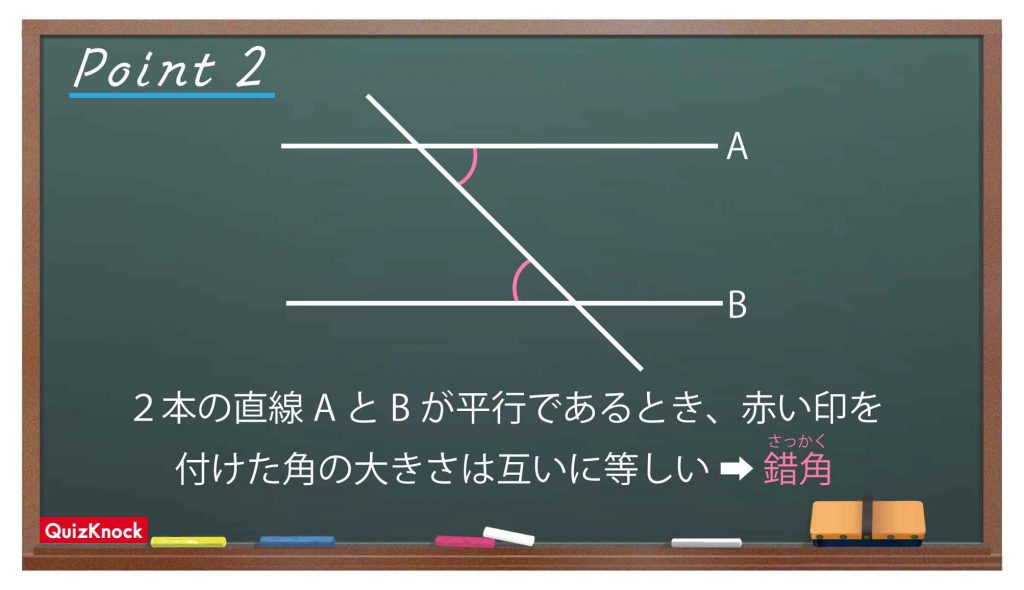
角DAFの大きさを求めるにあたり、以下の重要な性質を使います。
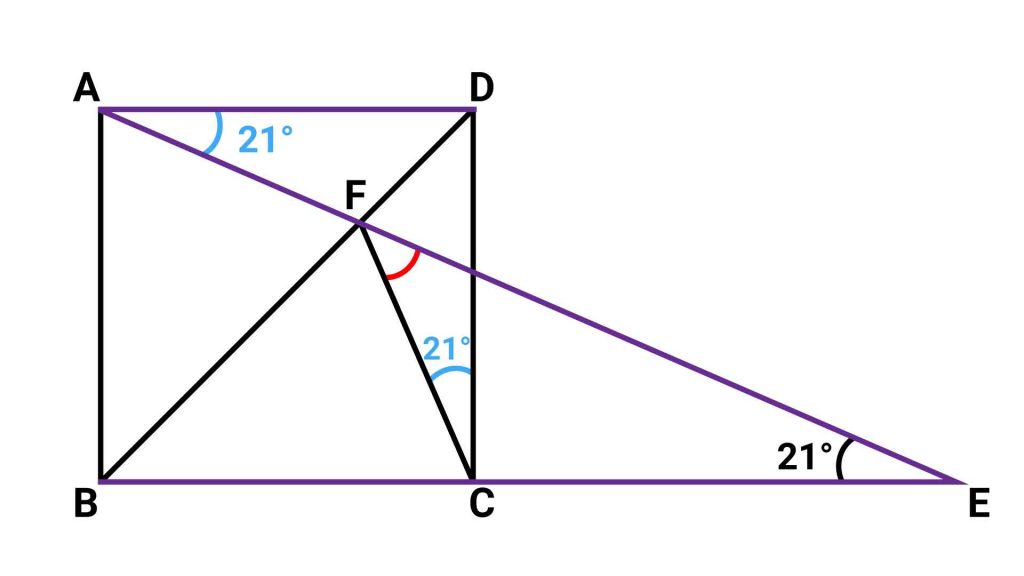
設問の図を見てみると、ADとBEが平行になっていて、AEがその2本の線分を横切るような形になっており、ちょうど上記のPointの図と同じような構造になっています。
したがって、角DAFの大きさは、角AEBの大きさと同じ21度となります。そして、角DAF=角DCFから、角DCFの大きさも21度となります。
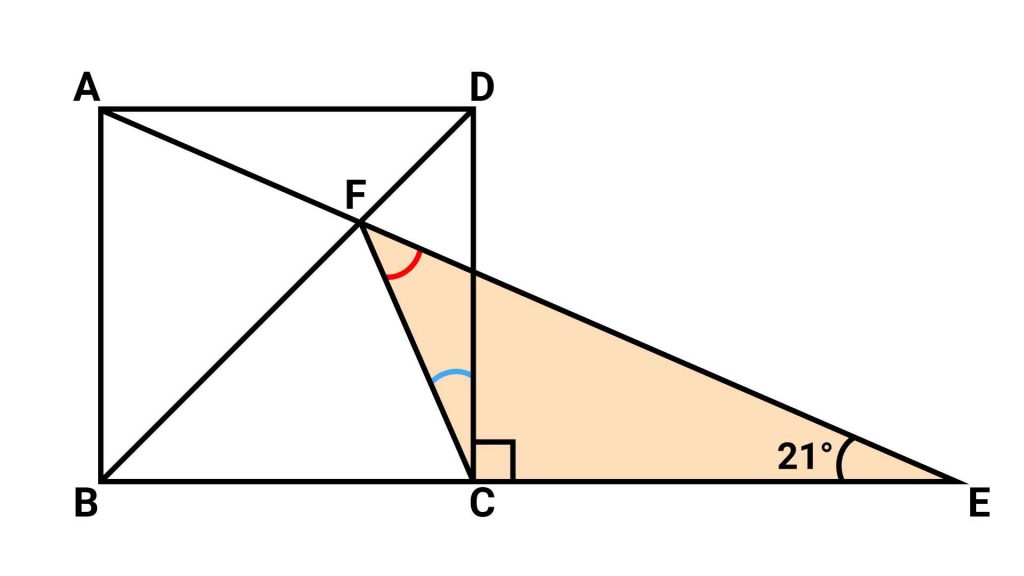
再び、三角形FCEに着目する
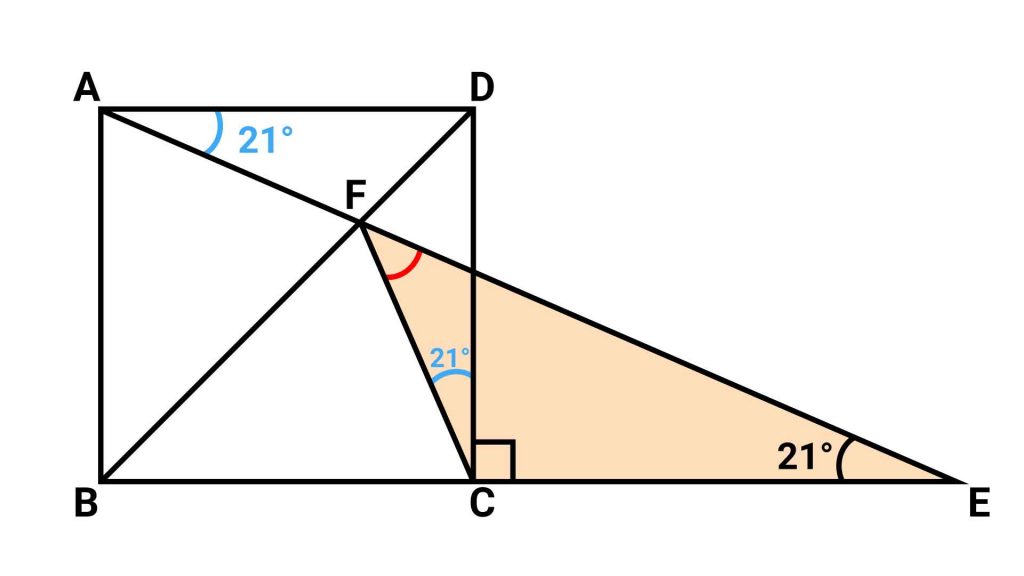
必要な情報が得られたので、再び三角形FCEに着目します。
赤い印の角の大きさは、三角形の内角の和である180度から、角DCF、角DCE、角AECの大きさを引くことで求められるので、180-(21+90+21)=48度となります。
答え:48度
合同な三角形があることに気付けるかどうかが、この問題のポイントでした。
それでは。
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)








.jpg)






