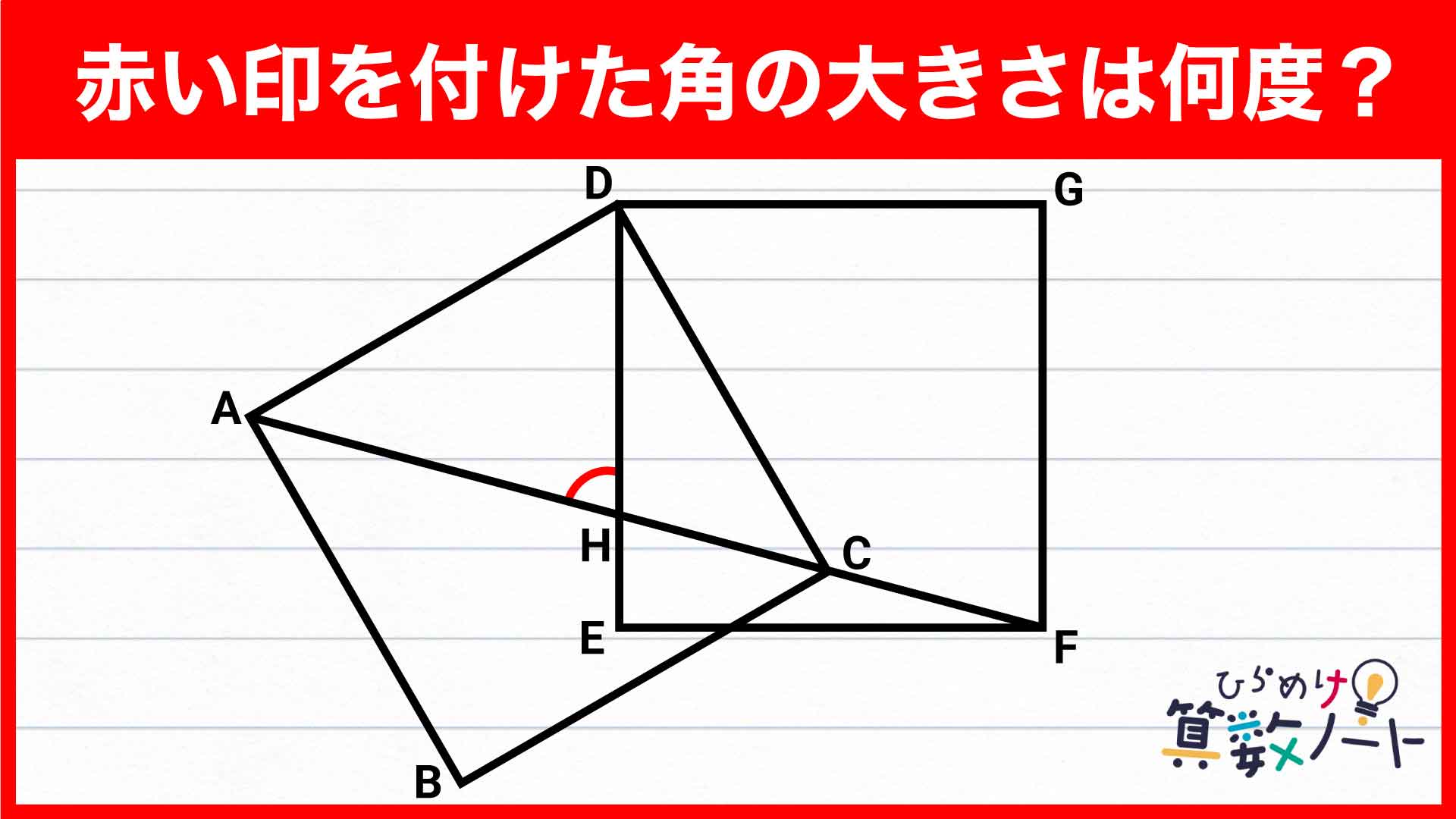
解説
それでは解説です。この問題についてはさまざまな解き方がありますが、ここでは「小学5年生で解ける」解き方を紹介します。
前ページ：【回答フォーム】自力で解きたい方はこちらへ！ 以下は問題の答えです。
ご無沙汰しております。今回は僕と一緒に解いていきましょう！
ヒントとなった補助線はこちら！
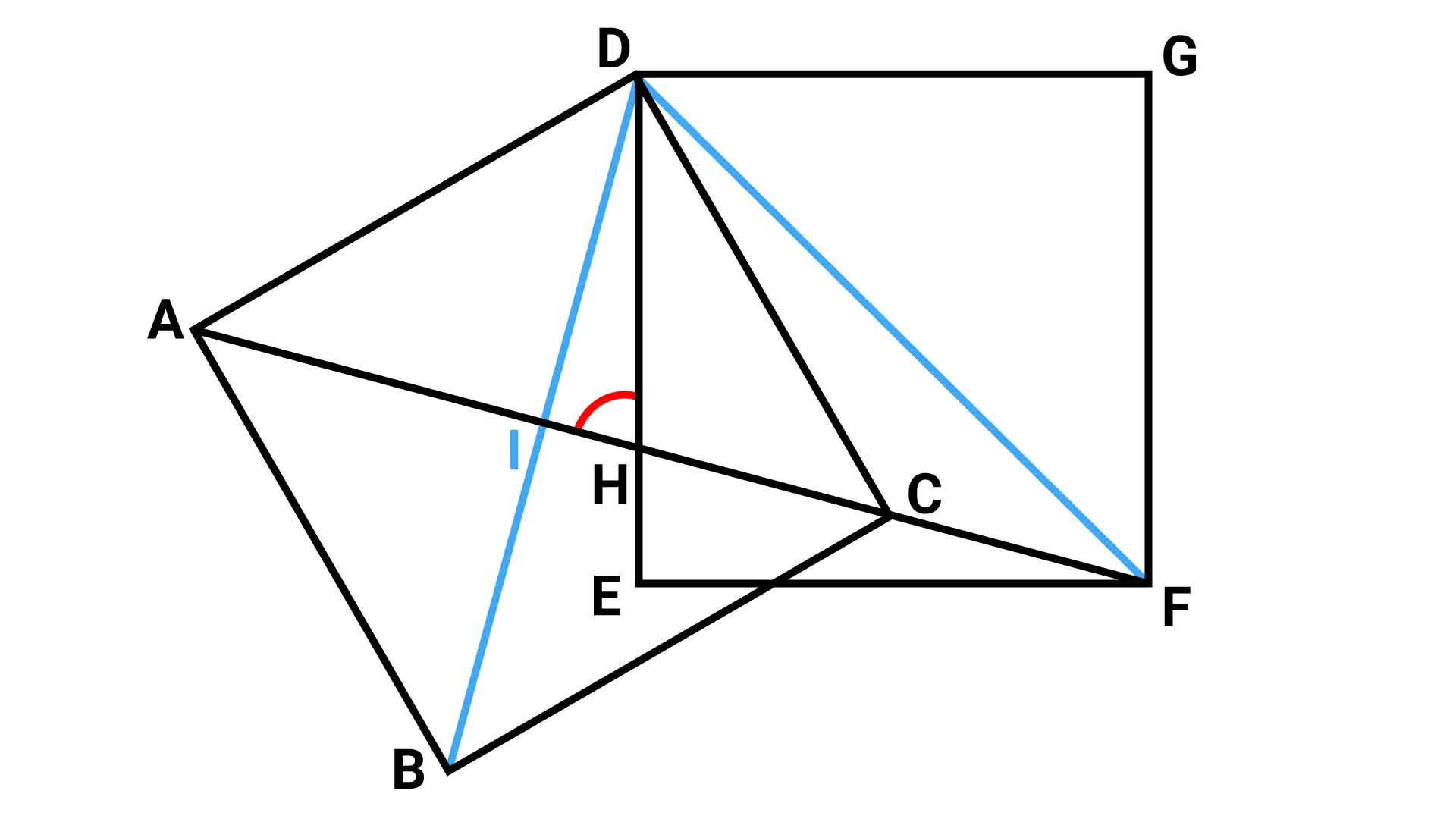
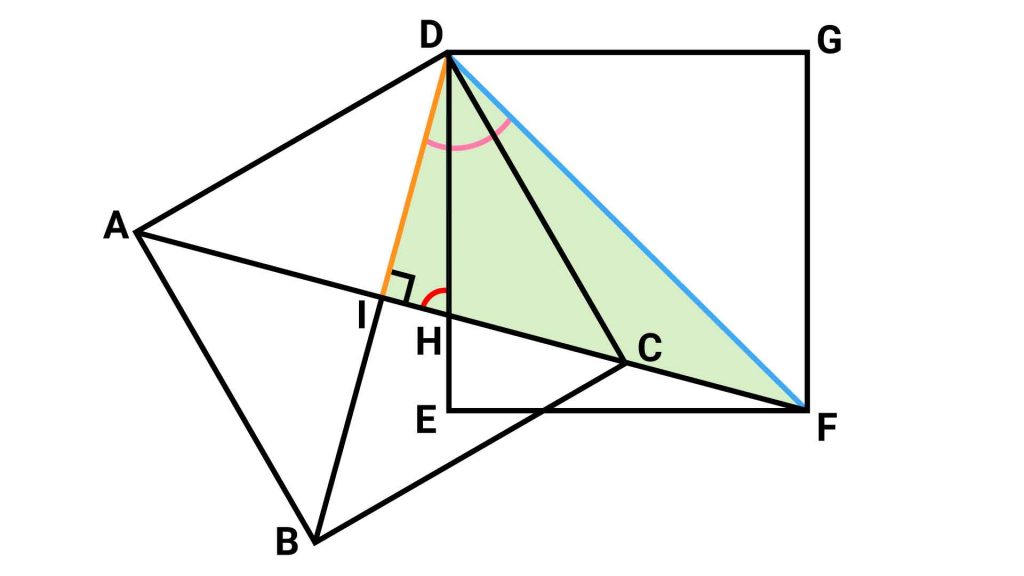
補助線を、以下の図のように2本引きます。
【1本目】DとBを結ぶ（正方形ABCDの対角線）
【2本目】DとFを結ぶ（正方形DEFGの対角線）
▲対角線を2本引きました。ここからどうする？
いったん、ゴールから逆算して考えてみます。
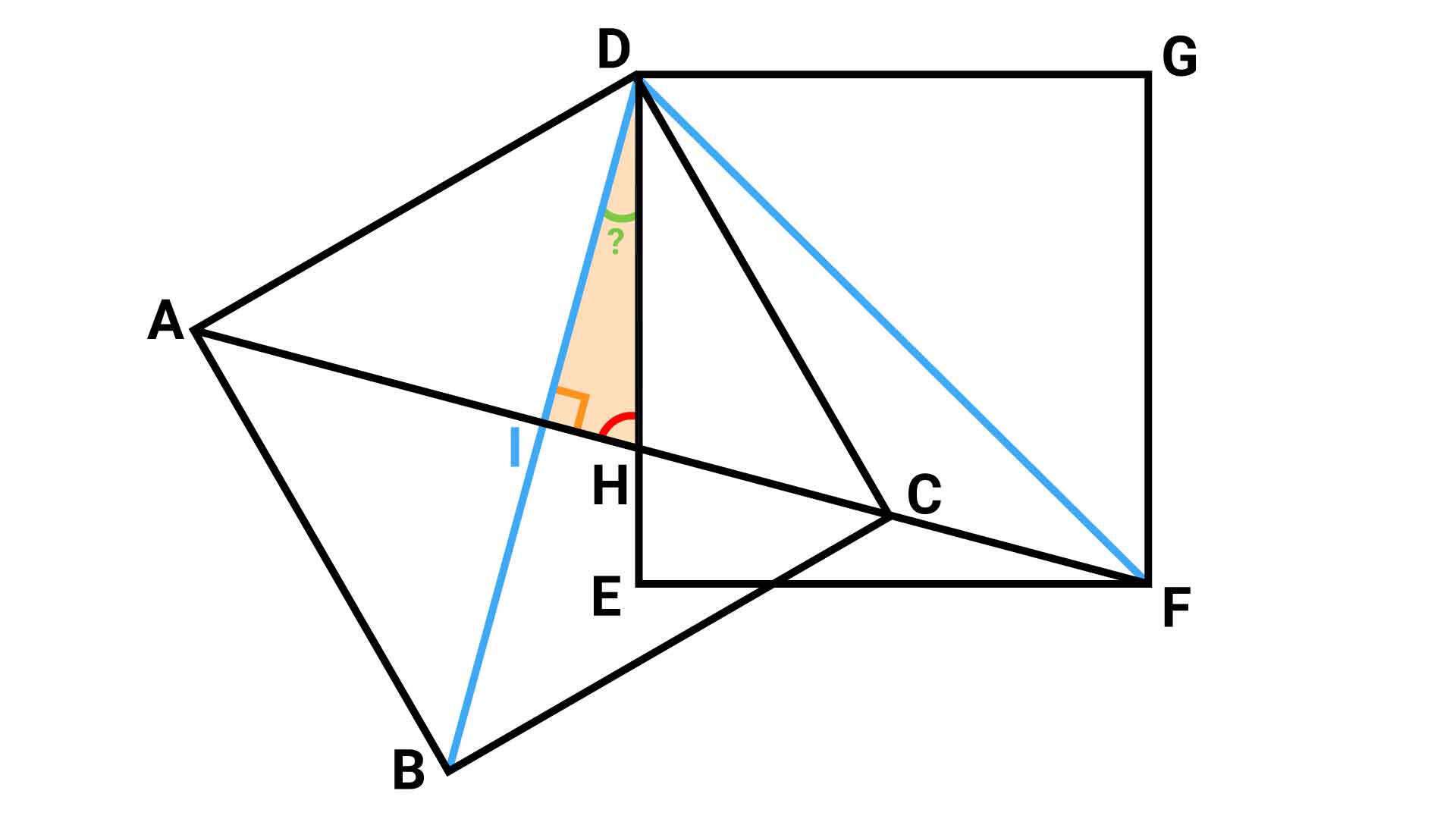
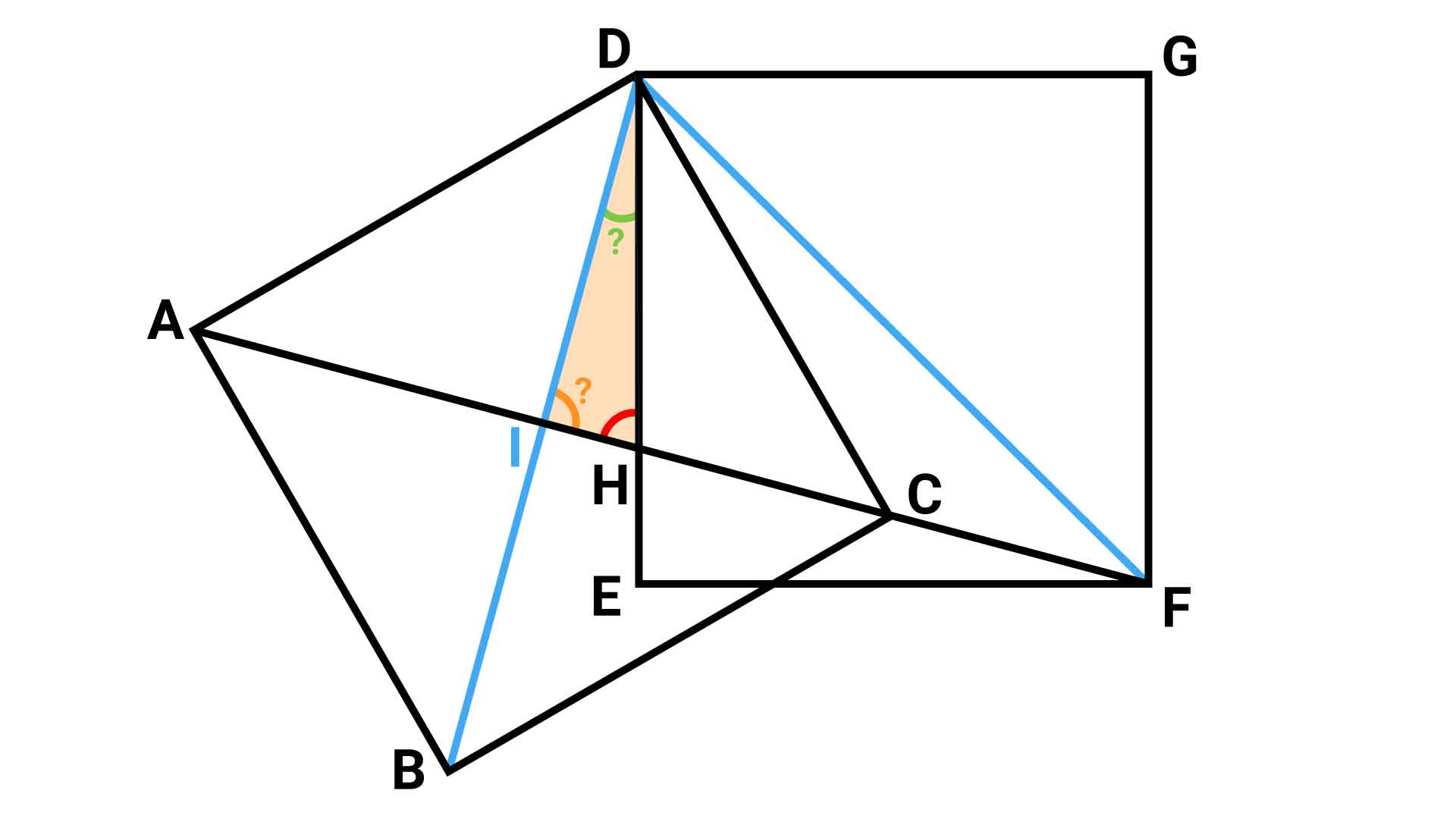▲緑とオレンジの角の大きさがわかれば、赤い印を付けた角の大きさがわかる。
三角形DIHにおいて、角DIHと角IDHの大きさがわかれば、三角形の内角の和が180度であることを用いて、芋づる式に角DHIの大きさを求めることができます。
2つの角の大きさを、順に求めていきましょう！
角DIHの大きさは、正方形の性質を使って求める
まずは、角DIHの大きさを求めます。ここで、以下の重要な性質を使います。
設問の図が複雑だと、この性質を見落としがちなので注意！
角DIHは、正方形ABCDの対角線ACとBDが交わってできる角なので、角DIH=90度となります。
角IDHの大きさを求める
次に、角IDHの大きさを求めます。
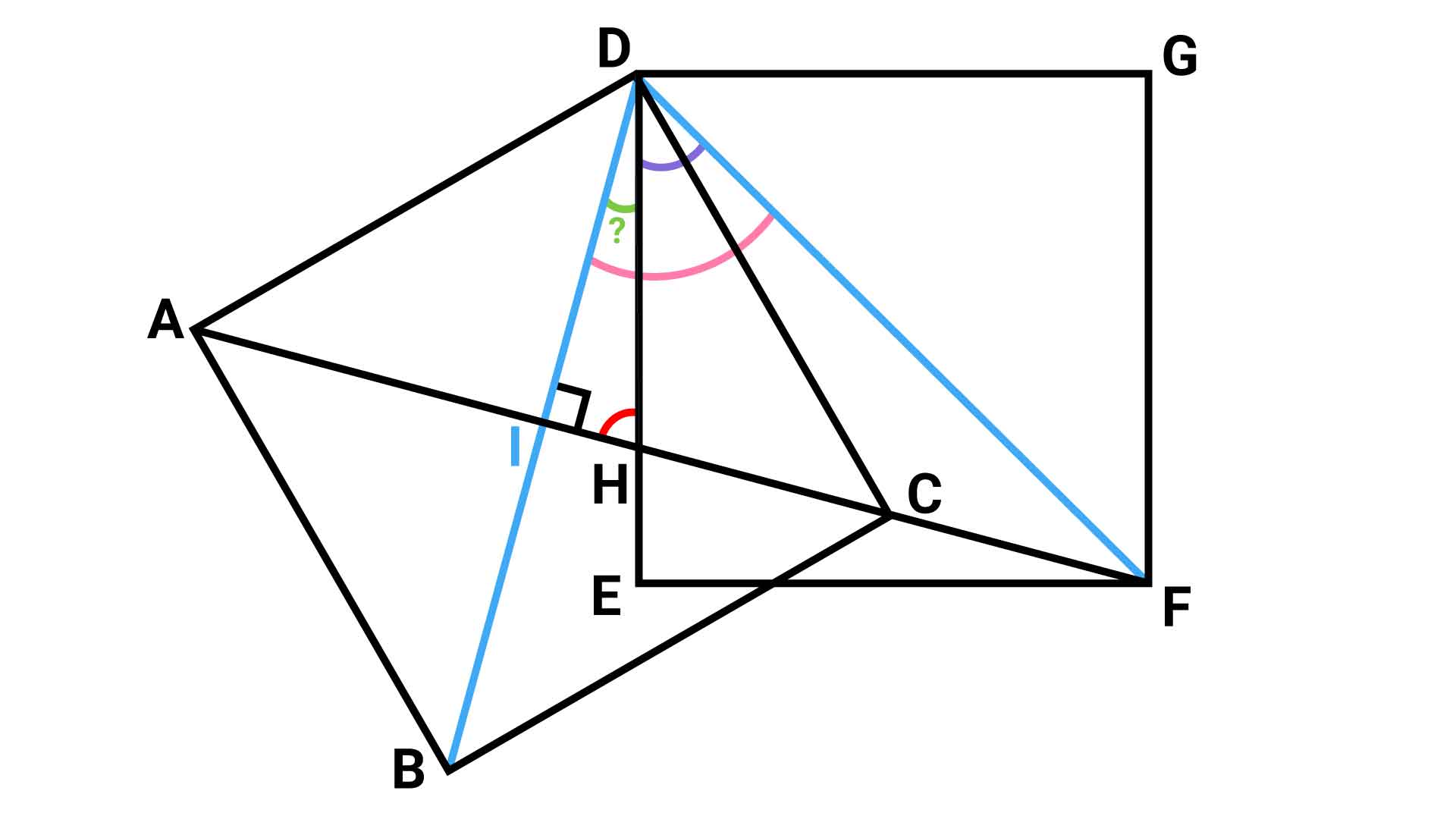
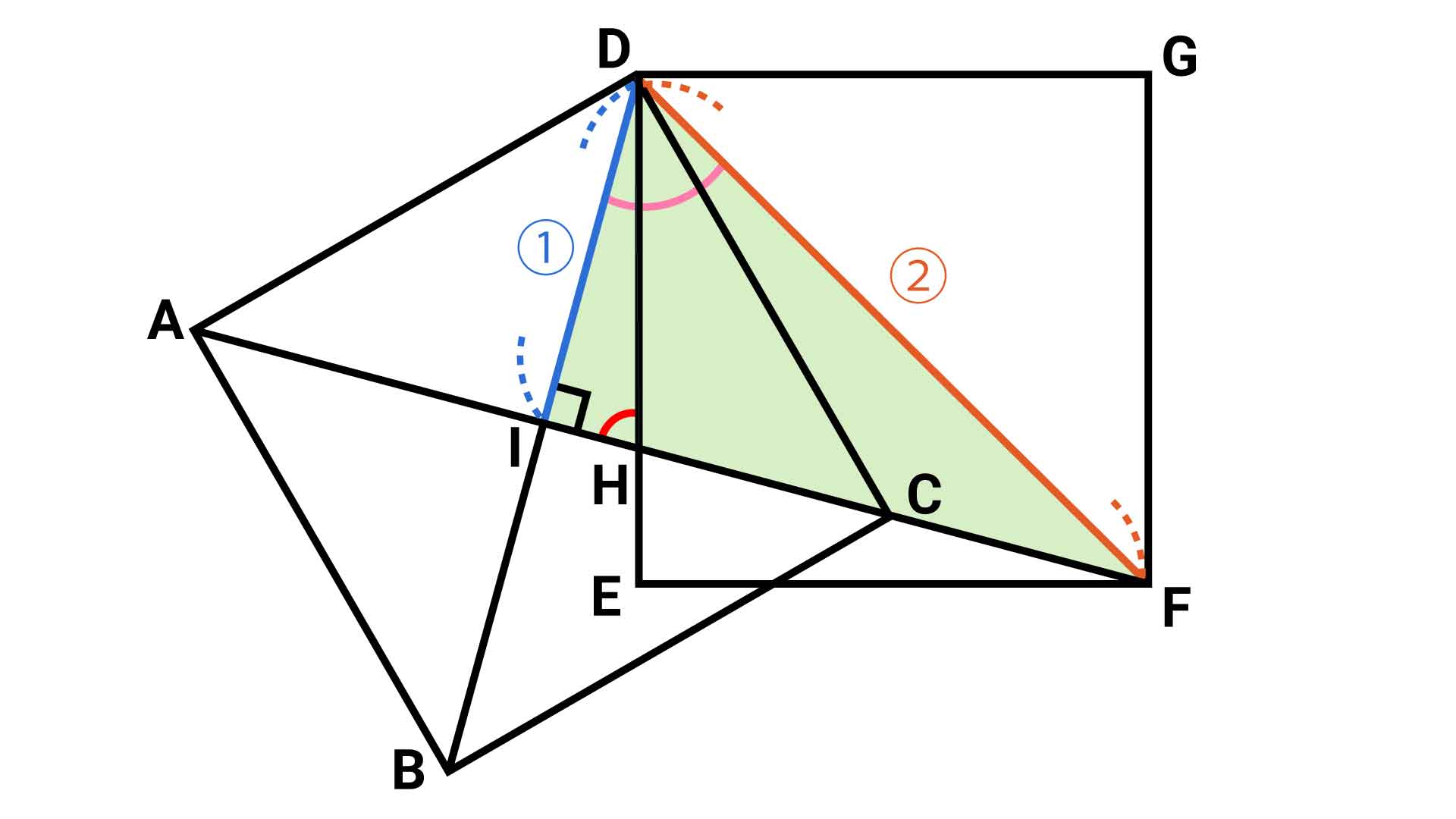
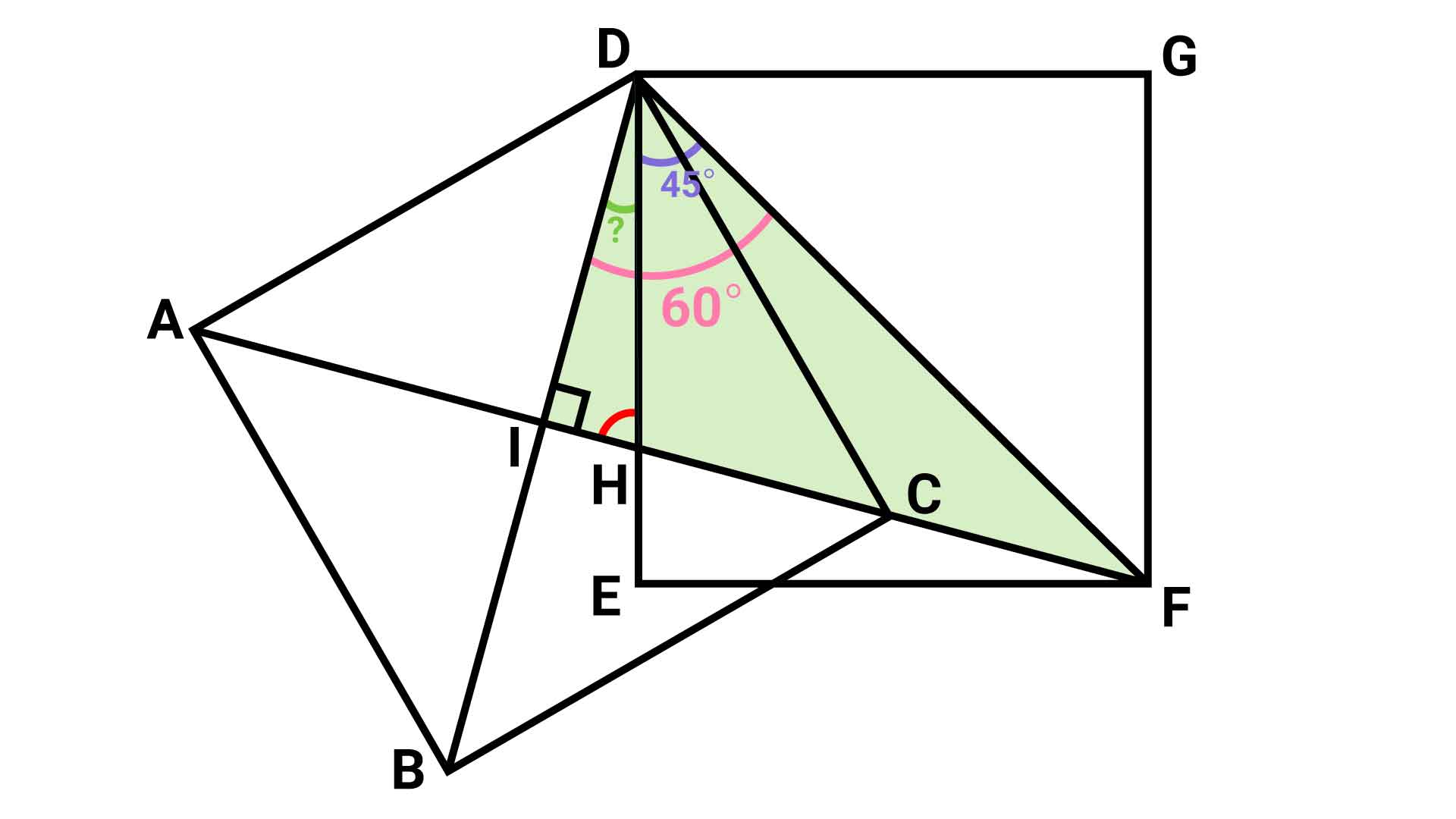
角IDHの大きさを求めるために必要な情報が、角IDFと角HDFの大きさです。この2つの角の大きさがわかれば、（角IDF-角HDF）を計算することで、角IDHの大きさを求めることができます。
角HDFの大きさは？
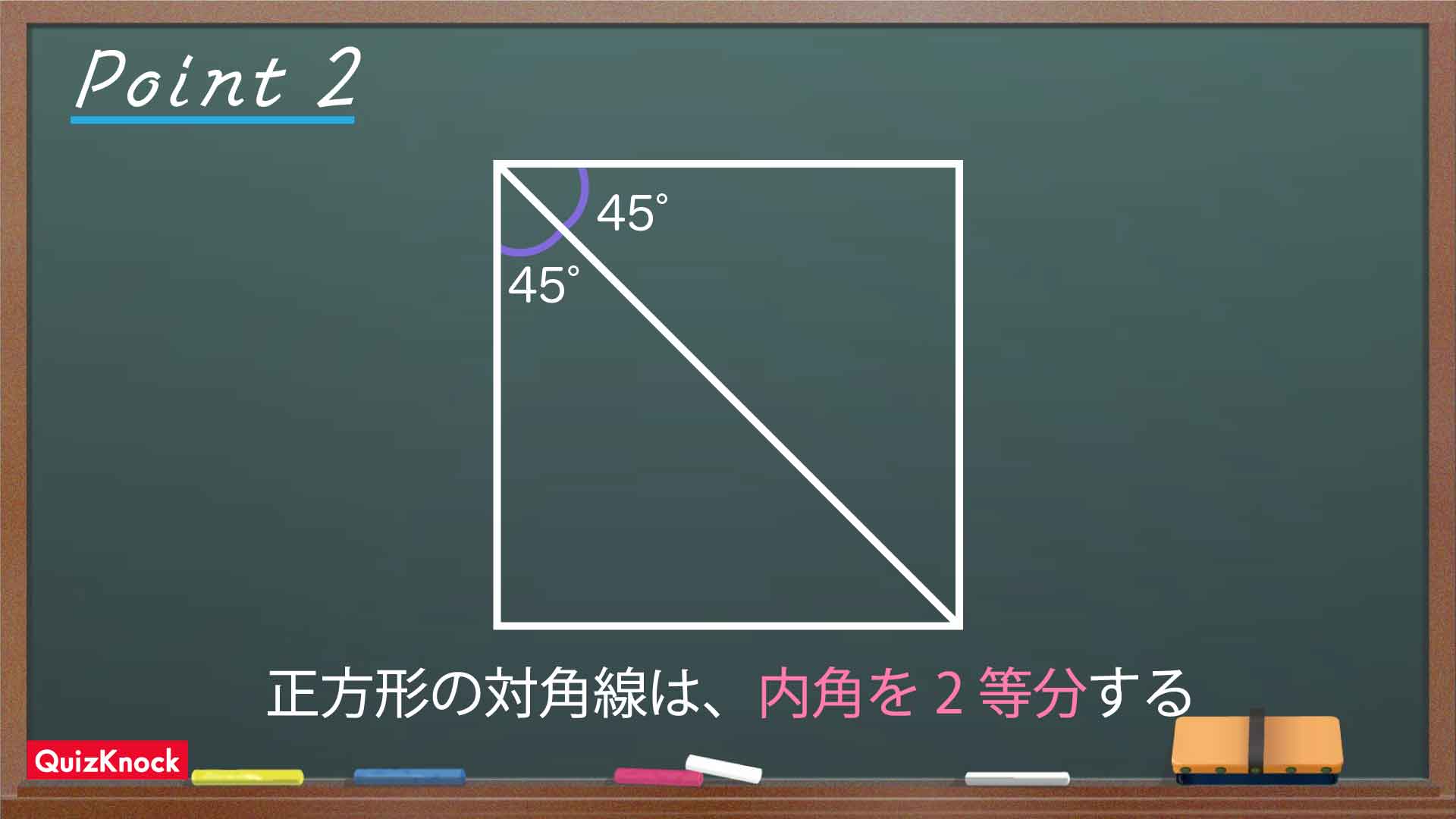
まず、以下の重要な性質を使って、角HDFの大きさを求めます。
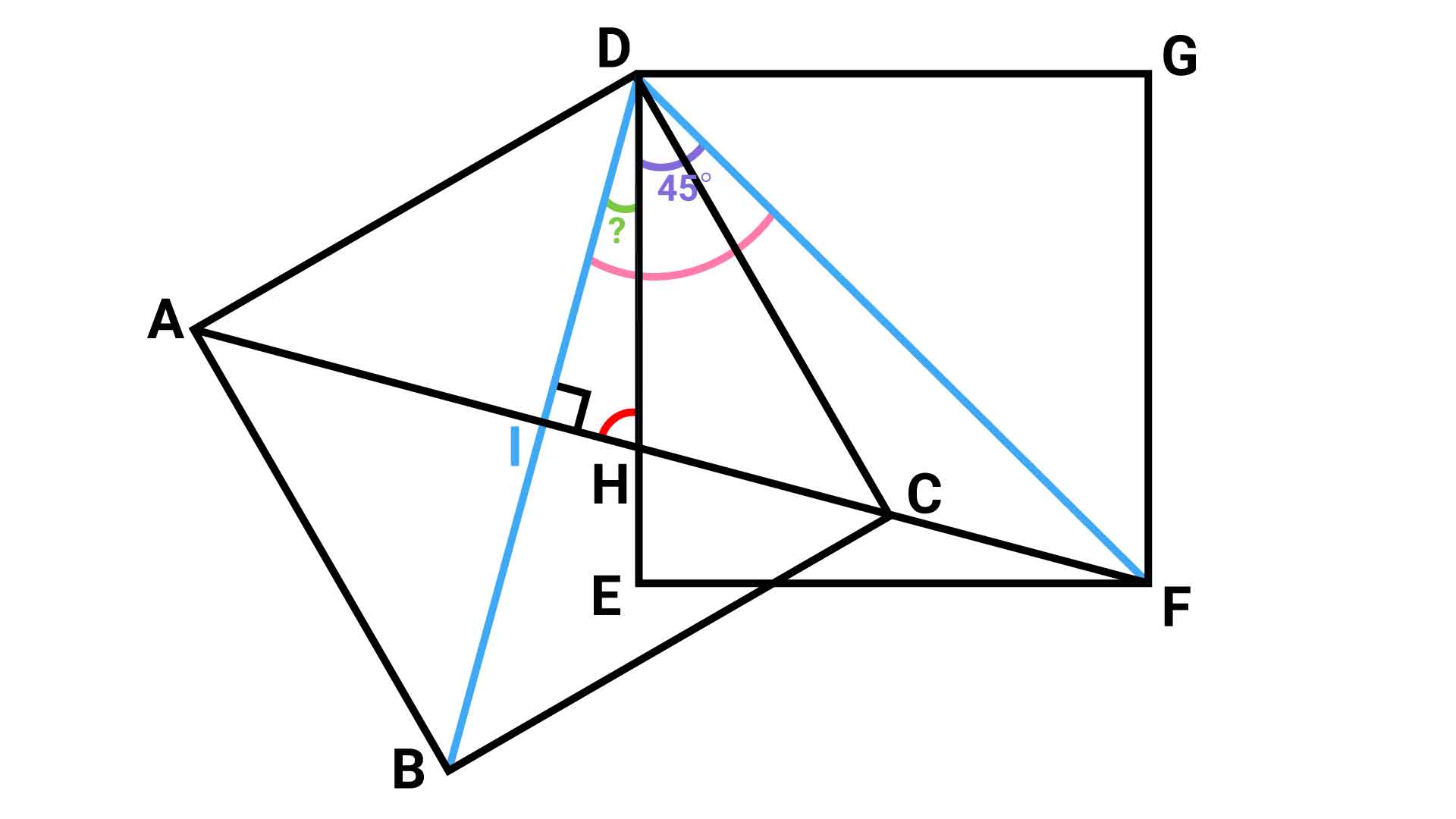
角HDFは、正方形の対角線によって作られる角です。したがって、角HDFの大きさは45度となります。
角IDFの大きさは？
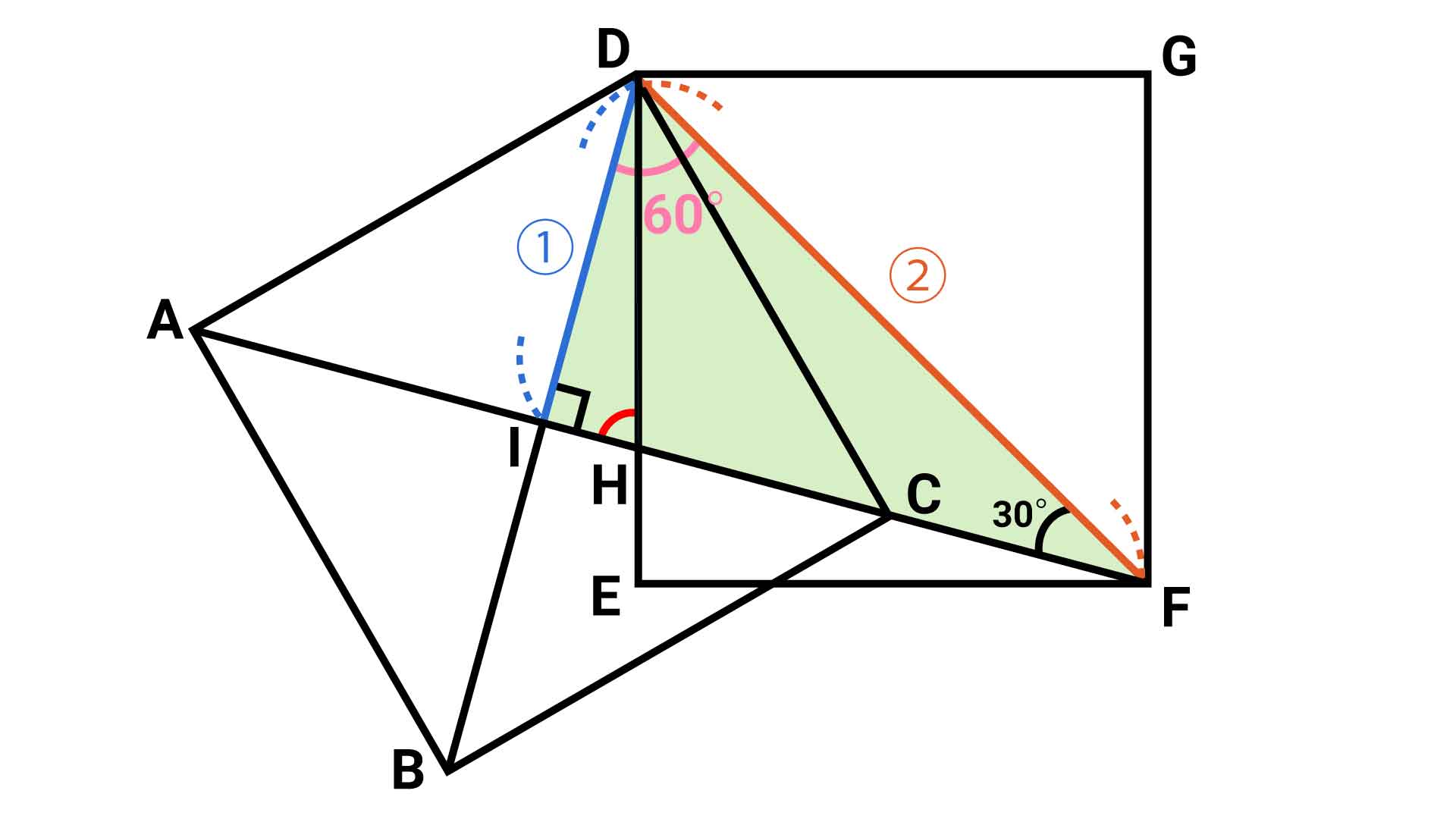
次に、角IDFの大きさを求めます。ここで着目すべきは、直角三角形DIFです。
一見普通の直角三角形ですが、ここから何がわかるのでしょうか？
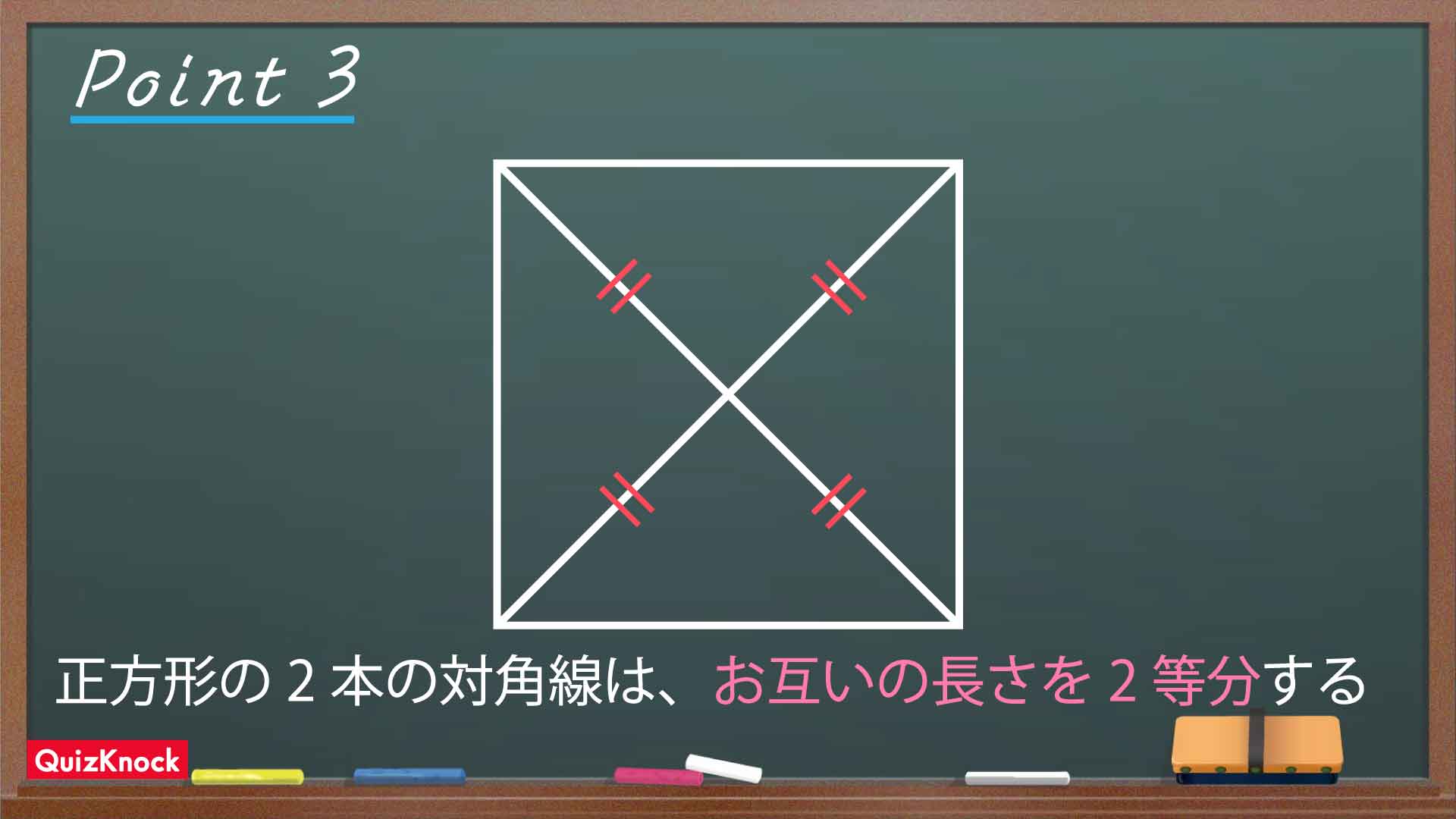
正方形に関する以下の性質を使うと、直角三角形DIFの特徴が見えてきます。
正方形ABCDとDEFGは同じ大きさなので、対角線DBとDFの長さが同じです。上記の性質から、DIの長さはDBの長さの半分なので、DIとDFの長さの比は1：2になります。
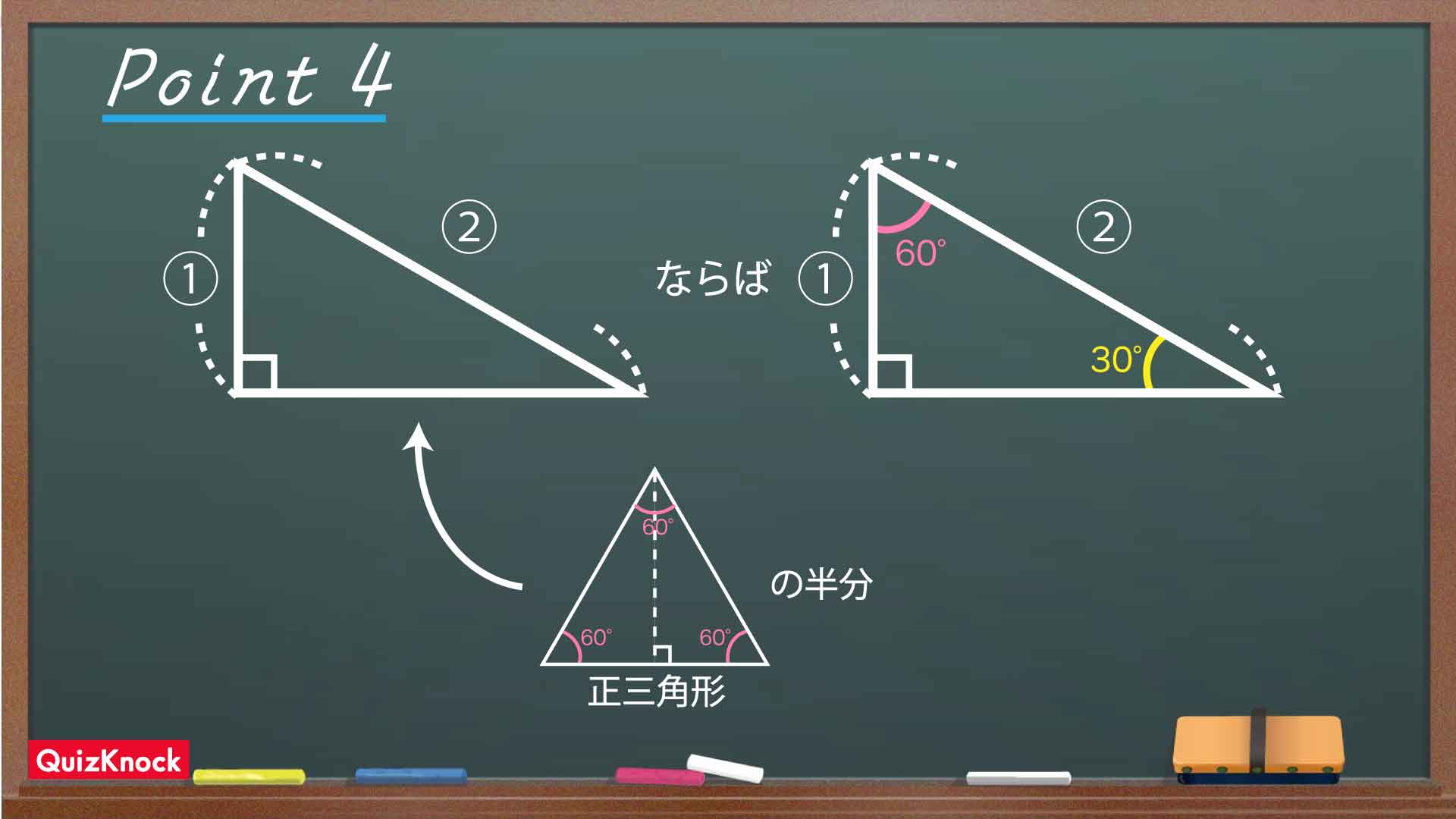
この直角三角形について、以下の性質を使います。
以上の性質から、角IDFの大きさは60度と求めることができます。
ちなみに、IFの長さは、DIの長さの√3倍になります。
役者はそろった
ここまで来れば、あとは計算によって求めるだけです。
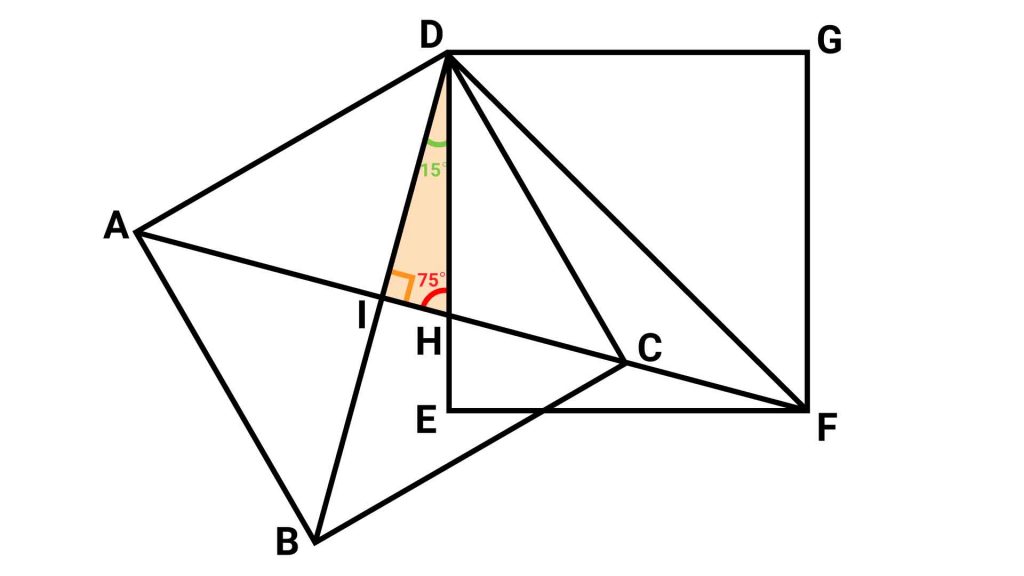
まず、角IDHの大きさは、角IDFの大きさから角HDFの大きさを引くと求められるので、60-45=15度です。
最後に、角DHIの大きさは、三角形の内角の和から、角IDH、角DIHの大きさをそれぞれ引くと求められるので、180-15-90=75度となります。
答え：75度
今回もかなりの長旅でしたね…… お疲れさまでした！
隠された直角三角形を見つけ出せるかが、この問題のポイントでした。
それでは。
【前回の超難問はこちら】 【前回の算数ノートはこちら】 【あわせて読みたい】
