解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
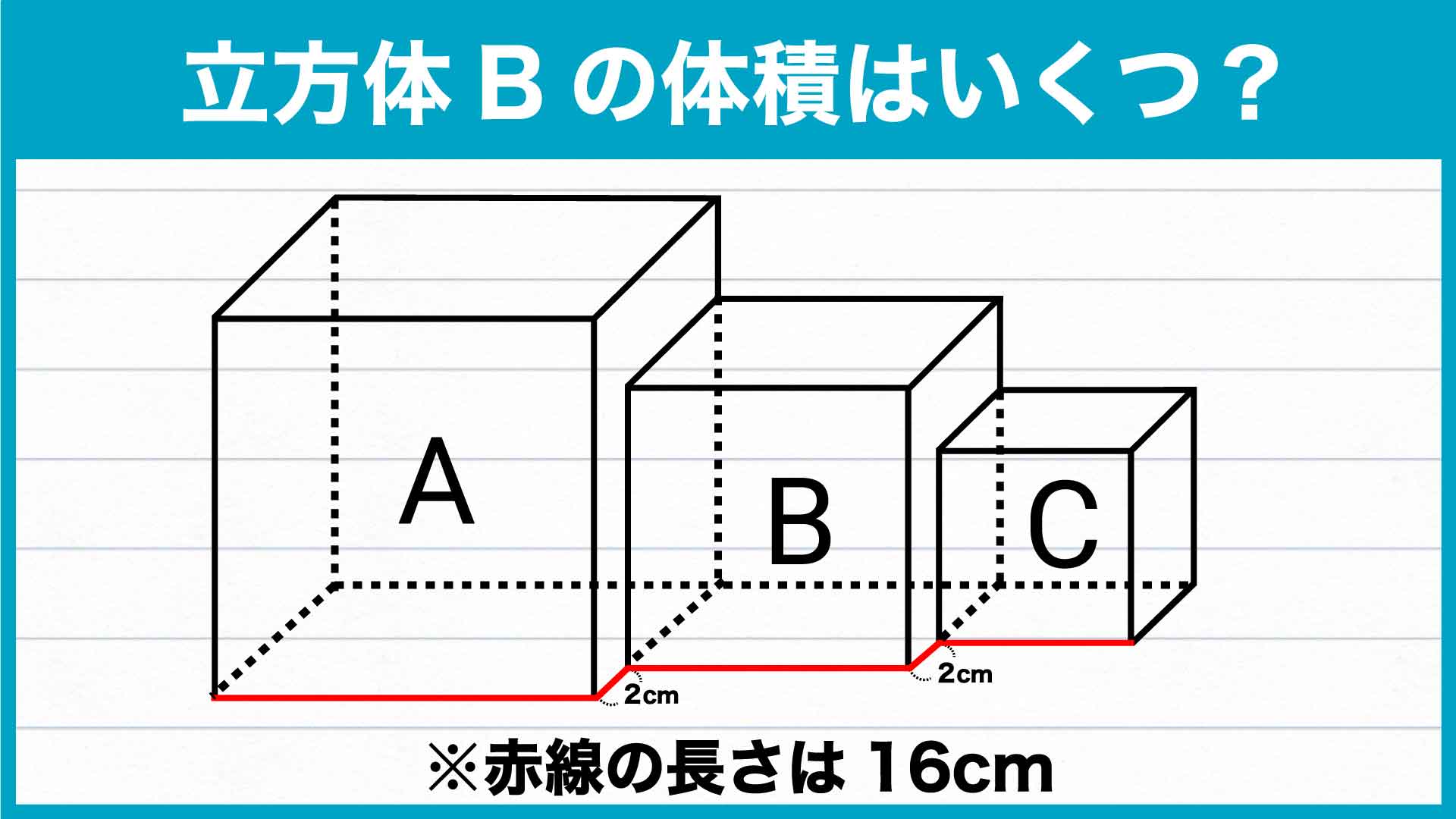
立方体Bの体積を求めるには、立方体Bの一辺の長さを求める必要があります。その長さをどのように出すかが、この問題最大の壁です。
赤線をピンと伸ばすと、下の図のような内訳になっています。
立方体A、Cそれぞれの一辺の長さと、立方体Bの一辺の長さの関係がわかるといいのですが……。
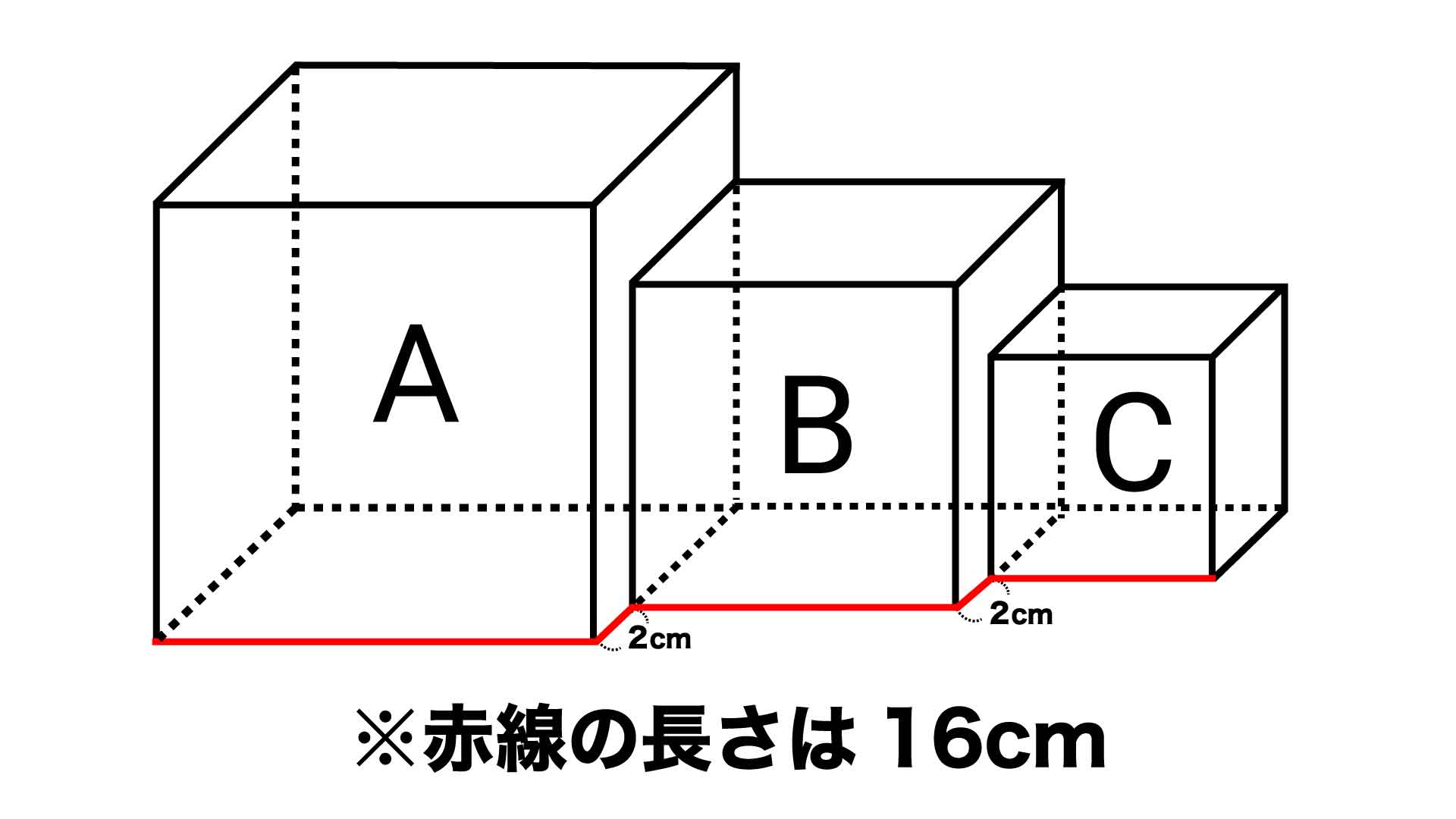
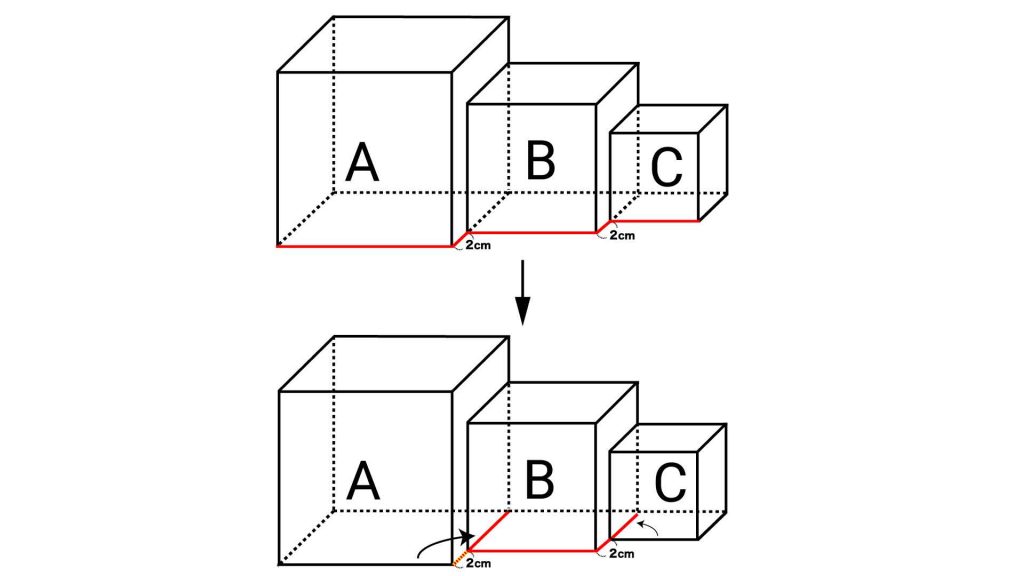
それぞれの辺の関係を知るために、赤線を「立方体Bの辺に沿う」ように移動させます。
赤線を移動させる
では、早速赤線を移動させていきましょう。図とともに説明していきます。
立方体は全ての辺が同じ長さなので、立方体Cの一辺についている赤線は、Bと接している辺に移動できます。
同様に、立方体Aの一辺についている赤線も、Bと接している辺に移動できます。このとき、立方体Aの一辺のうち、2cmだけが立方体Bの外にはみ出します。
▲少しわかりにくいですが、オレンジの線がはみ出した部分です
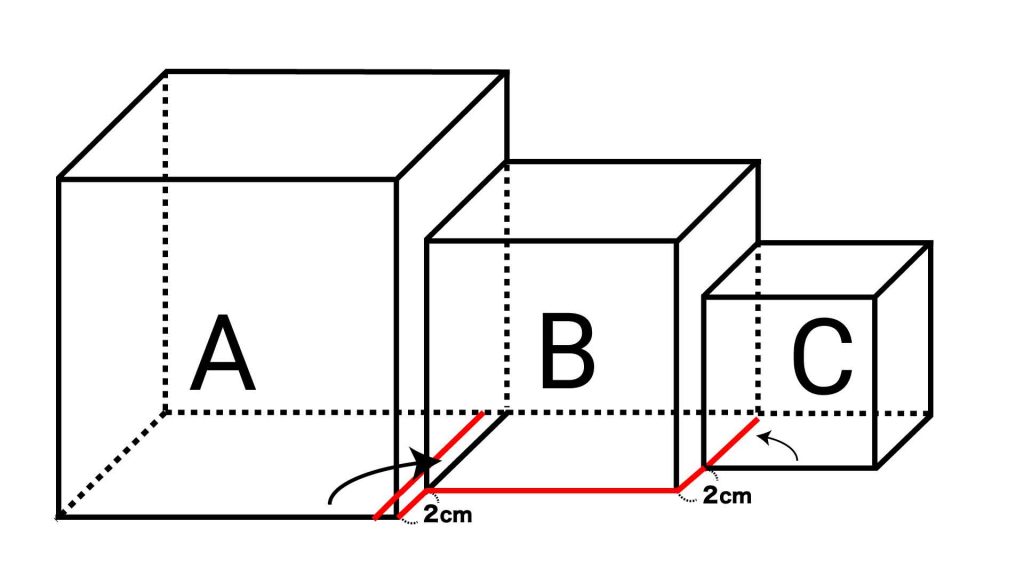
「わかりにくいよ！」という方のために、拡大して、赤線を少しずらした画像を用意しました。
この図から、立方体Aの一辺は立方体Bの一辺に2cm足した長さと同じということがわかります。また、立方体Cの一辺に2cm足すと、立方体Bの一辺の長さになります。
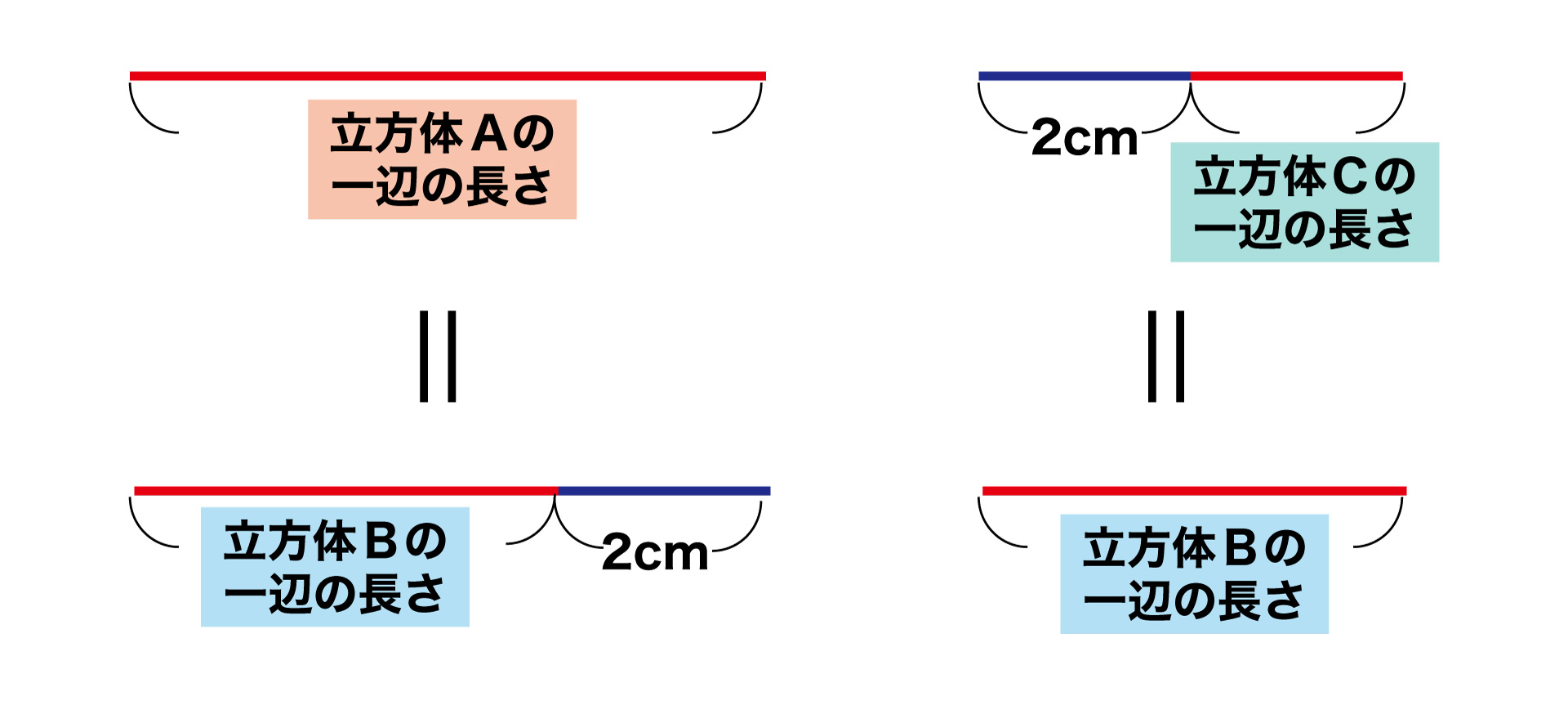▲立方体A、Cの一辺の長さは立方体Bの一辺の長さで表すことができる！
これで赤線の内訳を立方体Bの一辺の長さで表すことができそうです！
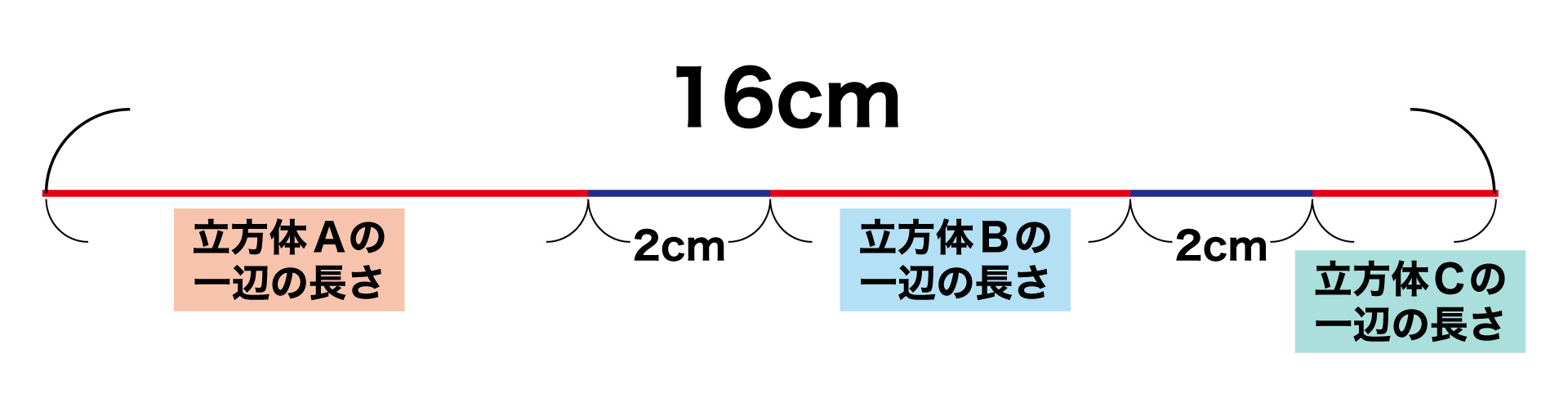
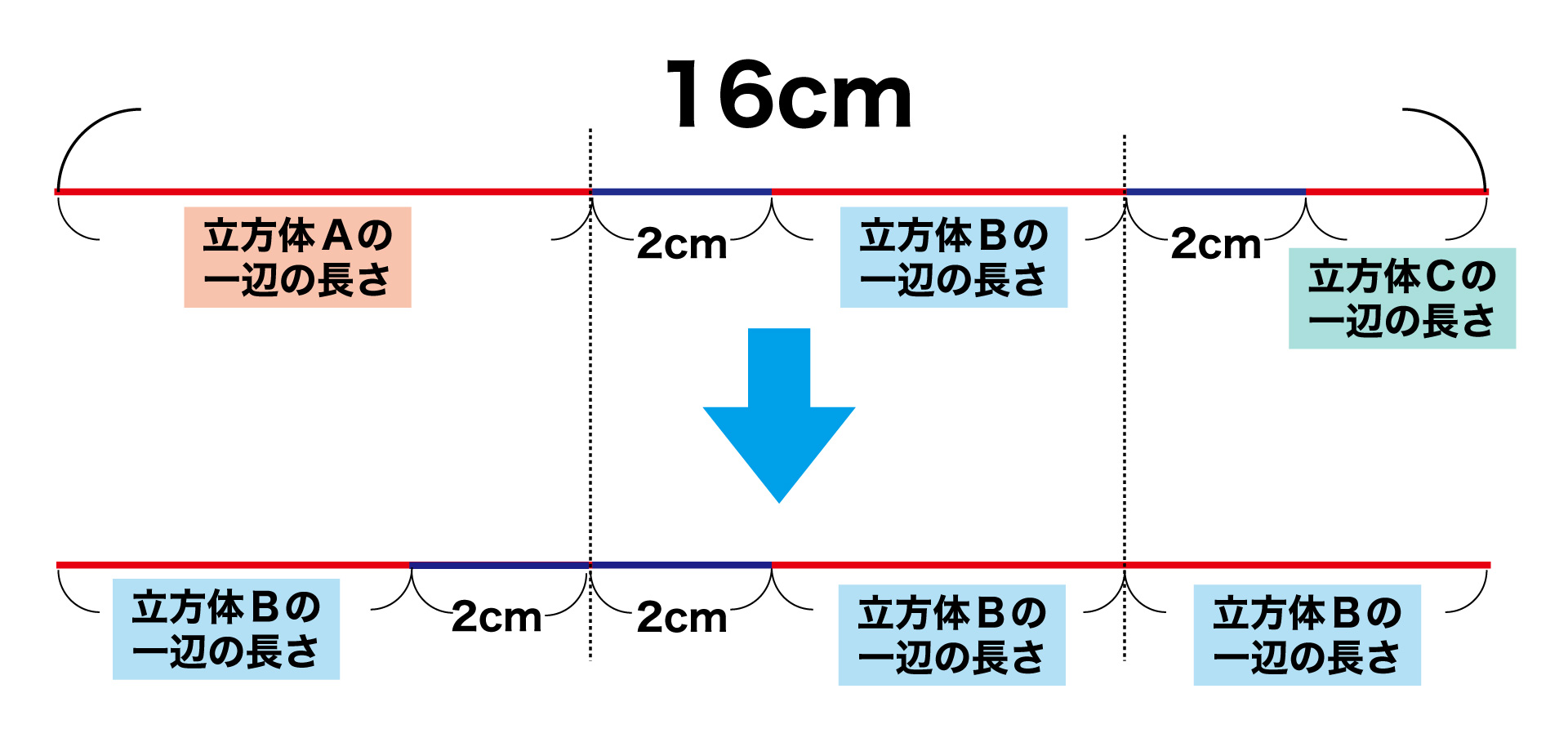
これらのことをまとめると、16cmの赤線は以下のように表すことができます。
したがって、赤線から2+2=4cmを引いた12cmが、立方体Bの3辺分の長さとなります。
つまり、立方体Bの一辺の長さは12÷3=4cmです。以上より、求める立方体Bの体積は4×4×4＝64cm3となります。
答え：64cm3
赤線を立方体Bの一辺の長さで表すことができるかがカギとなる問題でした。
おまけ
実はこの問題、算数シリーズの第1回で出題した問題の類題となっています。
その問題がこちら！
こちらの問題にもぜひ挑戦してみてください。
それでは。
【あわせて読みたい】
