小学6年生で解ける「長方形の面積」の問題、あなたは解ける？

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

前ページ：【解答フォーム】自力で解きたい方はこちらへ！　以下は問題の答えです

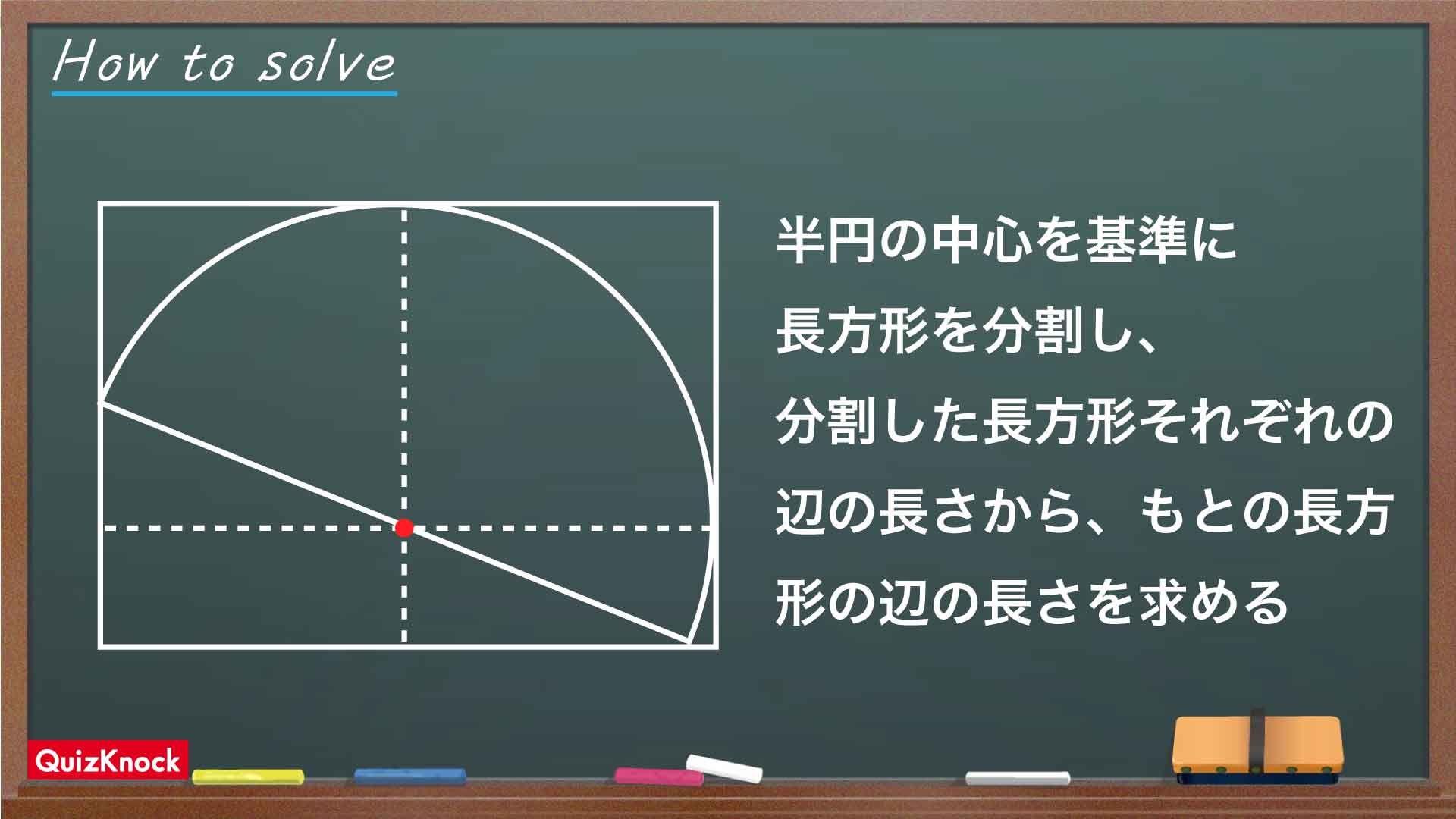
今回の解き方をまとめた図がこちらです。

今回のポイントは、「図形の性質を活用し、長方形の辺の長さを求める」ことです。

この流れに沿って問題を攻略していきましょう！

長方形の中に線を引く

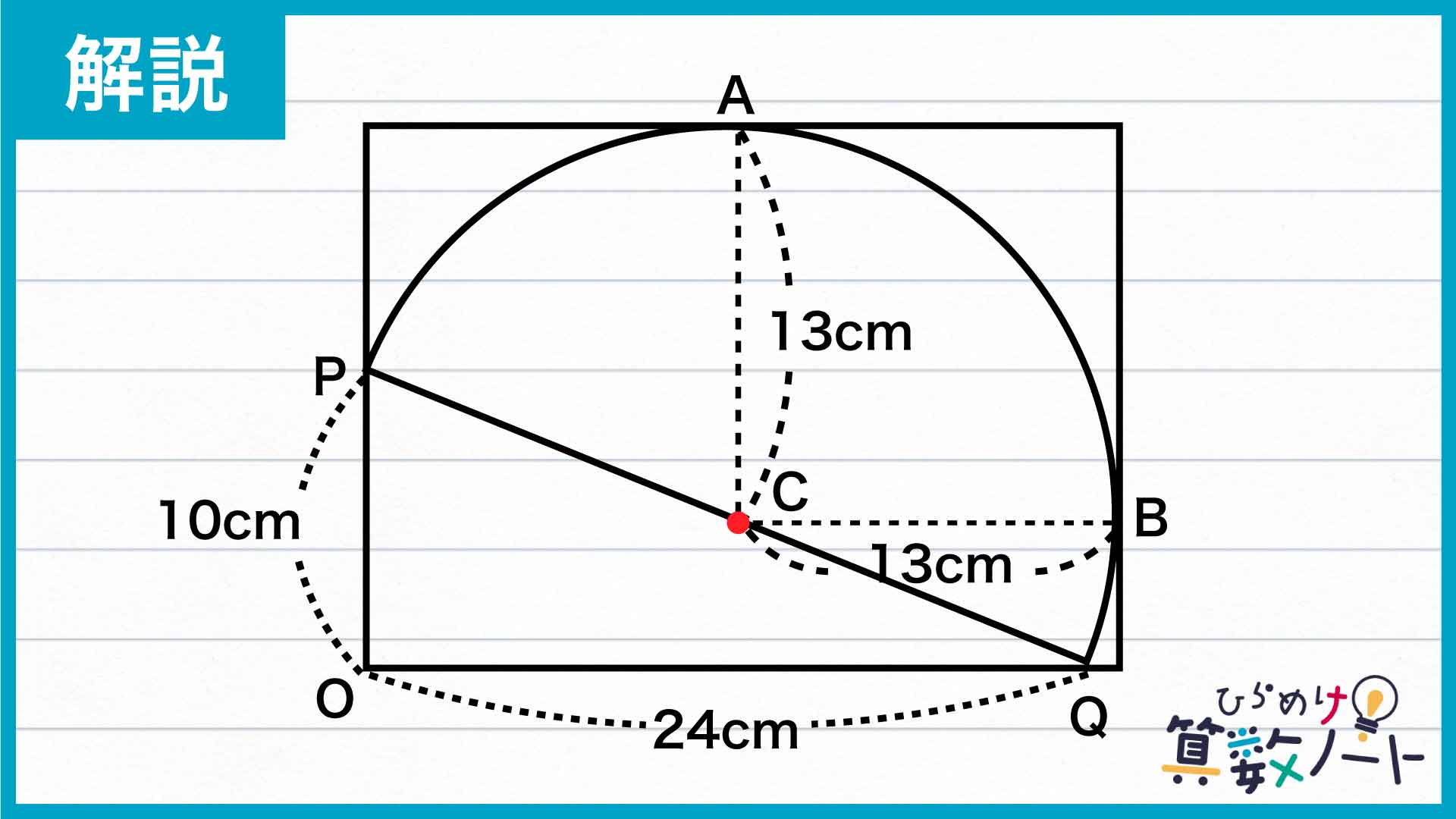
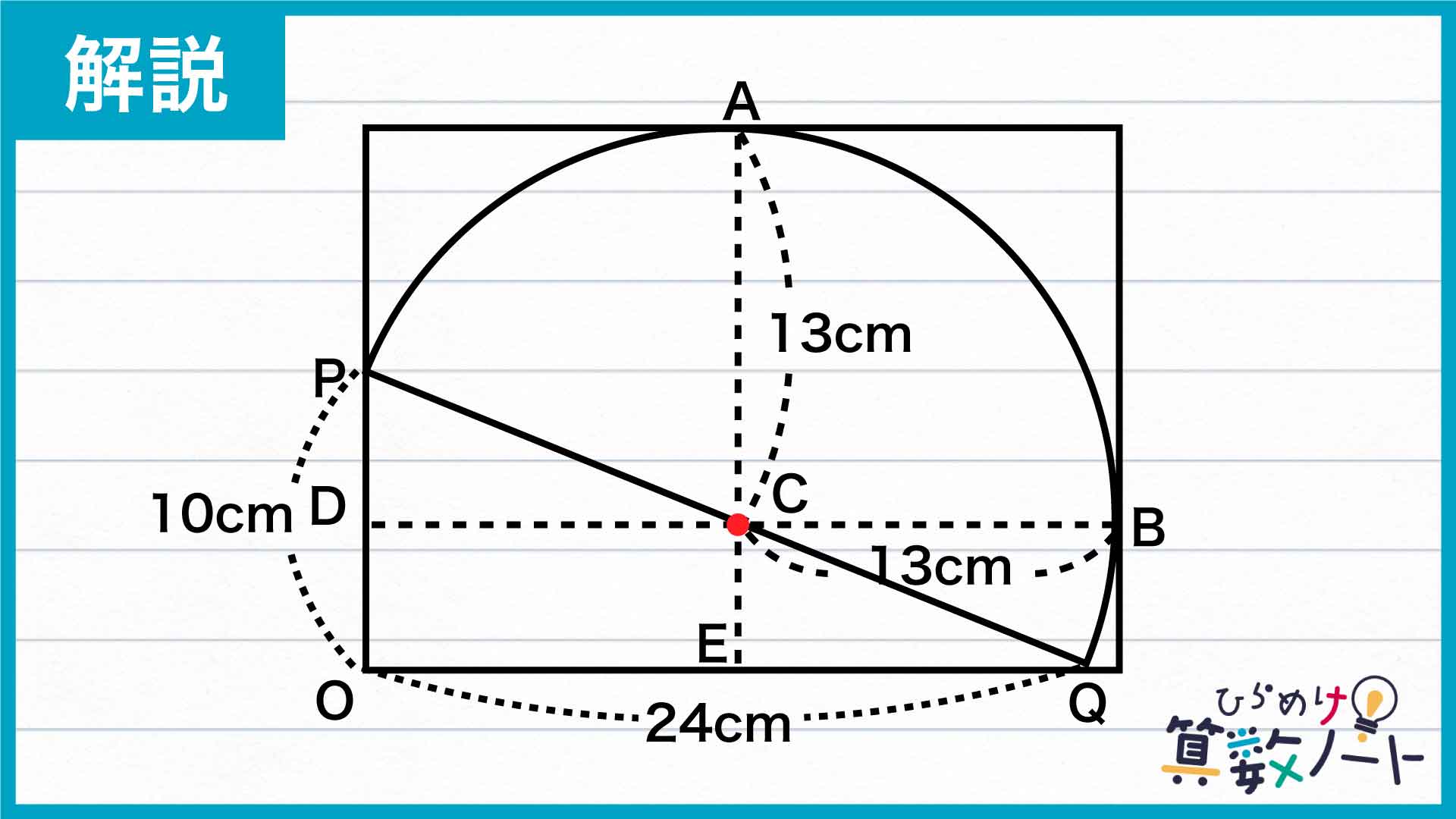
PQの中点、すなわち半円の中心をCとします。下の図のように、Cから長方形の各辺と平行となる線を引きます。

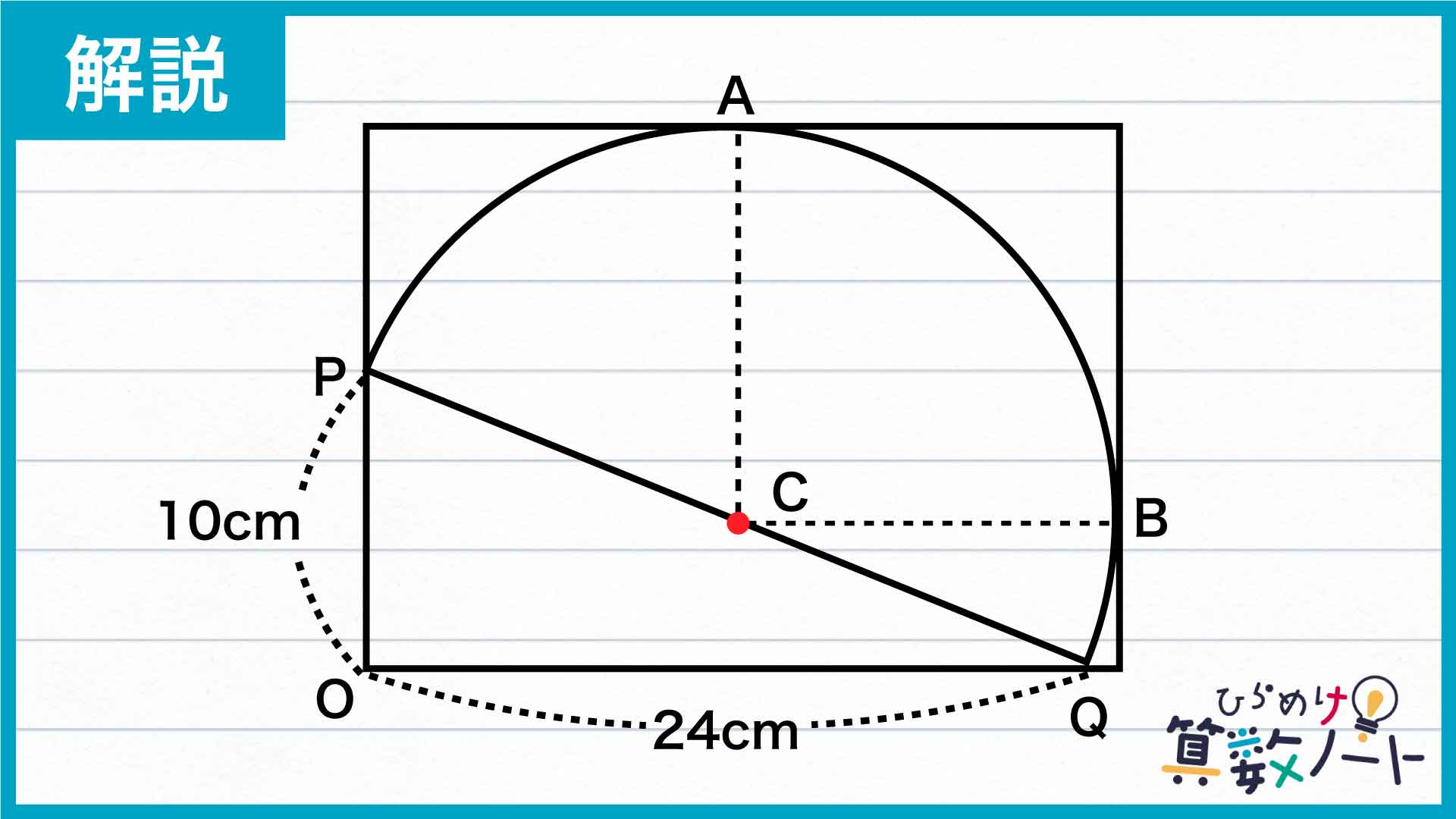
すると、Cから引いた線と長方形の各辺の交点はそれぞれ、半円と長方形の接点と一致します。

分割した長方形の辺の長さを求める

まず、CAとCBは半円の半径と等しいため、CA=CB=13cmです。

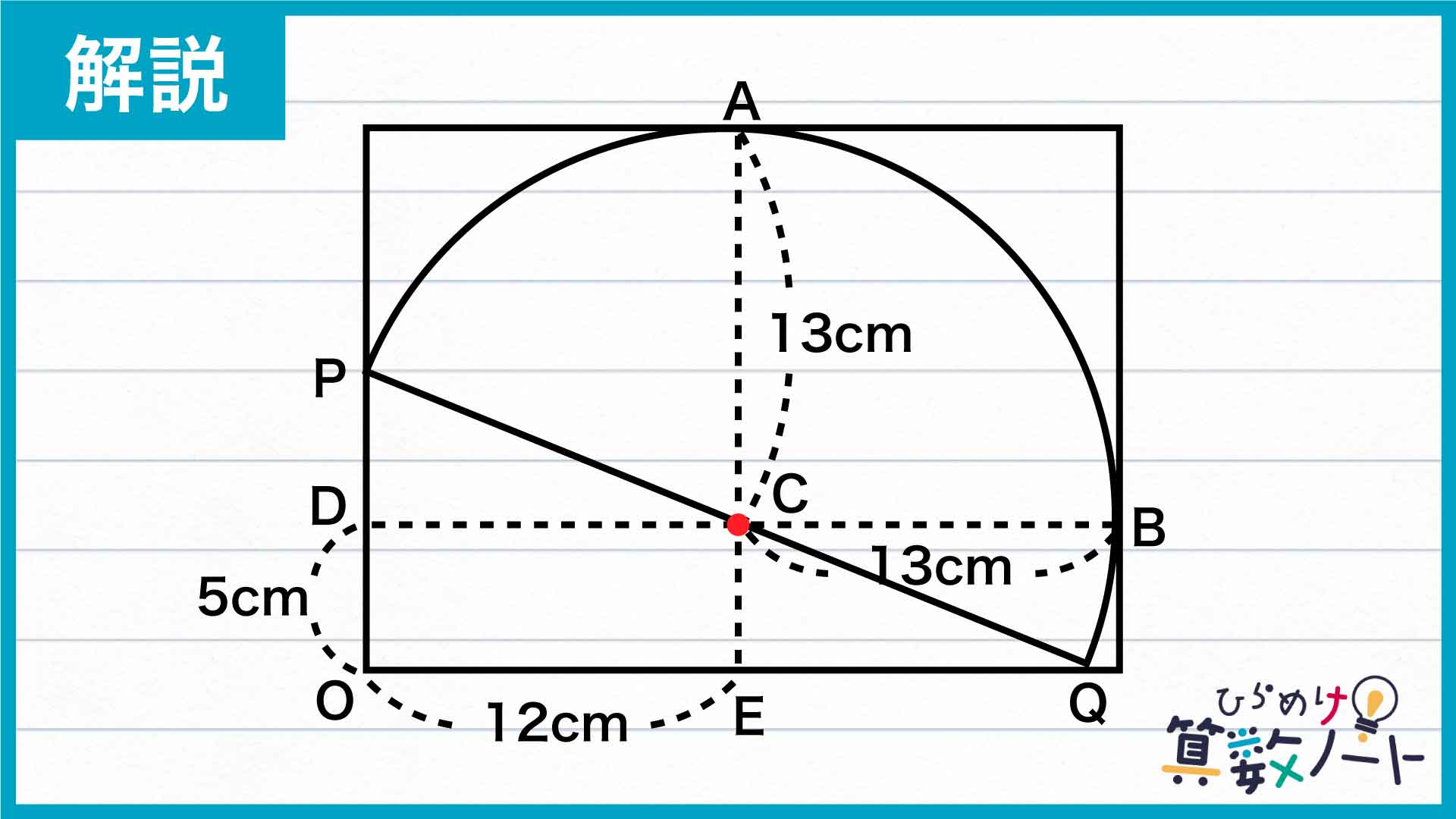
次に、三角形OPQの斜辺の中点であるCから、辺OPとOQに垂直に線を引いて交わる点をそれぞれD、Eとします。

PQはPCの2倍の長さなので、三角形OPQは三角形DPCまたは三角形ECQを2倍に拡大した図であることがわかります。

したがって、DとEはOPとOQをそれそれ二等分する点であるので、OD=5cm、OE=12cmとなります。

長方形の面積を求める

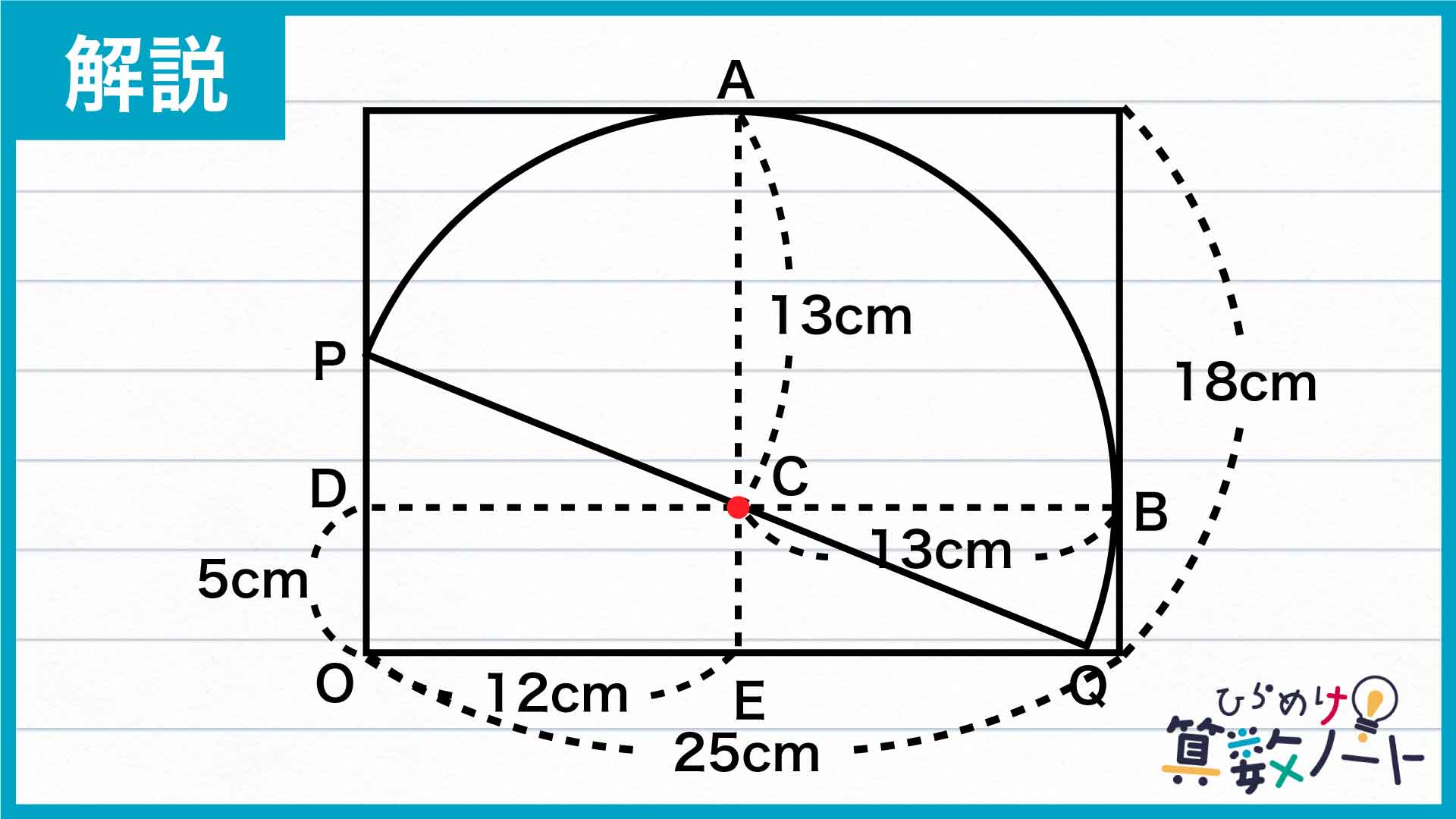
以上より、大きな長方形の縦と横の長さは、それぞれ以下のようになります。

縦の長さ：ODの長さ+CAの長さ=5+13=18cm

横の長さ：OEの長さ+CBの長さ=12+13=25cm

したがって、長方形の面積は18×25=450cm²となります。

答え：450cm²

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】