解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
次ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
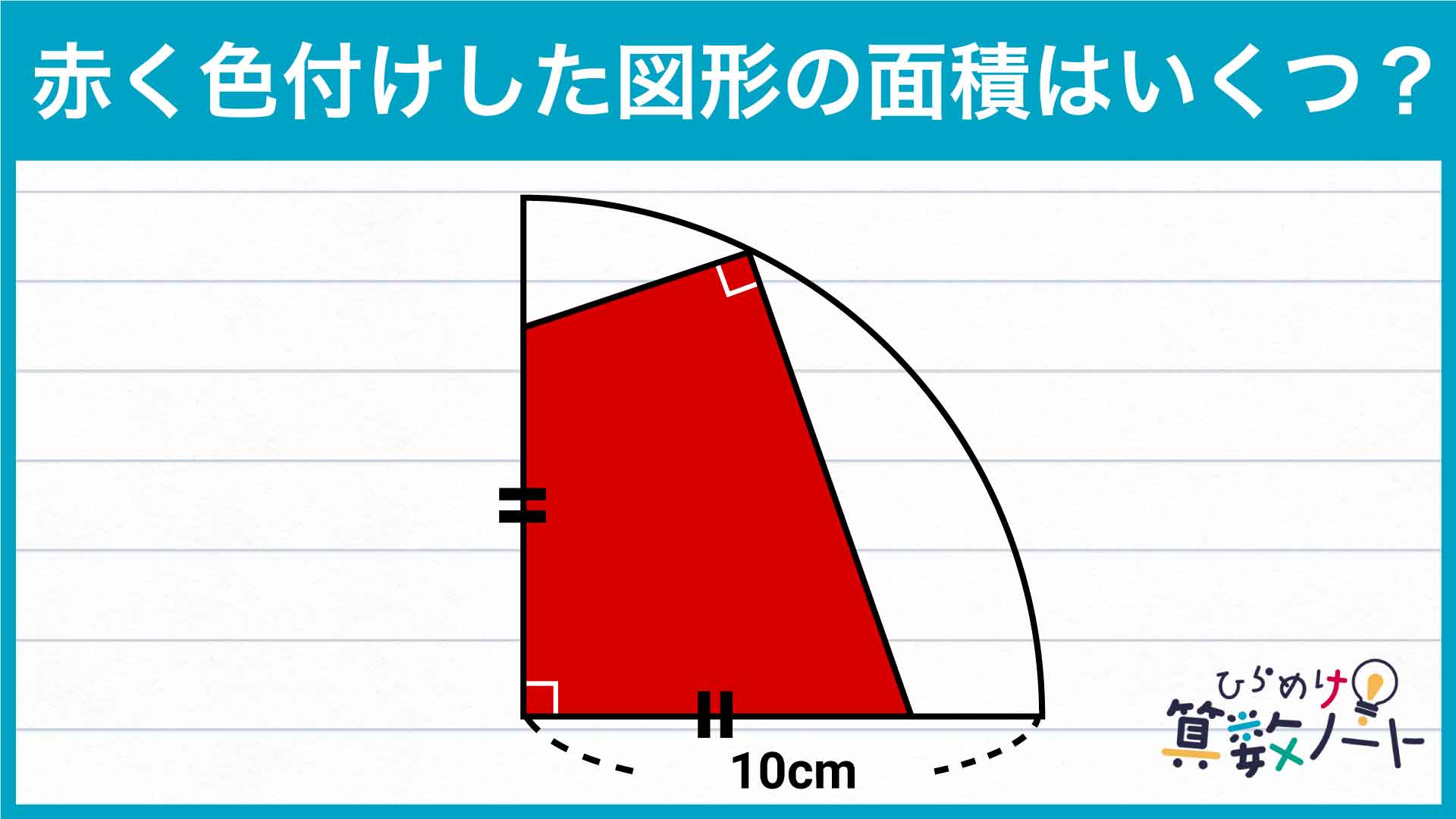
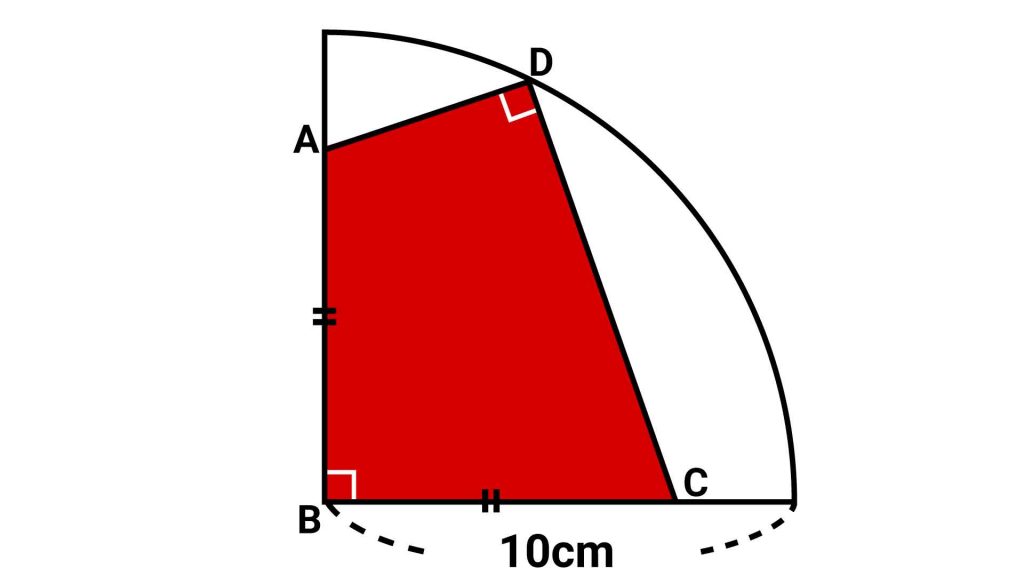
面積を求めたい四角形の辺の長さが4辺ともわかっていないので、そのままの形で求めるのは難しそうです。
そこでポイントになるのが、対角線BDです。BDは扇形の半径であり、その長さは10cmとわかっています。この長さを活かせるように、四角形を変形します。
このポイントを頭に入れた上で、問題を解いていきましょう!
図を2つに分解する
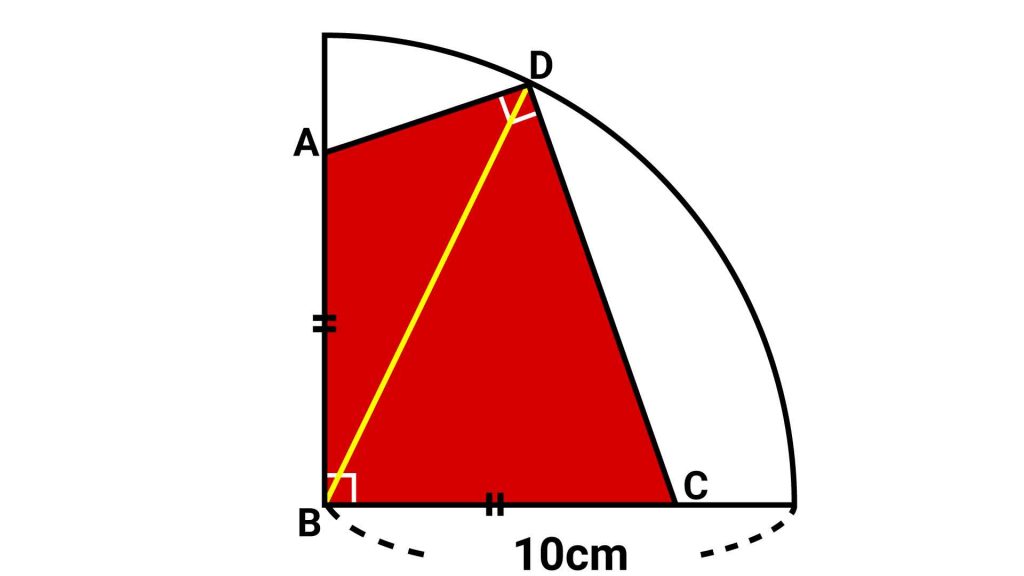
まずは、以下の図のようにBとDを結ぶ補助線を引いて、四角形を2つの三角形に分けます。
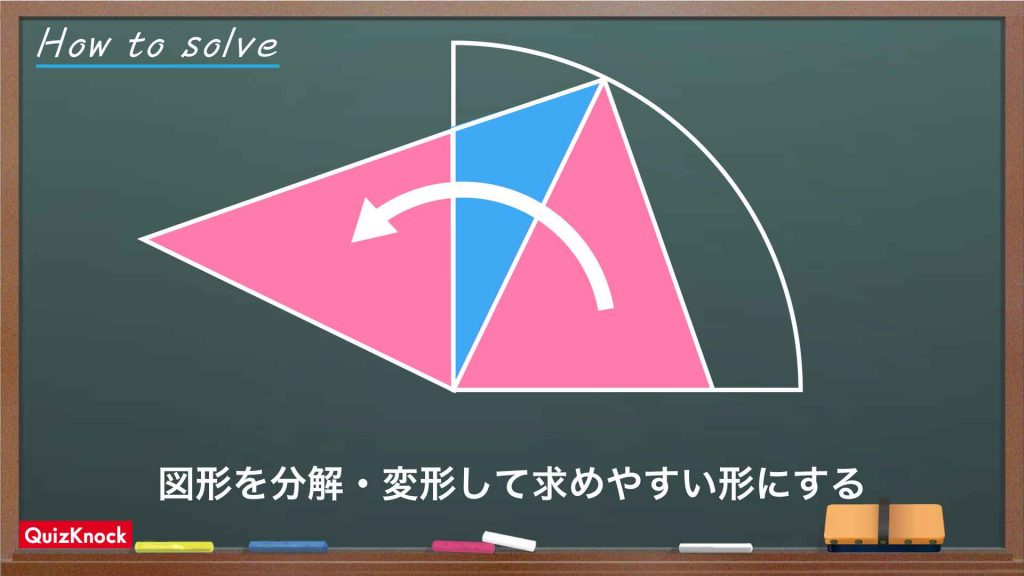
図を移動する
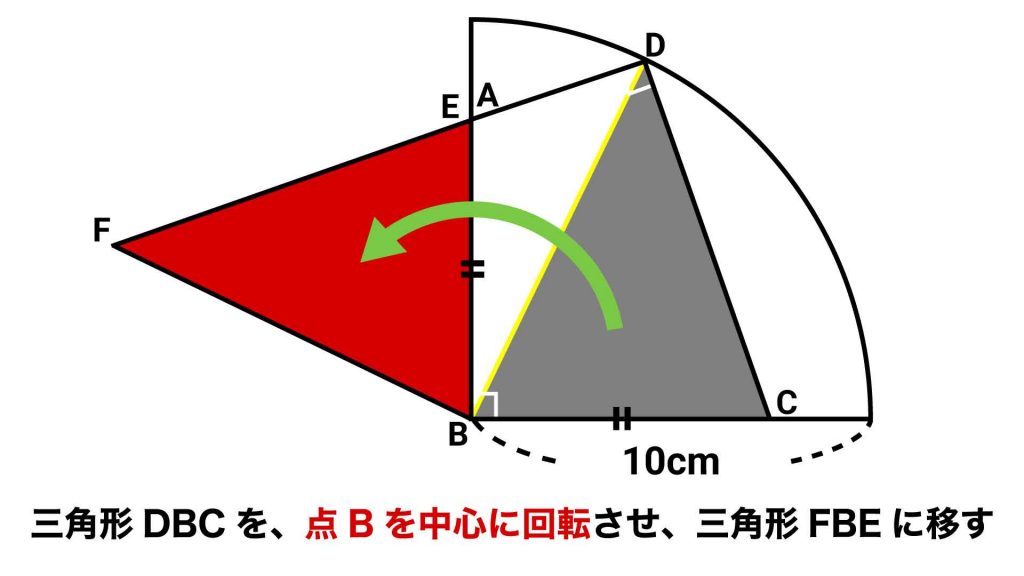
次に、補助線を引くことでできた三角形DBCを、以下の図のように移動させてみます。
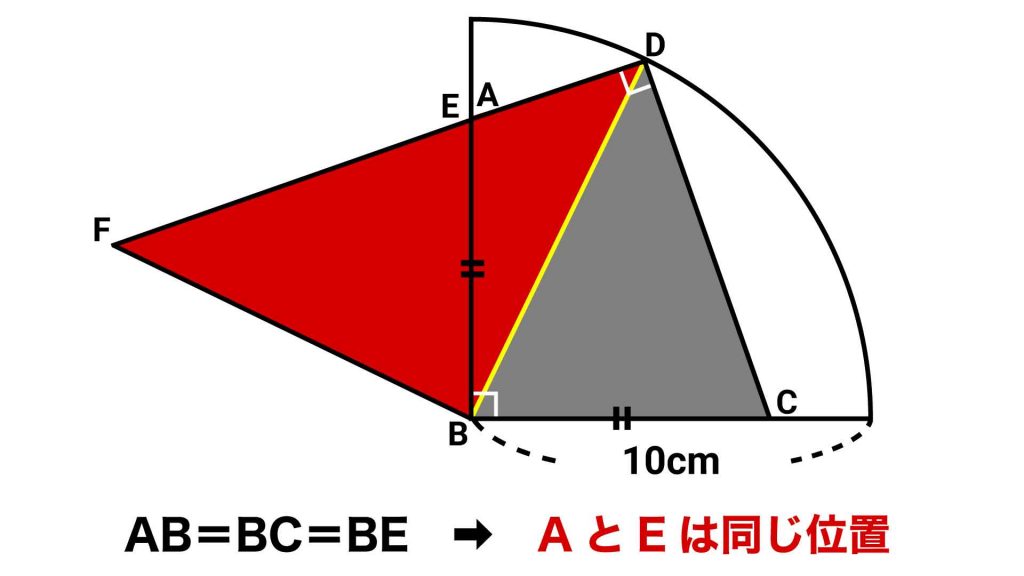
三角形DBCを移動させた後、頂点C、Dが移る点をそれぞれE、Fとすると、問題文よりAB=BC=BEなので、EはAにぴったりとくっつくことがわかります。
図形DBFは三角形?
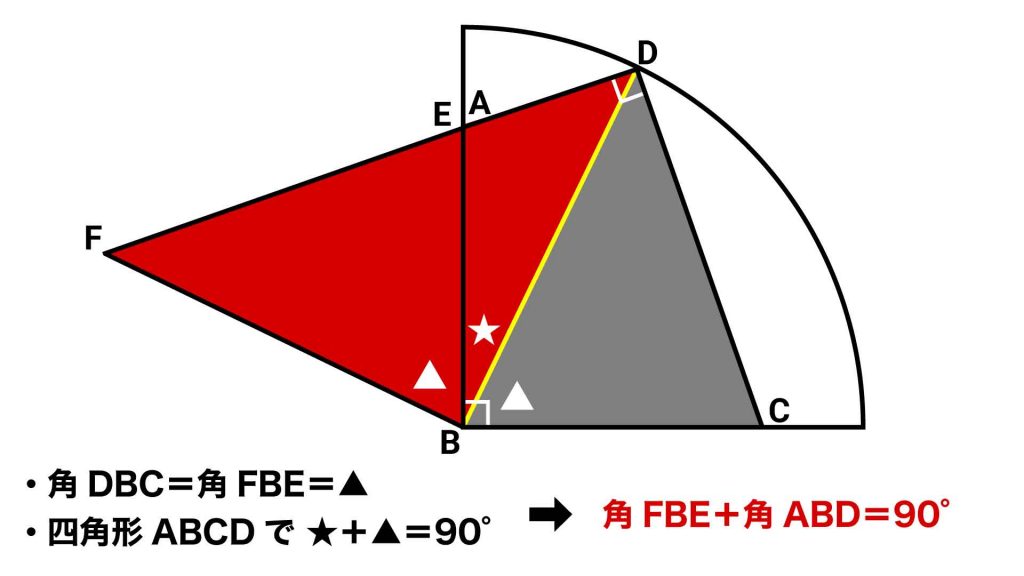
ここで、図形DBFが三角形であるかどうかを明らかにするため、辺ADと辺FEが一直線になっているかどうかを調べます。
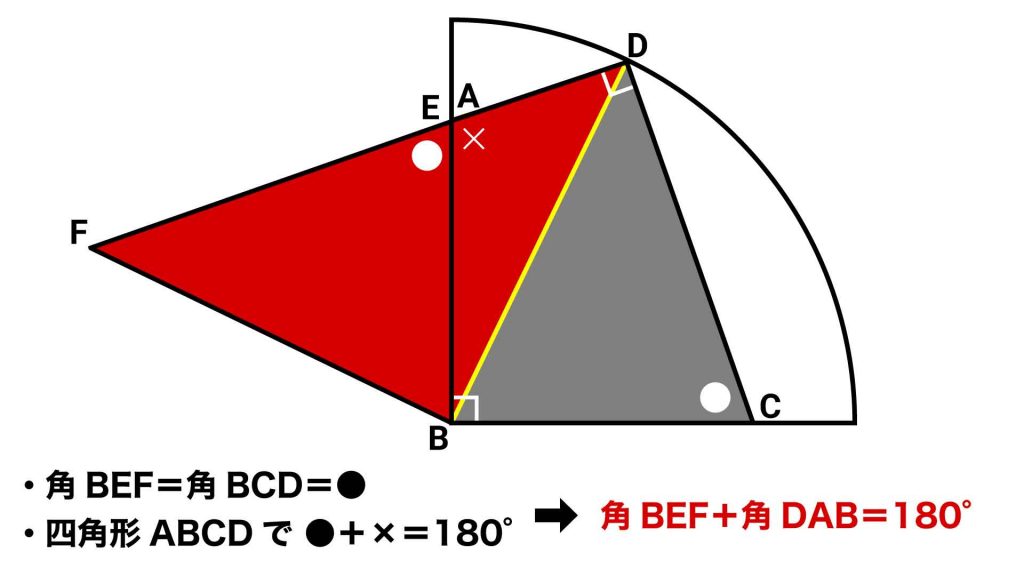
直線になっているためには、角DABと角BEFの大きさの和が180°にならなければいけません。
三角形DBCと三角形FBEは同じ三角形であり、角BEF=角BCDなので、角DABと角BCDの角度の和が180°であれば、辺ADと辺FEが一直線になっているといえます。
角DABと角BCDは、四角形ABCDの角のうち、直角でない2つの角です。したがって、角DABと角BCDの角度の和は、360-(90+90)=180°となります。
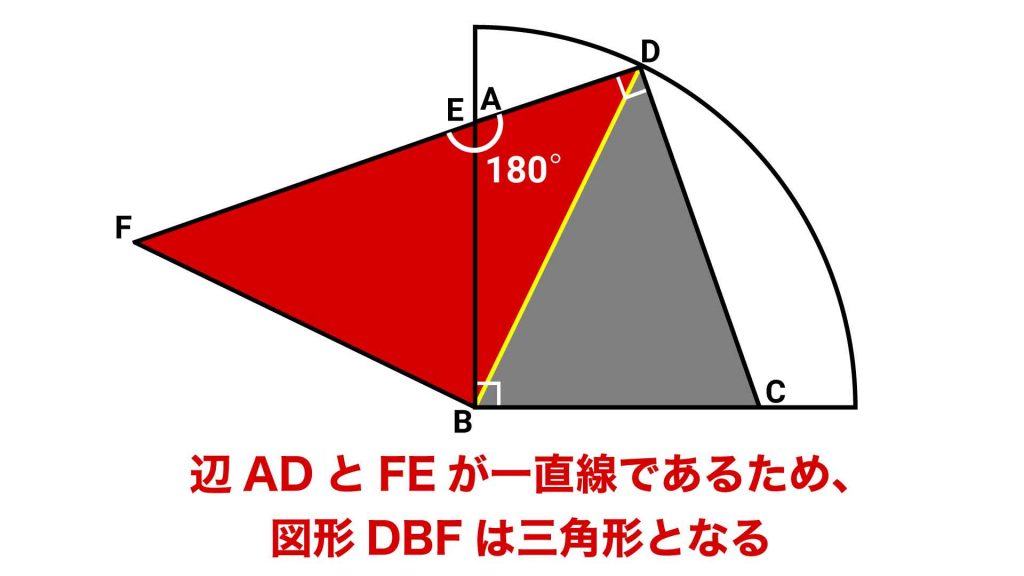
角DABと角BEFの和が180°でしたので、辺ADと辺FEが一直線になっていることがわかりました。辺ADと辺FEが一直線になっているため、変形した後の図形はB、D、Fが頂点の三角形になります。
角DBFの大きさを求める
次に、角DBFの大きさを求めます。
角DBFは、角ABDと角FBEの和で求められます。角FBEは先ほどの三角形の移動によってできた角なので、角FBE=角DBCです。
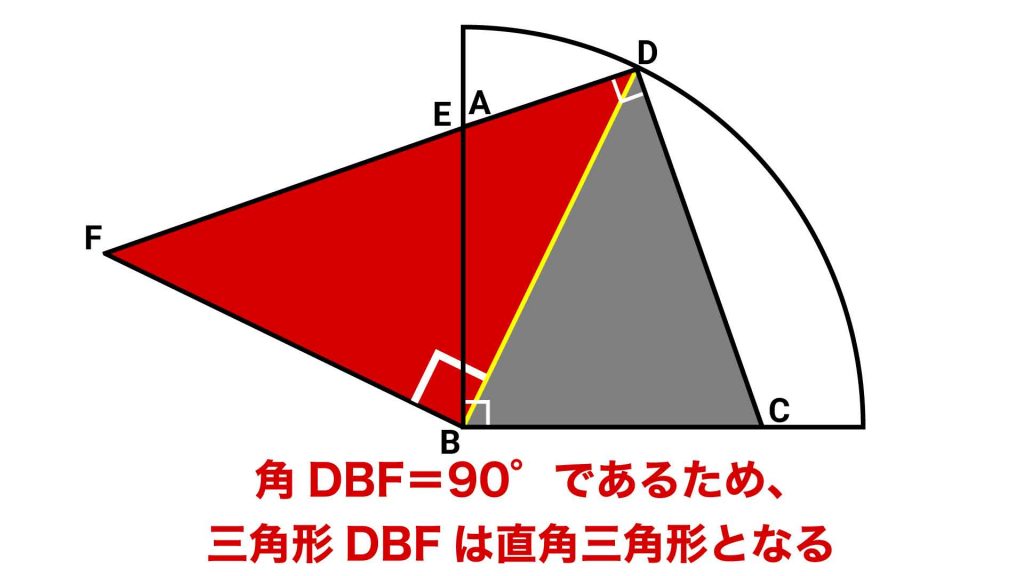
また、角ABD+角DBC=角ABCであり、角ABCの大きさは、四角形ABCDのひとつの直角であるため90°です。したがって、角DBFも90°であるとわかります。
以上より、三角形DBFは、角DBFが90度の直角三角形となります。
三角形DBFの面積を求める
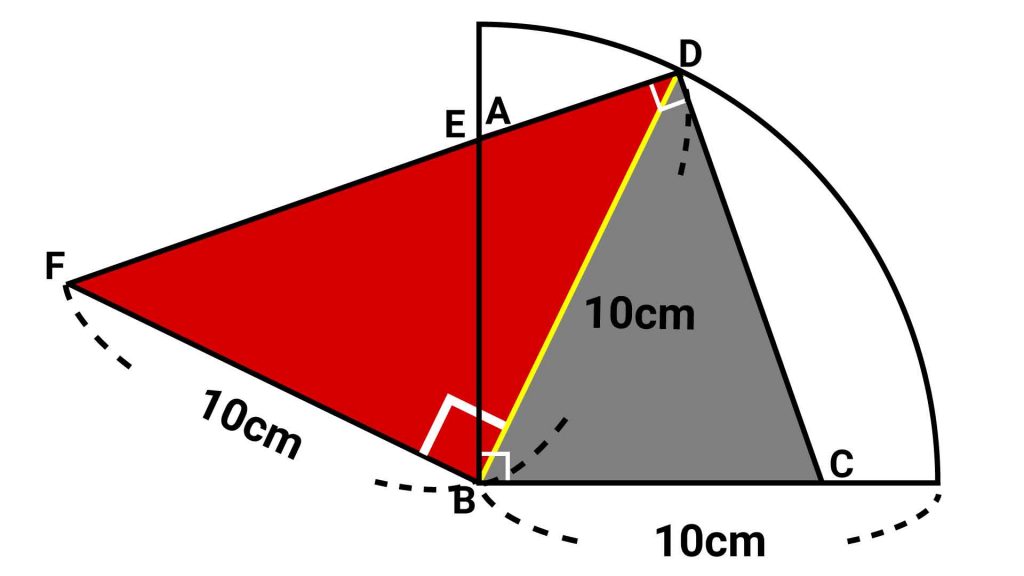
直角三角形DBFの面積は、辺DB×辺BF÷2で求めることができます。
辺DBの長さはおうぎ形の半径の長さと等しいので10cmです。また、辺BFは三角形BCDの移動によってできたものなので、こちらの長さも辺DBと同じく10cmとなります。
したがって、直角三角形DBFの面積は10×10÷2=50cm2となるため、もとの四角形ABCDの面積も50cm2となります。
答え:50cm2
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】











.jpg)









.jpg)







