解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
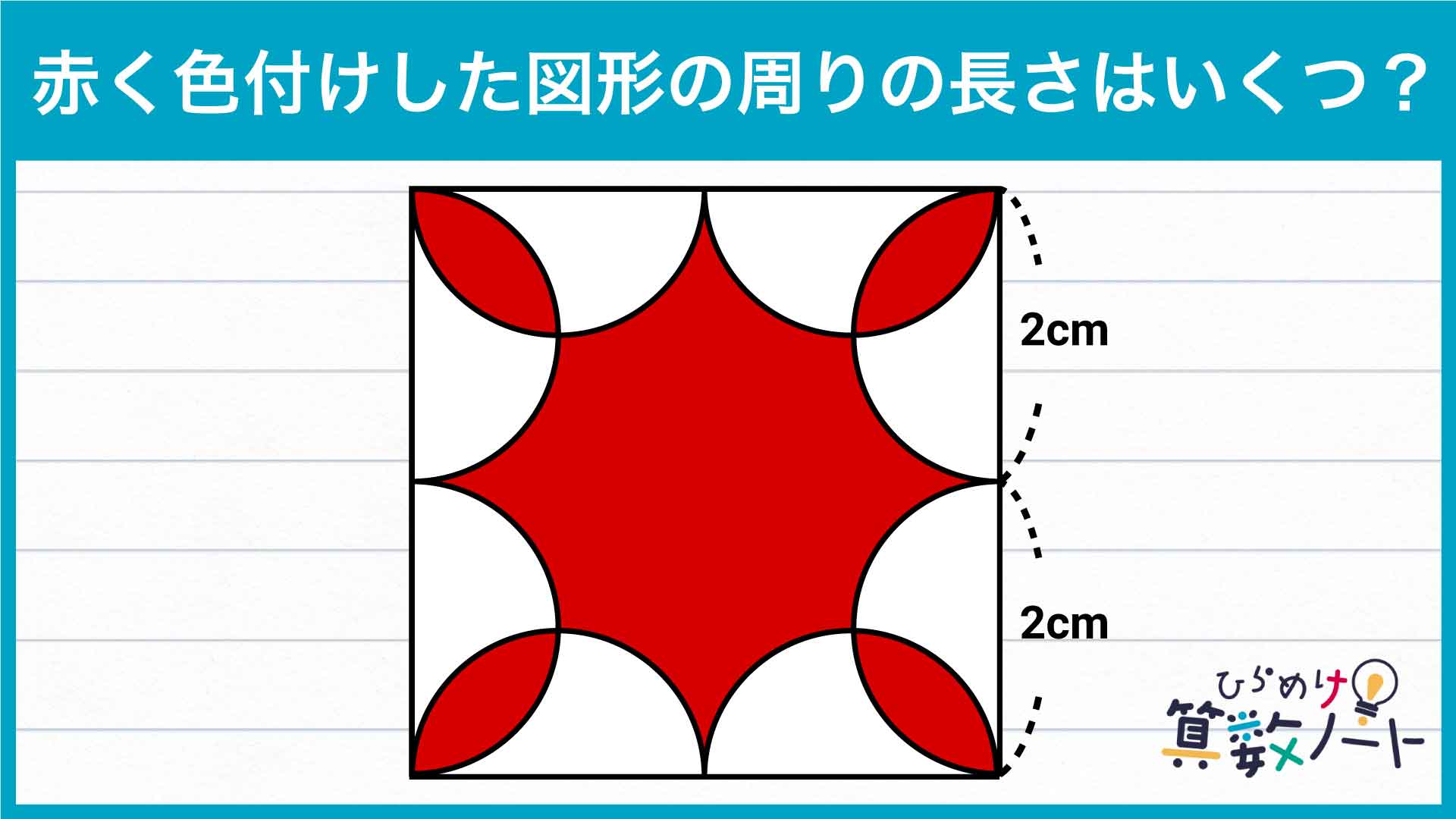
今回のポイントは、「図形の周りを分解する」ことです。
求める図形がどのような要素から成り立っているのかを考えると、意外と簡単に答えにたどり着くことができます。
以上を踏まえ、問題を解いていきましょう!
一部分の長さを求めてみる
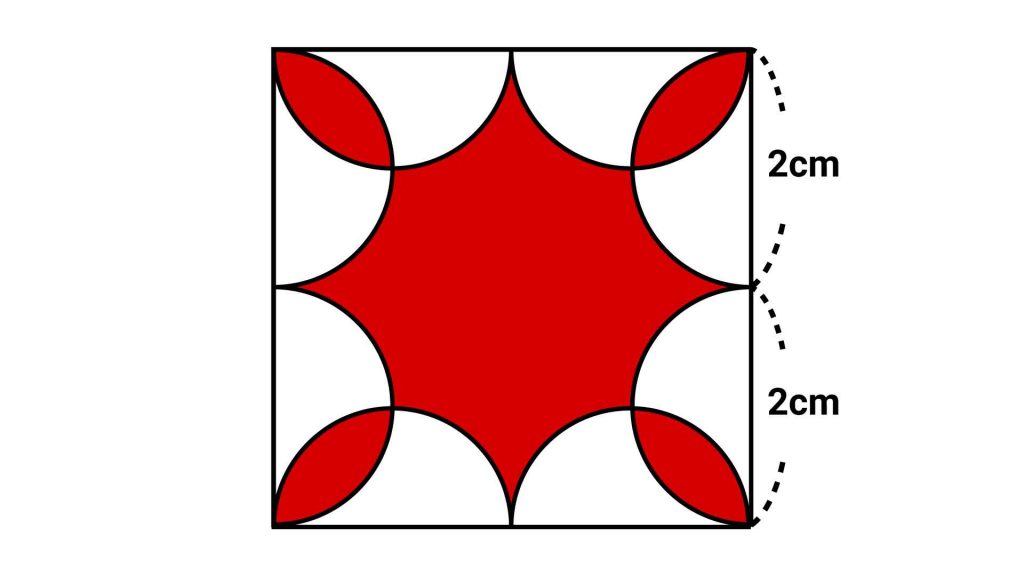
求める図形の構成要素を見極めるにあたって、まずは「どの部分の長さを求めることができるか」のあたりをつけます。
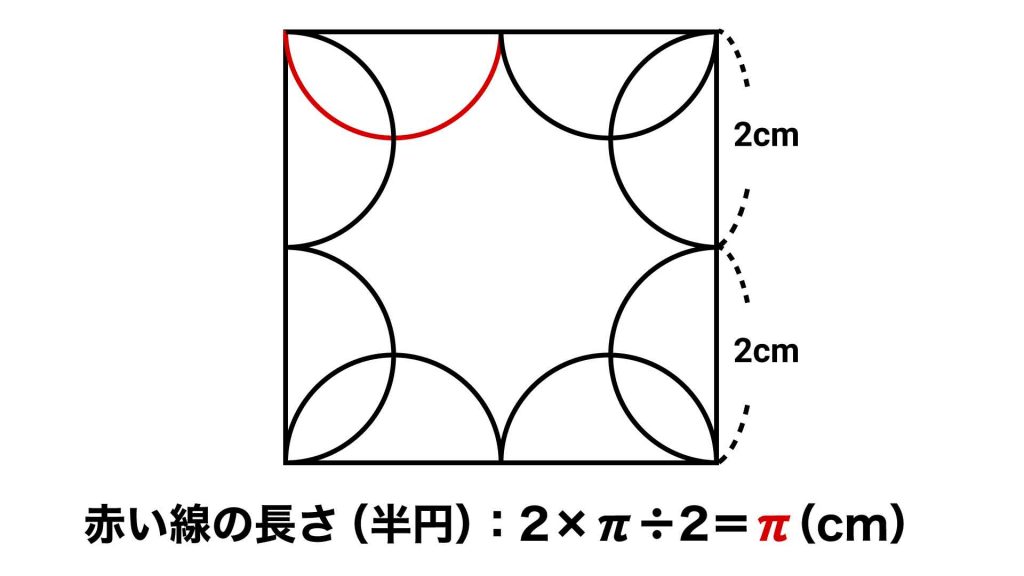
すると、下図で示した部分が簡単に求まりますね。
図の赤い線は直径2cmの半円の弧なので、その長さは2×π÷2=πcmとなります。
全体の長さを求める
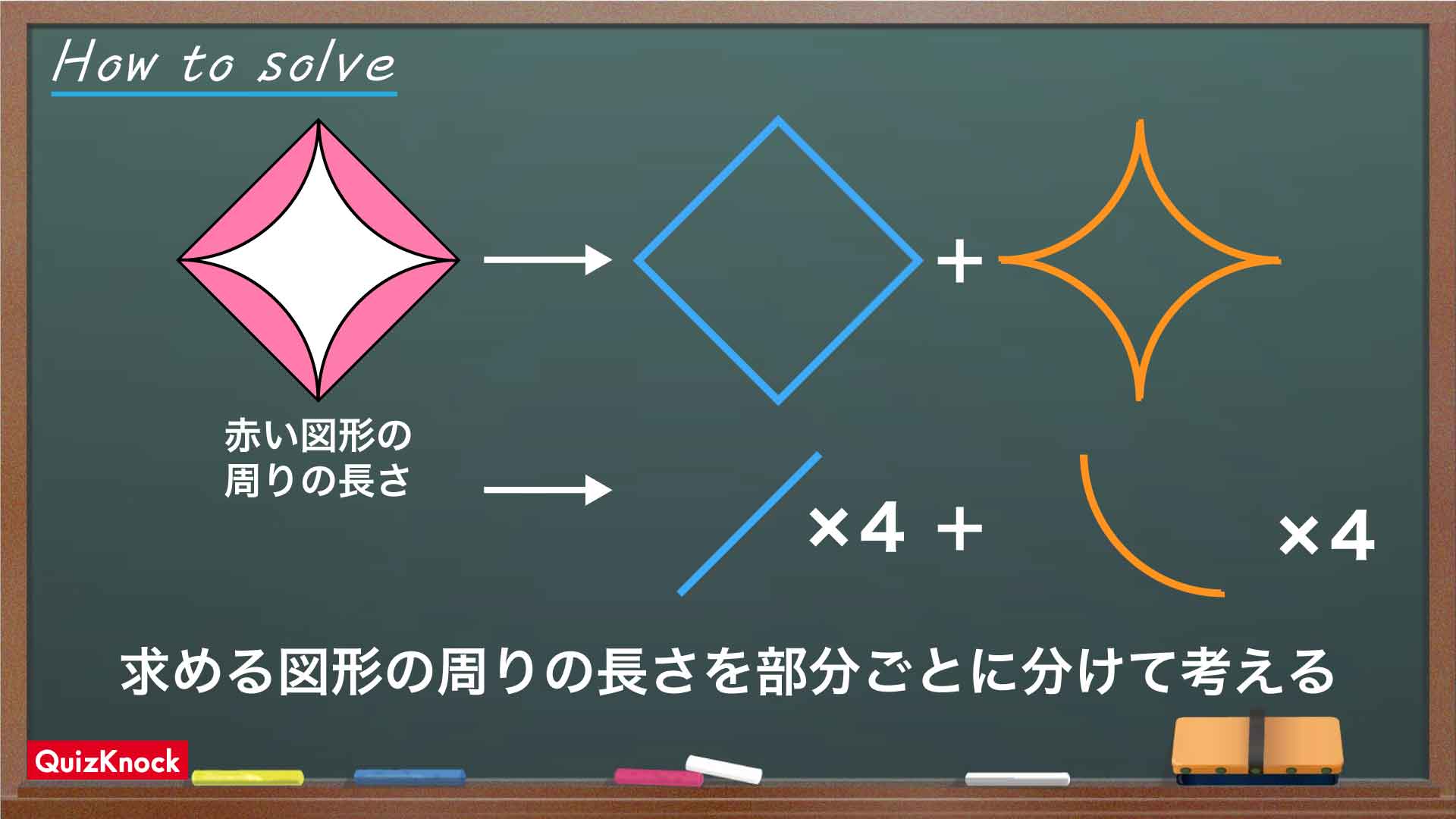
図形の周りにある半円の存在がわかれば、その半円が1つだけではないことに気づくかと思います。そうやって1つ1つ見ていくと、求める図形の周囲が全て半円の弧で構成されているということがわかります。
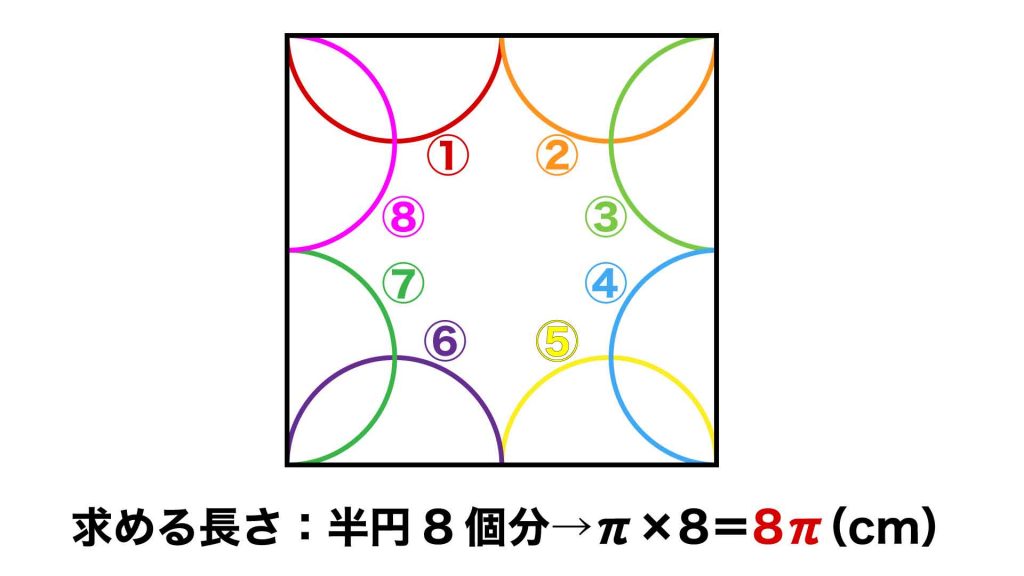
以下のように周囲の線を色分けしてみると分かりやすいですね。
以上より、求める図形の周りの長さは、直径2cmの半円の弧8つ分であることがわかりました。
よって、答えはπ×8=8πcm2となります。
答え:8πcm
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)










.jpg)







