解説
それでは解説です。さまざまな解き方がありますが、ここではその一例を紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
今回のポイントは、「1つの記号のみで式を表す」ことです。
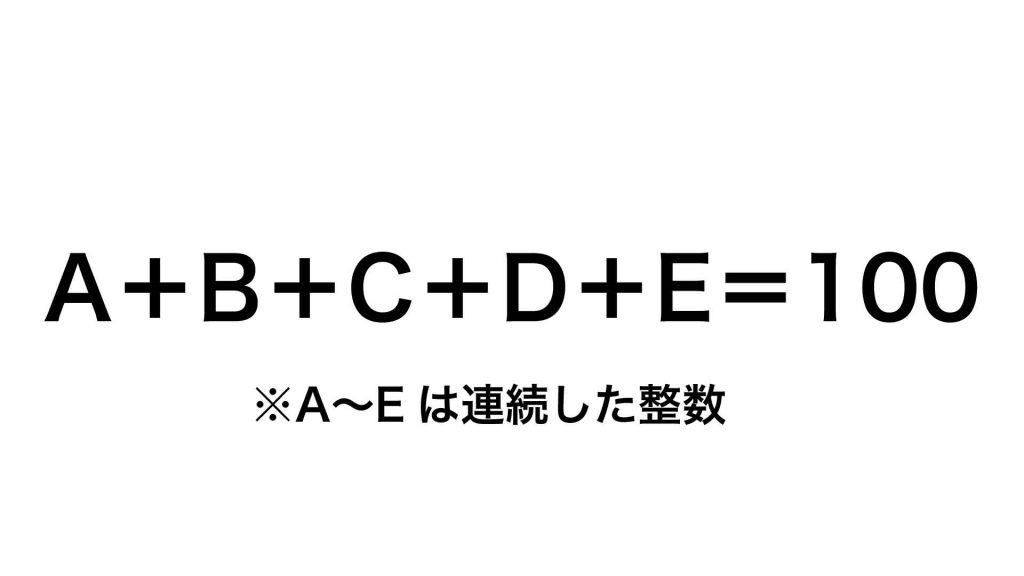
連続した整数の組がある場合、そのうちの1つを用いて他の数を表すことができます。
以上を踏まえ、問題を解いていきましょう!
全ての記号をCで表す
まずは上で示した方針に従い、AからEの記号を全てCで表します。
もとの式をCで表す
Cで表したAからEを、もとの式に当てはめると以下のようになります。
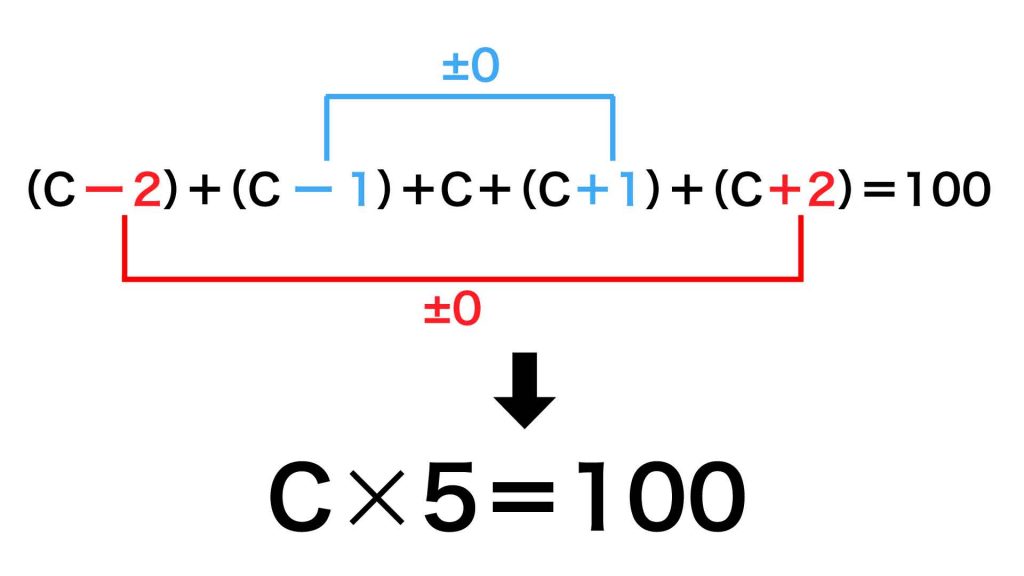
C-2とC+2、C-1とC+1がそれぞれ1組ずつあるので、足し引きするとC×5=100という式が残ります。
以上より、Cは100÷5=20と求められます。EはCより2だけ大きいので、22となります。
答え:22
それでは、次回の算数ノートでお会いしましょう。
「ひらめけ!算数ノート」のバックナンバーはこちらからどうぞ。
【前回の算数ノートはこちら】
【あわせて読みたい】











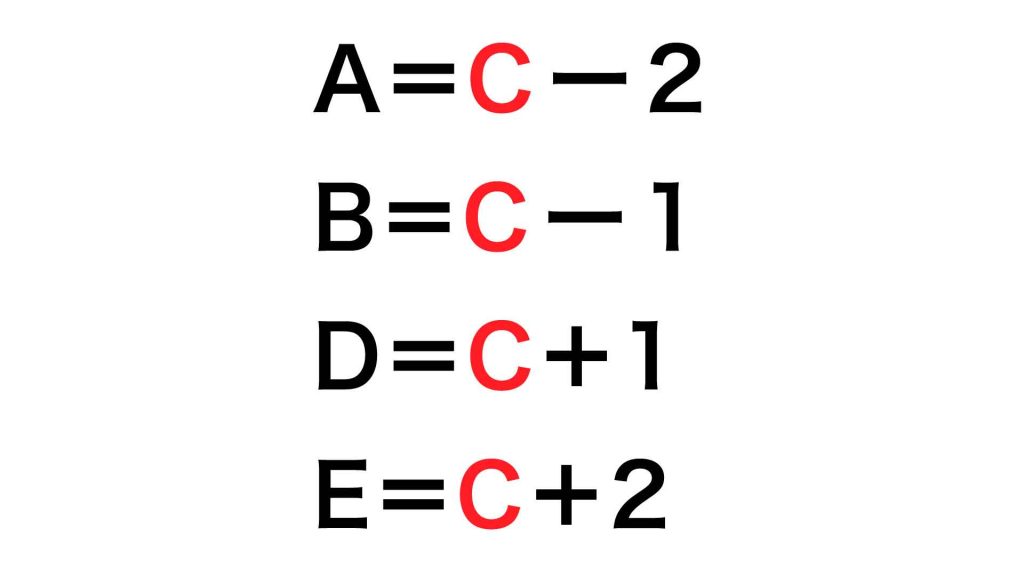
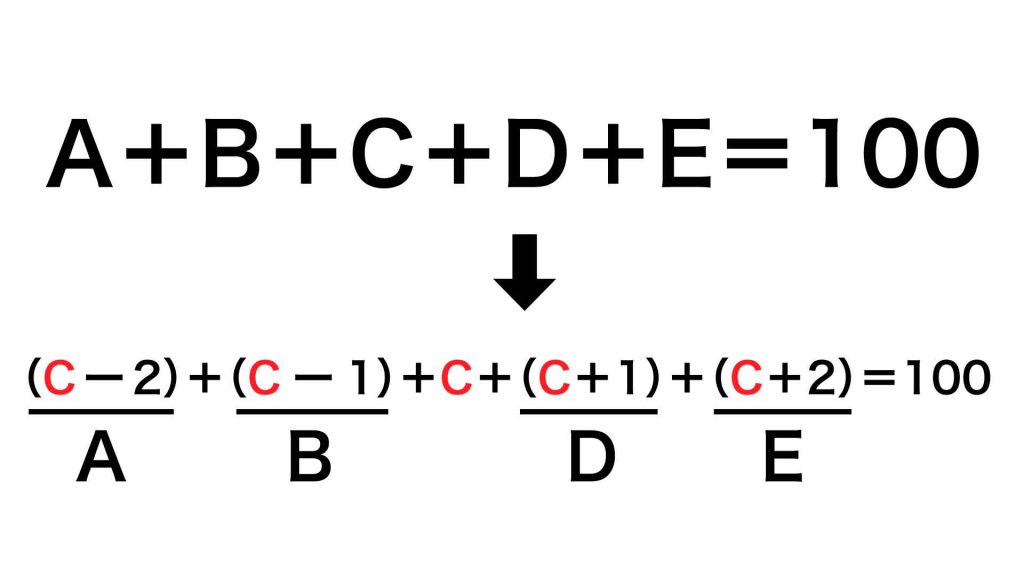
.jpg)







.jpg)






