解説
それでは解説です。さまざまな解き方がありますが、ここではその一例を紹介します。
前ページ：【解答フォーム】自力で解きたい方はこちらへ！ 以下は問題の答えです
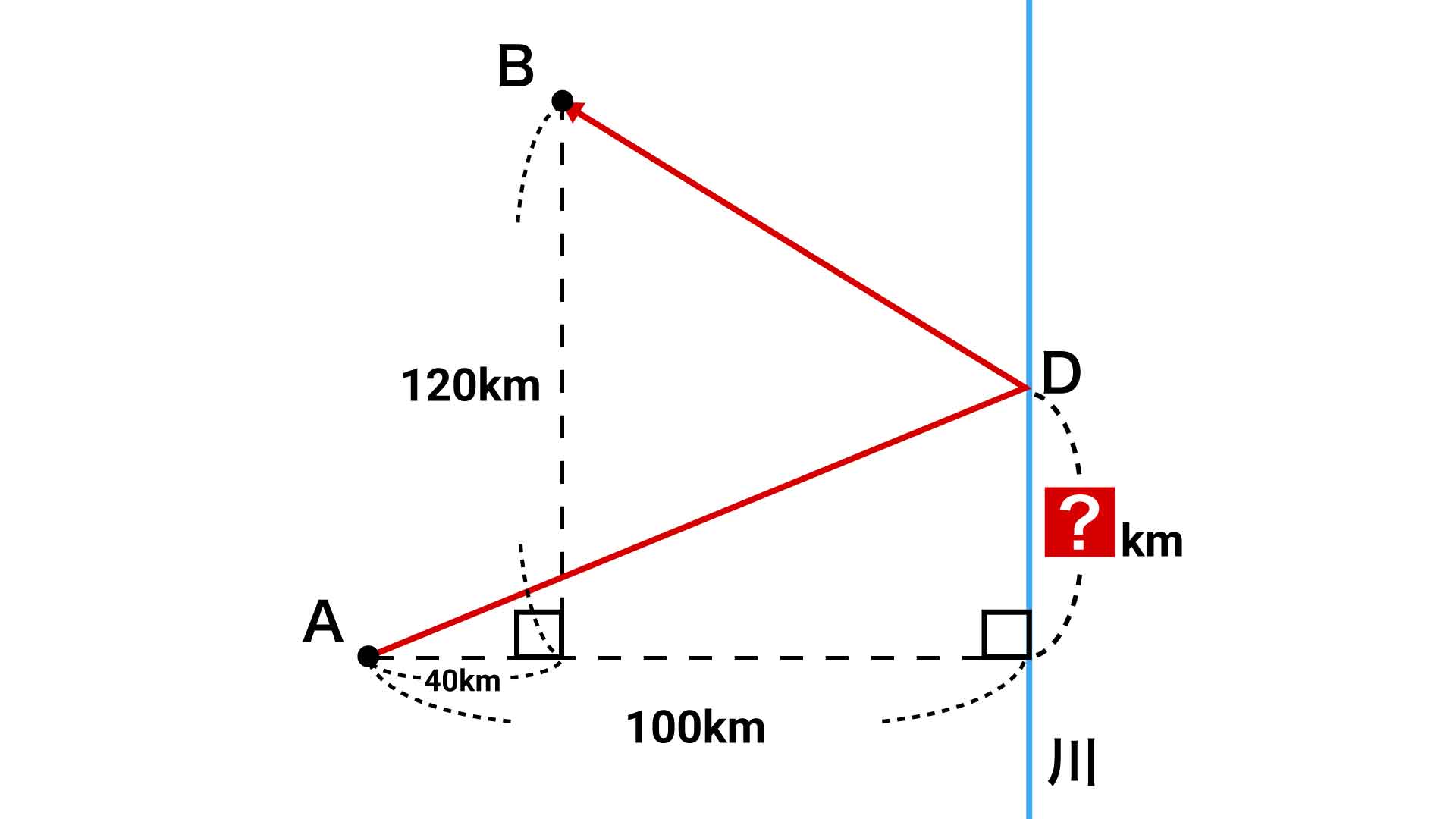
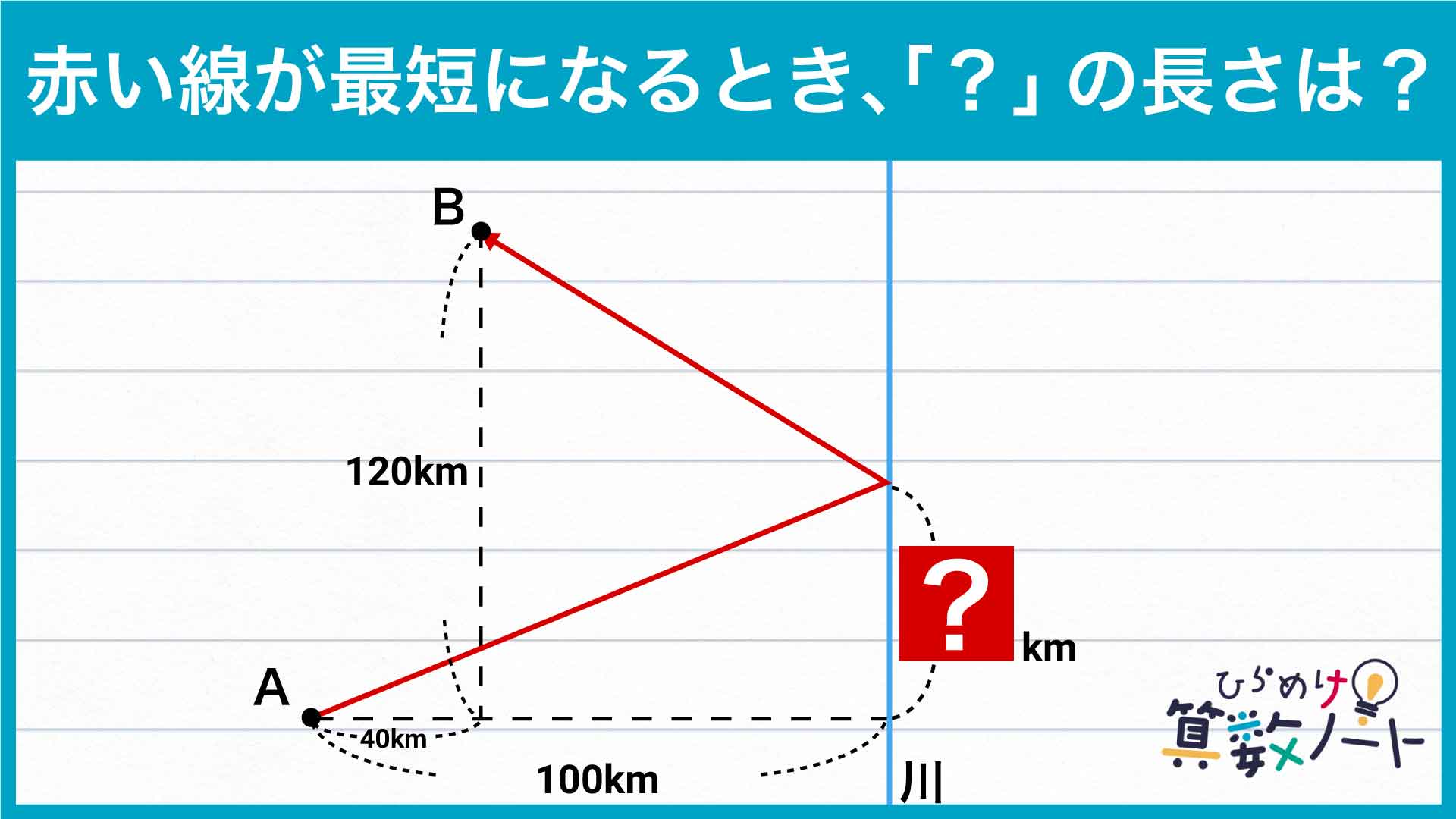
今回の問題の解き方をまとめた図がこちらです。ポイントはB地点について、川に対して対称な点を考えることです。
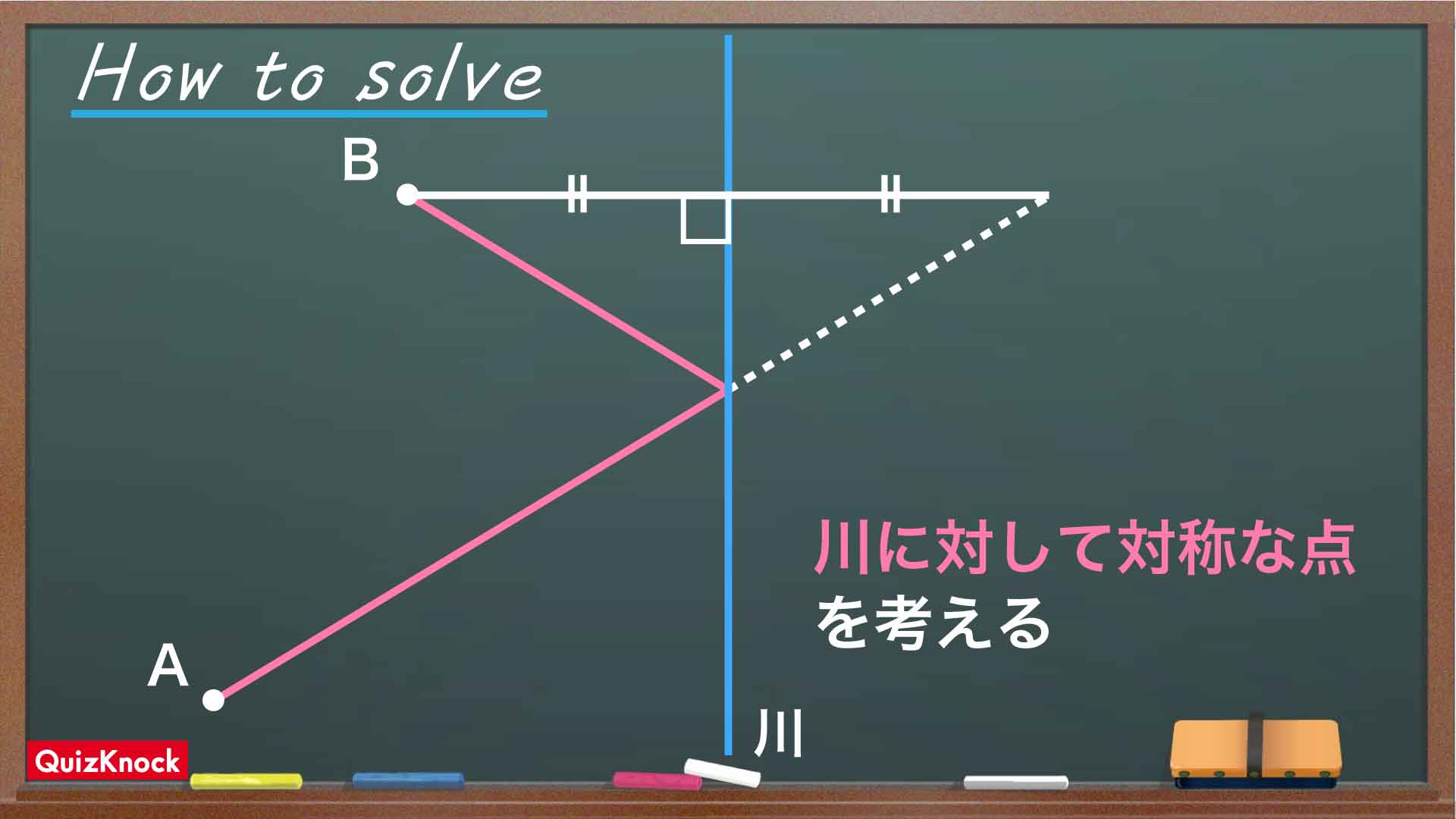
この図の流れに沿って、解いていきましょう！
川に対して対称な点は？
まず、以下の図のように、B地点について川に対して対称な点を考え、これをC地点とします。
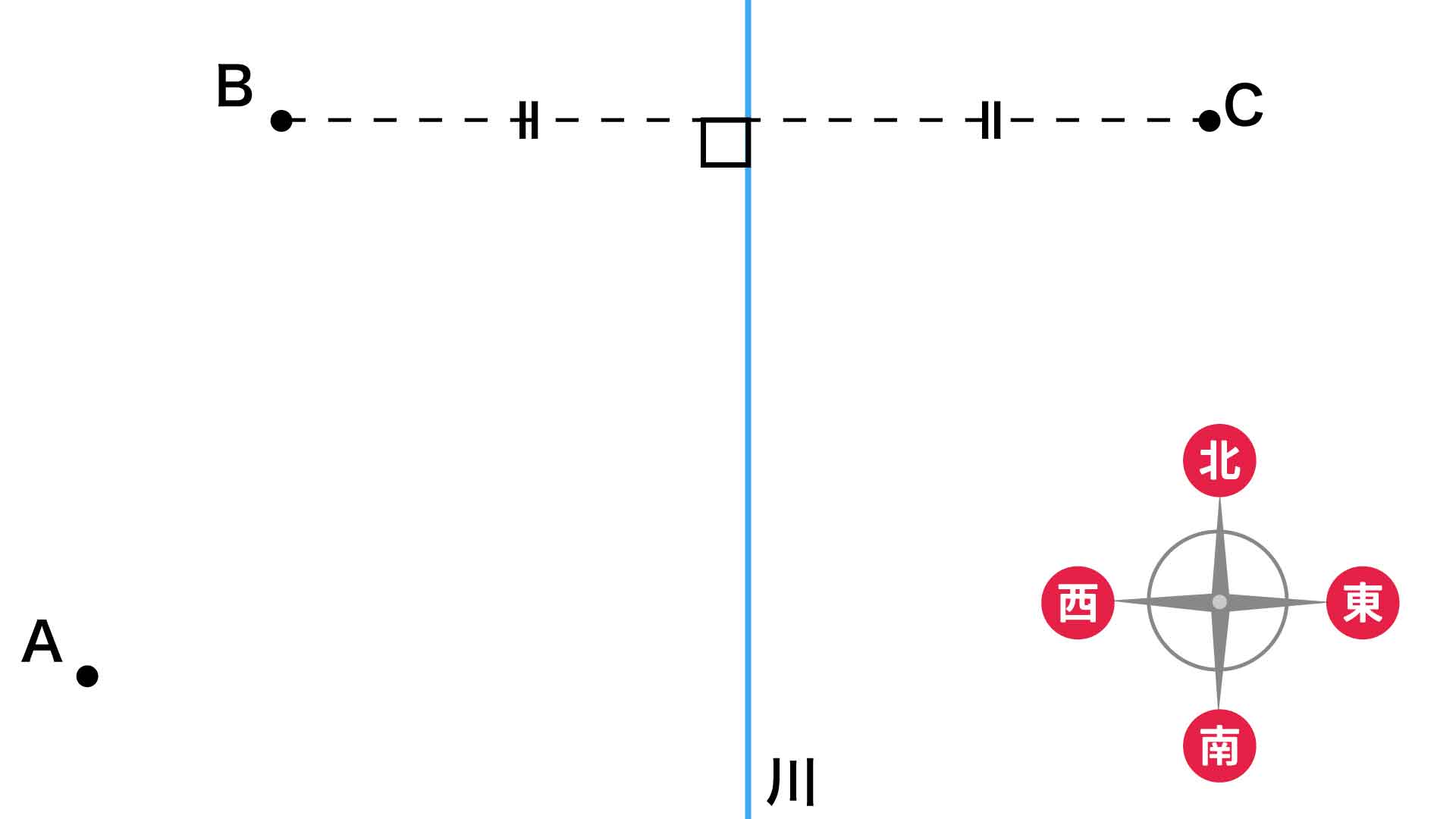
B地点はA地点から「東に40km、北に120km」の場所に、南北に流れる川は「A地点から東に100km」の場所にあります。したがって、B地点は「川から100-40=60km西」に、C地点は「川から60km東」にあり、A地点からは「東に160km、北に120km」の場所にあることがわかります。
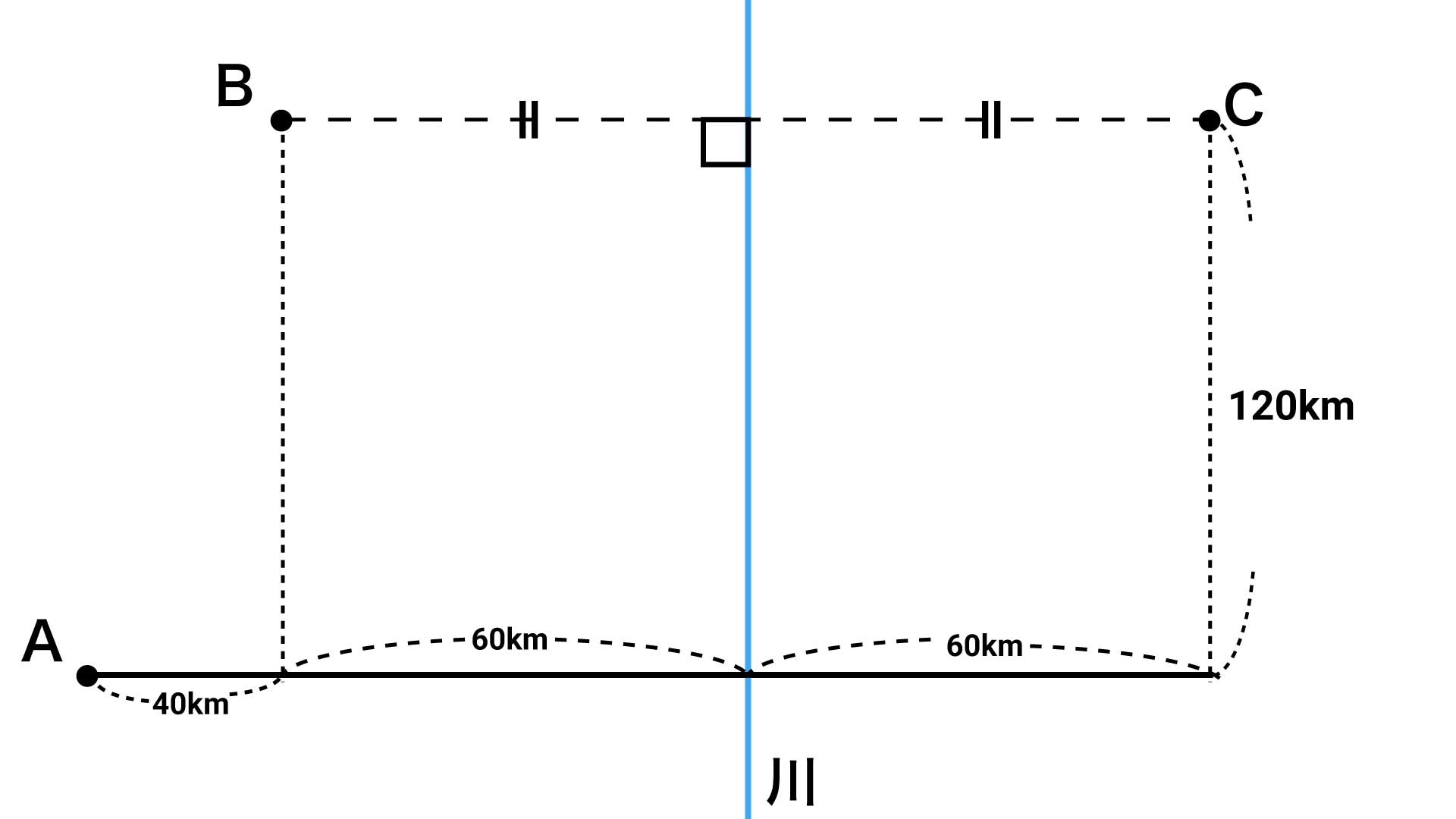▲位置関係を整理するとこんな感じ
A地点→川→B地点の移動距離は？
水を汲む地点をD地点とすると、移動距離はAD+DBと表されます。
ここで、B地点とC地点は川に対して対称であることから、DB間の長さとDC間の長さが等しいことがわかります。
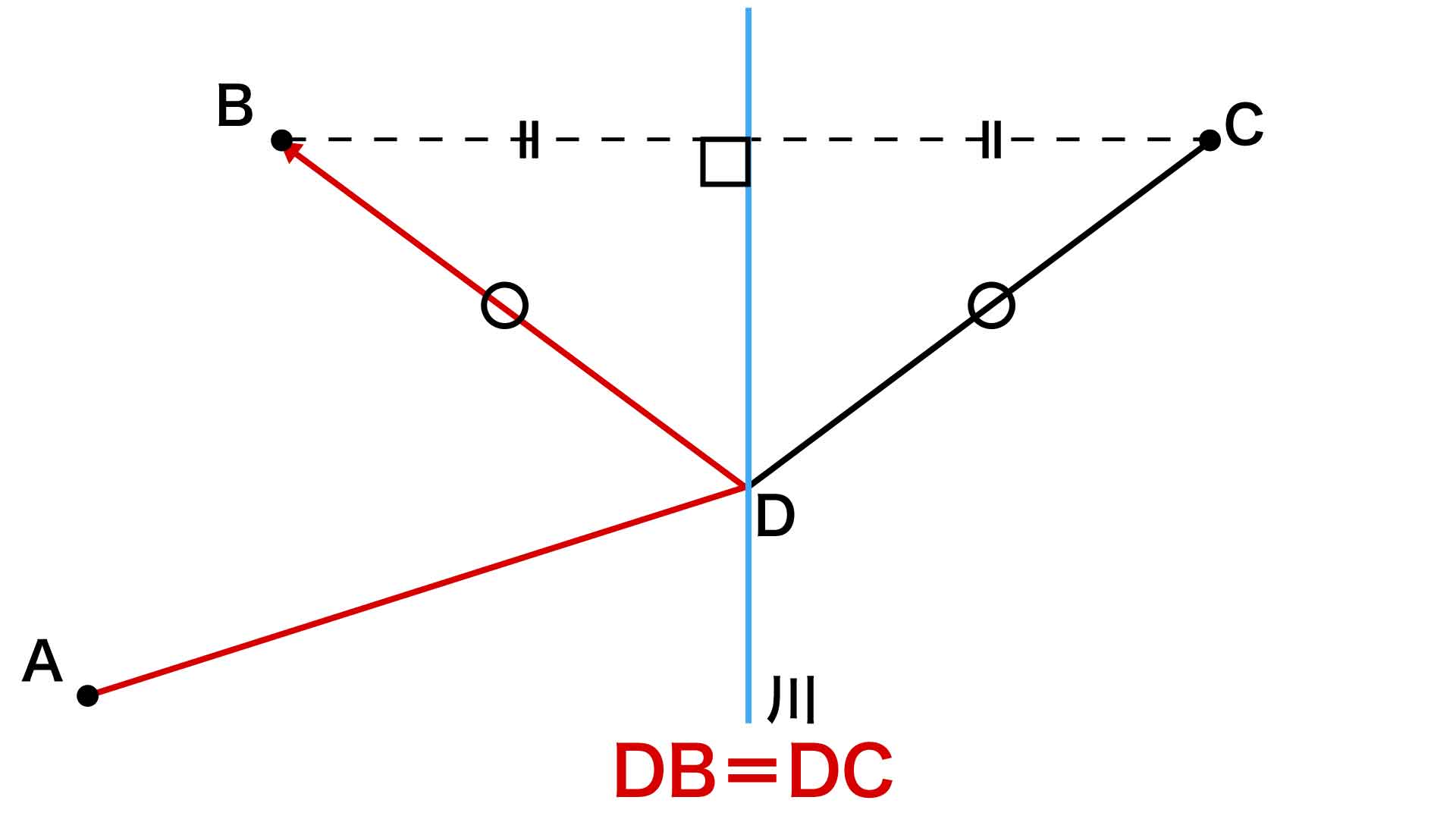
したがって、移動距離が最短になるのは、AD+DCが最小になるときです。
あと一歩！
AD+DCが最小になるのは、下図のように直線AC上にD地点があるときです。
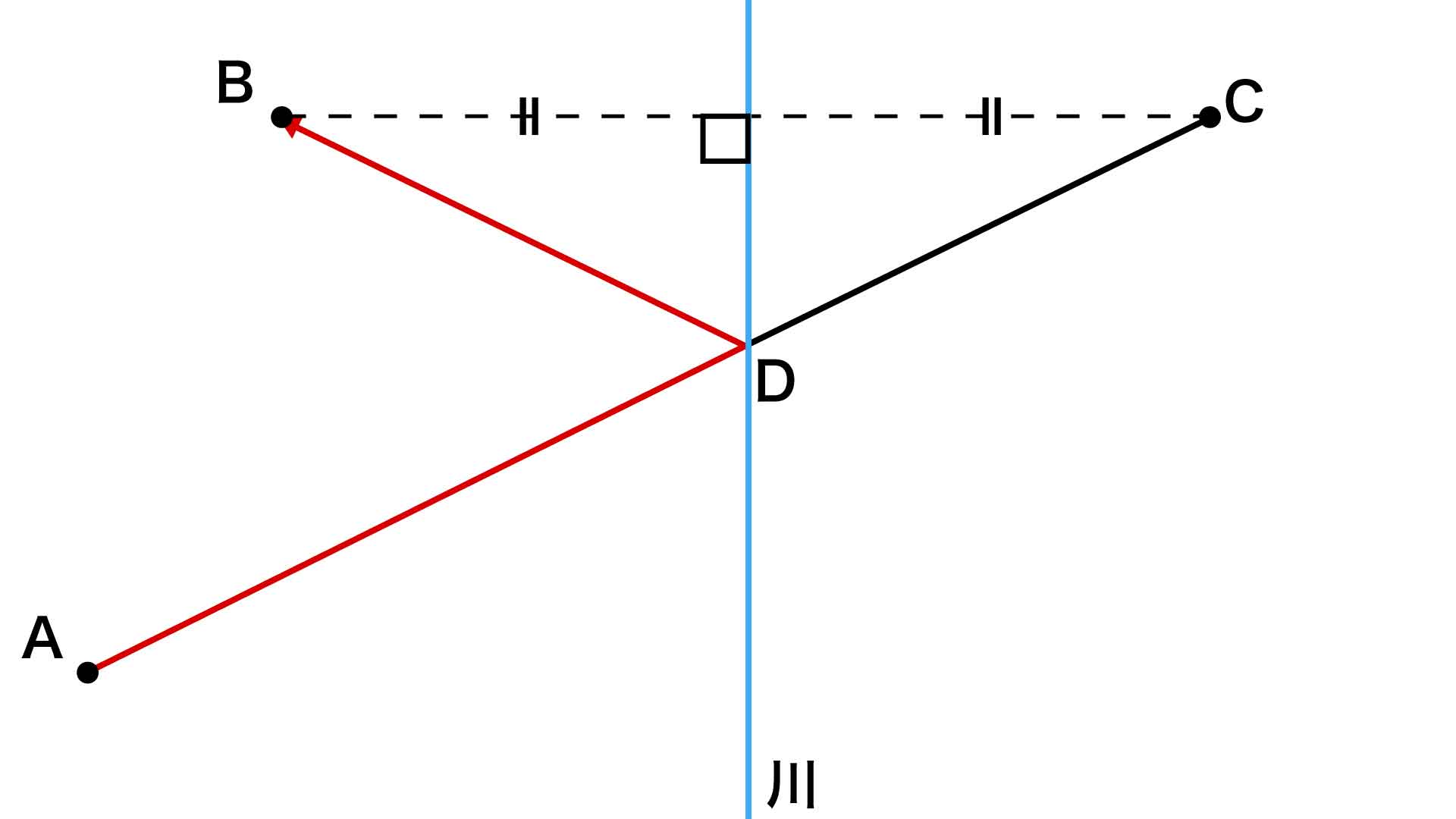
ここで、「A地点から東に100km」の地点をE地点、「A地点から東に160km」の地点をF地点とします。角DAE=角CAF、角DEA=角CFA=90度であることから、三角形ADEと三角形ACFは3つの内角がそれぞれ等しく、相似であることがわかります。
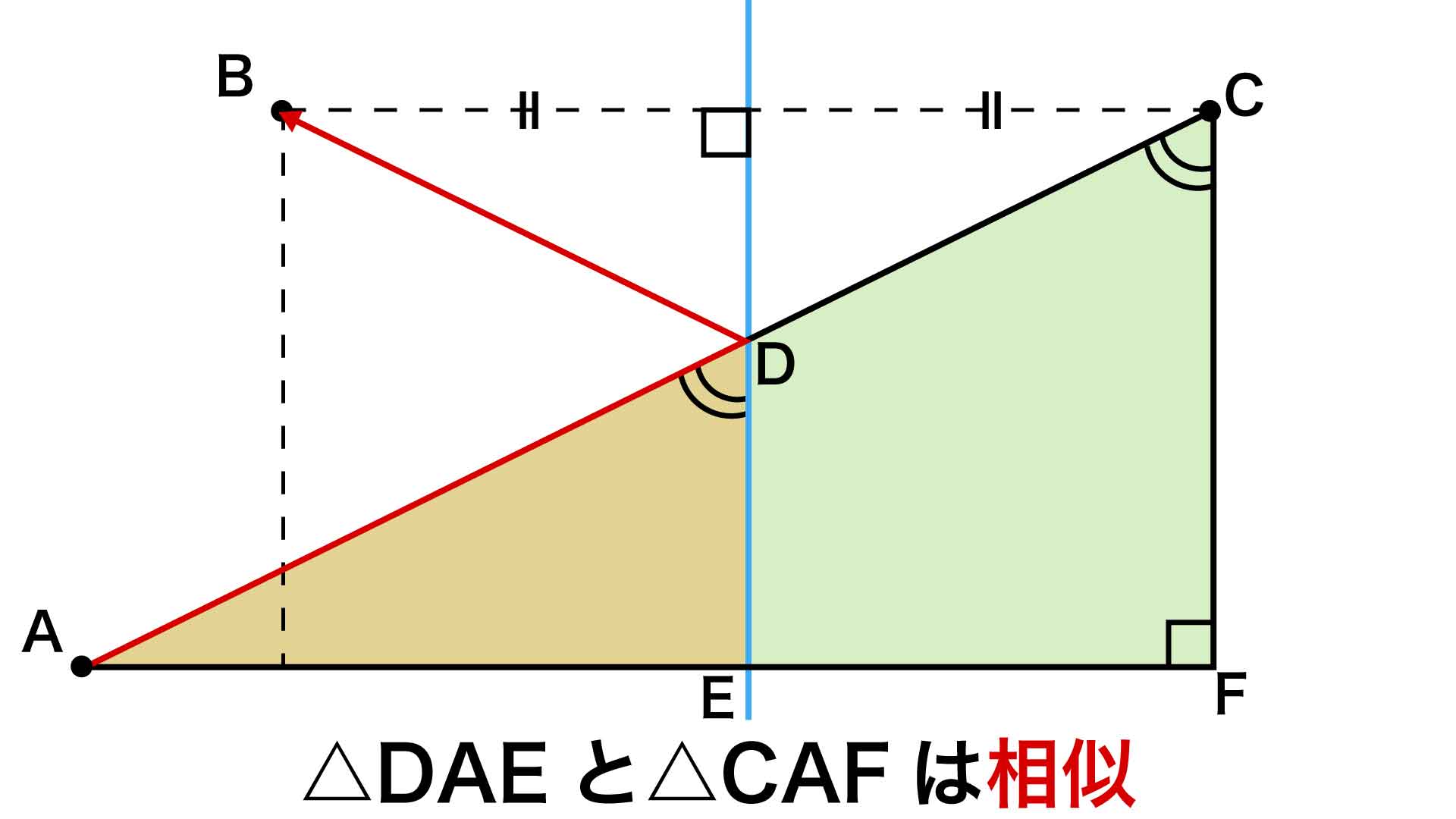
AEはAFの100/160=5/8倍の長さであることから、DEの長さはCFの長さの5/8倍です。
CFの長さが120kmであることから、DEの長さは120km×(5/8)=75kmとなります。
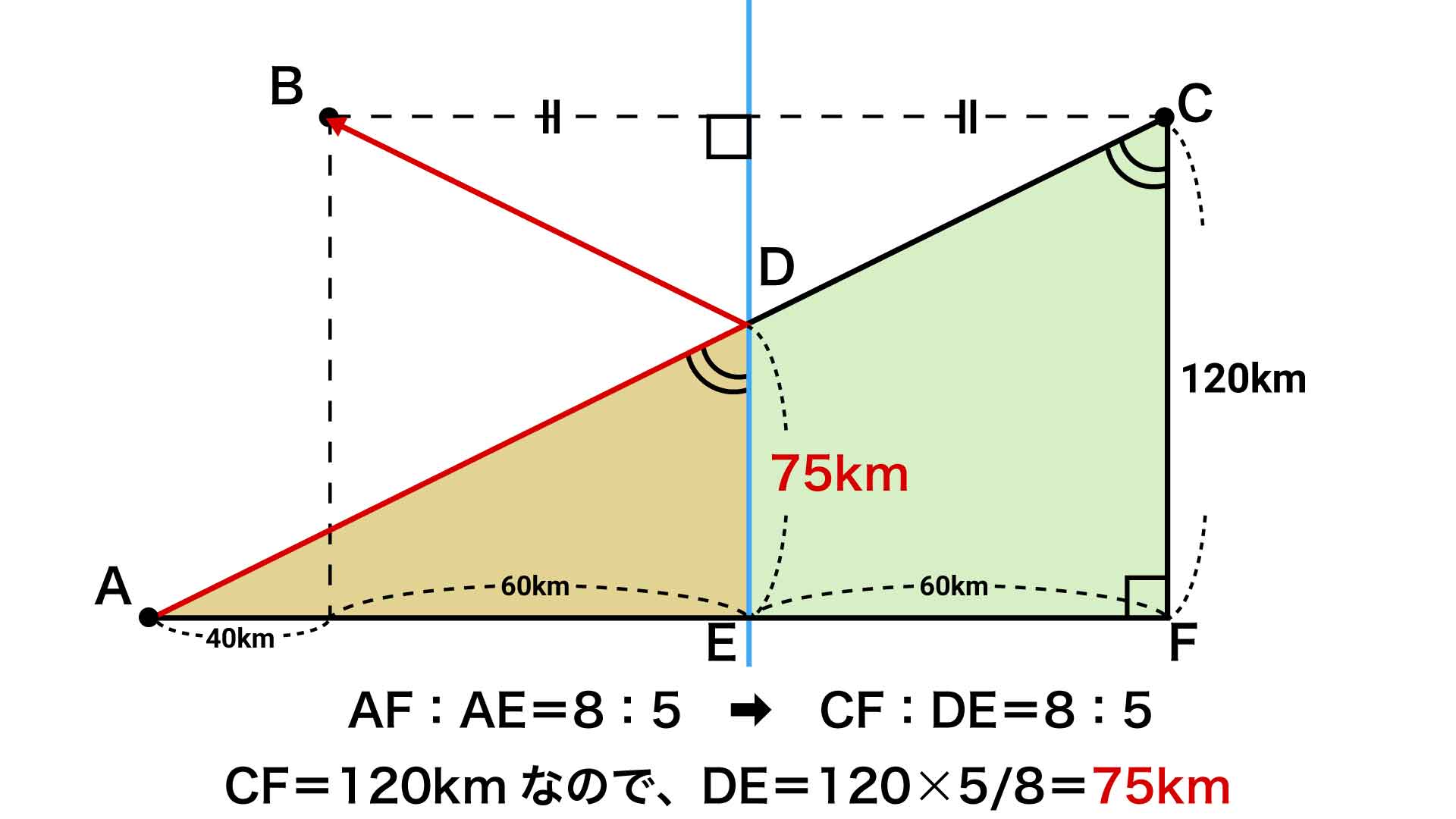
したがって、移動距離が最短になるときのD地点は、A地点から「東に100km、北に75km」の地点となります。
答え：75km
「ひらめけ！算数ノート」のバックナンバーはこちら！
【前回の算数ノートはこちら】
【あわせて読みたい】
