解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです。
今回の解き方をまとめた図がこちらです。
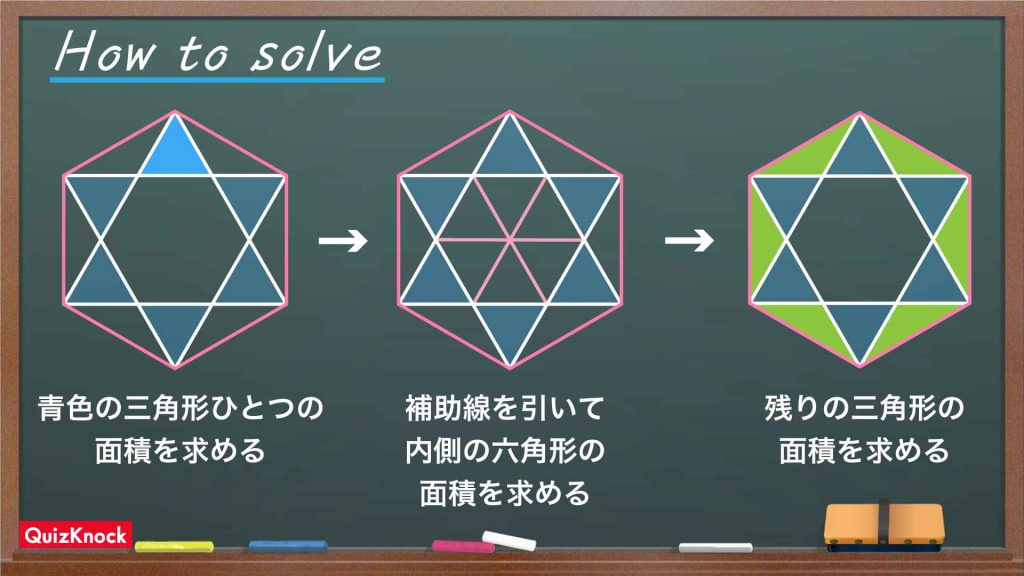
今回のポイントは、「青色の正三角形と等しい面積の三角形を見つけること」です。
この流れに沿って、問題を攻略していきましょう!
青色の三角形の性質を調べる
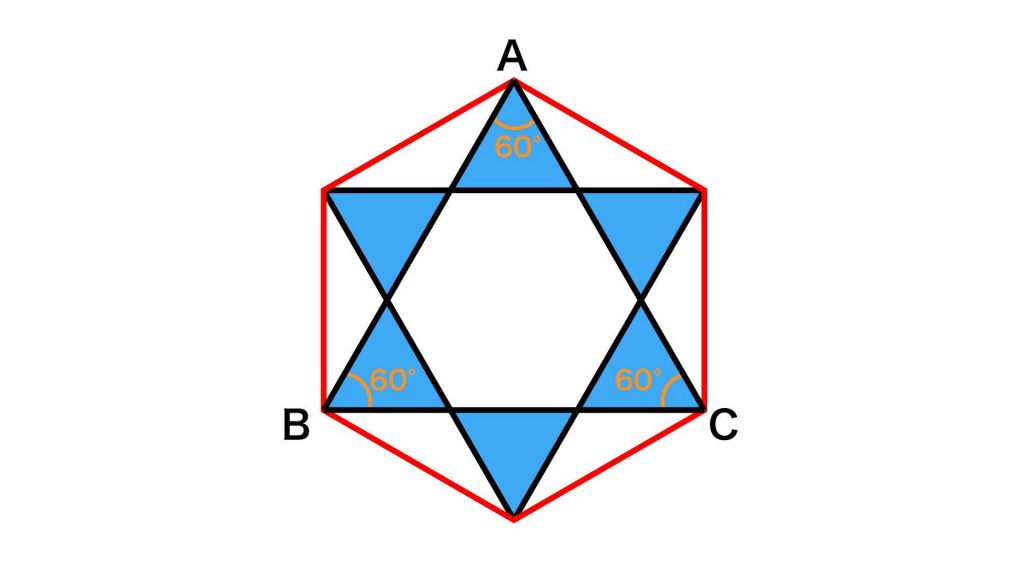
まずは、青色の三角形の性質を調べます。下の図のように、各点をA,B,C,D,Eとします。
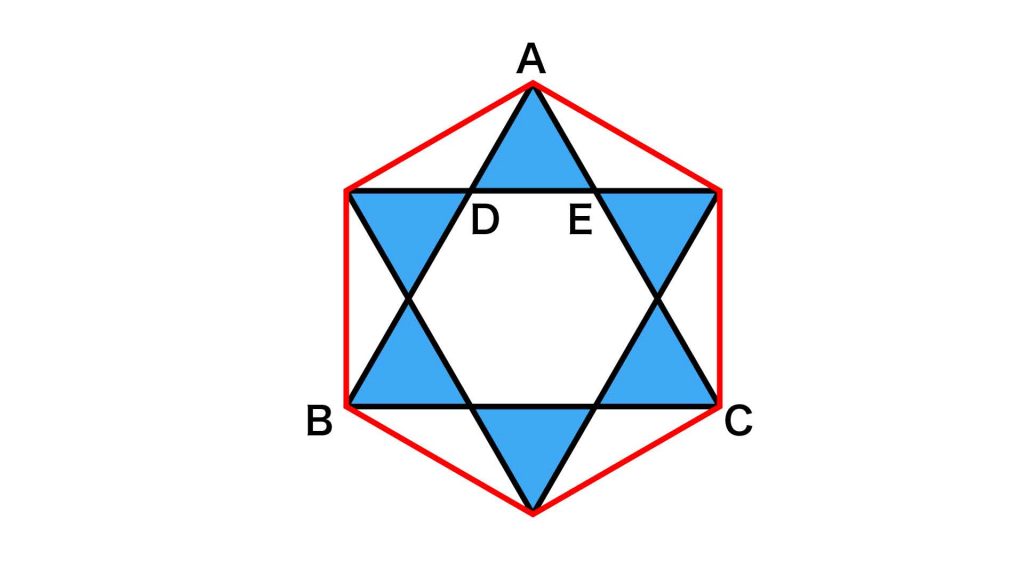
正六角形において、1つの頂点を間に挟む、2つの頂点を結ぶ対角線の長さは等しくなります。つまり、AB=BC=CAです。3辺の長さがすべて等しいので、三角形ABCは正三角形とわかります。
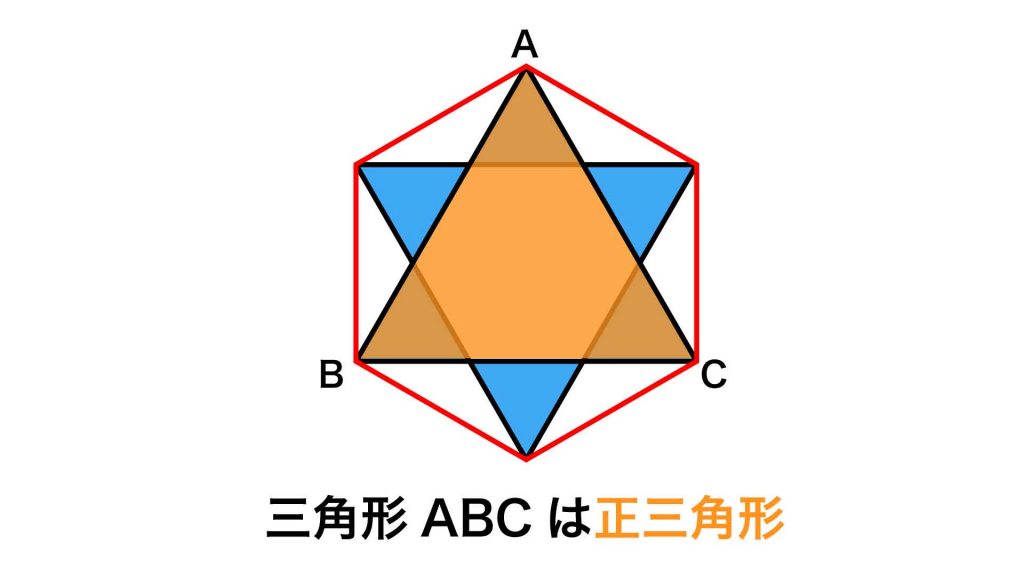
したがって、角ABC=角ACB=角BAC=60度となります。
また、下の図において、DEとBCは平行になります。平行線の同位角の大きさは等しいので、角ABC=角ADE=60度、角ACB=角AED=60度となります。
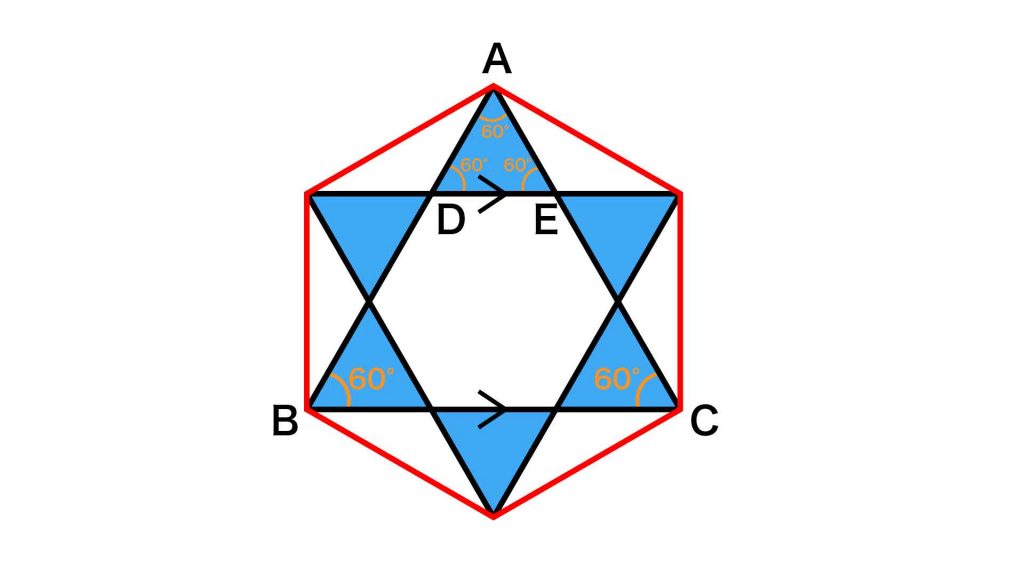
したがって、内角の大きさがすべて60度であるので、三角形ADEは正三角形だとわかります。
同様に考えると、他の青色の三角形もすべて正三角形であるといえます。
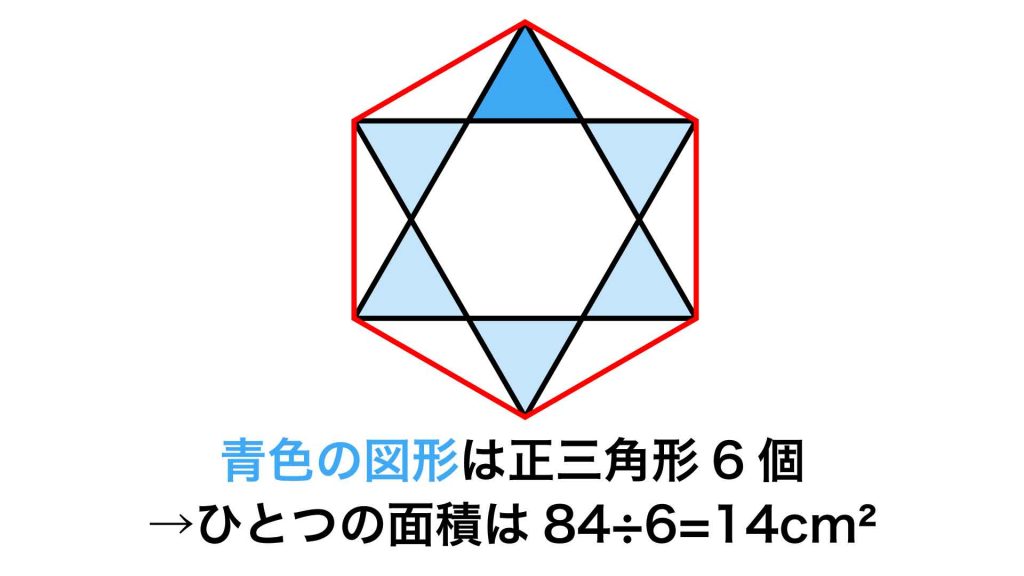
さらに、内側の白い六角形は、内角の大きさがすべて120度であることから、正六角形です。したがって、6つの青色の正三角形の辺の長さがすべて等しくなるので、6つの青色の正三角形はすべて同じ面積であることがわかります。
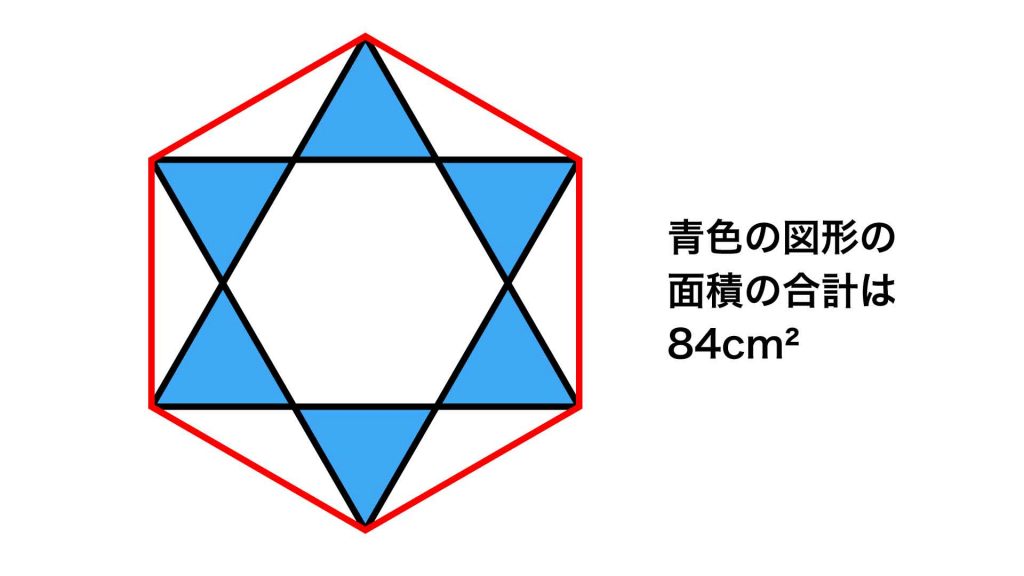
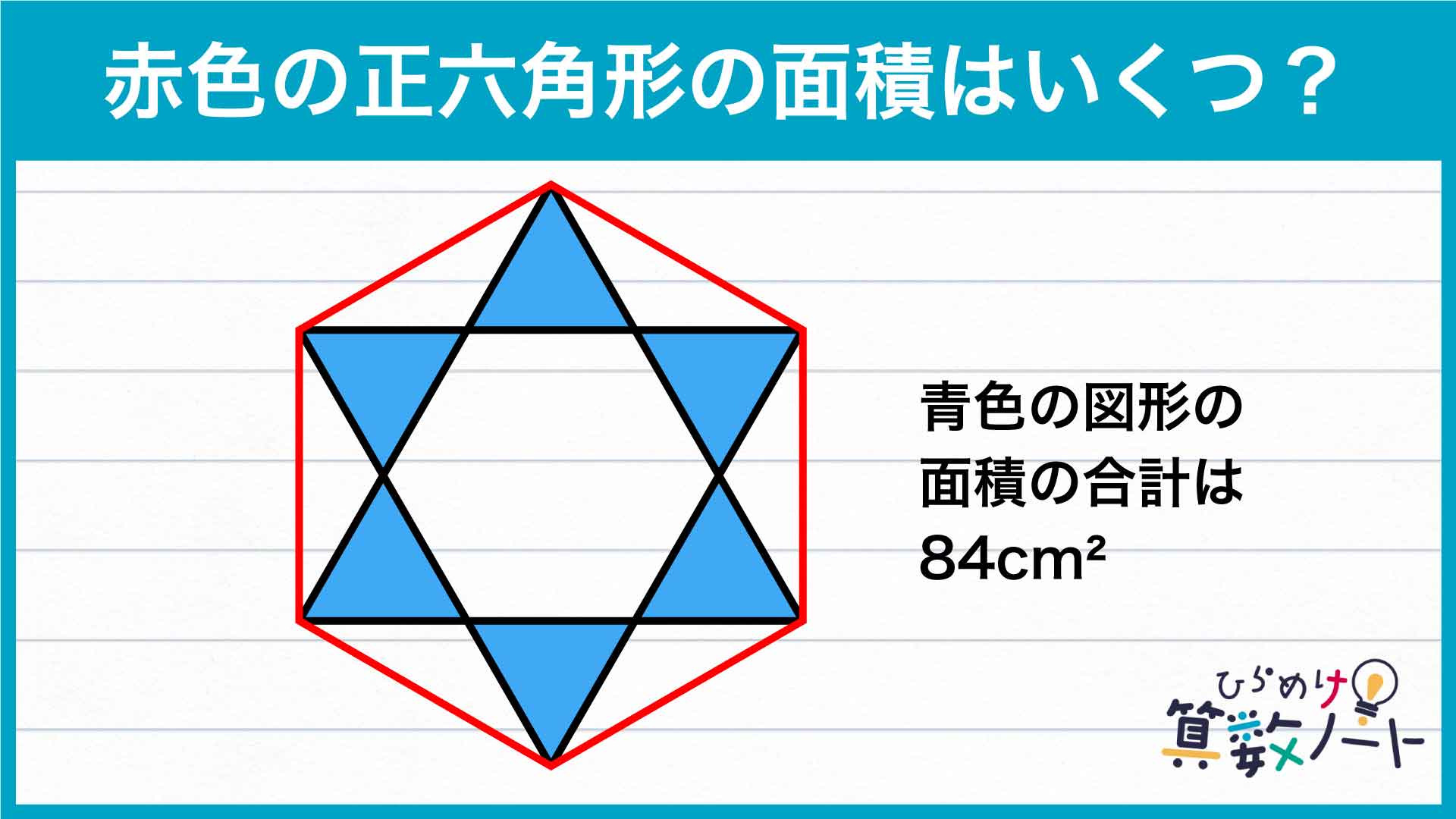
青色の図形には同じ面積の正三角形が6個含まれており、その合計面積は84cm2と与えられています。したがって、青色の正三角形1つ分の面積は84÷6=14cm2です。
補助線を引く
下の図のピンク色の線のように、内側の正六角形に補助線を引きます。
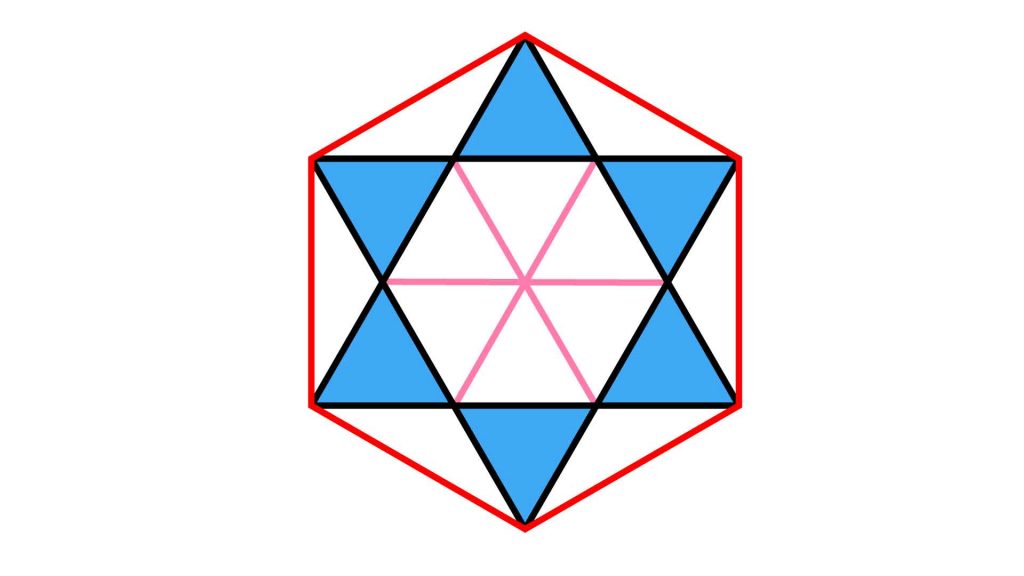
正六角形の向かい合う頂点を結んだ対角線は、内角を二等分する性質があります。正六角形の1つの内角の大きさは120度なので、ピンク色の対角線により、大きさが60度の角が2つできます。補助線を引いてできた三角形の2つの角の大きさが60度なので、残る角の大きさも60度です。
したがって、正六角形に補助線を引いてできた三角形は、3つの角が等しいため正三角形だとわかります。
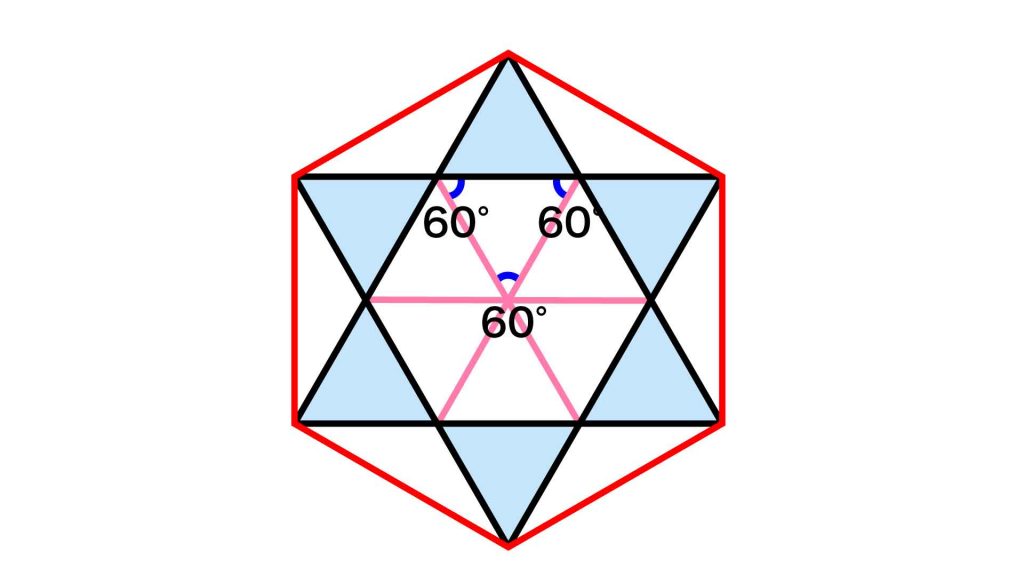
ここで、一組の青色の三角形と、内側の三角形について考えます。
青色の正三角形と内側の正三角形は、一辺を共有しています。つまり、すべての辺の長さが等しいため合同です。
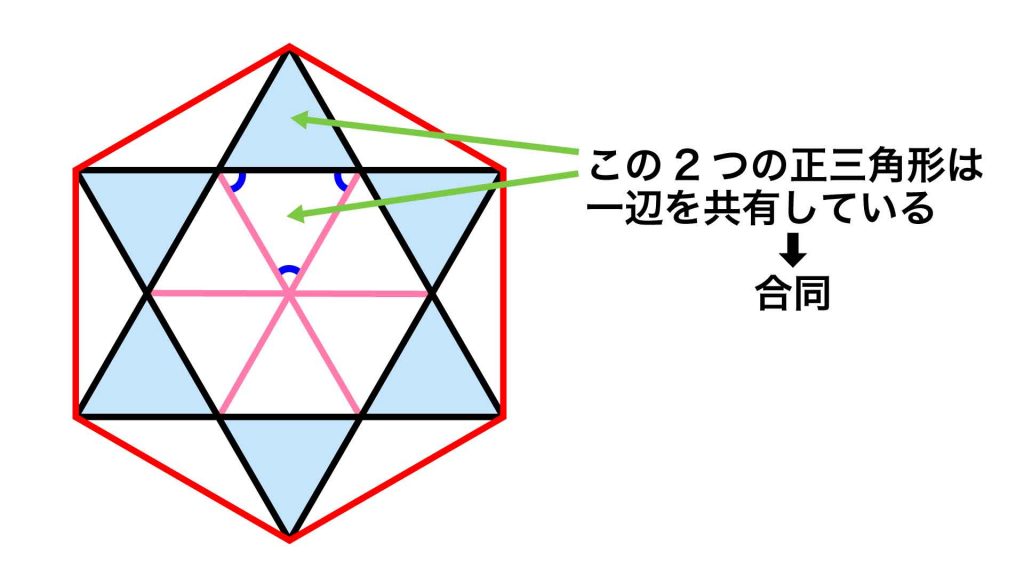
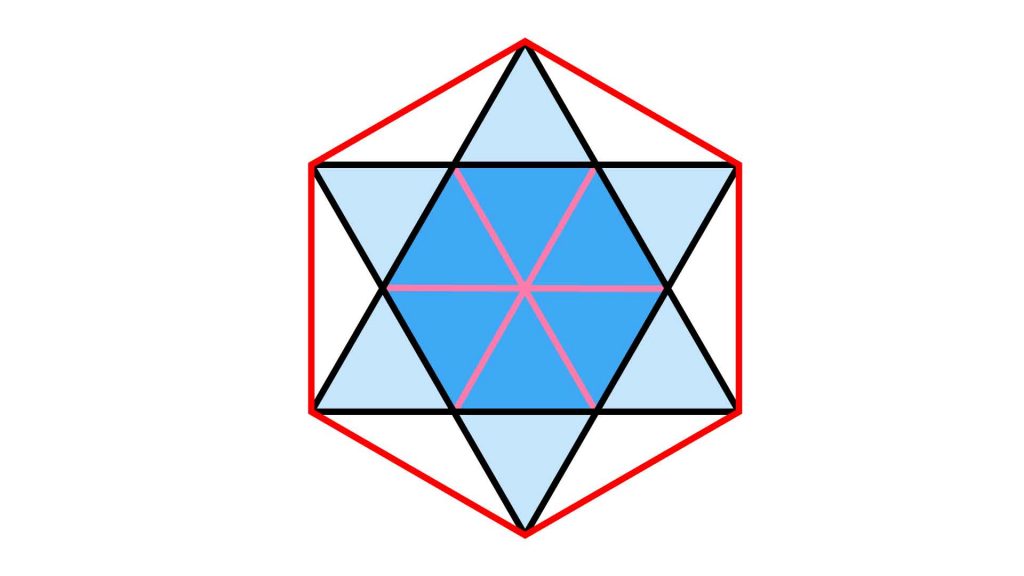
したがって、内側の正六角形の面積は、青色の正三角形6個の面積と等しいことがわかります。
残りの三角形の面積を求める
ここからは、残りの三角形の面積を求めます。下の図のように、残りの三角形を緑色の三角形とします。
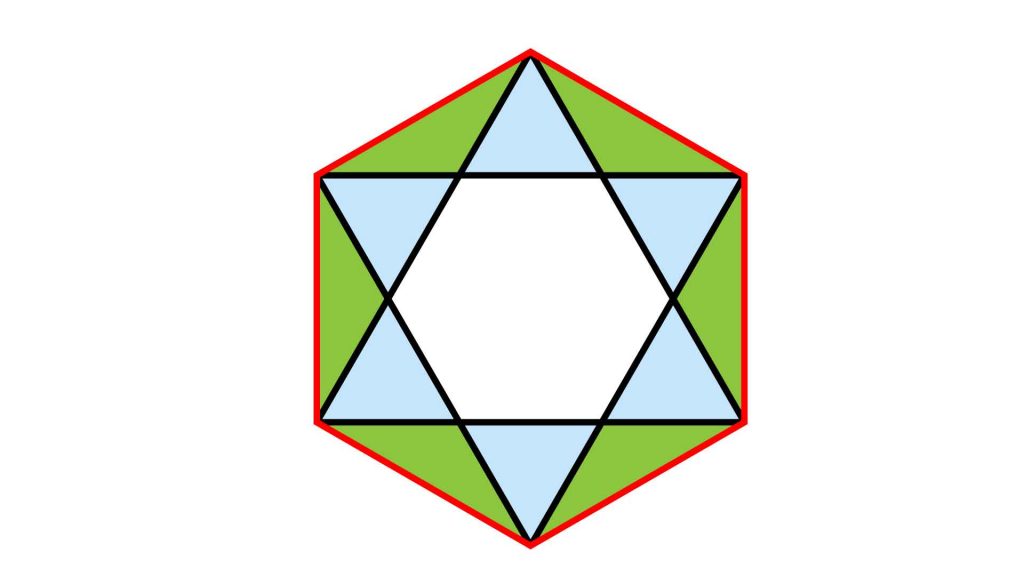
ここで、一部の青色の正三角形と緑色の三角形に注目します。
緑色の三角形と青色の正三角形は、底辺を共有しており、かつ高さが等しくなっています。したがって、緑色の三角形と青色の正三角形の面積は等しいことがわかります。
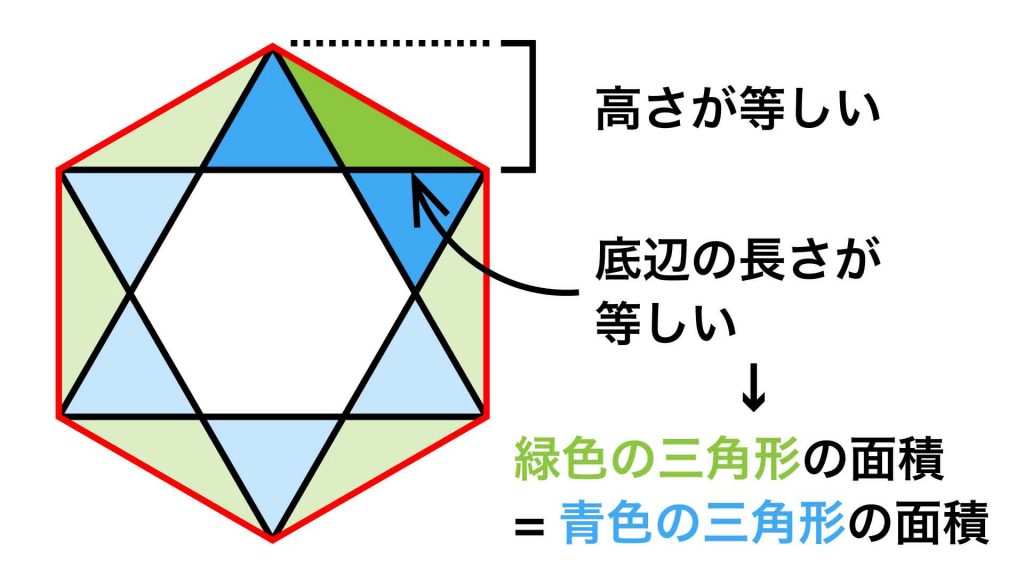
以上より、緑色の三角形の合計の面積も、青色の正三角形6個の面積と等しいことがわかります。
求める面積は、青色の正三角形18個分
以上より、赤色の正六角形の面積は、青色の正三角形18個分の面積と等しいことがわかります。
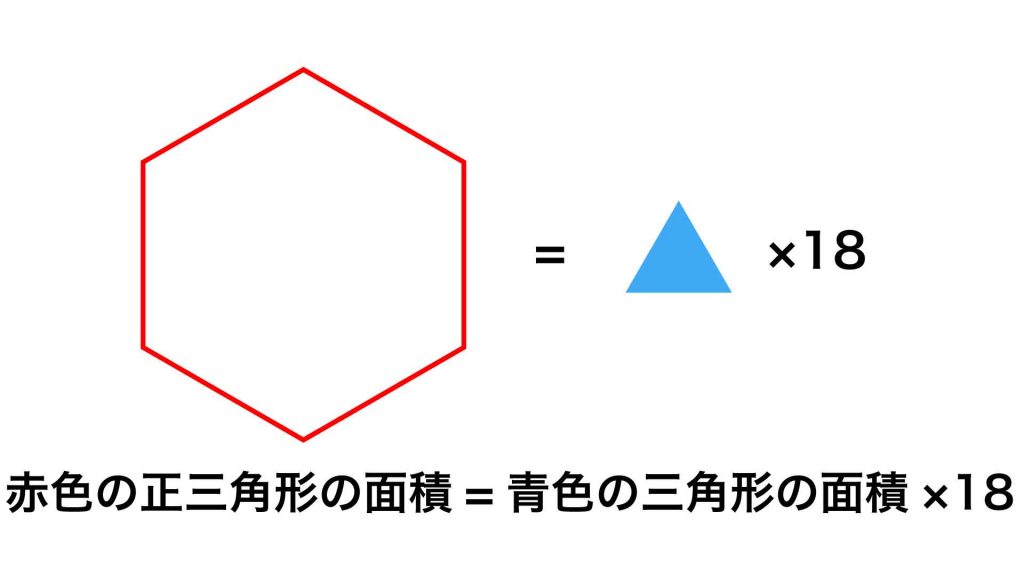
したがって、赤色の正六角形の面積は、14×18=252cm2となります。
答え:252cm2
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)









.jpg)







