小学生で解ける「面積と比」の問題、補助線がカギ！

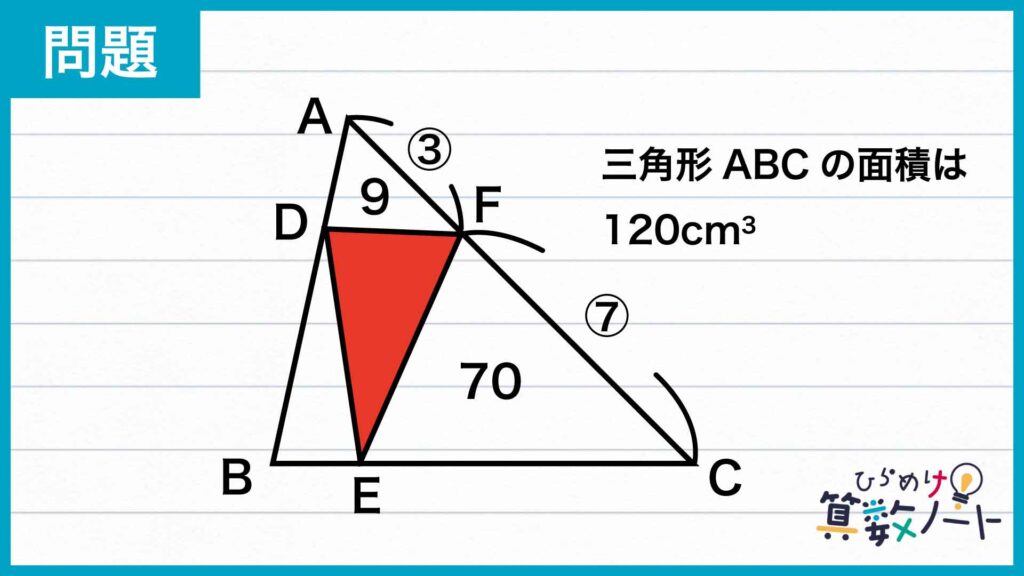
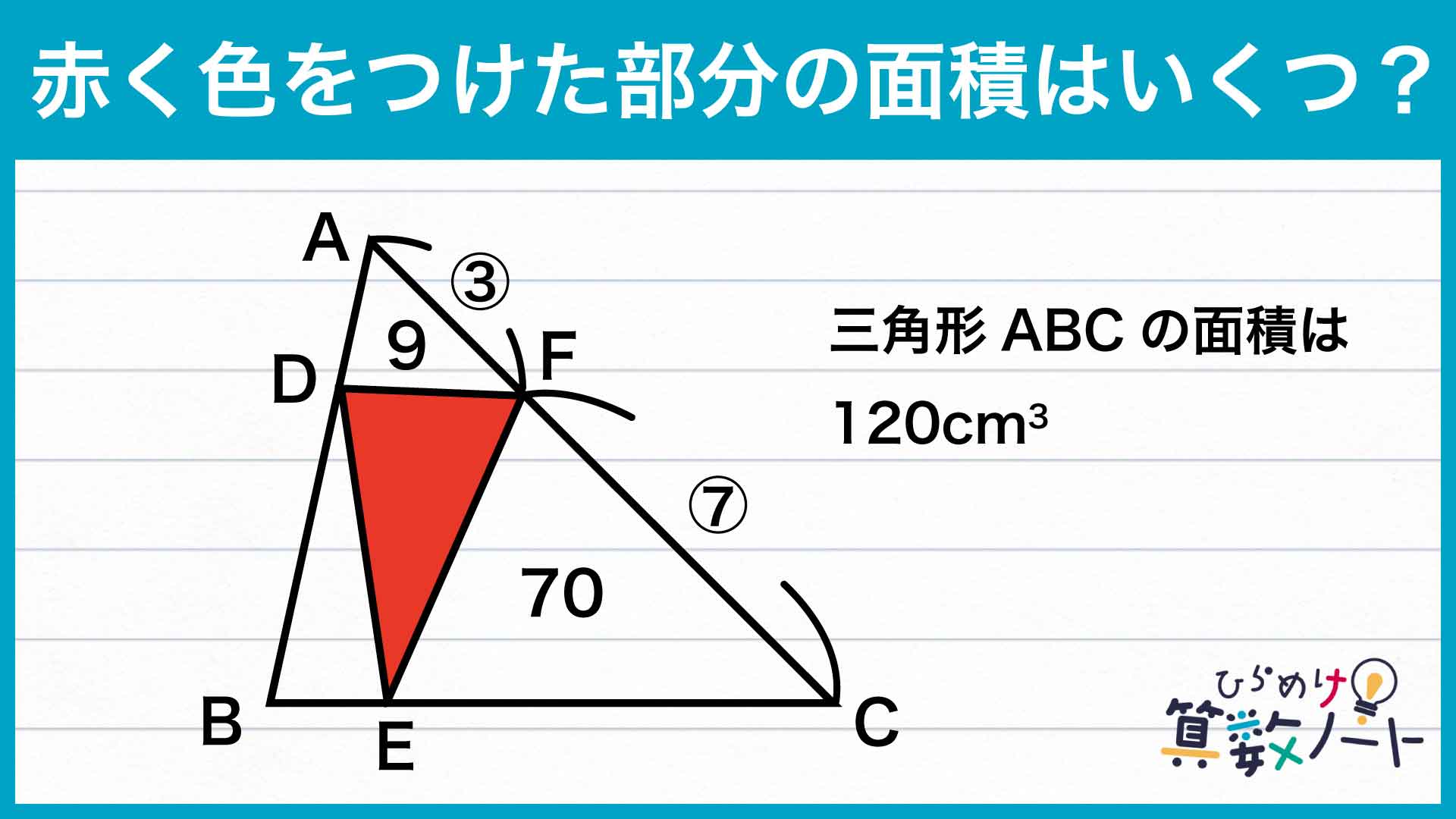
問題はこちら

1ページ：【解答フォーム】自力で解きたい方はこちらへ！　以下は問題の解説です

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

この問題の解き方をまとめた図がこちらです。

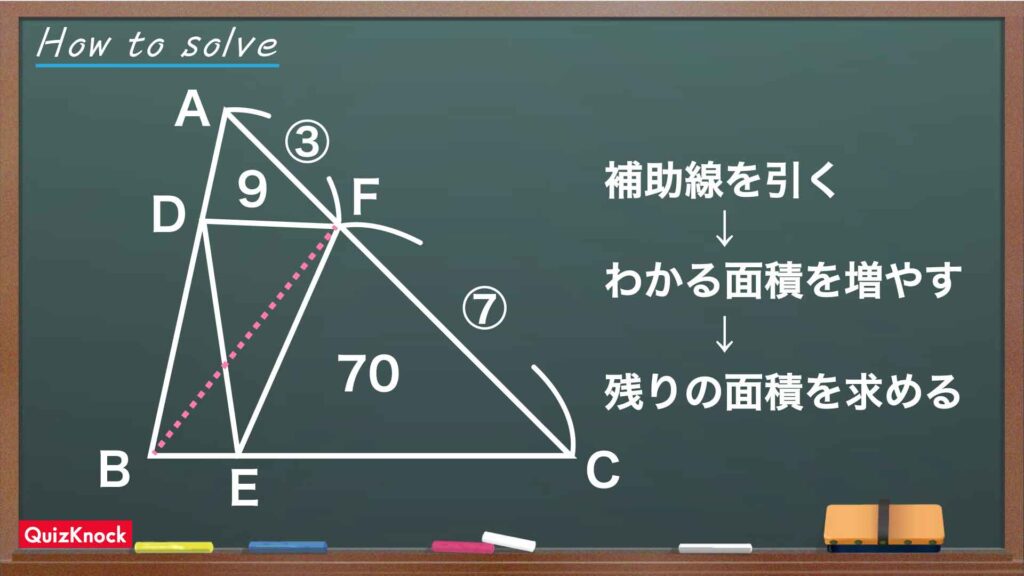
今回のポイントは「辺の比から、面積の比を順番に広げていくこと」です。

このポイントをもとに、問題を攻略していきましょう！

AF：FCの比から、三角形を分ける

同じ高さをもつ三角形では、底辺の長さの比＝面積の比になります。

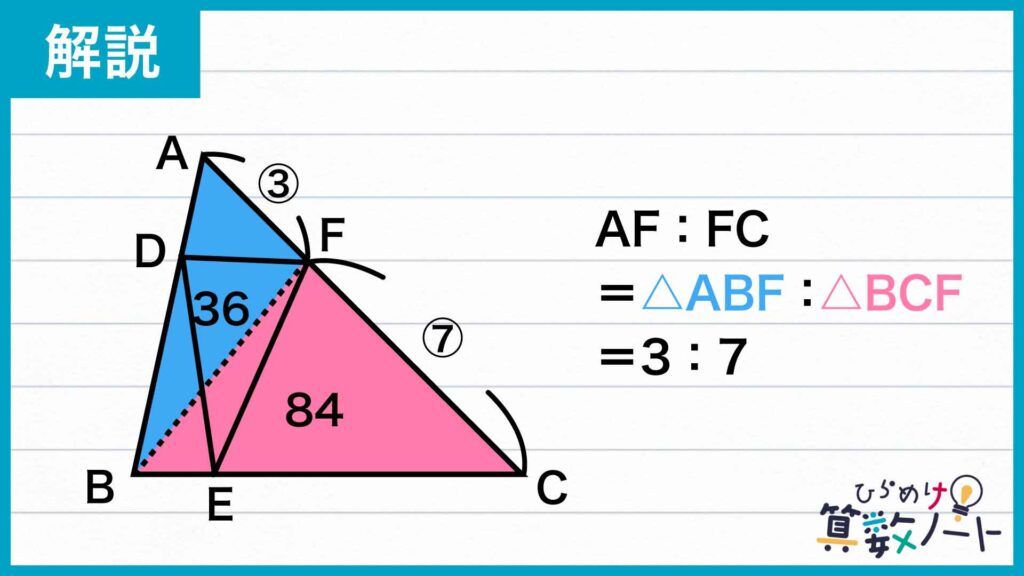
AF：FC=3：7なので、三角形ABC（120cm²）はこの比で分けられます。

• 三角形ABF：36cm²
• 三角形BCF：84cm²

面積から、辺の比を見つける

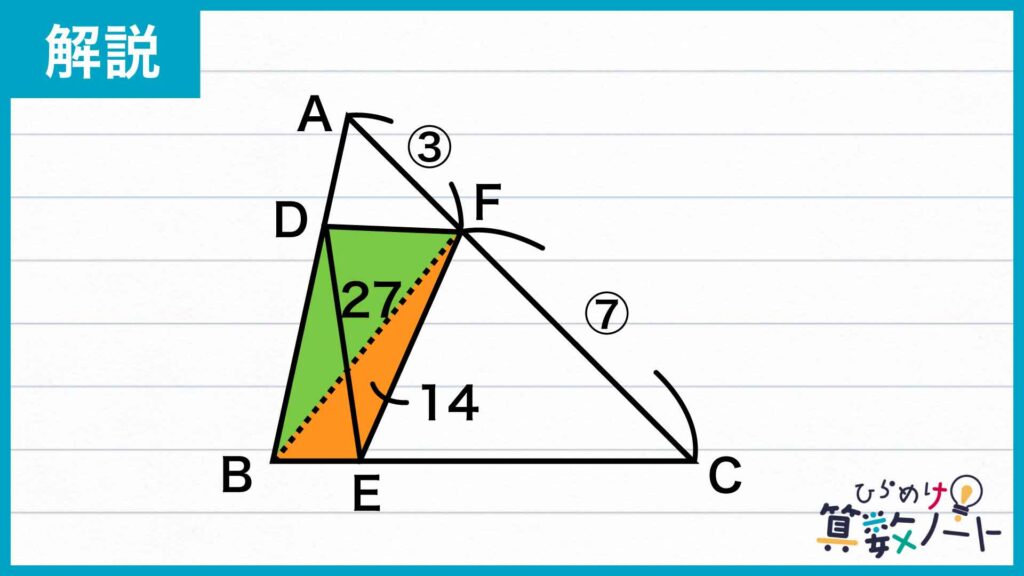
三角形ABFの中で三角形ADFの面積は9cm²なので、三角形BDFの面積は36−9=27cm²です。

同様に、三角形BCFの中では三角形CEFが70cm²なので、三角形BEFの面積は84−70=14cm²となります。

それぞれの面積が求まったことで、先程とは逆に面積の比から辺の比を求めることができるので、

• AD：DB=1：3
• BE：EC=1：5

であることがわかります。

全体から引いて、答えを出す

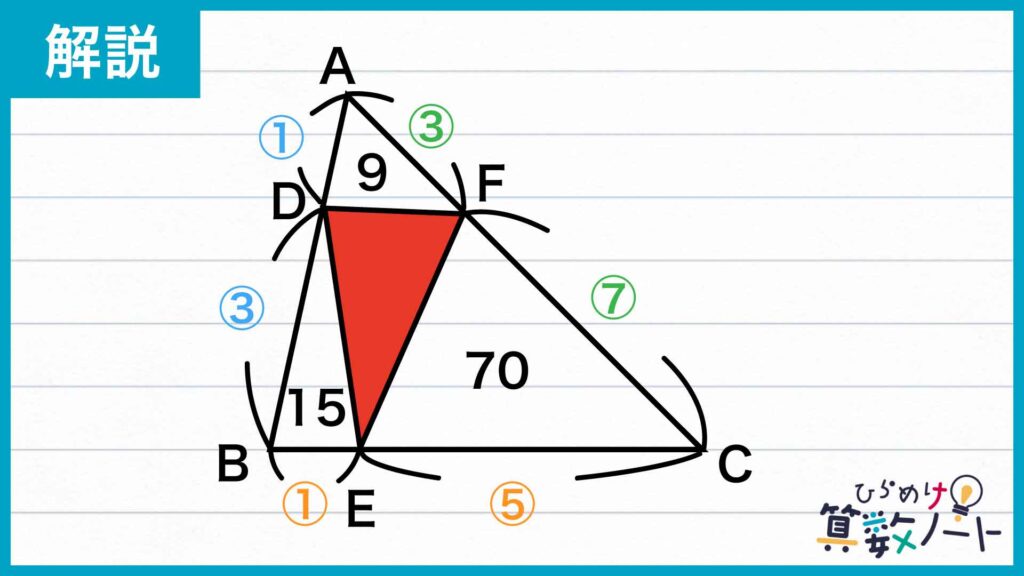
点DとEの位置がわかったので、三角形BDEの面積を求めます。これまでと同様に、同じ高さをもつ三角形では、底辺の比がそのまま面積の比になることを利用しましょう。

まず、AD：DB=1：3なので、点Dは辺ABを1：3に分ける位置にあります。つまり、三角形ABCを線分DCで分けると、三角形BCDは三角形ABCの3/4です。

同様に、BE：EC=1：5なので、点Eは辺BCを1：5に分ける位置にあり、BからEまでの長さは全体の1/6になります。

そのため、三角形BDEの面積は三角形BCDの面積の1/6となり、120×3/4×1/6=15cm²と求めることができます。

最後に、三角形ABCからわかっている面積をすべて引きます。

120−9−70−15＝26cm²

これが、三角形DEFの面積です。

答え：26cm²

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】