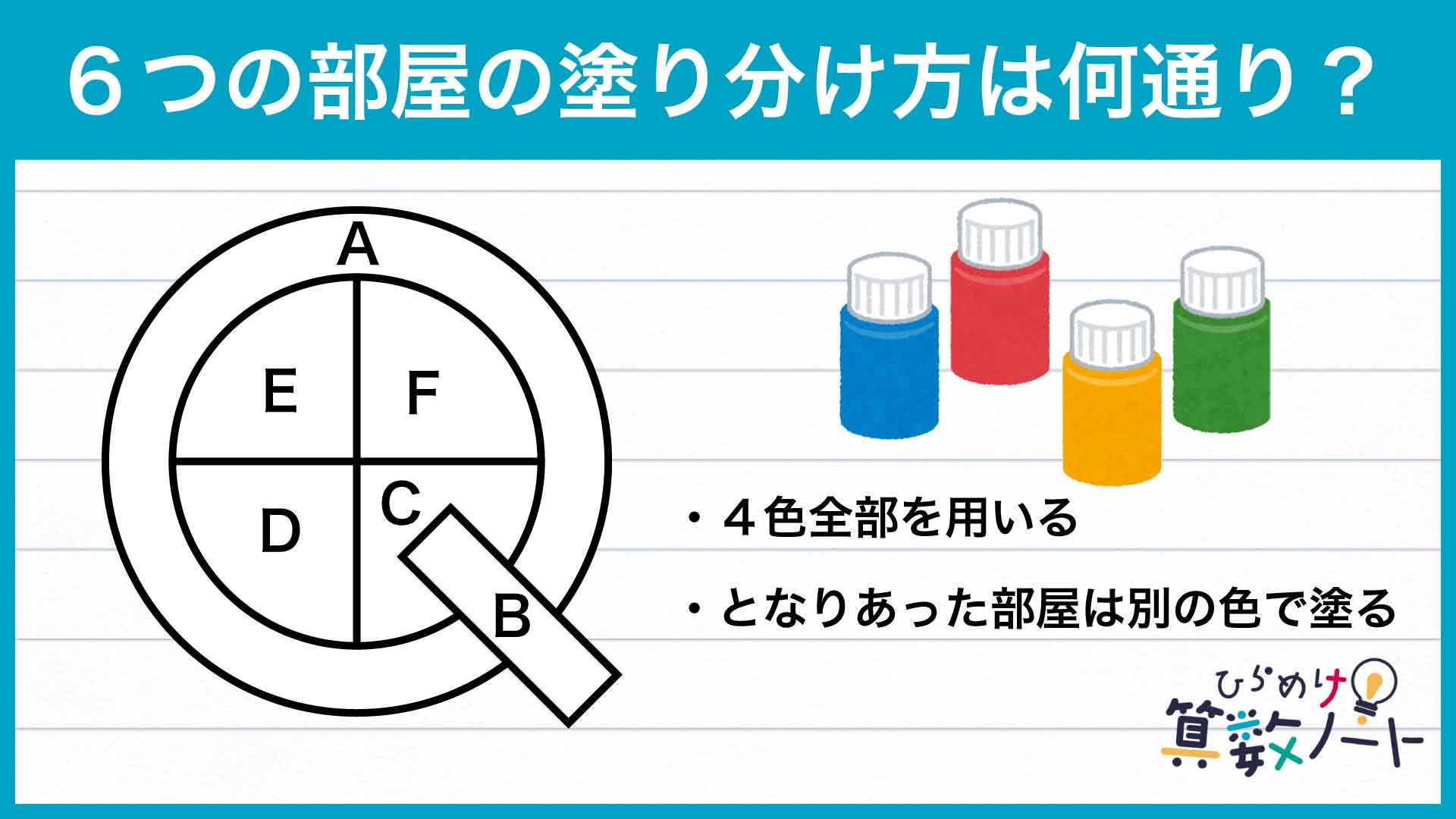
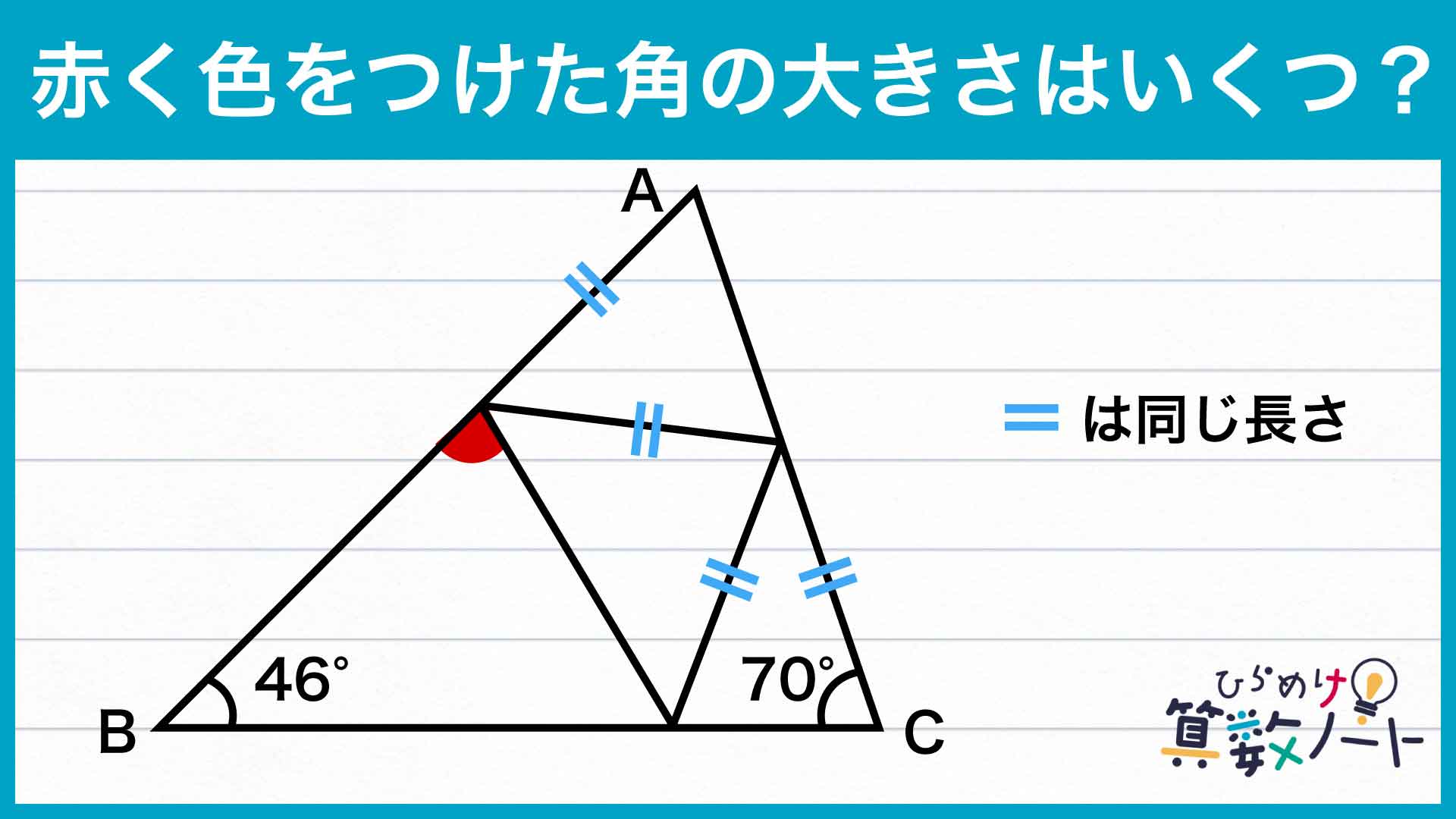
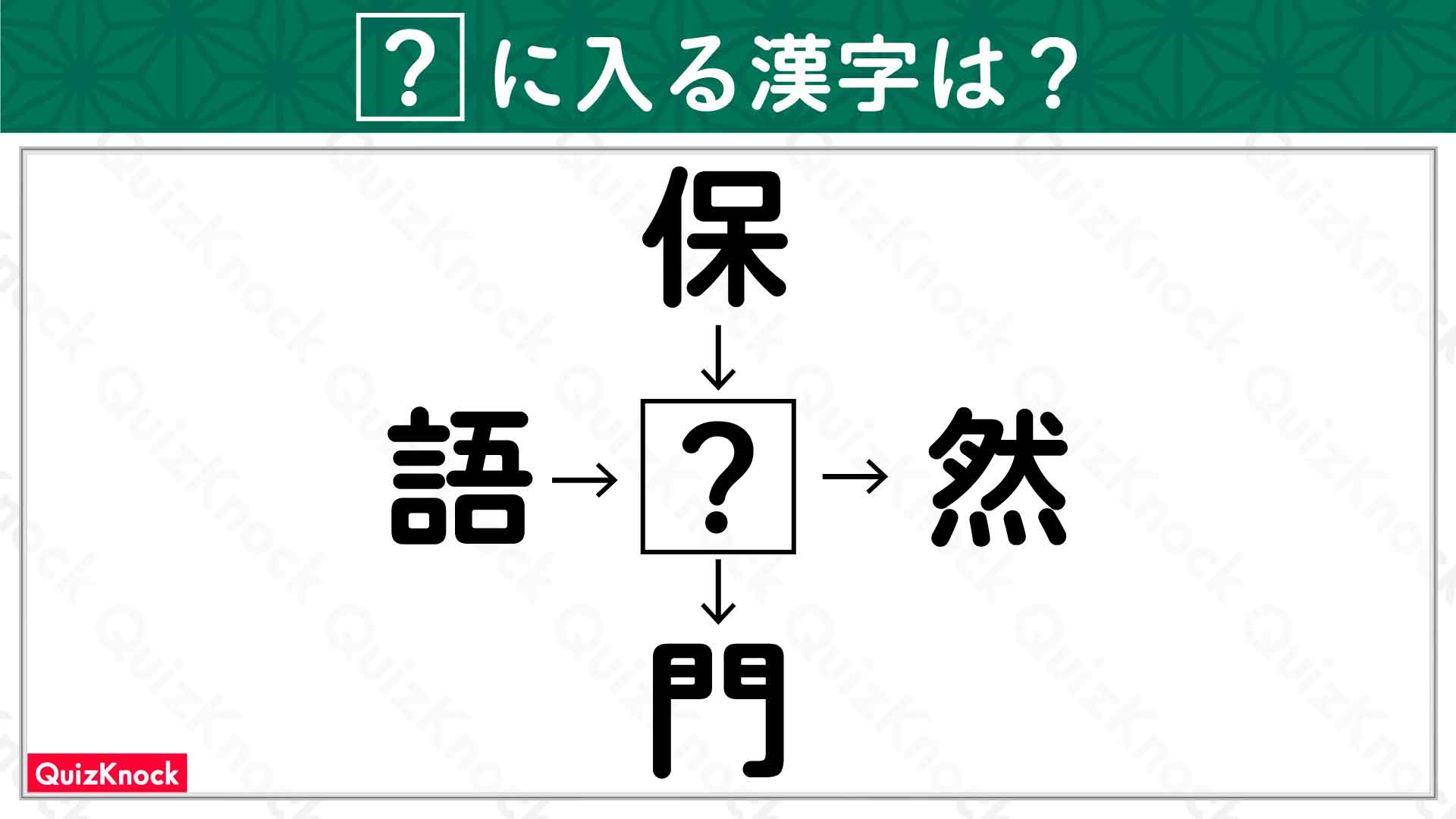
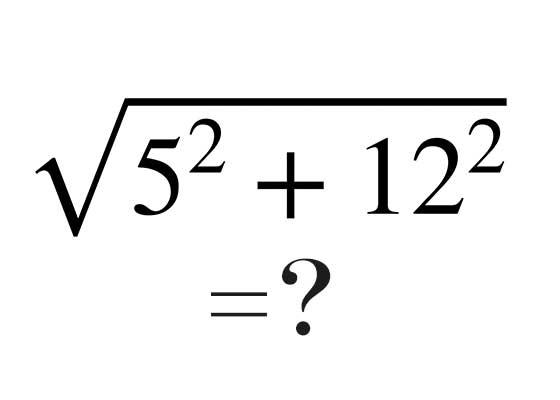コジマです。
京大入試珍問ランキングを作ったら絶対にトップ5に入るであろう問題がある。
tan1°は有理数か。
[06 京都大(後期)]
タンジェント1°が有理数かどうかを示し、それを証明する問題だ。問題文は本当にこれだけで補足などは一切なく、当時の受験生は面食らったことだろう。
これを証明するには、問題文に出てくる「有理数」のことを正しく理解していなければいけない。有理数って何だ?
「有理数」=「分数の形で表せる数」
「2つの整数a, bを用いてb/aの形で表せる数」を総称して有理数という。
整数
例えば1, 2, 3, ……と続く整数は、いずれも1/1, 2/1, 3/1, ……と表せるので有理数である。
有限小数
また、有限小数(桁の数が有限個な小数)はすべて分数の形で表せる。
例えば3.46という小数は、3.46=346/100=173/50と変形できるので有理数。
循環小数
さらに、循環小数(同じ並びが繰り返される小数)もすべて有理数。
例えば3.464646…という小数は、これをaとおけば、
100a = 346.464646… (1)
a = 3.464646… (2)
(1)から(2)を引いて99a = 343, a=343/99
と変形できて、3.464646...=343/99となる。
有理数でない数は「無理数」
何だどれも有理数じゃないか、と思うかもしれないが、有理数でない数も存在する(※)。このような数を無理数という。
※むしろ無理数のほうが数としては多い
無理数で一番分かりやすいのが2の正の平方根、√2。√2は1.41421356...と小数で表せるが、循環はしない。無理数を小数で表すと必ず非循環小数になるし、逆に非循環小数ならばそれは無理数だ。例えば円周率もネイピア数(自然対数の底)も無理数である。
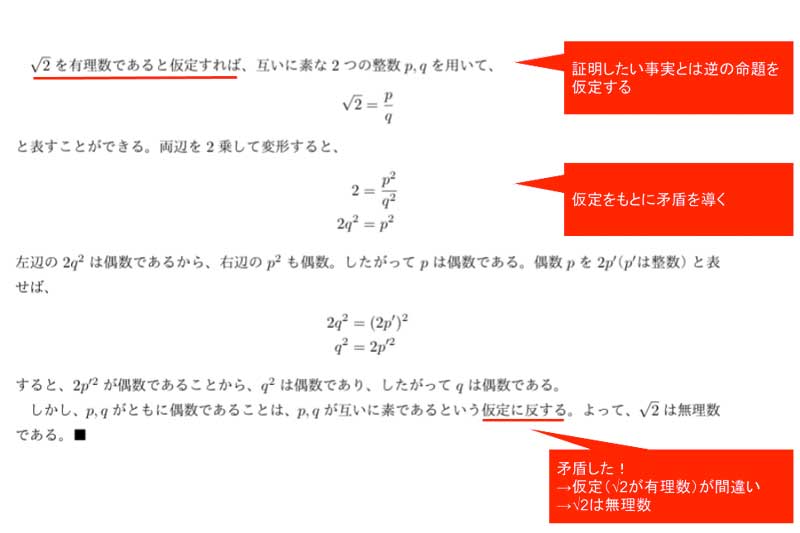
√2が無理数であることの証明は、証明法のひとつ・背理法の代表例としてよく知られている。
冒頭の入試問題も√2と同じように、tan1°を有理数と仮定することで背理法で証明できる。数学力をつけたい人は一度挑戦してみるべし。
ちなみに、無理数は何が「無理」なのだろう。
英語では、有理数が“rational number”、無理数が“irrational number”。“rational”を辞書で引くと「合理的な」という意味があるが、ここでは「比(ratio)の」という意味。
ところが日本語に訳す際、rationalを「合理的な」の意味でとって「有理数」とした。その対義語だから「無理数」となるが、そうしたら「無理」=“impossible”みたいになって……と、要するに何も無理ではないのである。
用語を誤解なく訳すのは結構大変なのだ。











.jpg)