小学生でできる「正方形と動く点P」の問題、あなたは解ける？

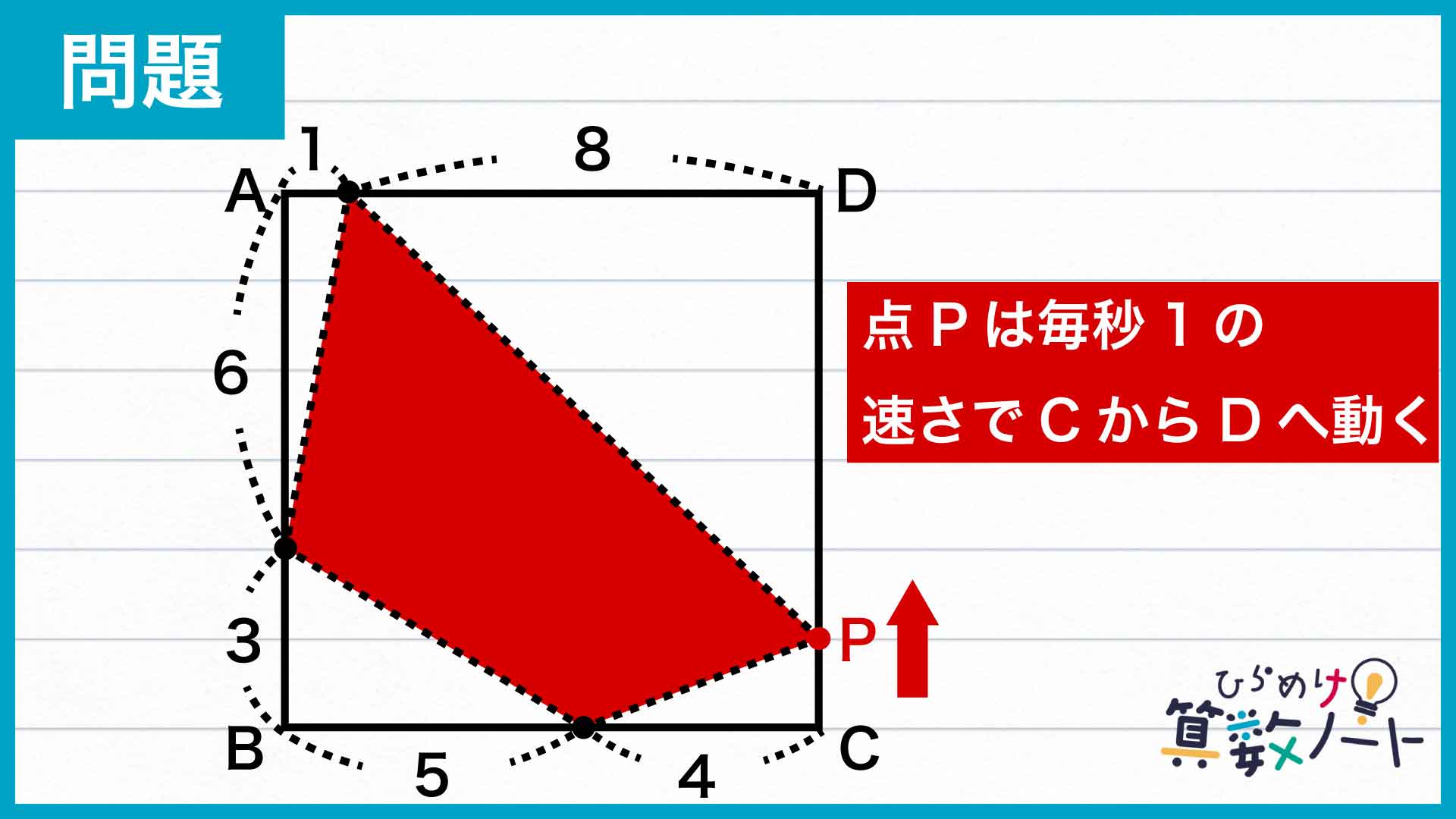
問題はこちら

1ページ：【解答フォーム】自力で解きたい方はこちらへ！　以下は問題の解説です

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

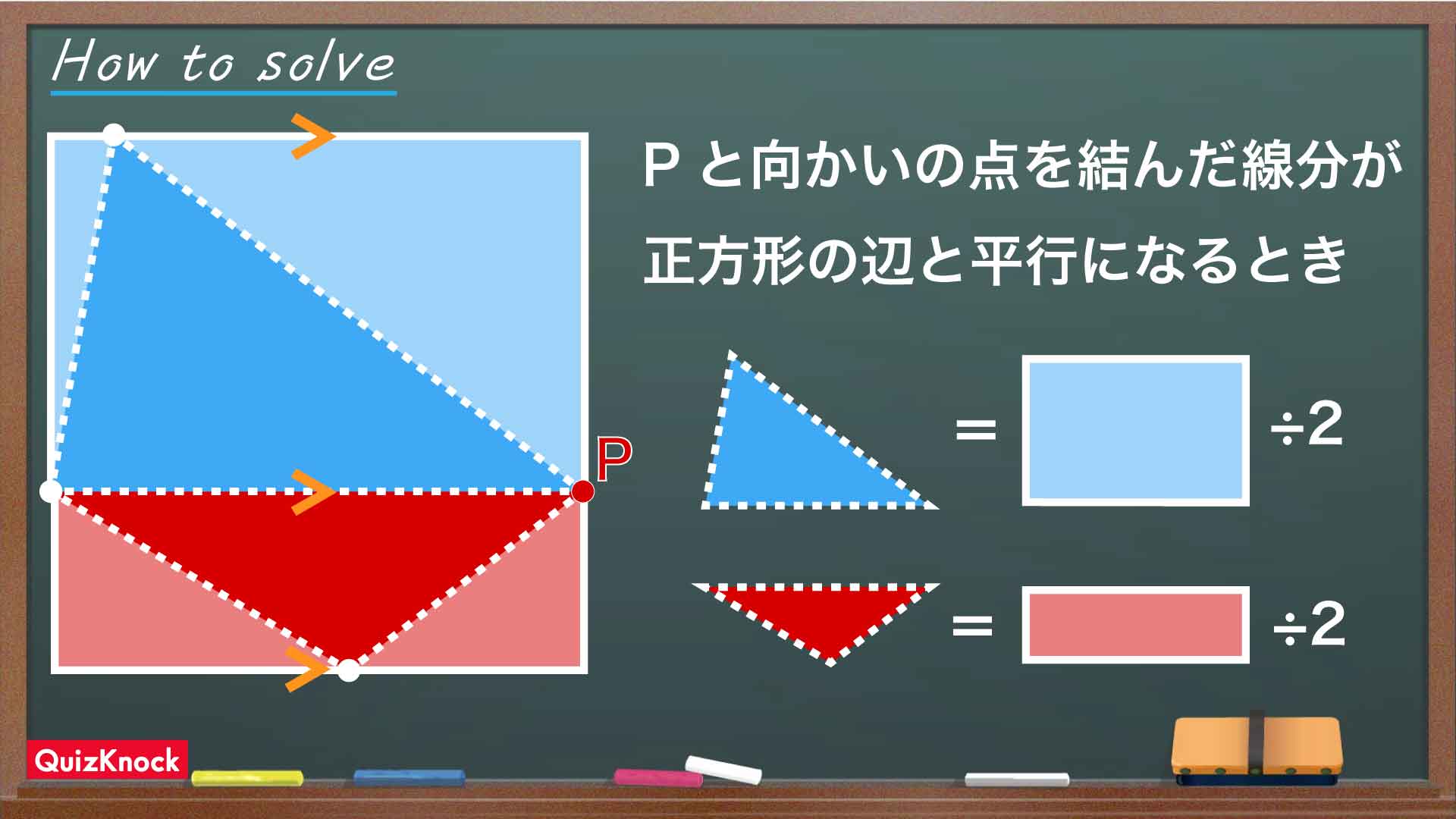
この問題の解き方をまとめた図がこちらです。

大切なのは、四角形の面積が正方形の半分になる「ゴール」の状況をきちんとイメージすることです。

では、このポイントを踏まえて解いていきましょう！

条件に合う状況をイメージする

今回の問題では、点Pの動きとともに変化していく四角形の面積を逐一追っていてもキリがありません。まずは、実際に四角形の面積が正方形ABCDの半分となった「ゴール」の状況をイメージしてみましょう。

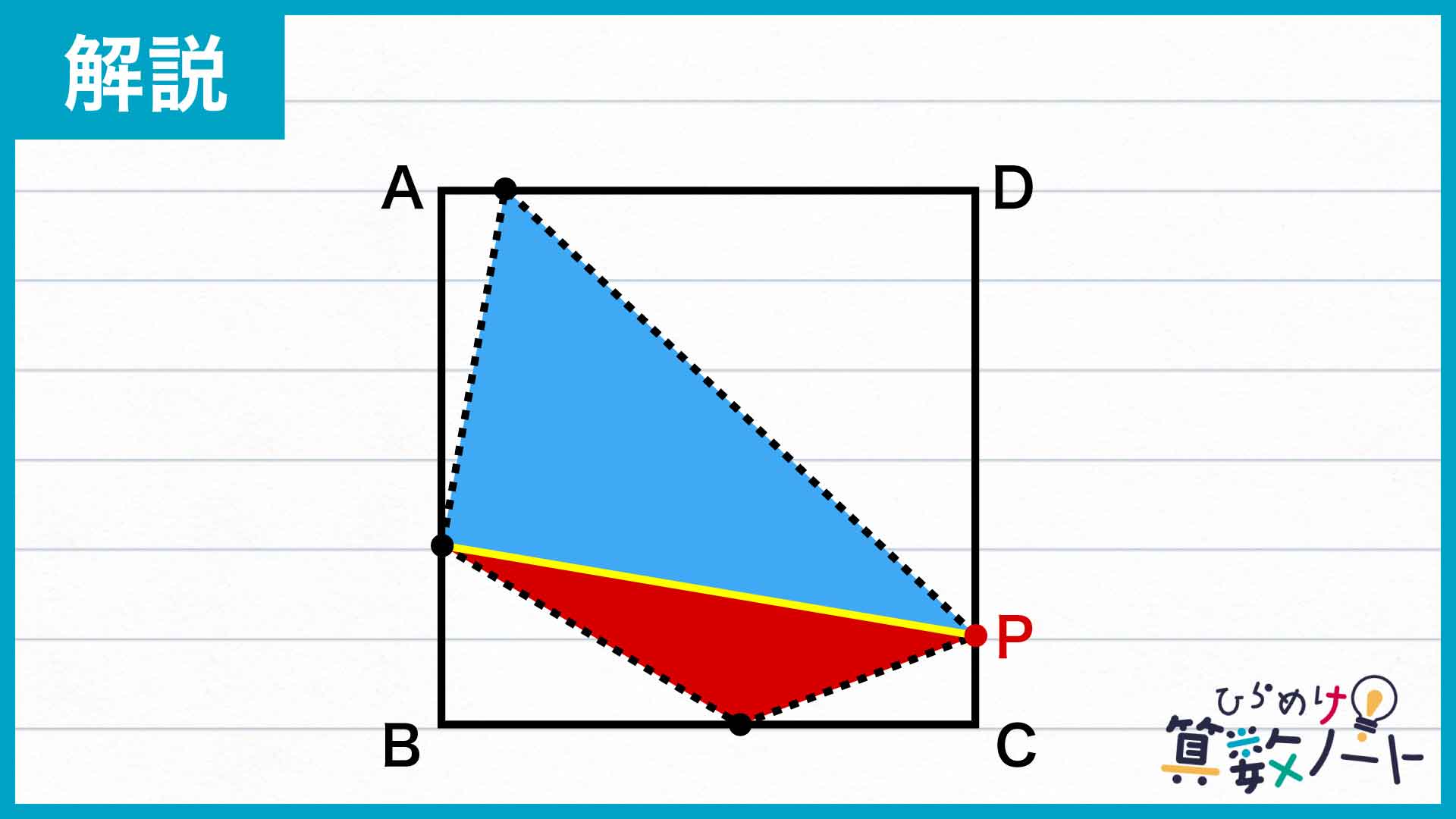
ここで大切なのが、正方形ABCDと、点Pを含む4点で囲まれた四角形を、それぞれ2分割することです。点Pを含む四角形はこのままだと歪んでいて面積を考えづらいので、下の図のように2つの三角形に分けてみましょう。

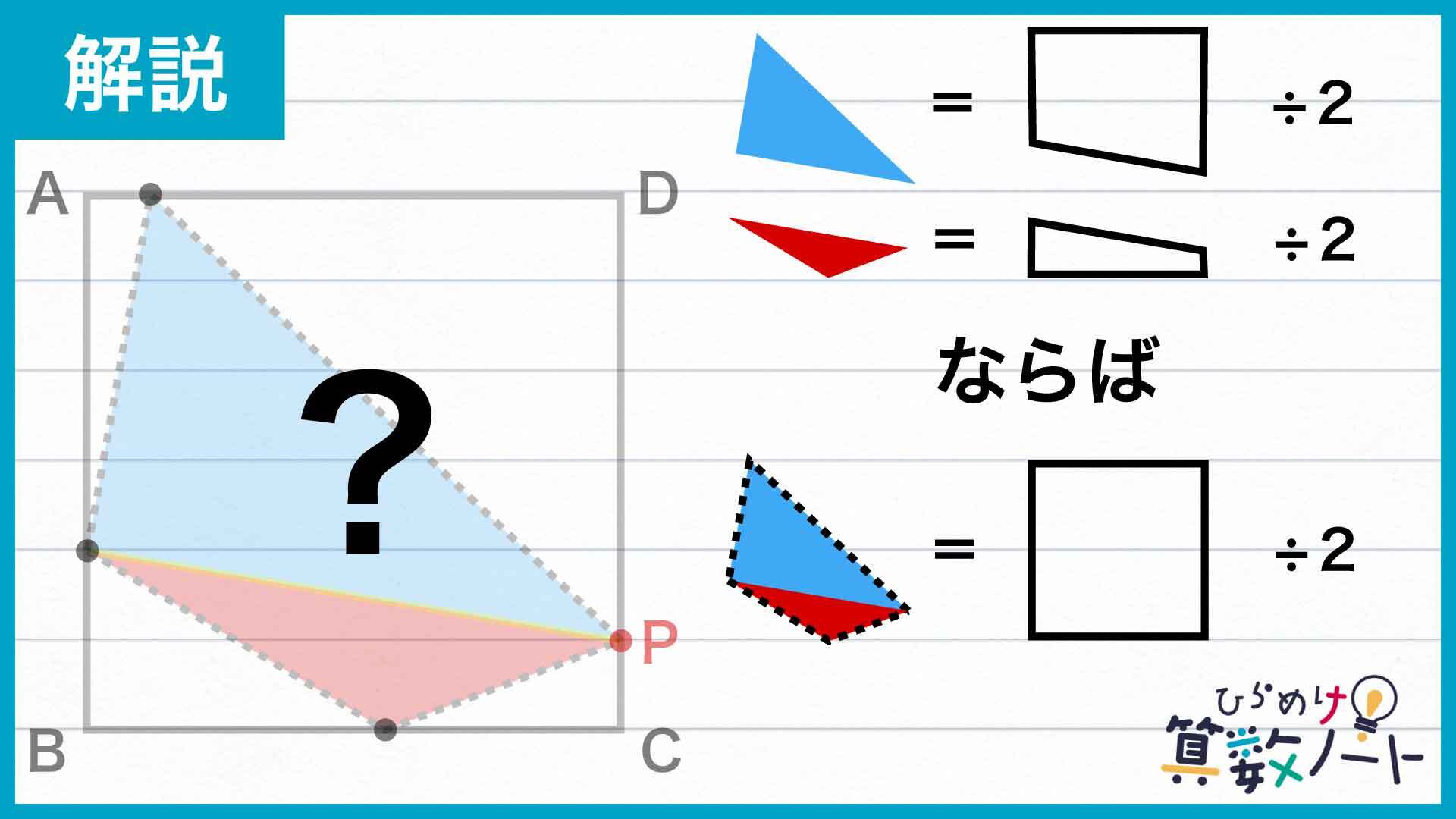
このとき、正方形ABCDも上下2つの四角形に分かれます。もし、塗りつぶされた三角形の面積がそれぞれ上下の四角形の面積の半分になる瞬間があれば、点Pを頂点のひとつとする四角形全体の面積も正方形ABCDの半分ということになります。

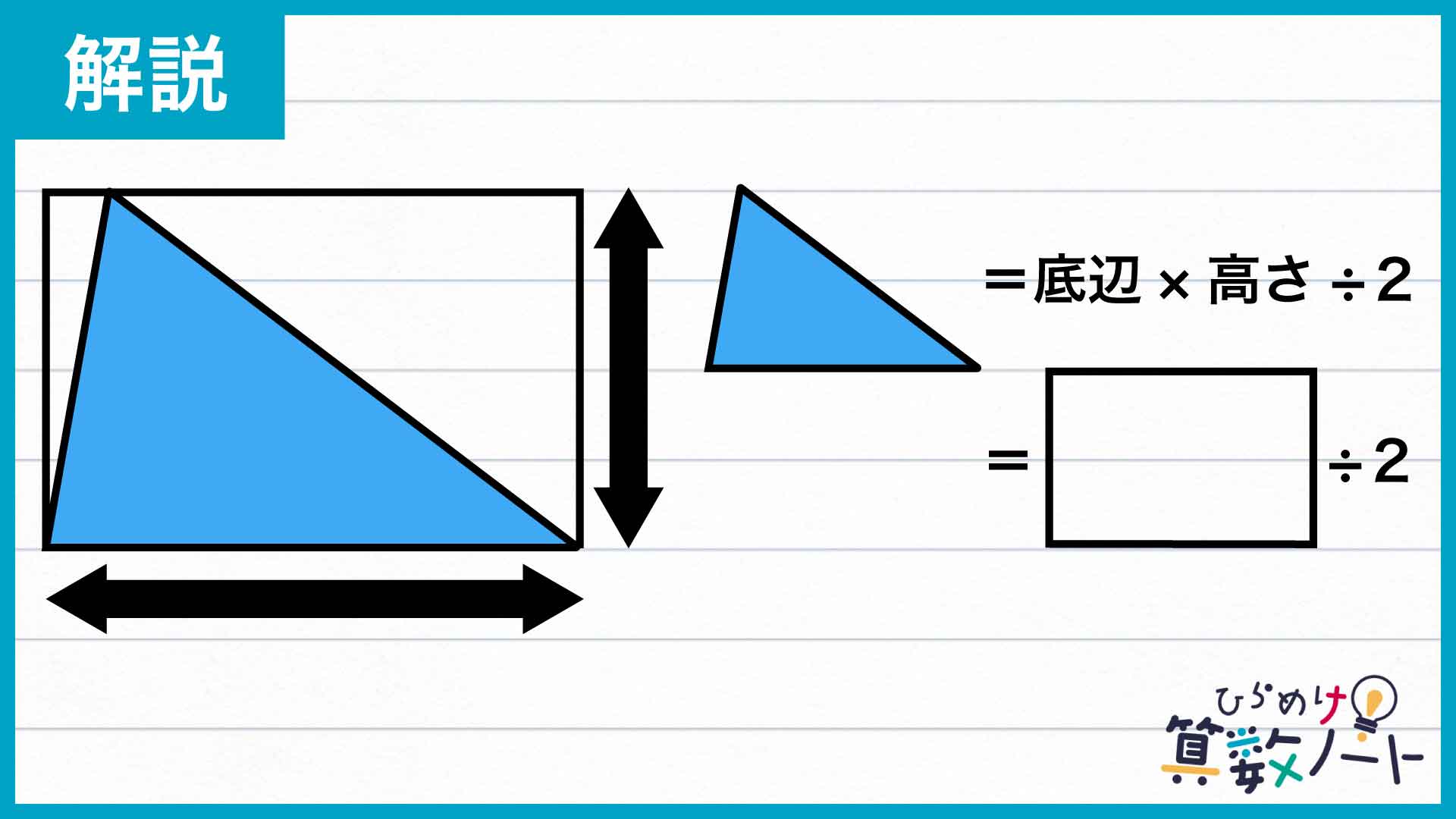
三角形の面積は、「底辺×高さ÷2」で求めることができます。つまり、下の図のように三角形と長方形の底辺・高さが等しくなる場合を考えれば、三角形の面積は長方形の面積のちょうど半分となります。

このことを踏まえて、点Pと向かいの点を結んだ線分が正方形の辺AD、BCと平行になる、つまり正方形ABCDが2つの長方形に分割される場合を考えてみましょう。

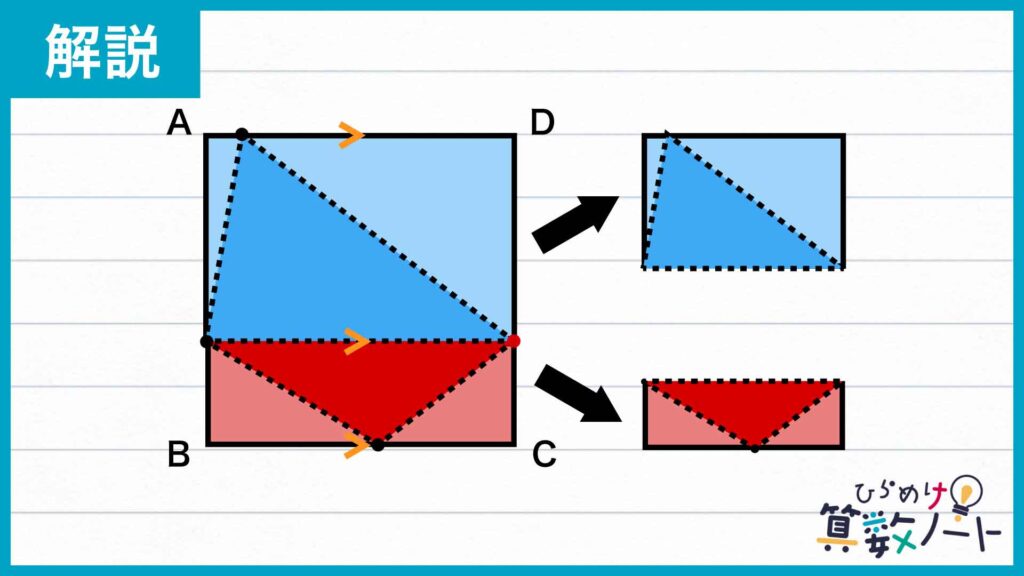
すると、点Pを頂点のひとつとする四角形が分割されてできた三角形2つは、底辺と高さが長方形の辺の長さと一致しており、それぞれの面積は長方形のちょうど半分にあたることがわかります。したがってこのとき、点Pを頂点のひとつとする四角形全体の面積も正方形ABCDの半分になります。

よって、点Pと向かいの点を結んだ線分が正方形の2辺と平行になるとき、つまり点Pが頂点Cを出発して3だけ進んだときが求める瞬間だとわかるのです。

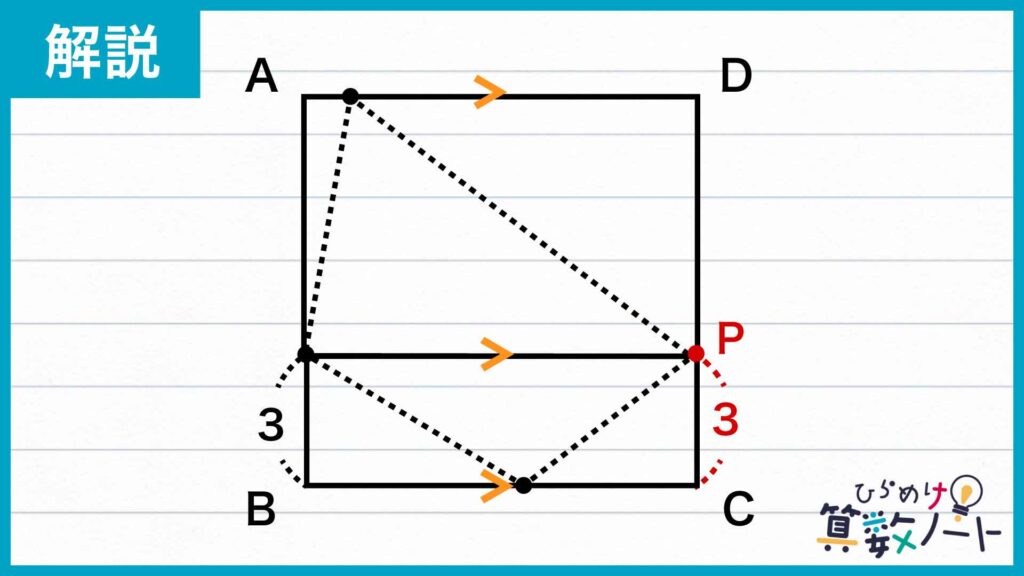
点Pは毎秒1の速さで動くので、求める時刻は3÷1=3秒後となります。

答え：3秒後

ちなみに、出発から3秒後以外に答えになりうるタイミングはないのでしょうか？　実は、赤い四角形を除く「余白」の部分の変化について考えれば、点Pが動くにつれ赤い四角形は大きくなる一方、すなわち条件を満たすタイミングは一度しかないことがわかります。余裕のある方はぜひ、このことについても考えてみてくださいね。

「ひらめけ！算数ノート」のバックナンバーはこちら！

【前回の算数ノートはこちら】

【あわせて読みたい】