ひらめけ!算数ノート p.182小学生でできる「正方形と動く点P」の問題、あなたは解ける?
理系木村 真実子2026.02.04
ヒント
今回の問題は、「四角形の面積が元の正方形の半分になる」状況を思い描けるかが最大のカギ。きちんとイメージできてしまえば、難しい計算はいりません。
四角形同士で面積を比べるとなると複雑ですが、ある長方形や正方形について「面積が半分の三角形」を考えるのは比較的簡単です。三角形の面積は「底辺×高さ÷2」で求められるので、図のように長方形と底辺・高さを共有する三角形なら面積は長方形のちょうど半分になります。
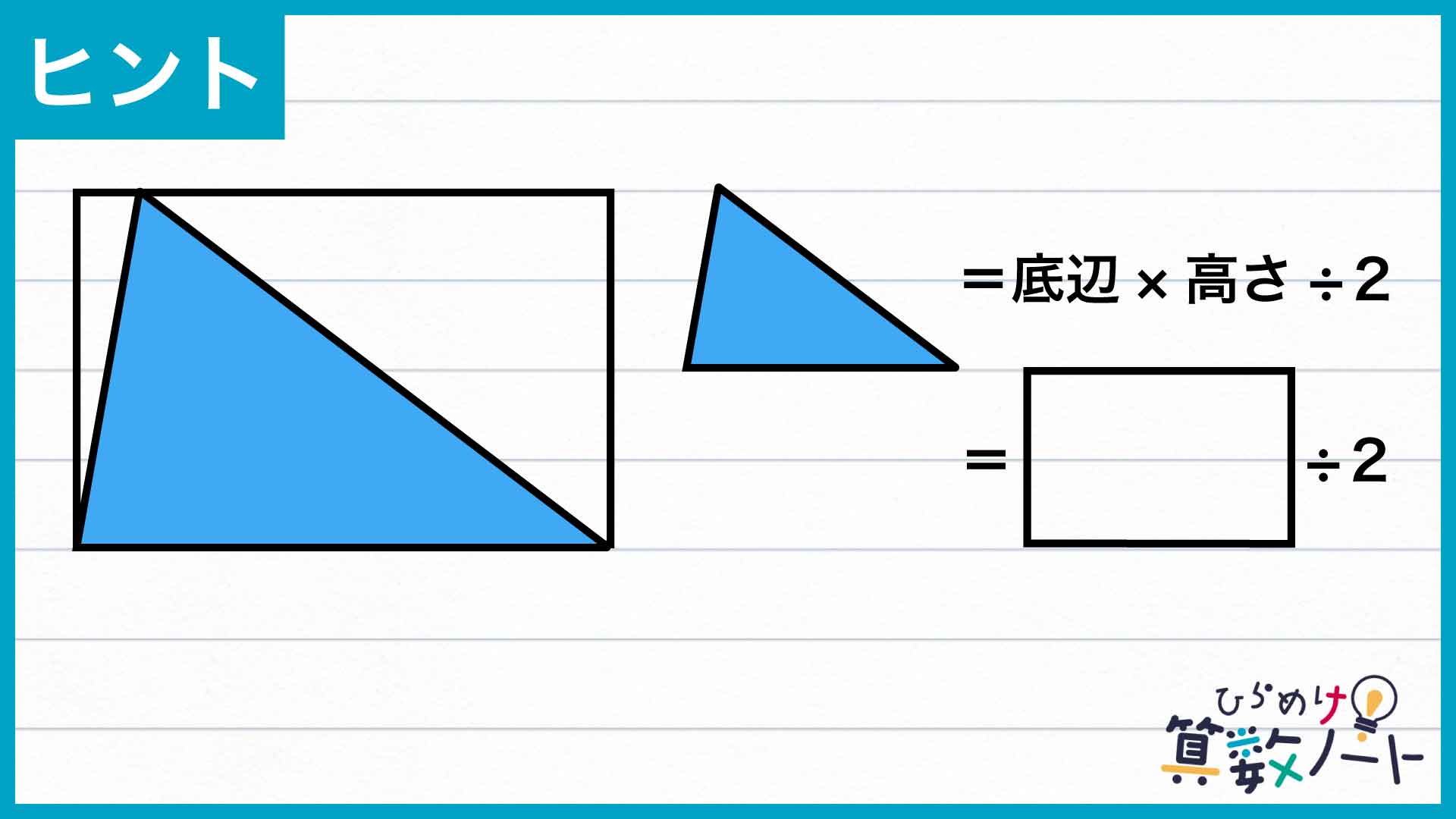
このことを今回の問題に応用してみましょう。正方形ABCDと、点Pを含む4点で囲まれた四角形を、それぞれ2分割して考えてみると……?
今回はあえて、ヒント少なめでいかせていただきます。「面積が半分になる」状況、イメージできましたか?
3ページ:【答え&解説】図形を分割して考えよう! 答えがわからない場合はこちらへ
Amazonのアソシエイトとして、当サイトは適格販売により収入を得ています。
関連記事
この記事を書いた人

木村 真実子
東京大学大学院修士1年の木村です。生物素材化学について勉強しながら、作問したり早押ししたりしてクイズを楽しんでいます。好きなものはJ-POP・広島東洋カープ・フクロウなど。身の回りを見渡すのが少し楽しくなるような記事を目指します。よろしくお願いします。
木村 真実子の記事一覧へ





















.jpg)







