問題はこちら
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
この問題の解き方をまとめた図がこちらです。
大切なのは、AからBを引いた部分を、面積が求められる形で考えることです。
では、このポイントを踏まえつつ解いていきましょう!
扇形の中心角を求める
まず、下の図でA、Bそれぞれの図形を囲んでいる扇形の中心角について考えます。
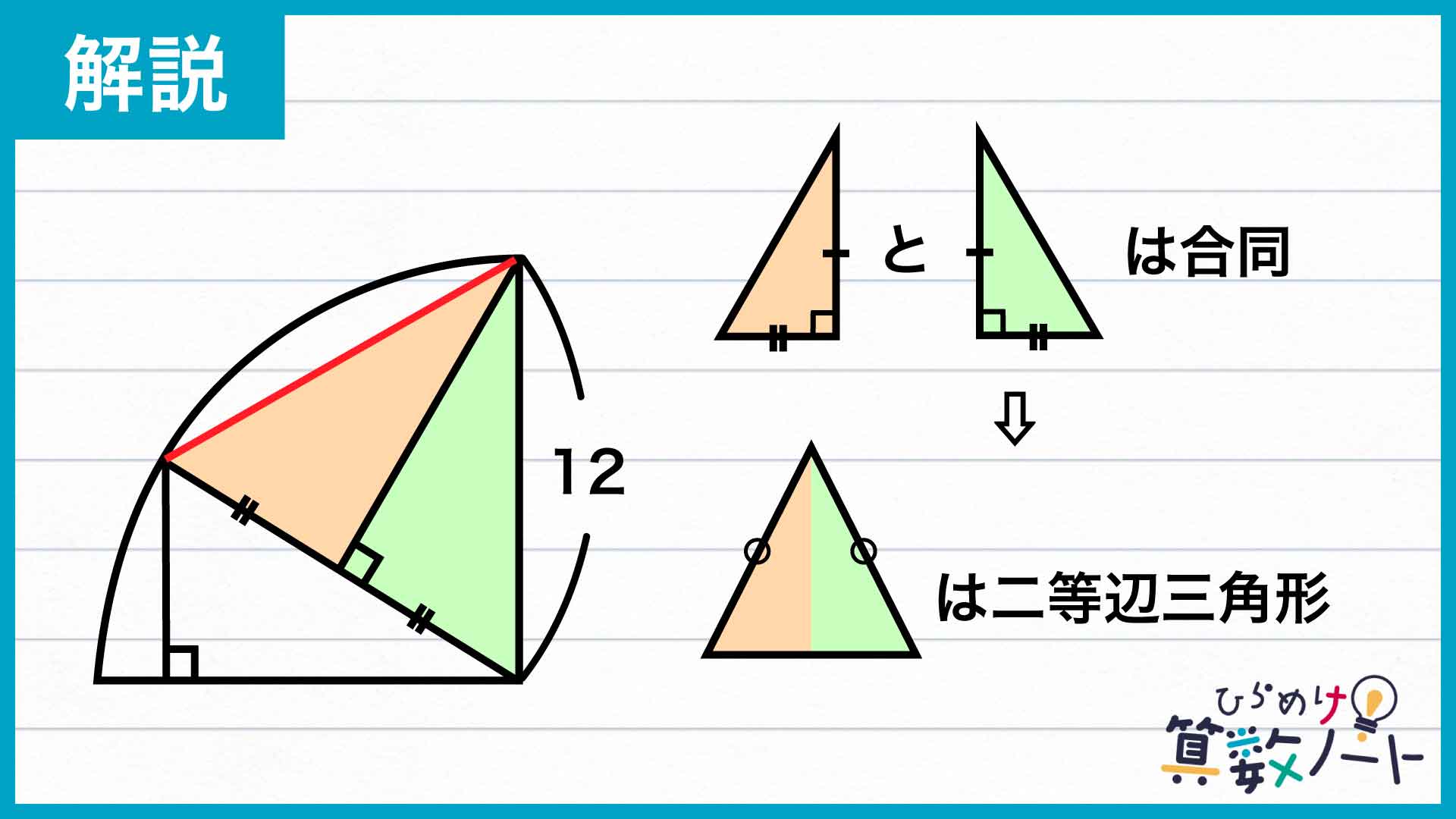
ポイントになるのは、下の図の左側において赤で示された補助線を引くことです。そして、図の右側で色分けされた2つの三角形に注目してみましょう。
2つの三角形はどちらも直角三角形であり、直角を挟む2つの辺のうち一方は共通の辺、もう一方は扇形の半径を2等分したものであることがわかっています。したがって、1つの角とそれを挟む辺の長さが等しいことから、2つは合同な三角形であるといえます。
したがって、残り1つの辺の長さも等しく、2つの三角形を組み合わせてできる大きな三角形は二等辺三角形であるとわかるのです。
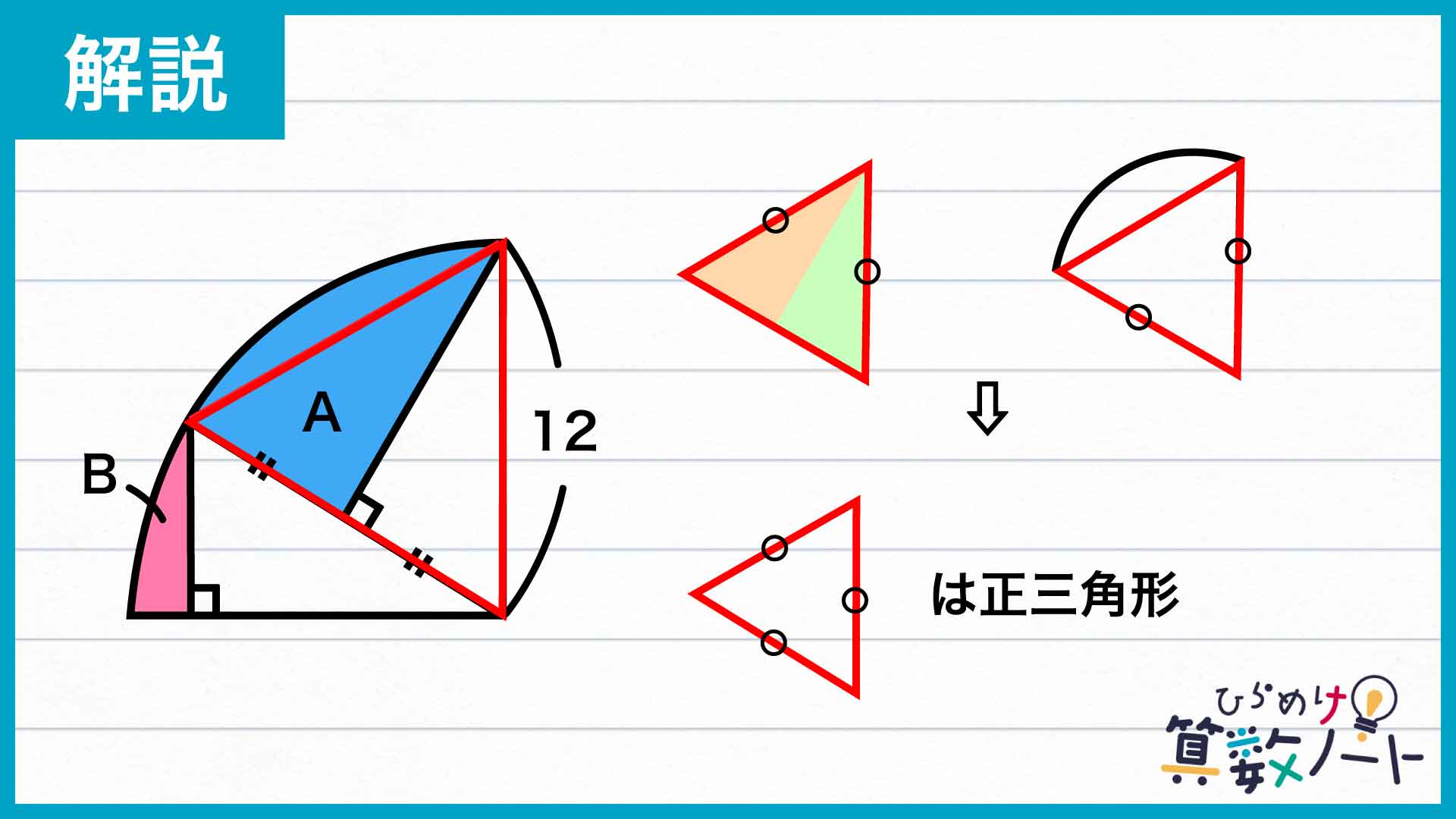
さらに、この三角形では、同じ扇形の半径にあたる2辺の長さも等しくなっています。以上のことから、この三角形は3辺の長さが全て等しい正三角形であることがわかるのです。
このことから、A、Bそれぞれの図形を囲んでいる扇形の中心角がわかります。Aを囲む扇形の中心角は正三角形の内角と同じ60度、Bを囲む扇形の中心角は90-60=30度と求めることができるのです。
A、Bを「図形の引き算」で考える
A、Bそれぞれの面積を直接求めることは難しいため、簡単な図形同士の「引き算」で考えることがポイントです。
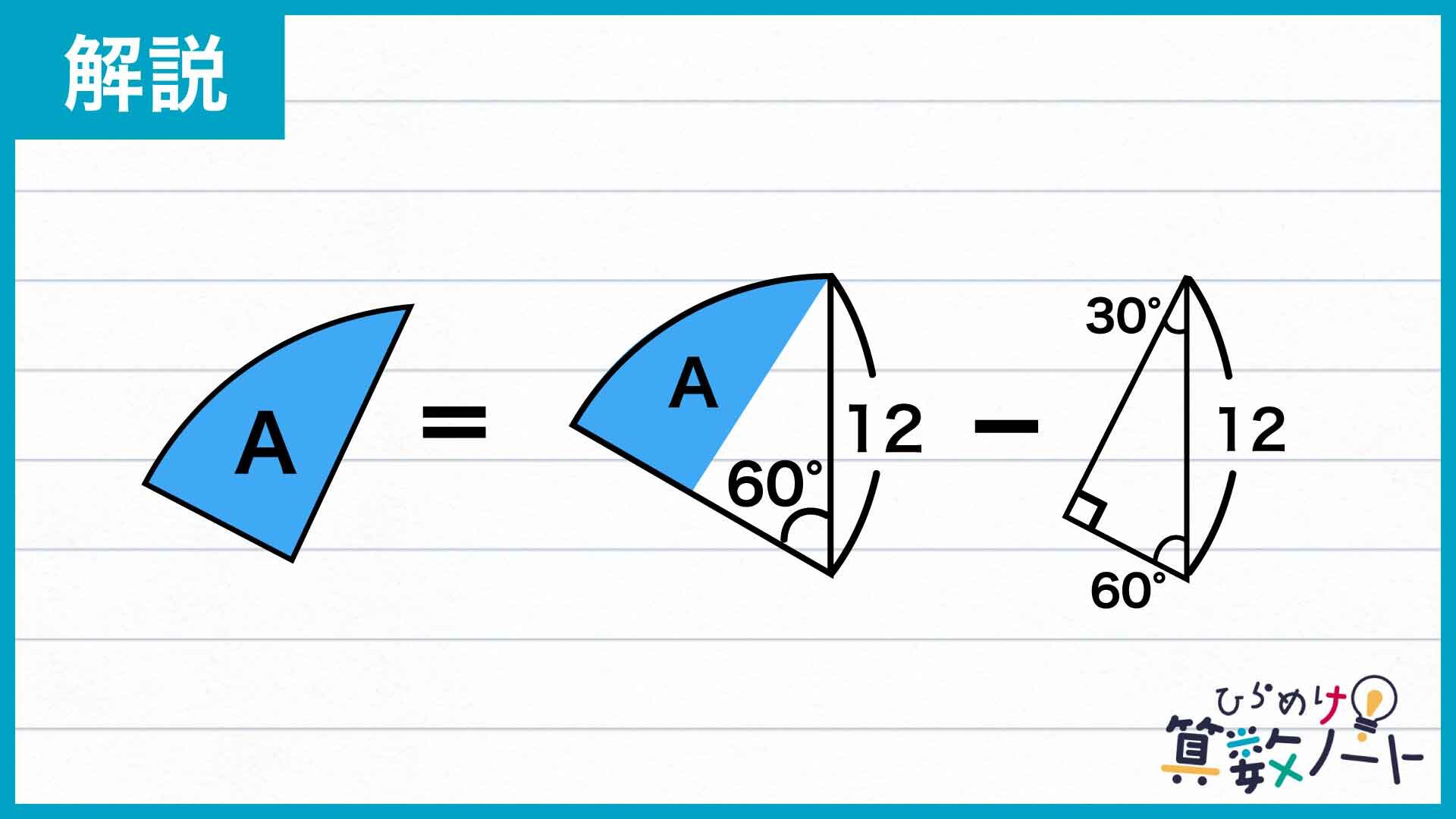
まずAは、中心角60度の扇形から直角三角形を引いた部分にあたります。この直角三角形は正三角形をちょうど半分にした図形であり、内角の大きさがそれぞれ90度、60度、30度で、斜辺の長さは12です。
一方Bは、中心角30度の扇形から直角三角形を引いた部分にあたります。この直角三角形も内角の大きさがそれぞれ90度、60度、30度で斜辺の長さは扇形の半径にあたる12、すなわち先ほどの直角三角形と合同な図形といえます。
さらに、中心角30度の扇形は、同じ半径で中心角60度の扇形から中心角30度の扇形を引いた図形であるといえるので、Bの部分については下のように表すことができます。
以上のことから、Aの面積からBの面積を引いた差はちょうど中心角30度、半径12の扇形の面積に等しくなることがわかるのです。
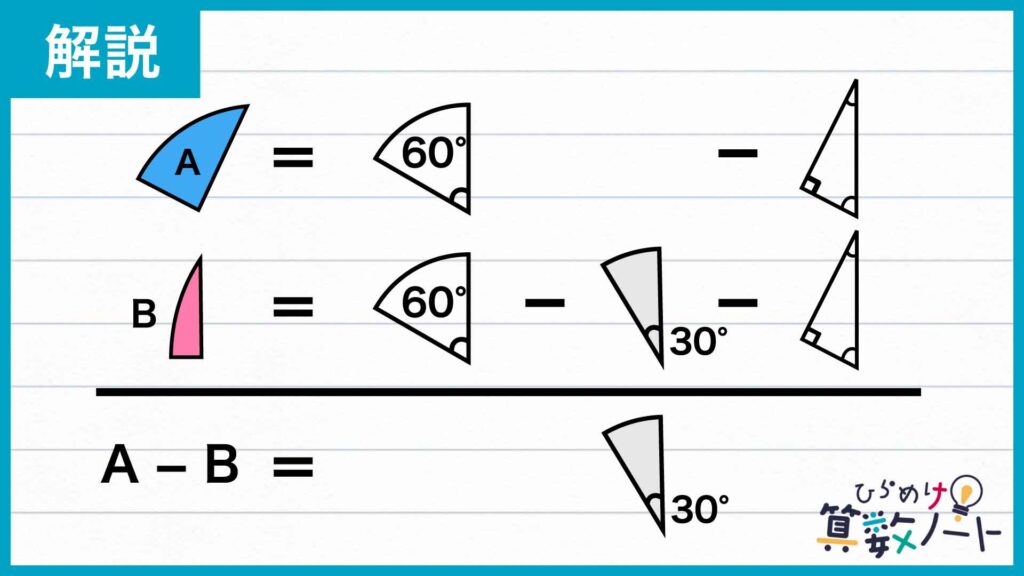
中心角30度の扇形の面積は、同じ半径を持つ円の面積を360÷30=12等分したものに等しくなります。したがって、Aの面積とBの面積の差は12×12×π÷12=12πとなります。
答え:12π
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】














.jpg)









.jpg)







