小学生でも解ける！辺を三等分してできた図形の面積、あなたはわかる？

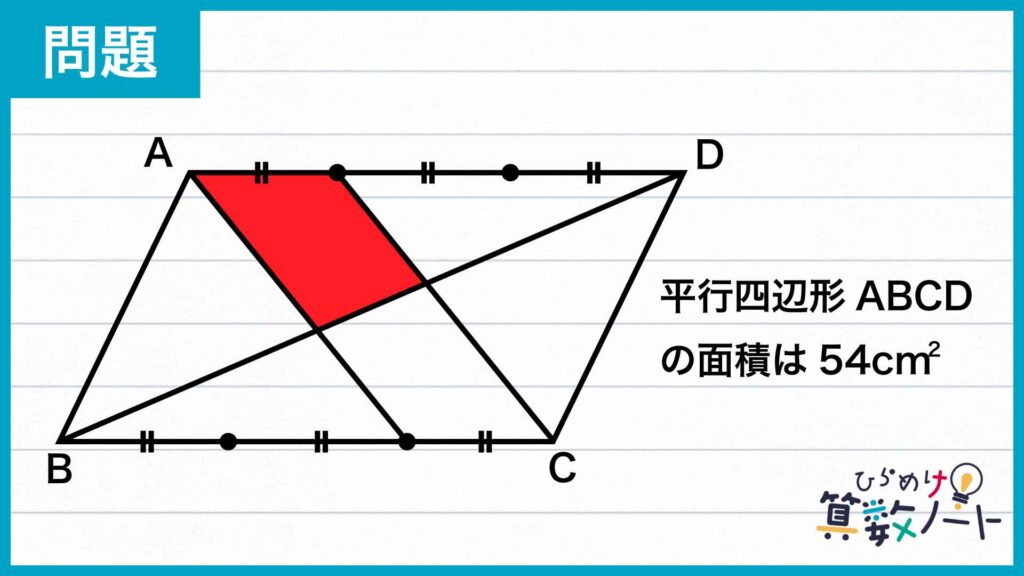
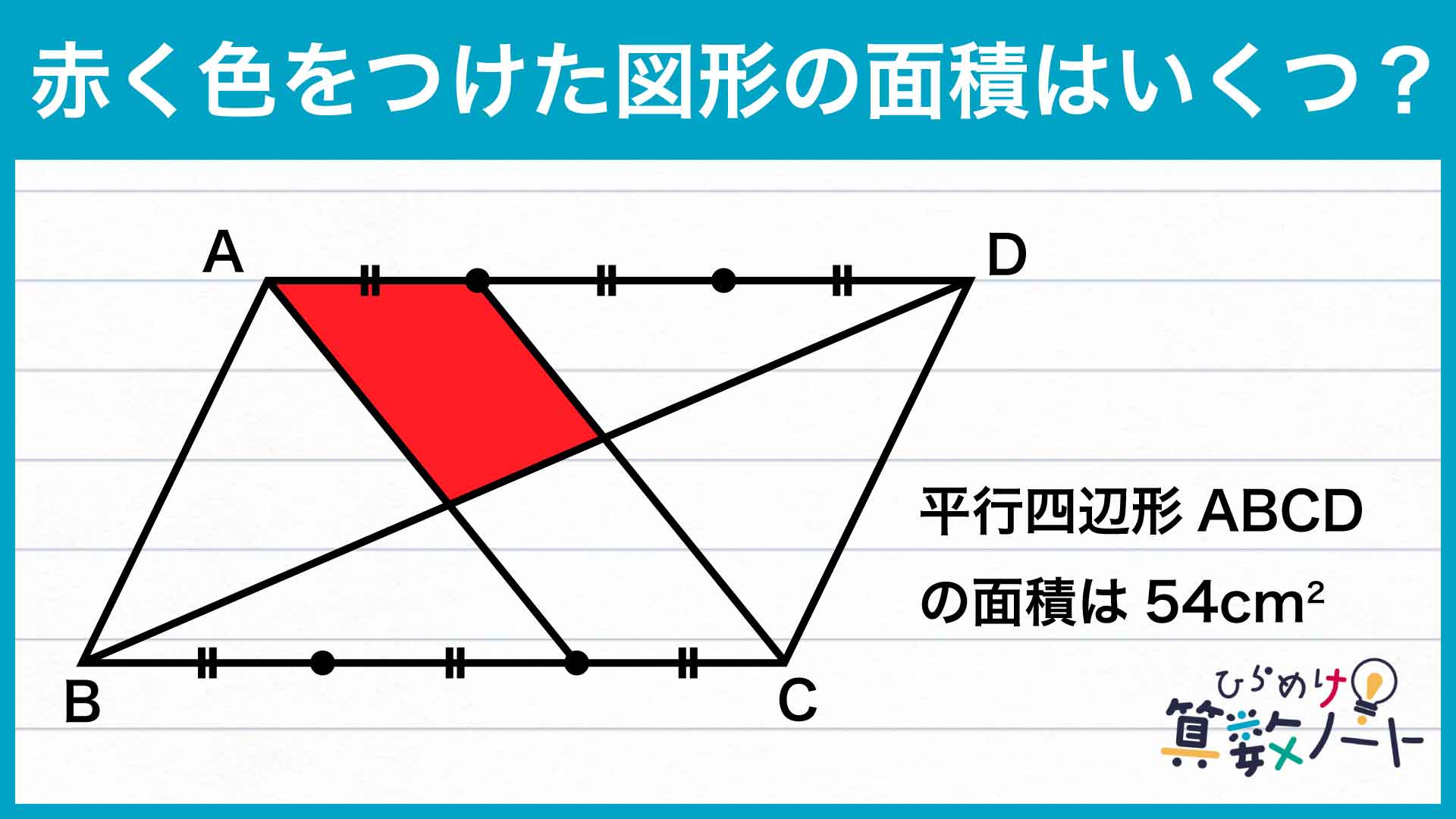
問題はこちら

1ページ：【解答フォーム】自力で解きたい方はこちらへ！以下は問題の解説です

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

この問題の解き方をまとめた図がこちらです。

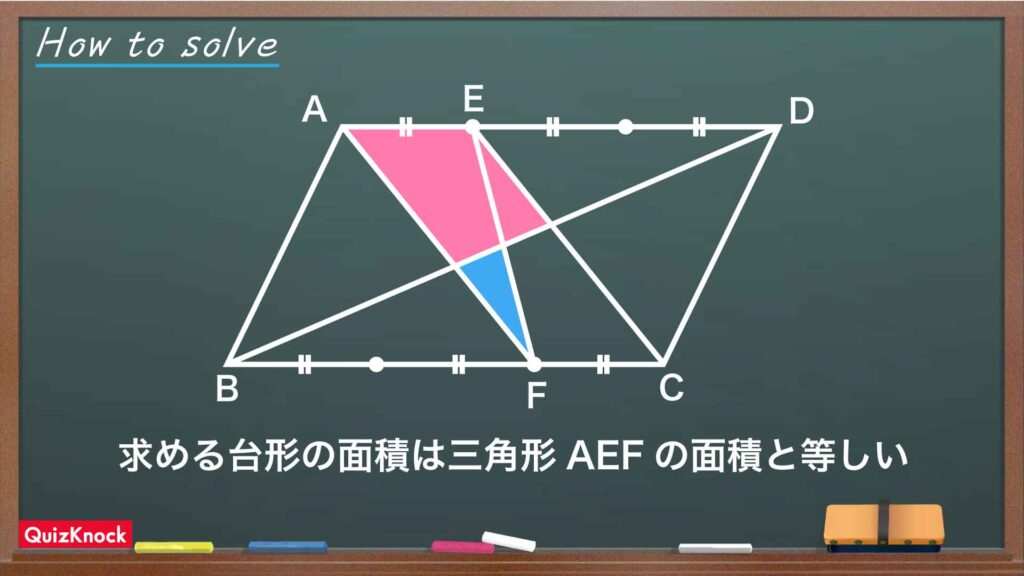
今回のポイントは「平行四辺形を使って面積を求めること」です。

このポイントをもとに、問題を攻略していきましょう！

点E、Fを置いて平行四辺形に注目する

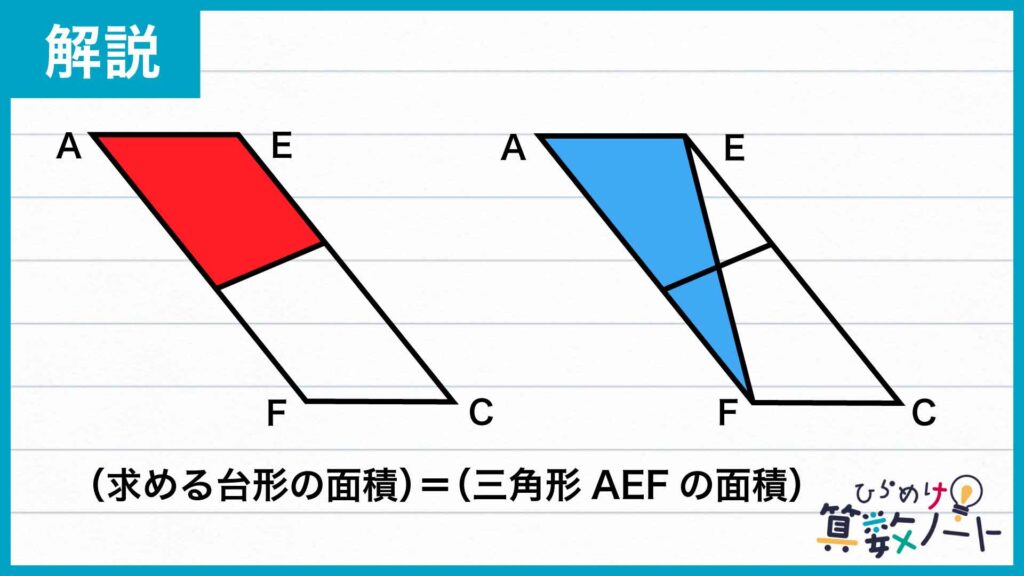
上の図のように点E、Fを配置すると、求める台形の面積は平行四辺形AFCEの面積の半分になります。また、三角形AEFに着目すると、こちらも面積は平行四辺形AFCEの面積の半分です。つまり、求めたい台形の面積は、三角形AEFの面積に等しいことがわかります。

三角形AEFの面積を求める

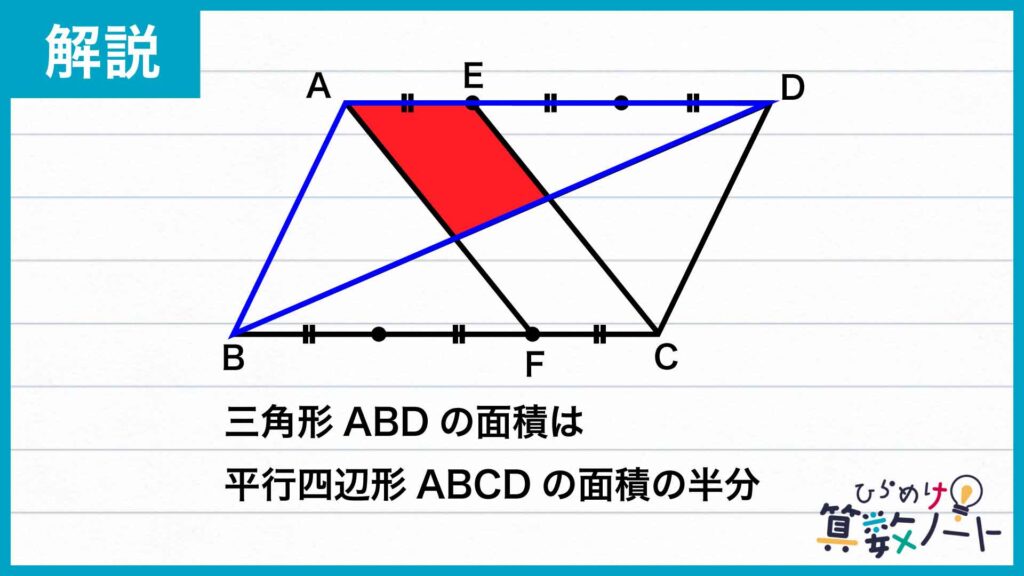
三角形AEFの面積を求めるために、三角形ABDの面積を考えてみましょう。三角形ABDは平行四辺形ABCDの半分の面積です。

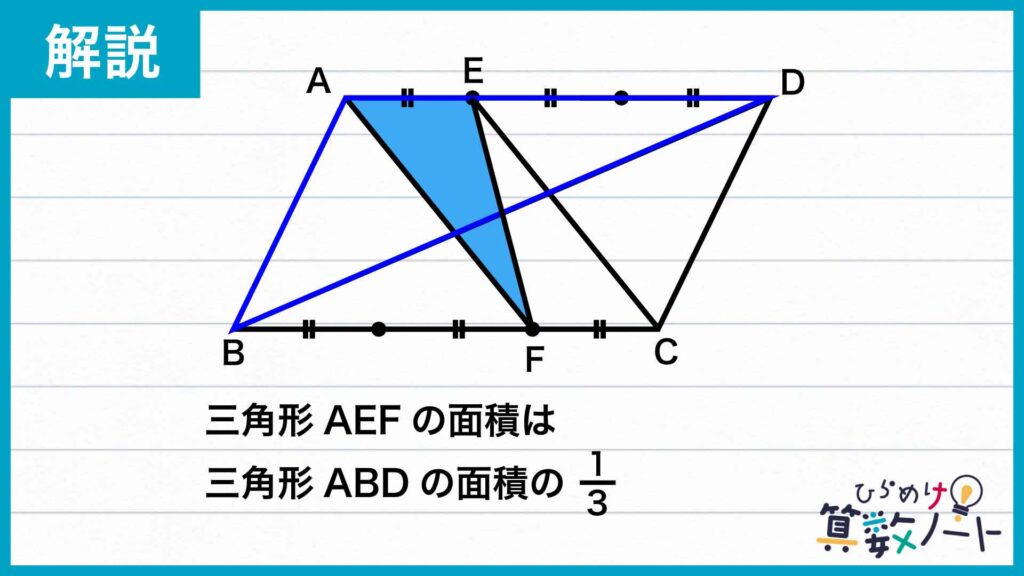
この2つの三角形は、それぞれ辺AD、辺AEを底辺としたときに高さが等しく、AEの長さはADの長さの1/3なので、三角形AEFは三角形ABDの1/3の面積になります。

したがって、（三角形AEFの面積）=54×1/2×1/3=9cm²となります。先ほど示したように、求めたい台形の面積は三角形AEFの面積と等しかったので、これが答えになります。

答え：9cm²

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】