コジマです。
「この回20点取れ!」。ある阪神ファンが大量ビハインドの際(※)に掲げたメッセージである。
※2015年6月13日のオリックス戦(オリックス15-1阪神)
気持ちは大変理解できるものの、20点はいくらなんでも無茶振りである。日本プロ野球における1イニング間の最多得点記録は15点(2009年6月11日、ロッテが対カープ戦で6回裏に記録)で、メジャーリーグでも戦後に限ると17点が最多だというから、プロリーグで1イニング20点は前例がない。
そこで、「この回20点取れ!」る確率を計算してみたところ……何と2億4000万分の1と出た!
前例がない現象の確率を求める方法
1イニング20点は前例がない現象なので、普通に(現象が起きた回数)÷(試行回数)で求めると確率0で終わってしまう。
それでは面白くないので、このように考えることにする。
過去の試合から、0点で終わったイニングは◯◯回、1点で終わったイニングは△△回……と数えてグラフにする。すると、点が多いほど回数が少ない、いわゆる右肩下がりのグラフができあがると考えられる。
当然20点のところは0回だが、グラフを20点のところまで伸ばすことで(このように既存のデータにない値を推定することを
今回はこの方法で求めることにした。
過去3年分、0得点の回がほとんど
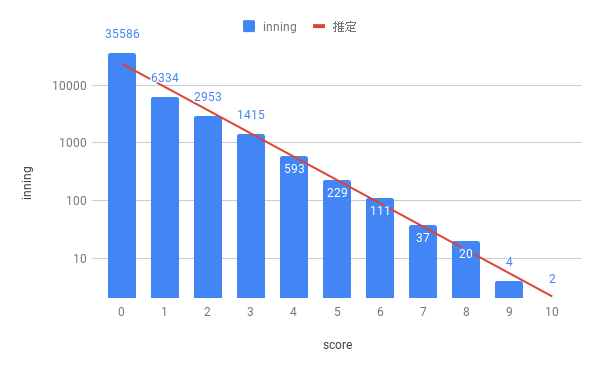
イニング毎得点のデータは日本プロ野球記録というサイトに集計されているものを利用させていただいた。3シーズン(2016年〜2018年)の交流戦を含めた両リーグの全2,574試合から、47,284イニングの得点を集計した結果はこちら。
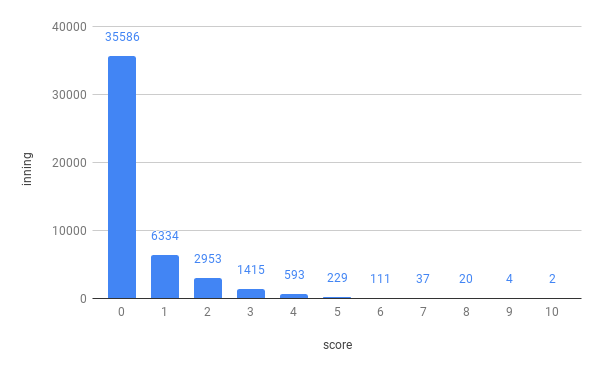
0得点の回が大半で、得点数が増えると回数が減る予想通りのグラフになった。過去3シーズンで生じたビッグイニングは10得点が最多で、11得点以上はなかった(2019年4月10日の広島-ヤクルト戦で、ヤクルトが延長10回表に12得点を達成しているが、今回の分析では含めていない)。
このグラフを元に、20点の回が生じる確率を求めてみる。
2億4000万の分母
減少の仕方が指数関数的(横軸が1目盛り増えると縦軸がr倍になる)なので、縦軸を対数目盛(縦軸が1目盛りにつき10倍になる目盛り)にしてみよう。
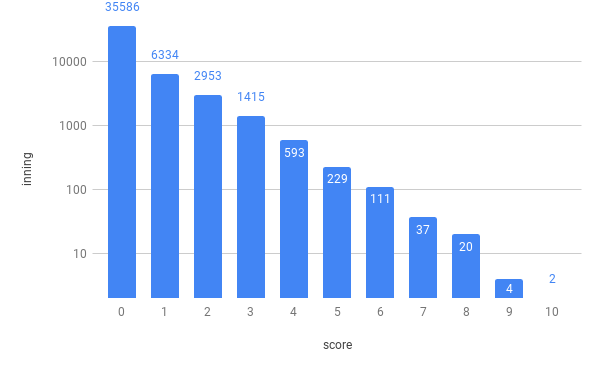
何となく直線が引けそうな感じになったので、最小二乗法で傾きとy切片を求め、推定値のグラフを描いてみた。結構いい線をいっている。
なお、似たようなことをシンデレラガール総選挙を分析する記事でやっているので、より詳しく知りたい方は読んでほしい。
推定式を用いて、20点入るイニングが生じる確率を求めてみると……0.00000000418。分数で表すと2億4000万分の1だ。
1シーズンにだいたい16,000イニング消化されるとして、2億4000万イニングは15,000シーズン分。我々が生きているうちに「20点取れ!」が報われるイニングは訪れなさそうだ……。











.jpg)