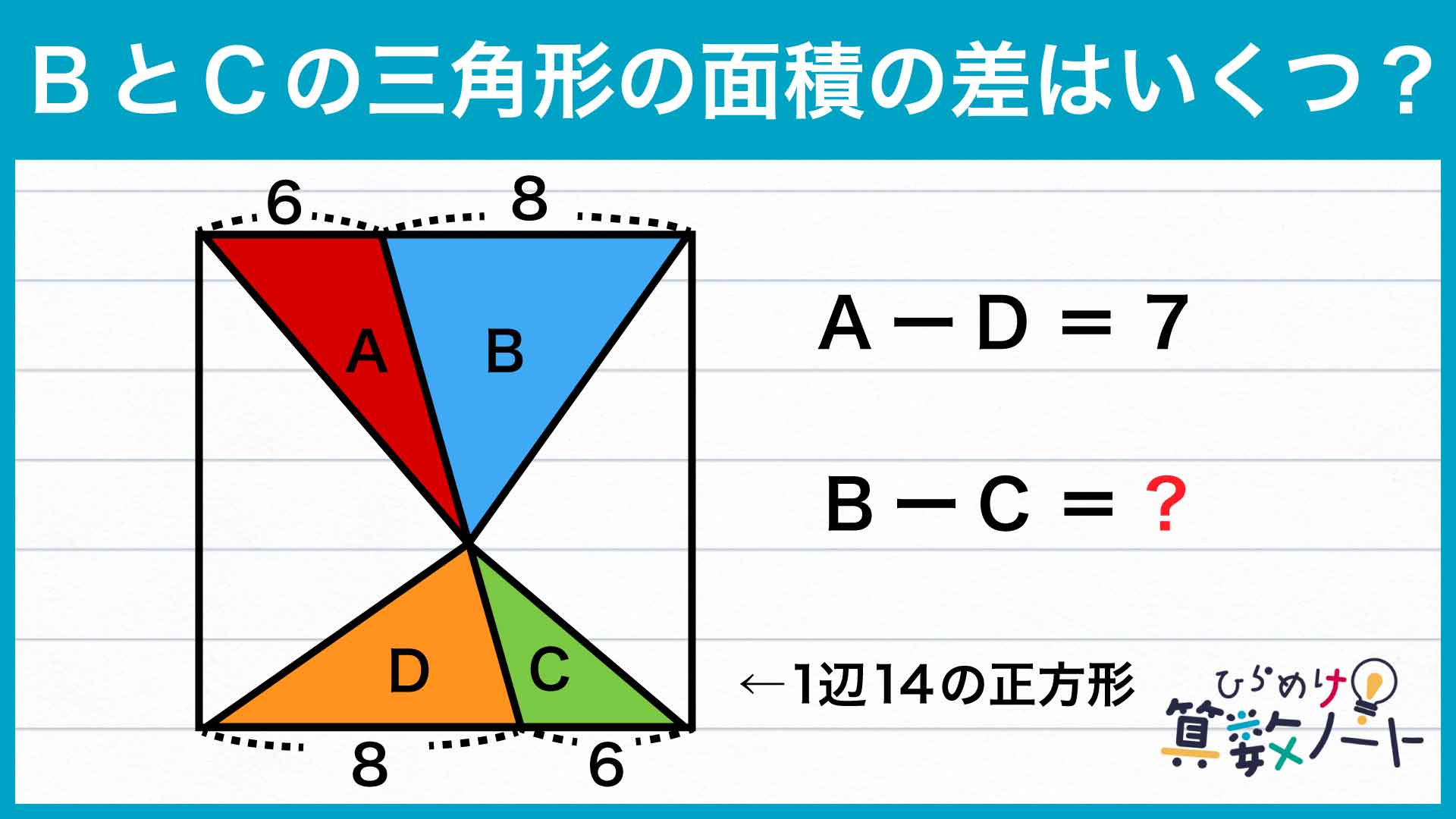
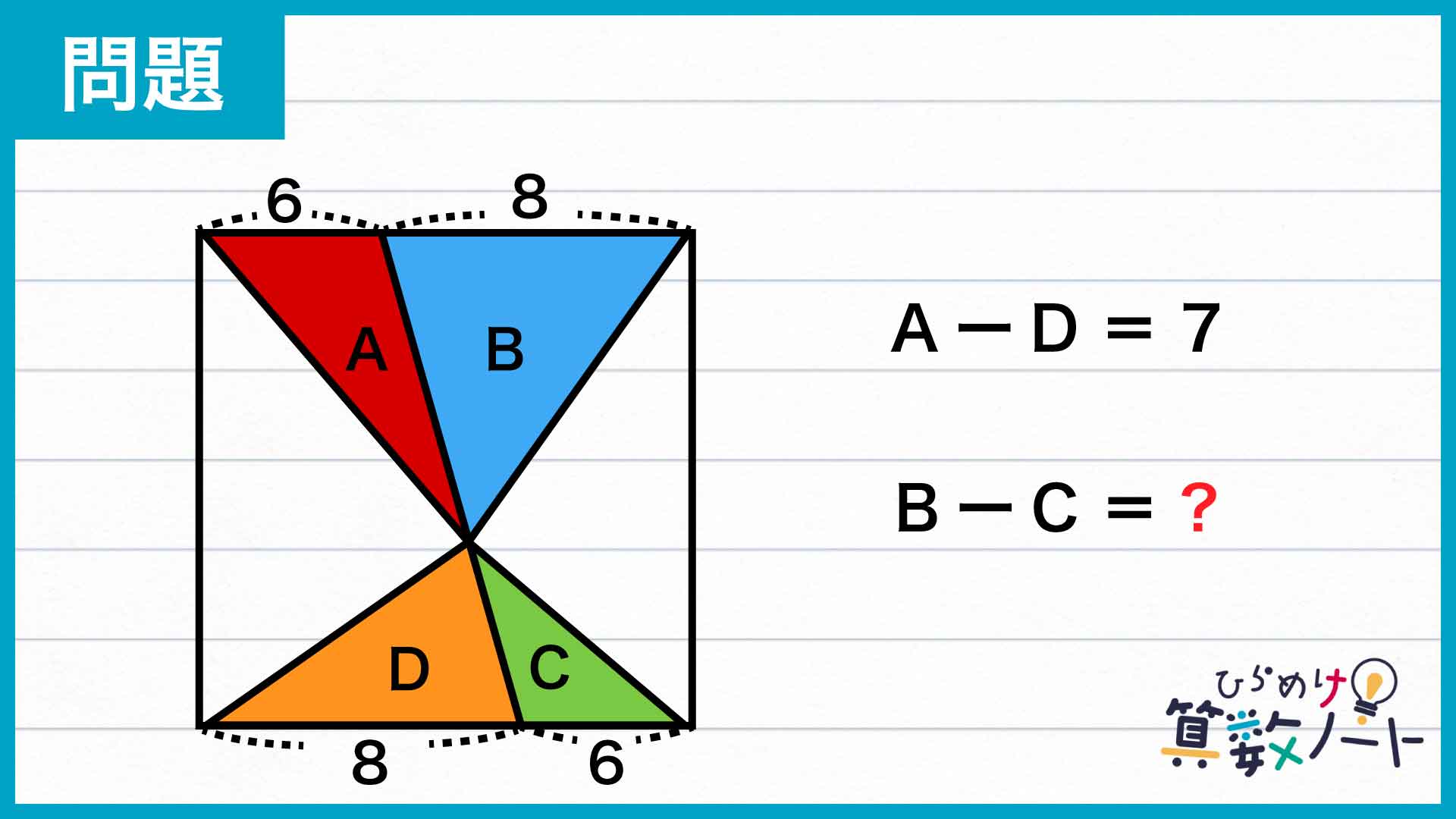
問題はこちら
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
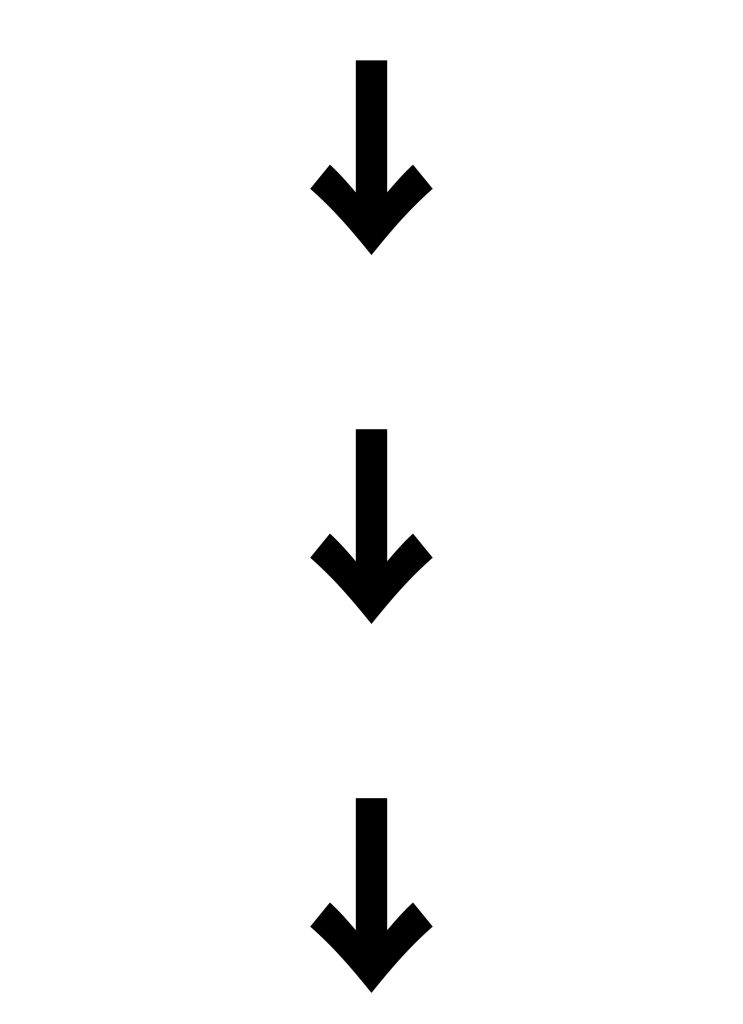
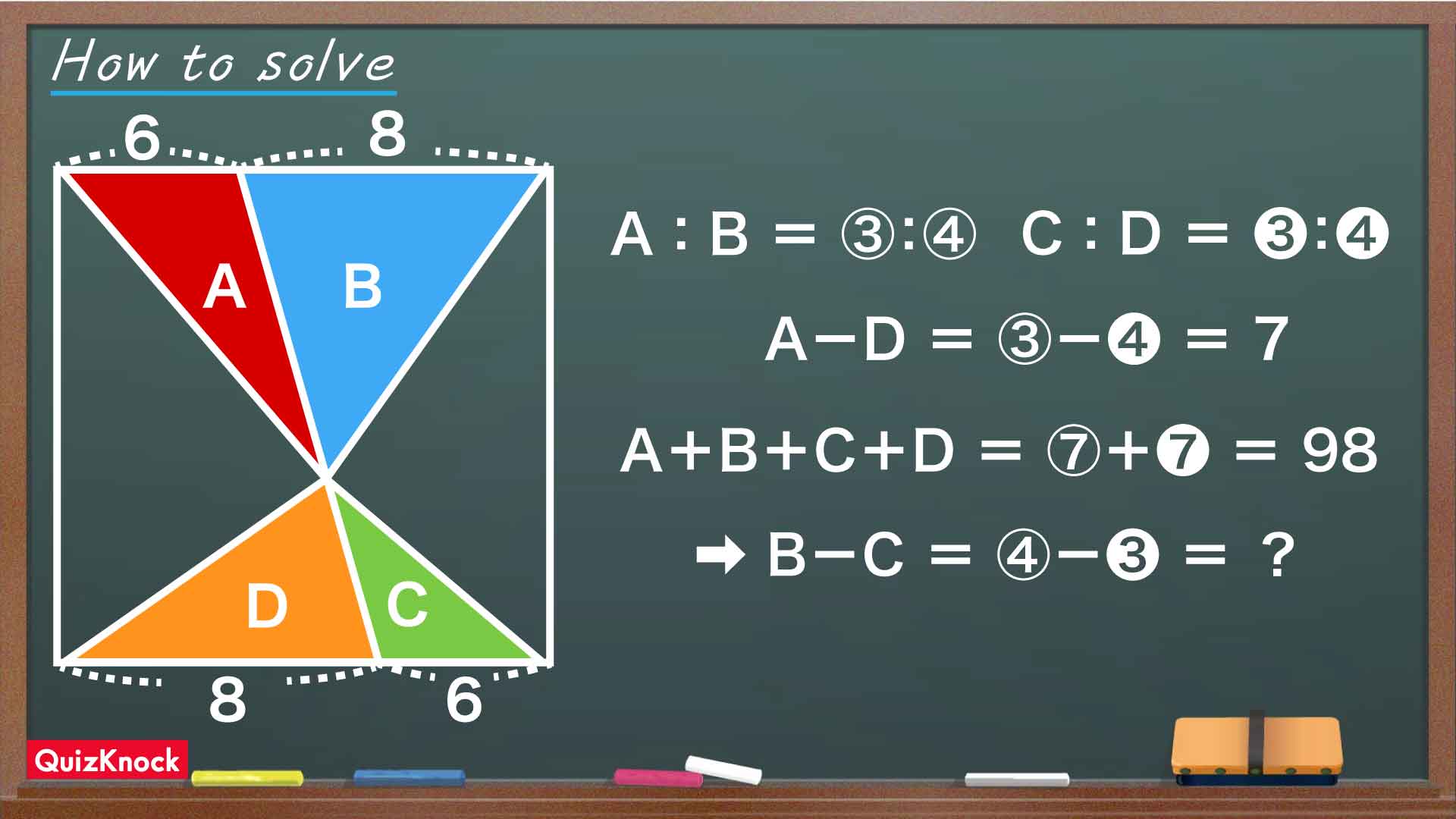
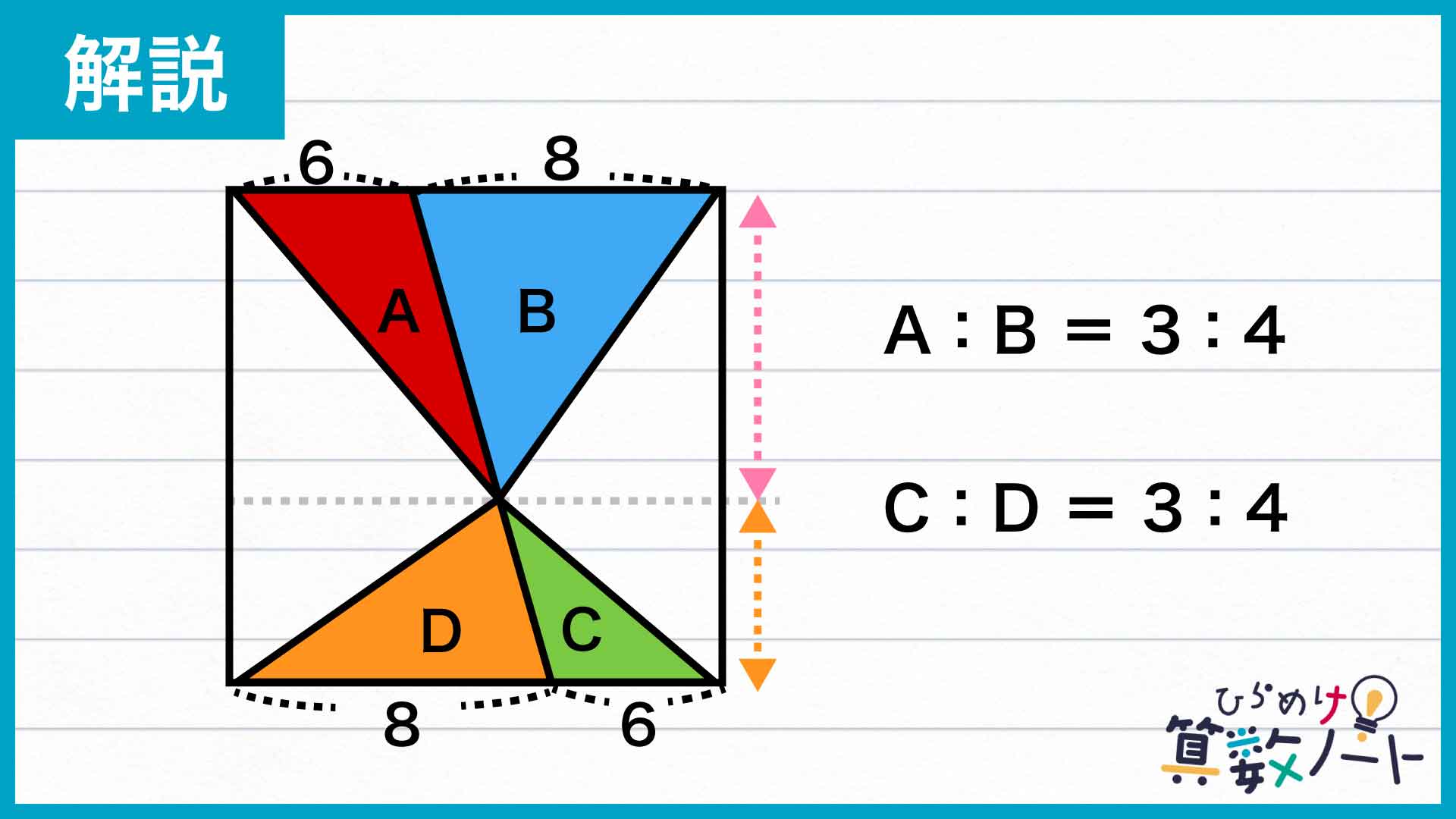
この問題の解き方をまとめた図がこちらです。
大切なのは、2組の三角形の面積比を用いて情報を整理することです。
では、このポイントを踏まえつつ解いていきましょう!
三角形の面積比を考える
まずポイントになるのは、「高さの等しい三角形の面積比は底辺の長さの比に等しくなる」ということです。このことから、高さが共通している三角形AとB、CとDについてそれぞれ面積比がわかります。底辺の長さから、2組の三角形の面積比についてA:B=C:D=6:8=3:4が成り立ちます。
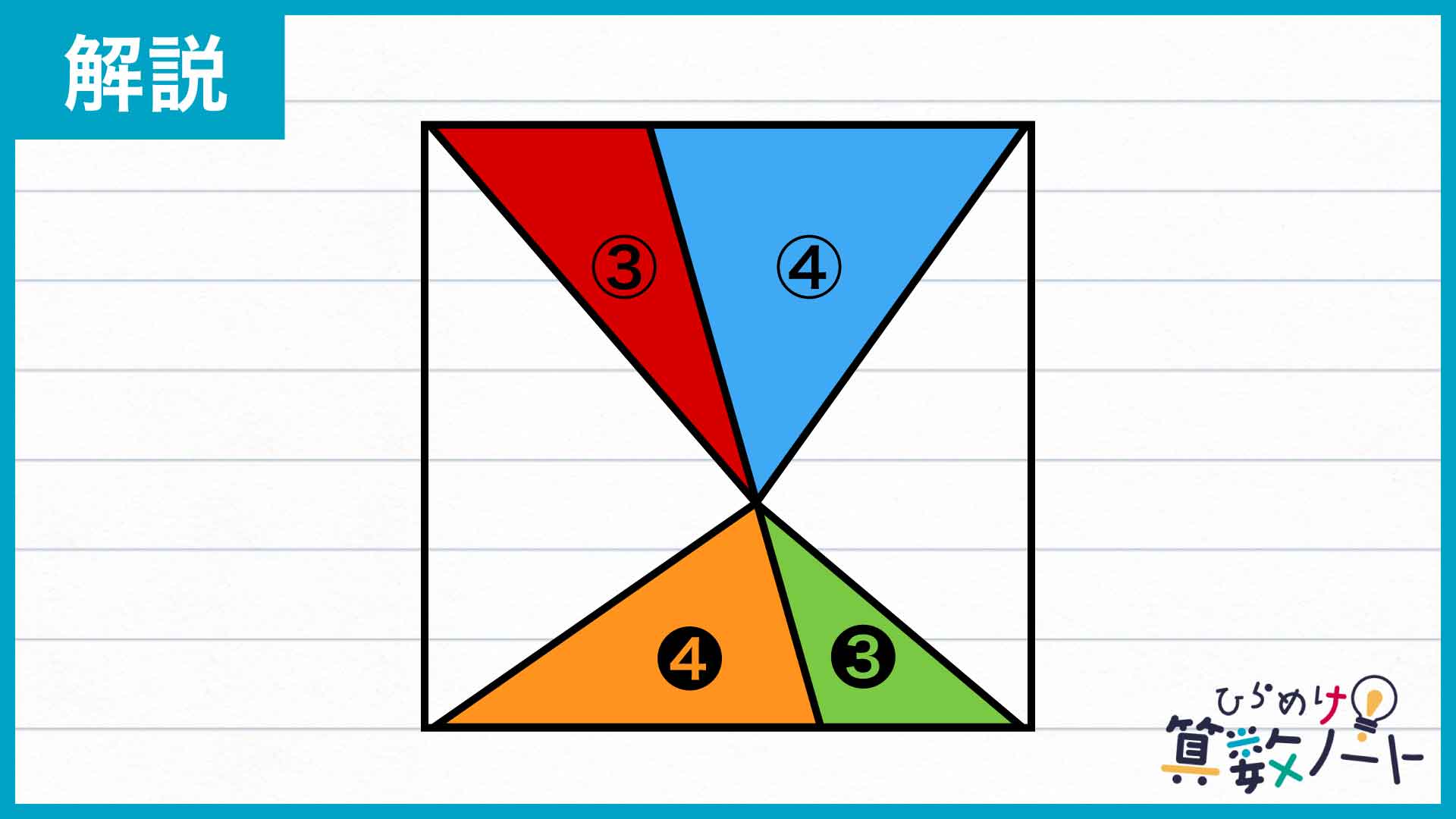
そこで、4つの三角形の面積をそれぞれA=③、B=④、C=❸、D=❹と表してみます。③と❸では実際の面積が異なることに注意してください。
面積の関係を整理する
問題文に「Aの面積がDの面積より7大きい」とあるので、A-D=③-❹=7が成り立ちます。
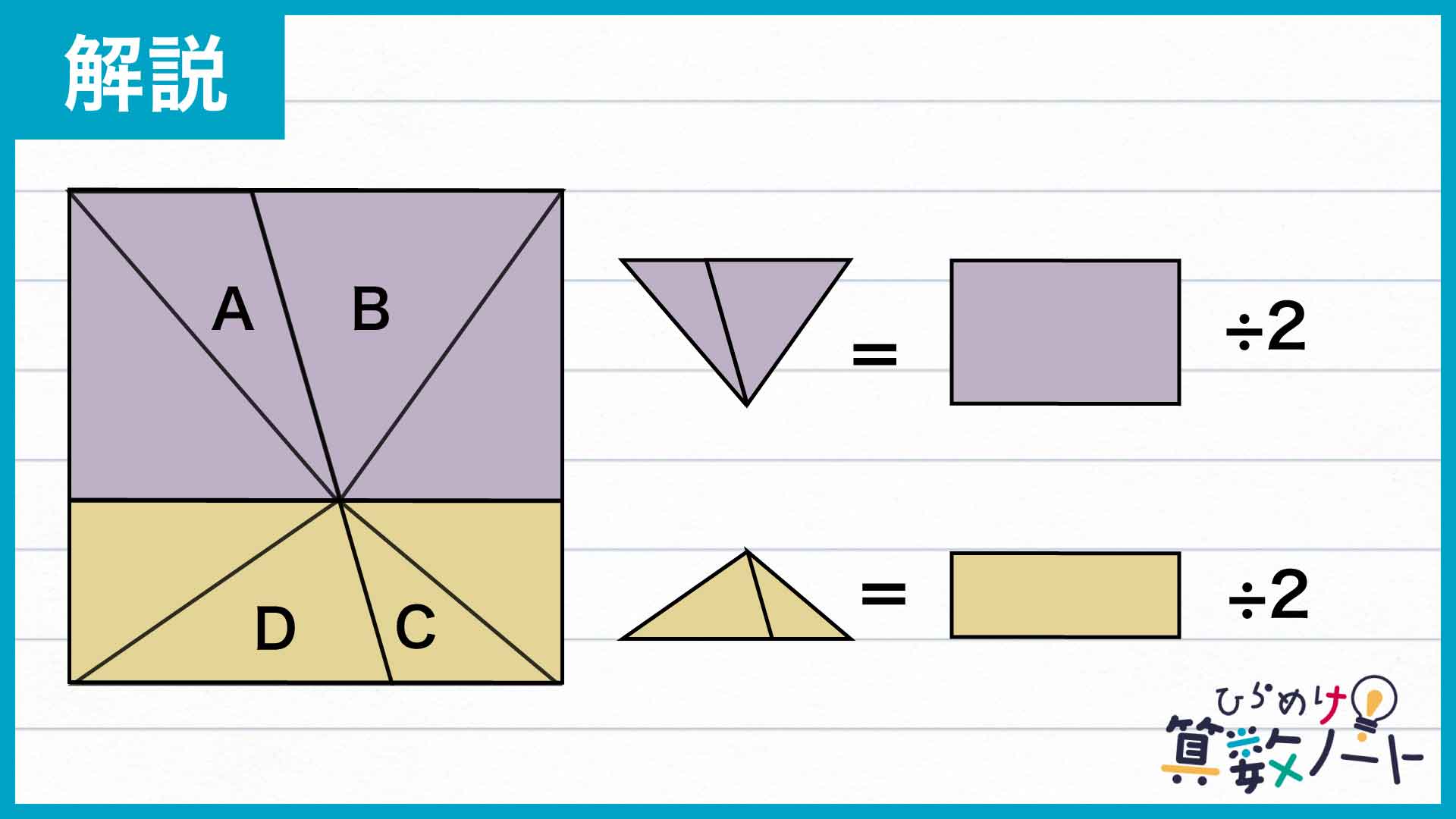
さらに、正方形を上下2つの長方形に分けてみるとAとBの面積の合計、CとDの面積の合計がそれぞれ紫色と黄色で示した長方形の面積の半分にあたります。
したがって、4つの三角形の面積の合計A+B+C+D=③+④+❸+❹=⑦+❼は、1辺が14の正方形の面積のちょうど半分にあたります。よって⑦+❼=14×14÷2=98が成り立ち、左辺・右辺両方を7で割ることで①+❶=14となります。
これまでの過程で、③-❹=7、①+❶=14という2つの式を導くことができました。ここから④-❸の形を作るには、2つの式の左辺をそのまま足せばいいのです。
したがって、Bの面積とCの面積の差は④-❸=21となります。
答え:21
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】









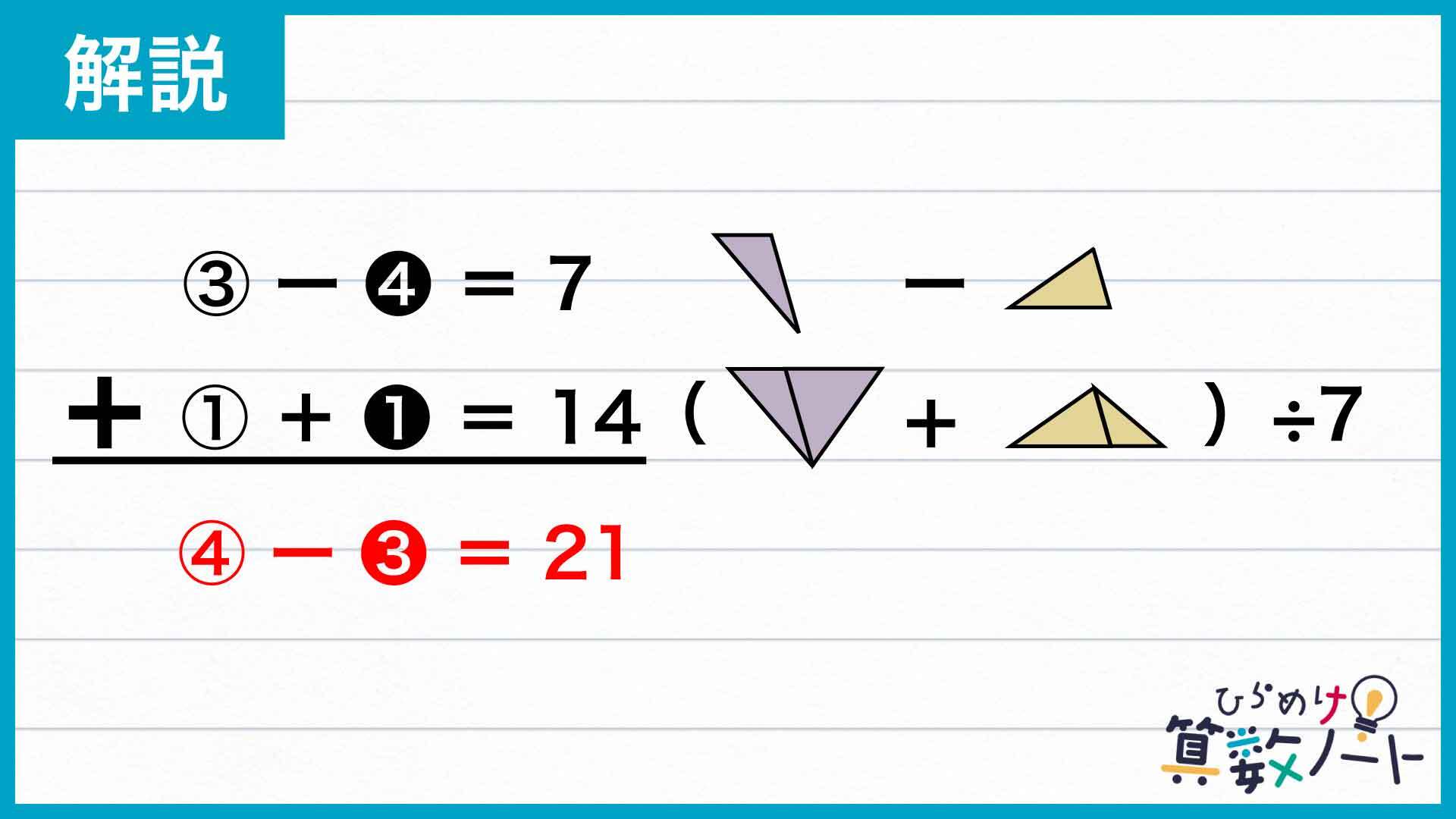
.jpg)









.jpg)







