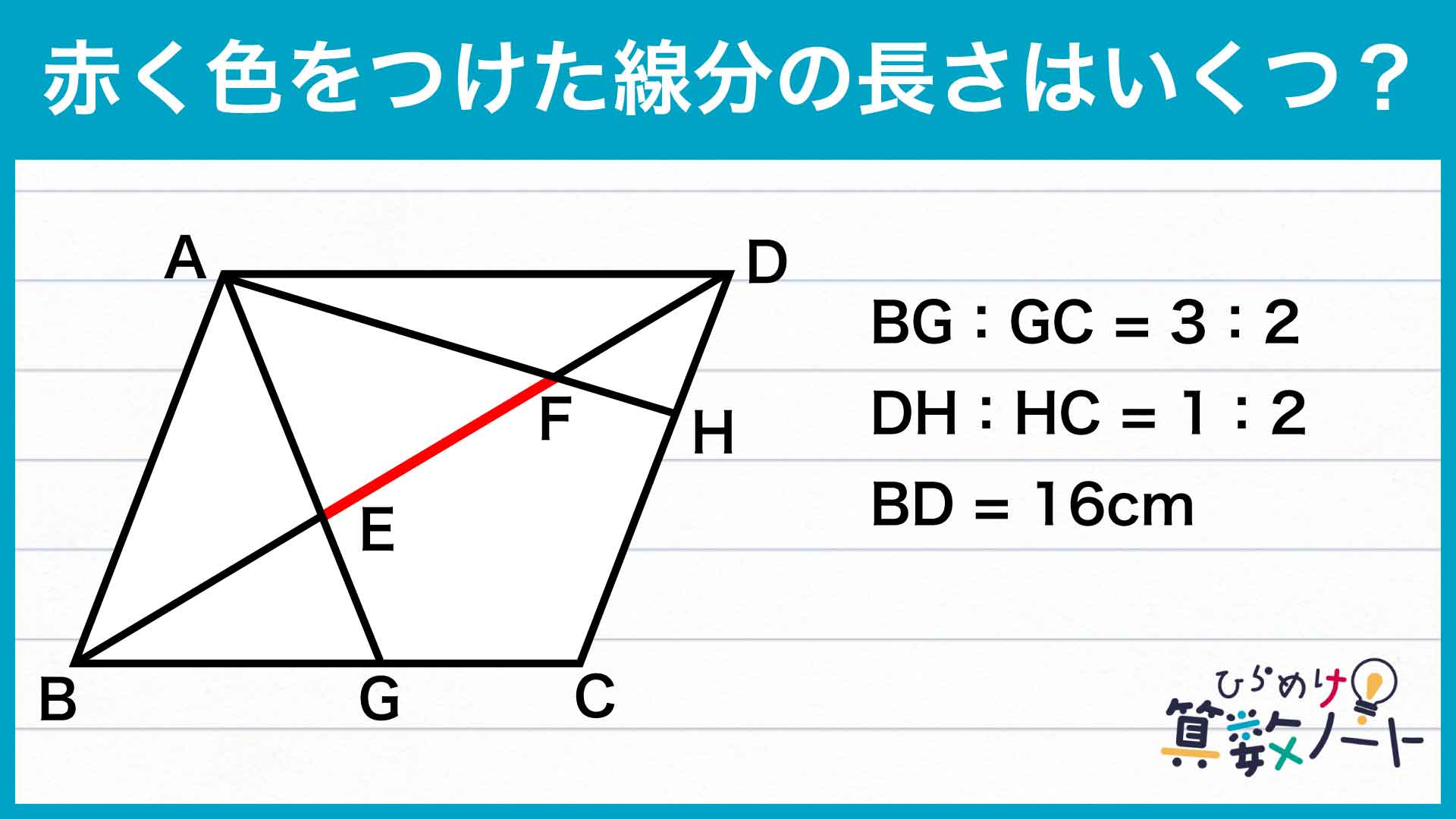
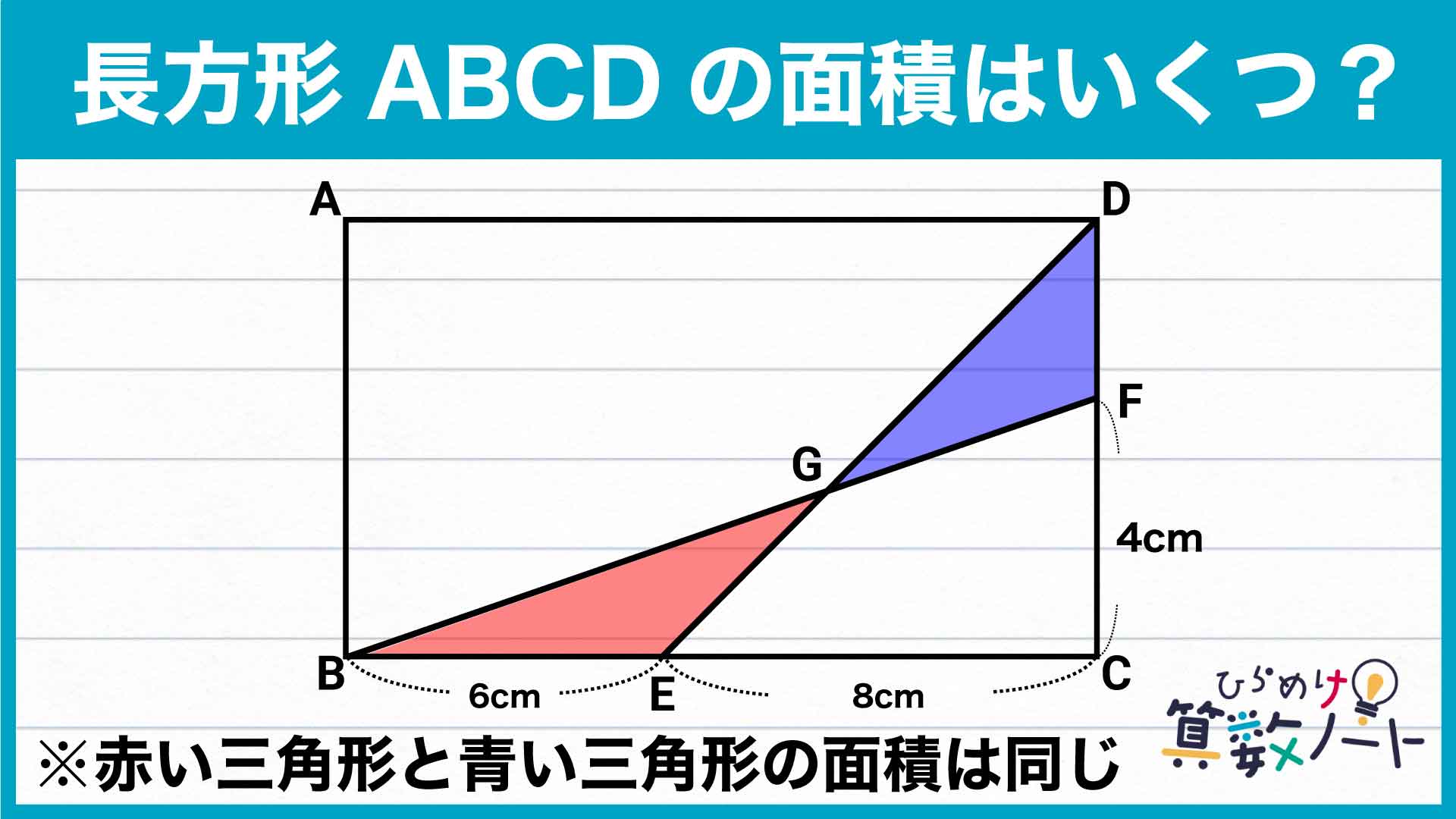
問題はこちら
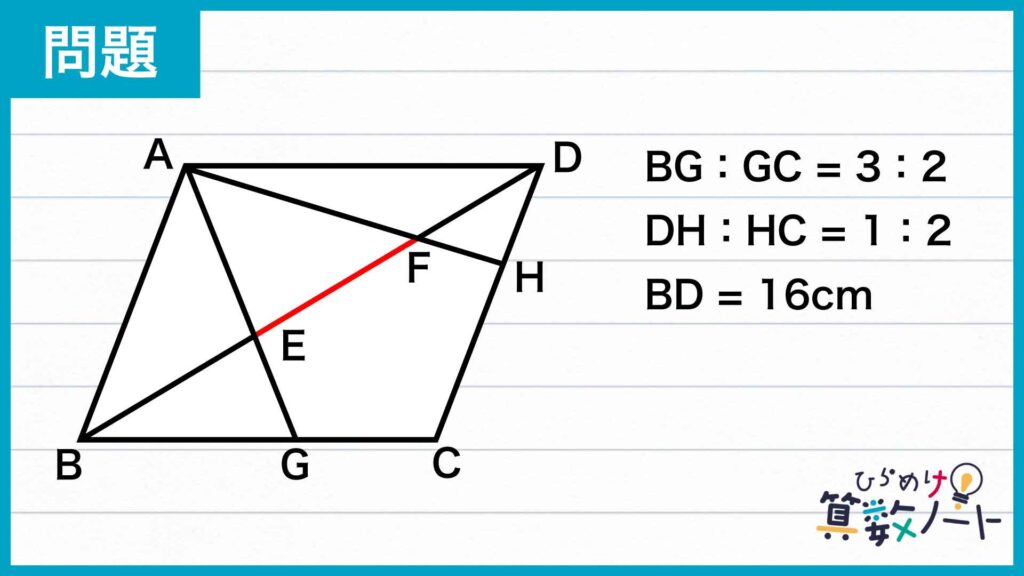
1ページ目:自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
今回の問題を解くうえで重要なポイントを以下にまとめました。
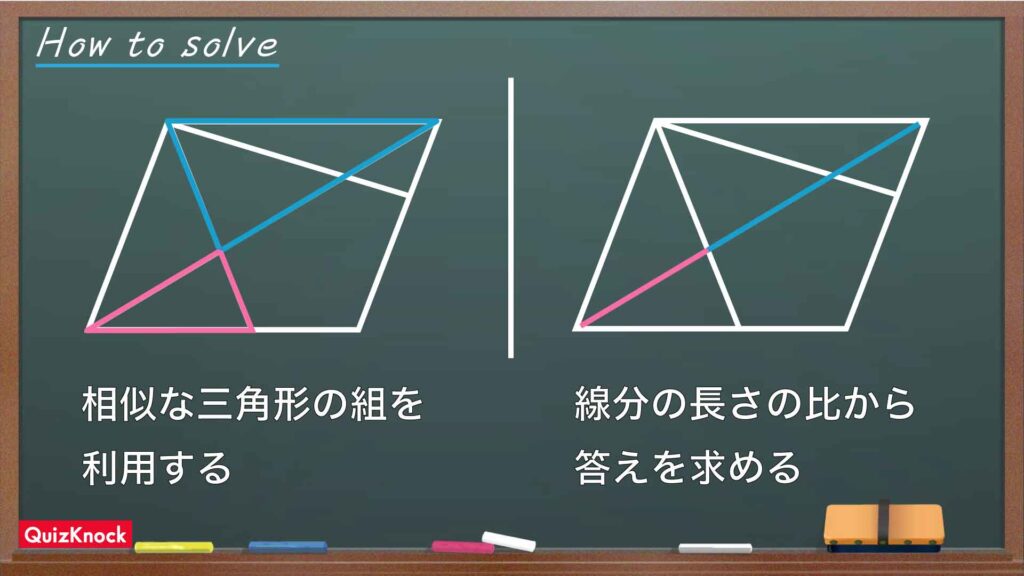
整理すると、
- 相似な三角形の組を利用する
- 線分の長さの比から答えを求める
の2点です。これらのポイントを踏まえながら、問題を解いていきましょう。
相似な三角形の組を利用する
下の図のように、問題の図の中の三角形ADEと三角形GBEに注目します。
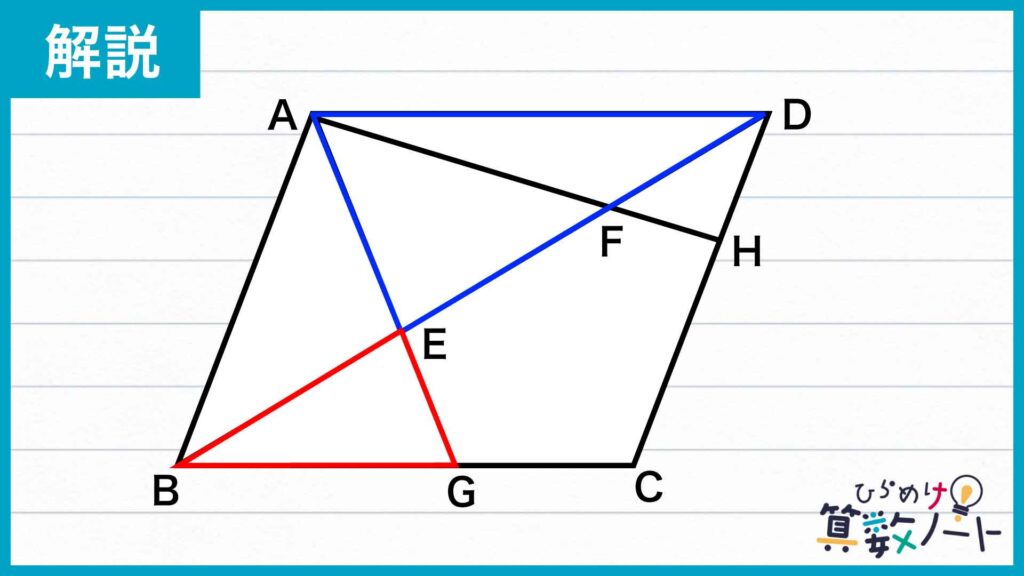
まず、角AEDと角GEBは向かい合う角であるので、その大きさは等しいです。
ここで、下のような平行線についての「錯角の関係」を利用します。
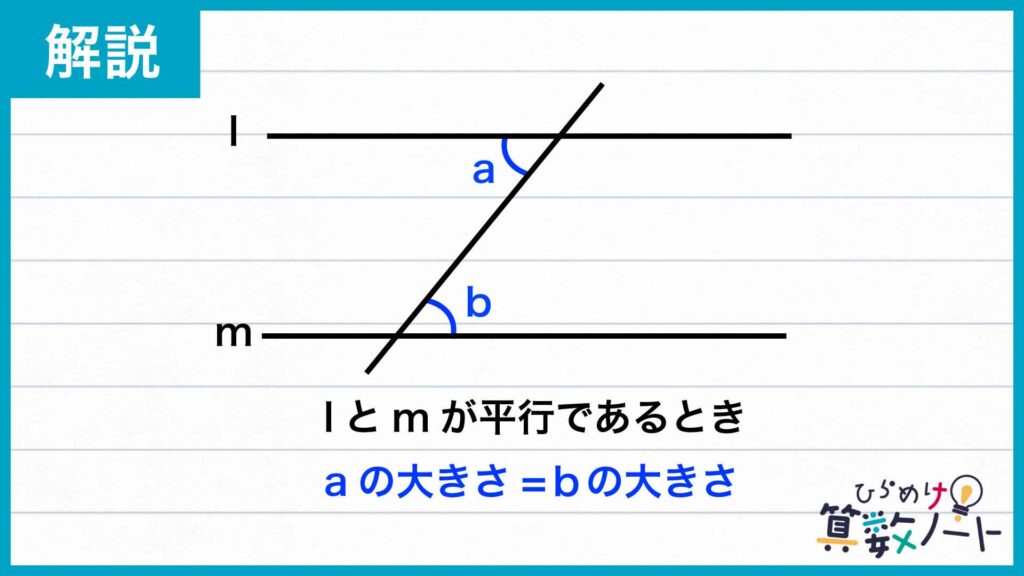
四角形ABCDは平行四辺形であるので、ADとBCは平行です。したがって、平行線についての「錯角の関係」から、角ADEと角GBE、角DAEと角BGEの大きさはそれぞれ等しいことがわかります。よって、「対応する2組の角の大きさがそれぞれ等しい」ことから、三角形ADEと三角形GBEは相似の関係にあることがわかります。
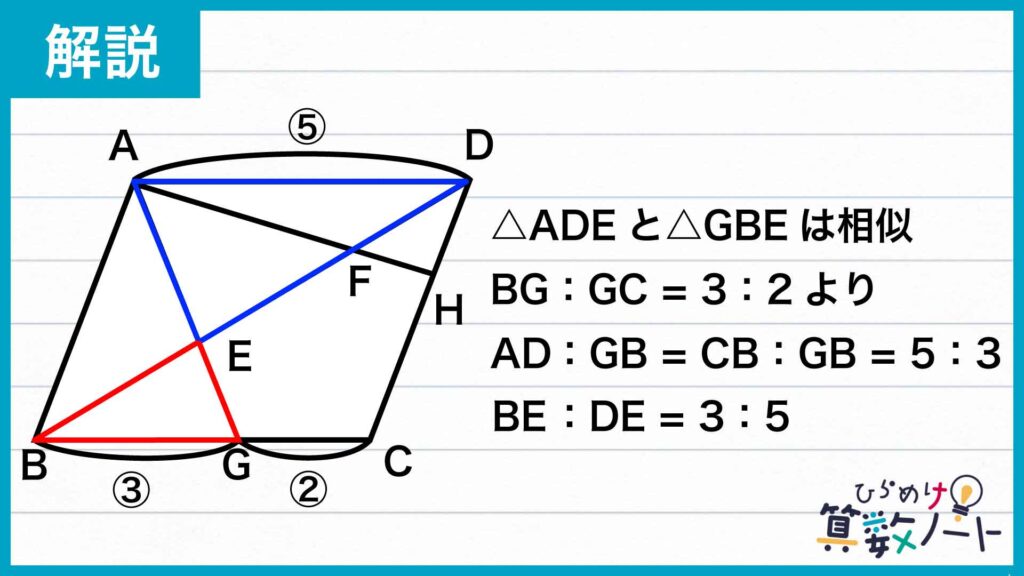
ここで、相似な図形の「対応する辺の比はそれぞれ等しい」という性質を用います。問題の条件から、BG:GC=3:2であり、BG:BC=BG:(BG+GC)=3:5となります。また、平行四辺形の性質からBC=ADであるので、GBとADの長さの比は3:5になります。
三角形ADEと三角形GBEの対応する辺の比は5:3になるので、BEとDEの長さの比は3:5になります。
次に、下の図のようにしてAHとBCを延長していき、その交点をIとします。
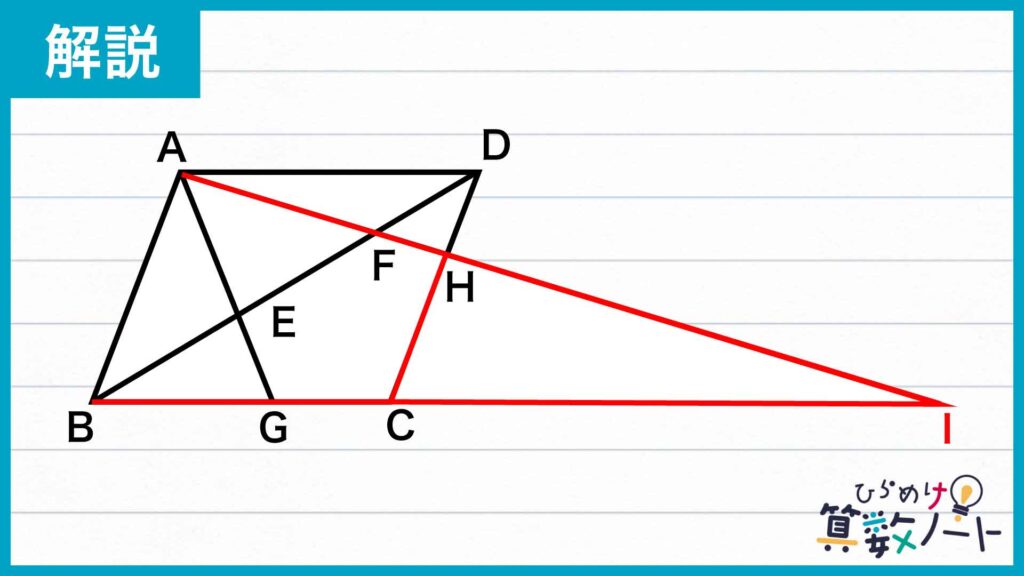
すると、新たに相似な三角形の組を見つけることができます。
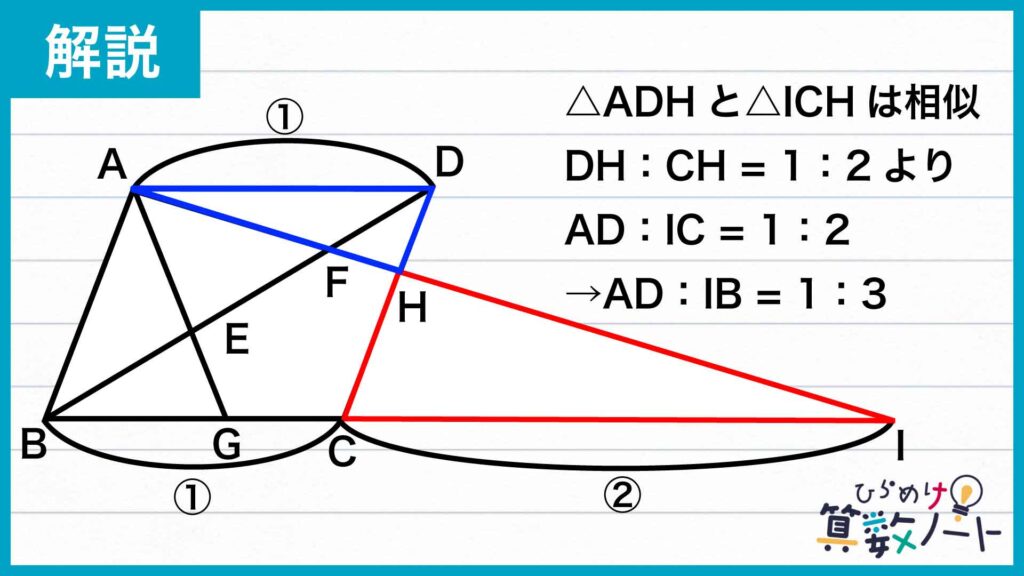
まず、三角形ADHと三角形ICHに注目します。角AHDと角IHCは向かい合う角であるので、その大きさは等しいです。また、「錯角の関係」を利用して、角ADHと角ICH、角DAHと角CIHの大きさも等しいことがわかります。よって、「対応する2組の角の大きさがそれぞれ等しい」ので、三角形ADHと三角形ICHは相似の関係にあります。
ここで、相似な図形の「対応する辺の比はそれぞれ等しい」という性質を用います。問題の条件から、DHとCHの長さの比は1:2なので、ADとICの長さの比も1:2です。平行四辺形の性質よりAD=BCであることを用いると、AD:IB=AD:(IC+CB)=AD:(IC+AD)=AD:(3×AD)=1:3であることがわかります。
次に、三角形AFDと三角形IFBに注目します。角AFDと角IFBは向かい合う角であるので、その大きさは等しいです。また、先ほどの「錯角の関係」を利用すると、ADとBIが平行であることから、角ADFと角IBF、角FADと角FIBの大きさも等しいです。よって、「対応する2組の角の大きさがそれぞれ等しい」ことから、三角形AFDと三角形IFBは相似の関係にあります。
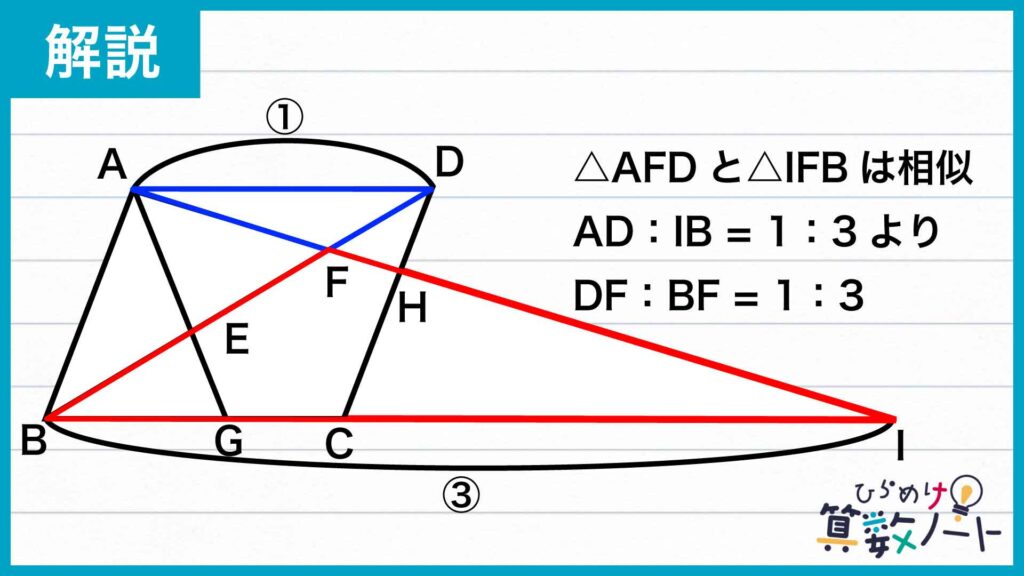
ここで再び、相似な図形の「対応する辺の比はそれぞれ等しい」という性質を用います。AD:IB=1:3であることから、DFとBFの長さの比も1:3であることがわかります。
線分の長さの比から答えを求める
ここまでで、DEとBEの長さの比は5:3であることと、DFとBFの長さの比が1:3であることがわかりました。ここで、BDのみを取り出して考えてみましょう。
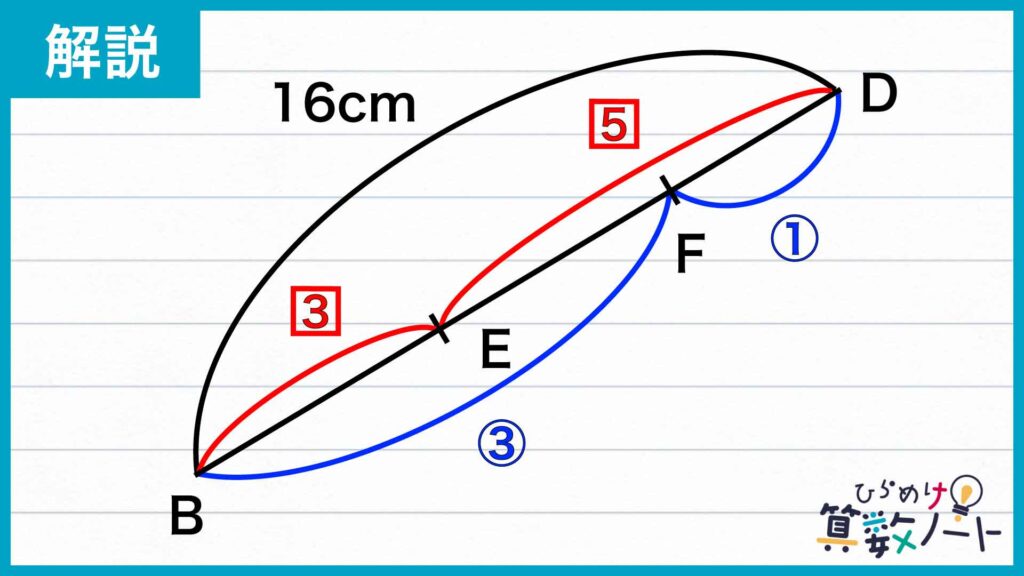
DEとBEの長さの比は5:3なので、BE:BD=BE:(DE+BE)=3:8であることがわかります。BDの長さは16cmなので、BE:16=3:8、これを解くとBEの長さは6cmとなります。
さらに、DFとBFの長さの比は1:3であり、DF:BD=BF:(DF+BE)=1:4であることがわかります。BDの長さは16cmなので、DF:16=1:4、DFの長さは4cmとなります。
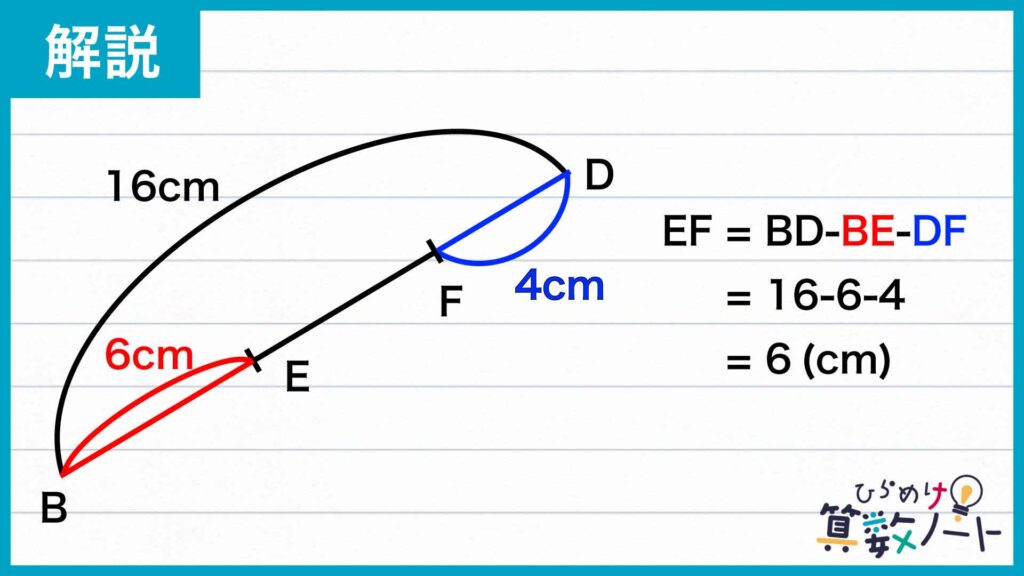
したがって、求めるEFの長さは、EF=BD-(BE+DF)=6(cm)です。
答え:6cm
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)








.jpg)







