ヒント
下の図のように、問題の図の中の三角形ADEと三角形GBEに注目します。
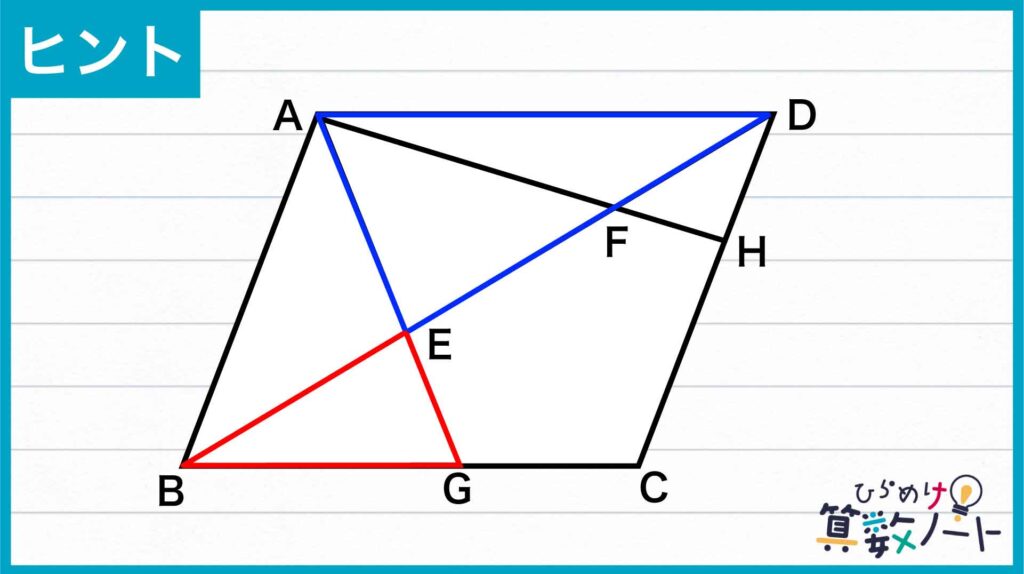
まず、角AEDと角GEBは向かい合う角であるので、その大きさは等しいです。
ここで、下のような平行線についての「錯角の関係」を利用します。
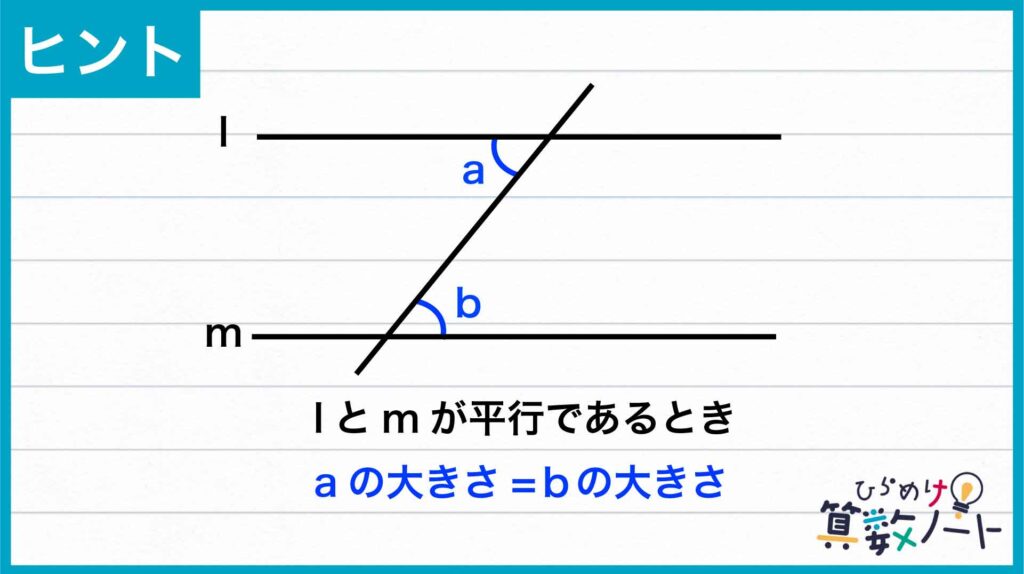
四角形ABCDは平行四辺形であるので、ADとBCは平行です。したがって、平行線についての「錯角の関係」から、角ADEと角GBE、角DAEと角BGEの大きさはそれぞれ等しいことがわかります。よって、「対応する2組の角の大きさがそれぞれ等しい」ことから、三角形ADEと三角形GBEは相似の関係にあることがわかります。
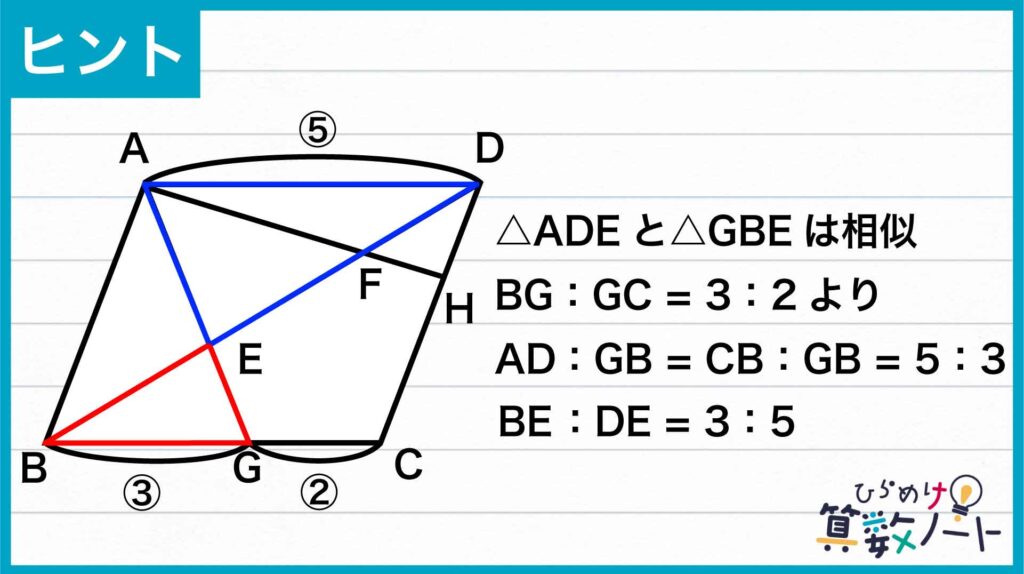
ここで、相似な図形の「対応する辺の比はそれぞれ等しい」という性質を用います。問題の条件から、BG:GC=3:2であり、BG:BC=BG:(BG+GC)=3:5となります。また、平行四辺形の性質からBC=ADであるので、GBとADの長さの比は3:5になります。
三角形ADEと三角形GBEの対応する辺の比は5:3になるので、BEとDEの長さの比は3:5になります。