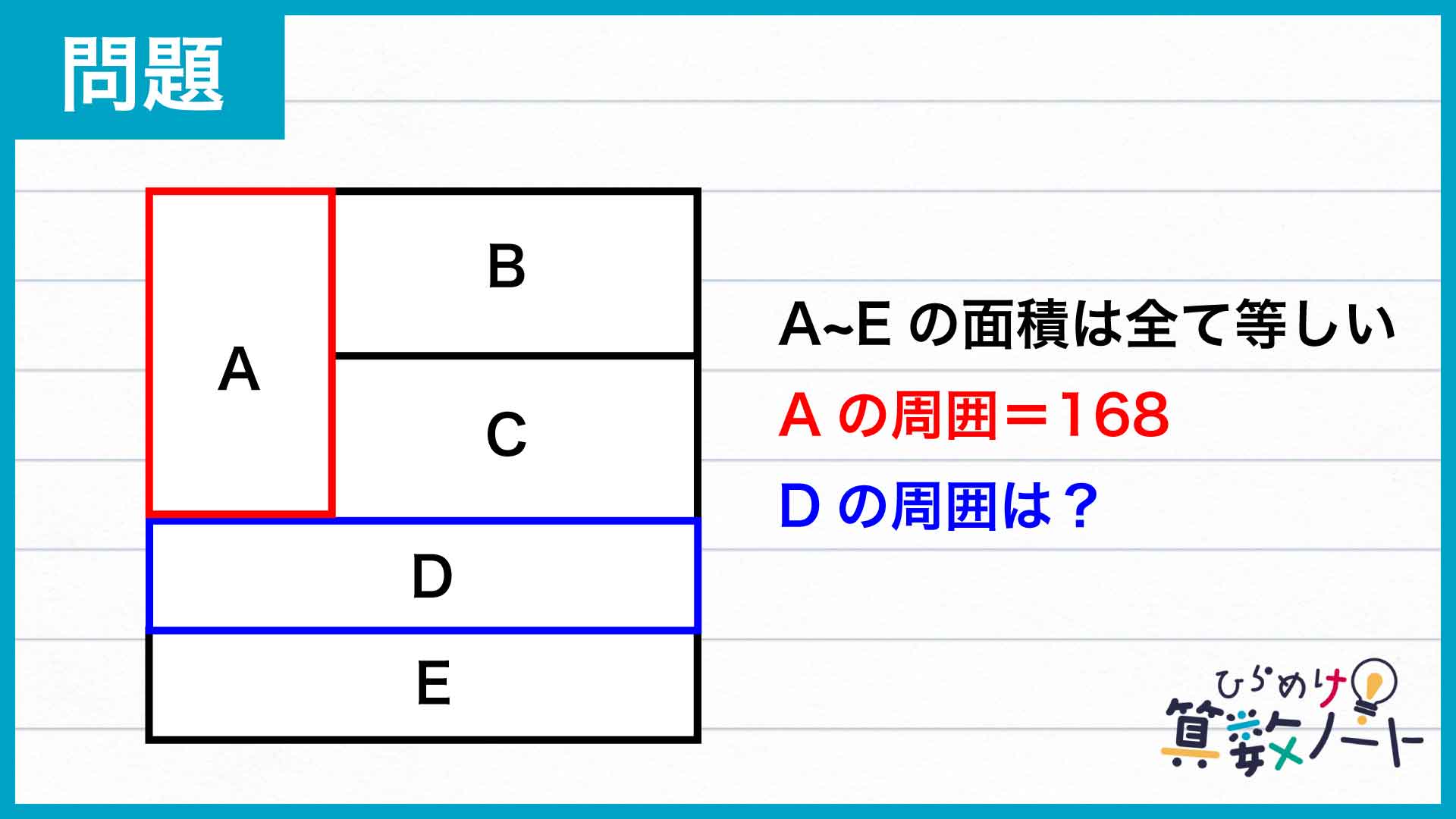
問題はこちら
1ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の解説です
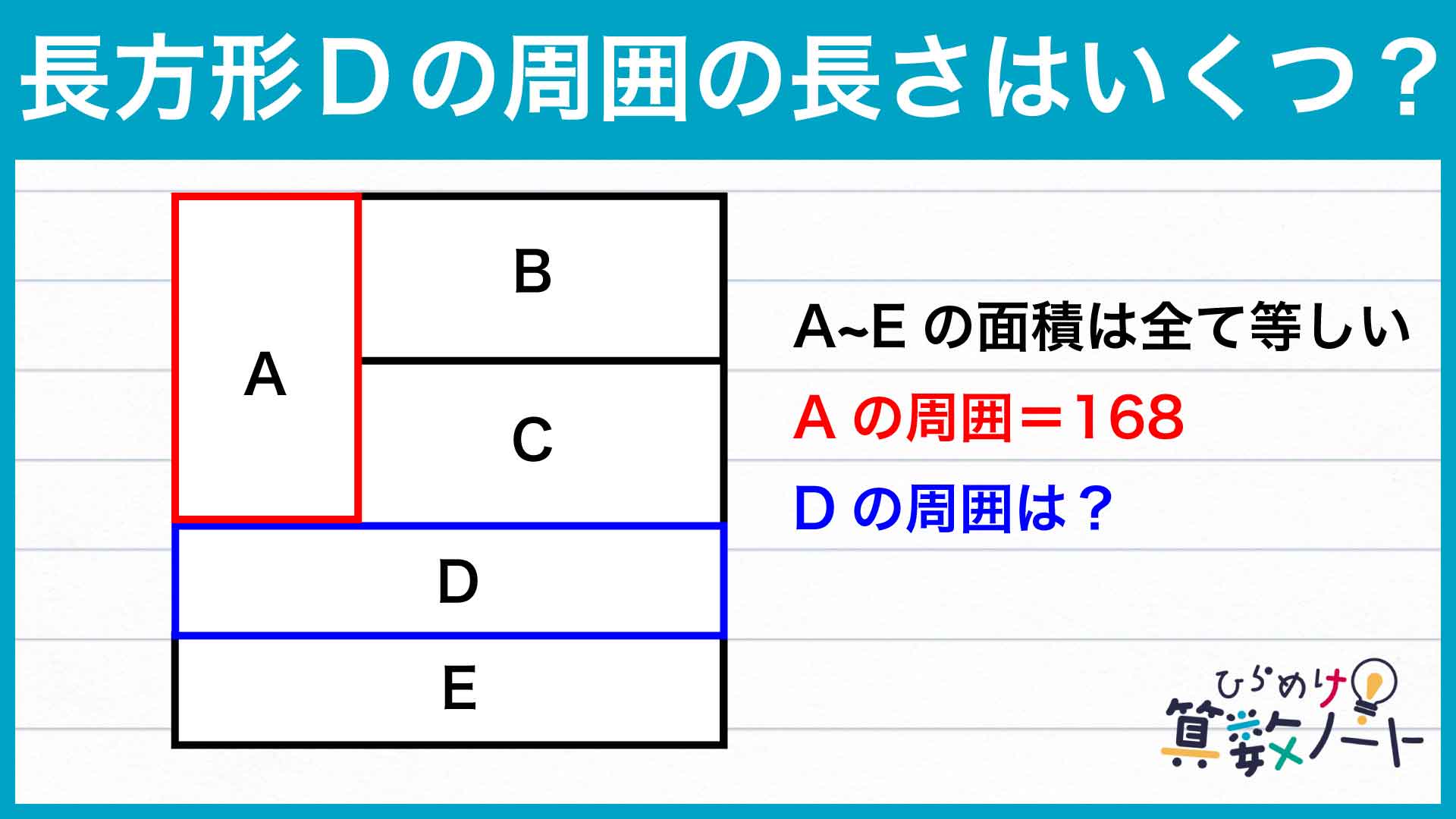
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
この問題の解き方をまとめた図がこちらです。
ポイントは、分割された縦の辺、横の辺についてそれぞれ考えたあと、比を統一することです。
では、このポイントを踏まえつつ解いていきましょう!
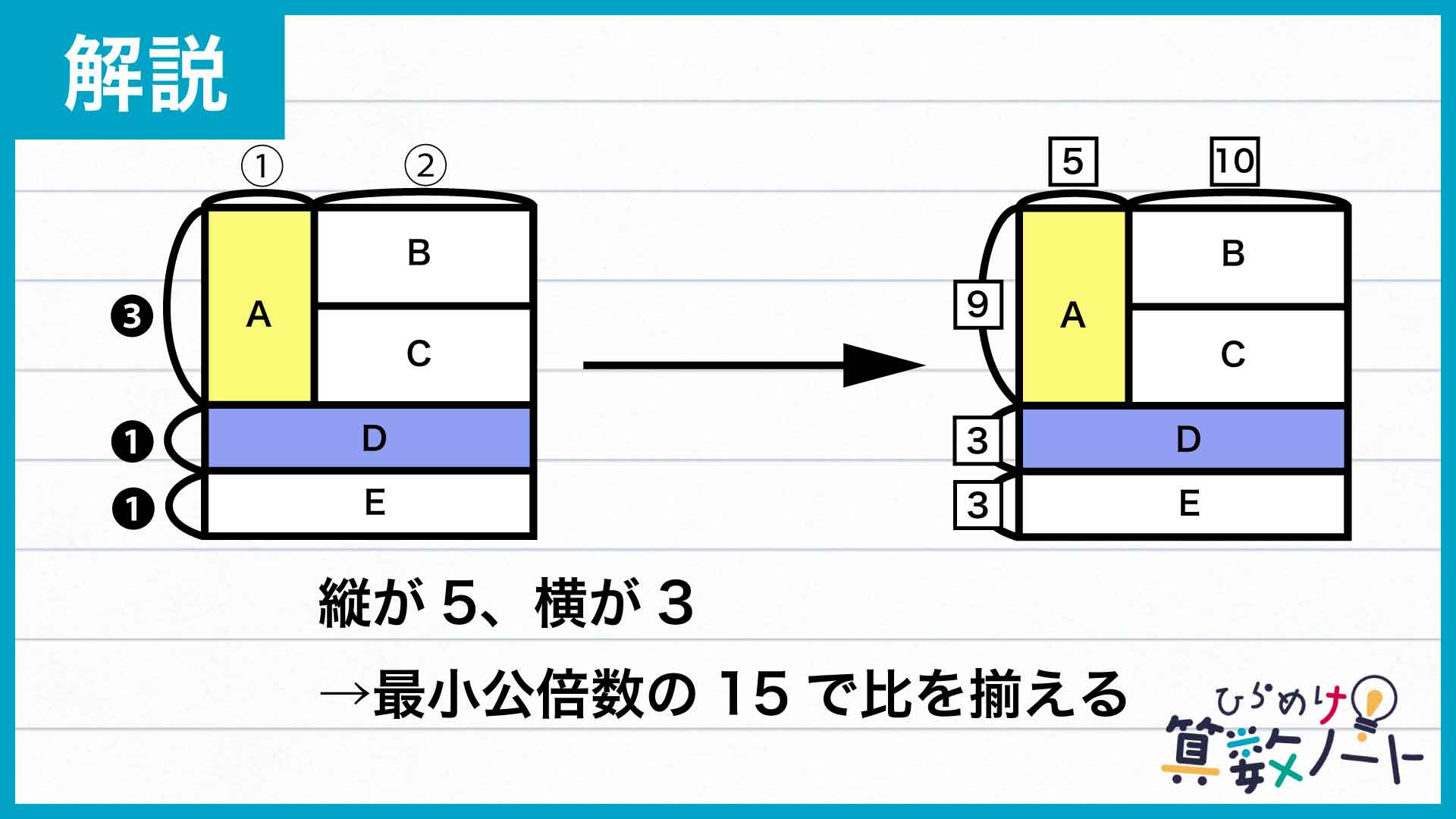
縦・横の辺の分割について考える
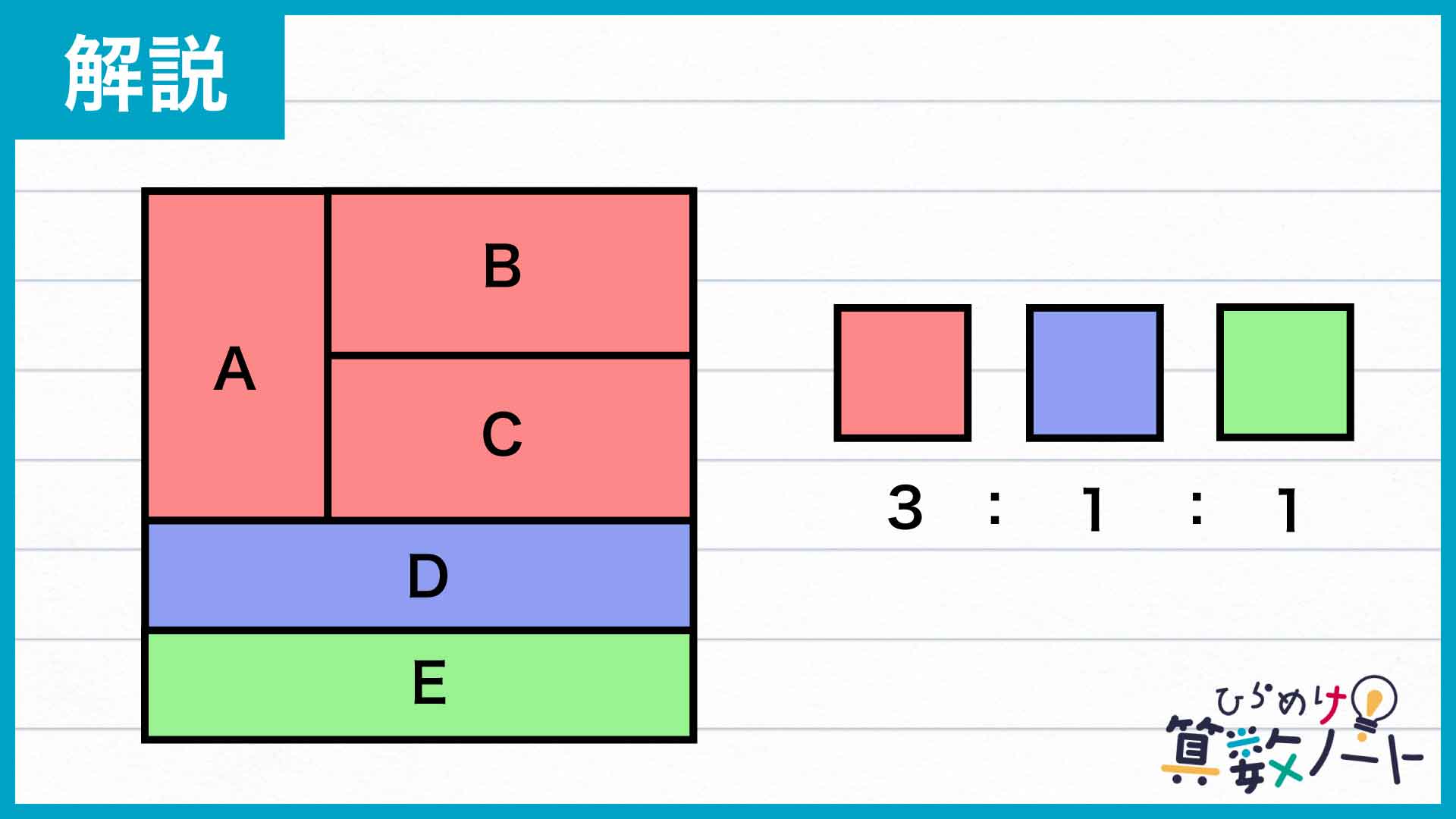
注目すべきは、長方形A〜Eの面積が全て等しいということです。このことから、複数の長方形を組み合わせた大きな図形と元の長方形の面積比を、簡単な整数比で表すことができます。
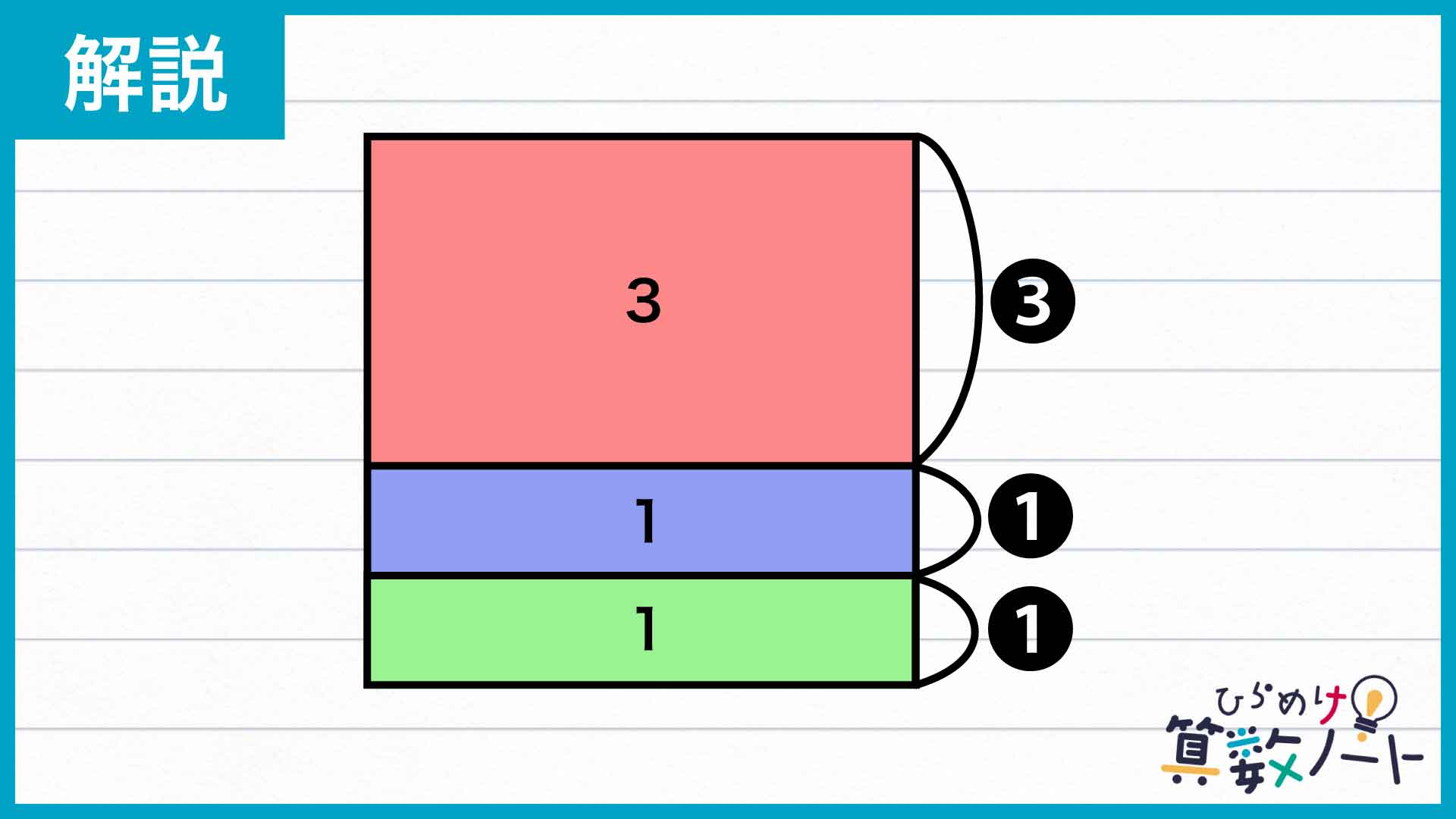
たとえば、A・B・Cの3つを合体させてできる大きな長方形について考えてみましょう。この図形の面積は、下にあるDやEの面積のちょうど3倍です。
A+B+C、D、Eの3つの長方形はいずれも横の辺の長さが等しくなっています。したがって、面積の比はそのまま縦の辺の長さの比に等しいのです。このことから、正方形の縦の辺は図のように上から3:1:1に分割されていることがわかります。
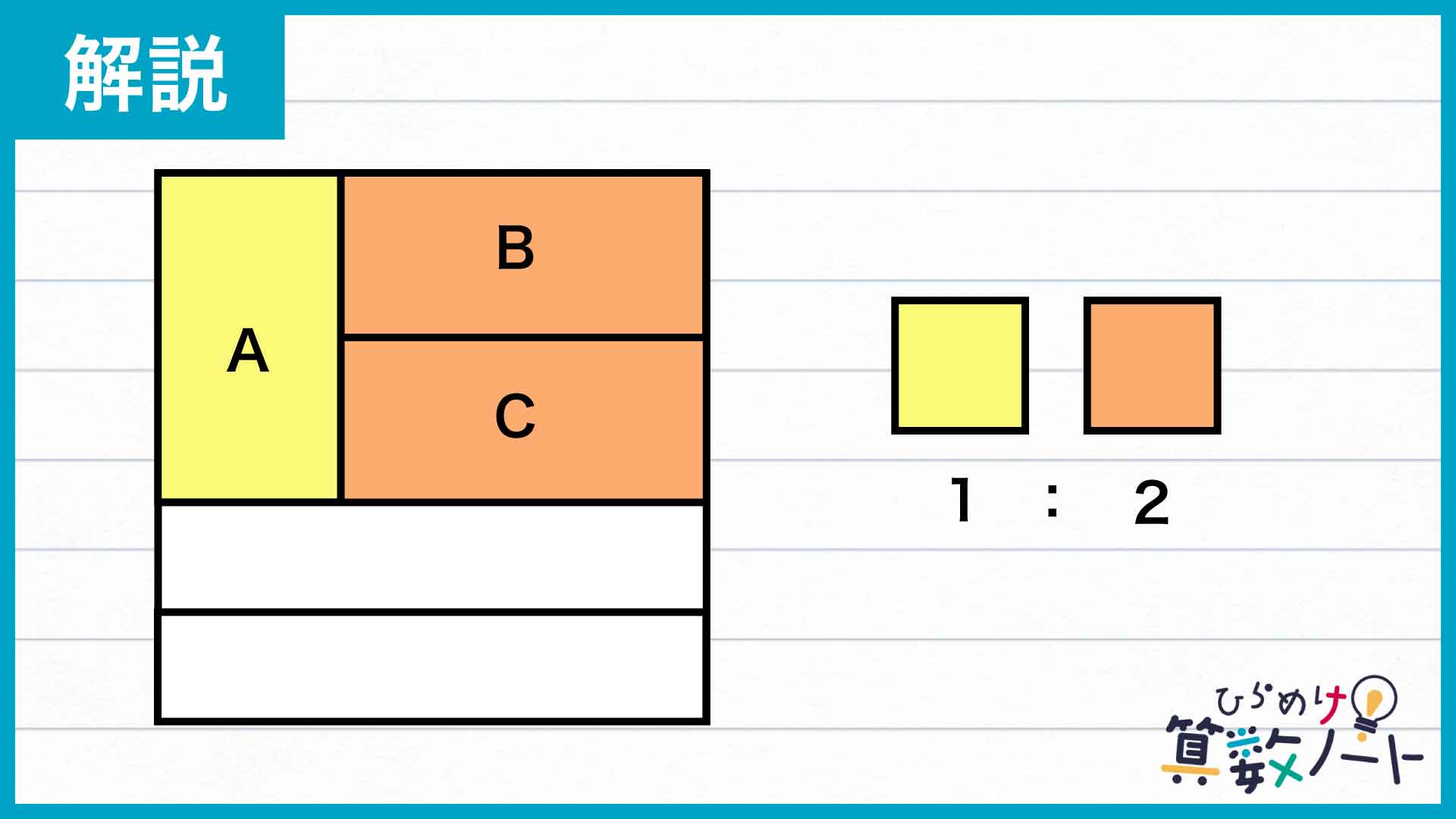
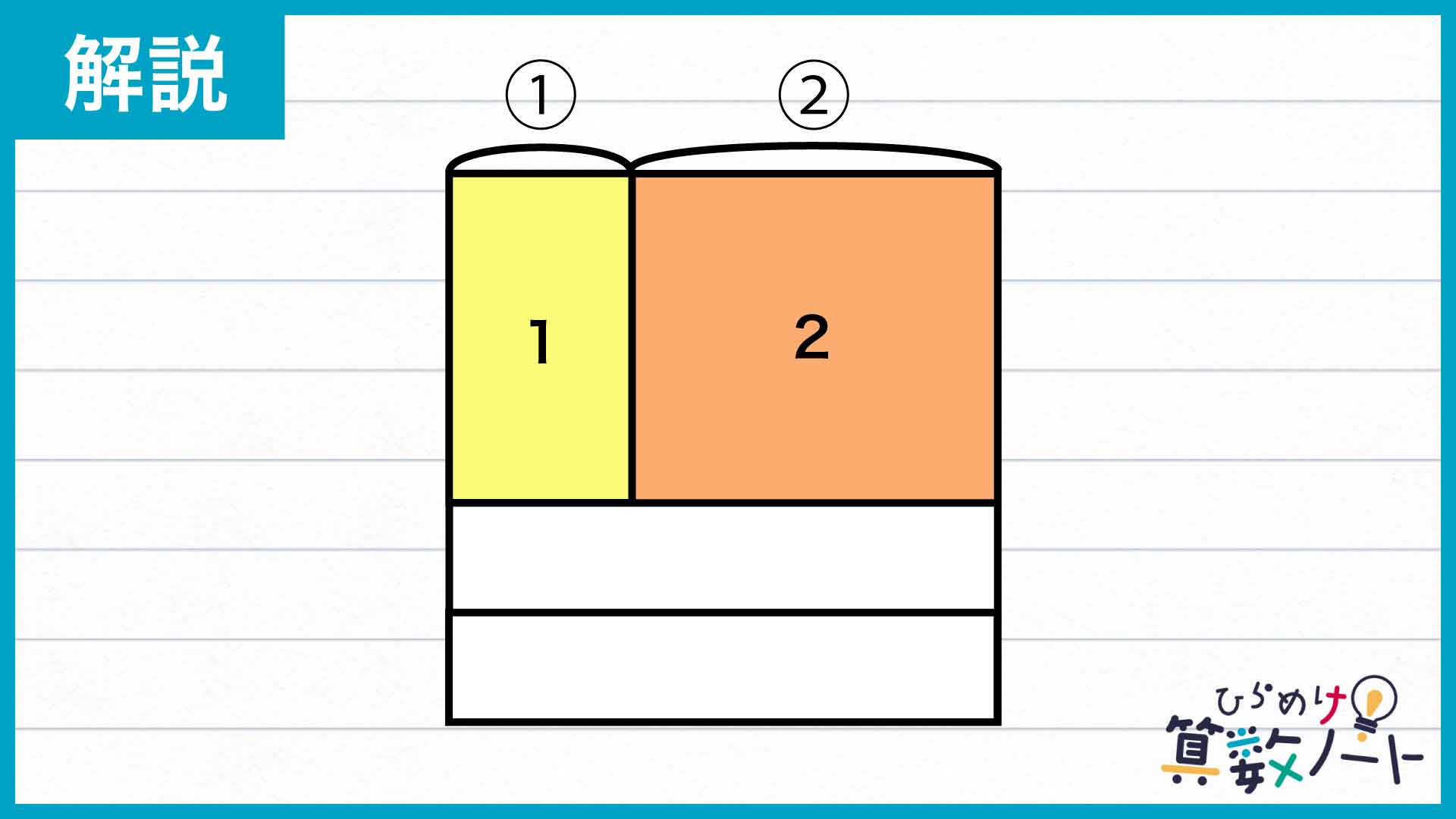
同様に、B・Cの2つを合体させた長方形についても考えてみます。この図形の面積は、左にあるAの面積のちょうど2倍です。
B+CとAと縦の辺の長さが等しいため、面積の比はそのまま横の辺の長さの比になります。このことから、正方形の横の辺は左から1:2に分割されていることがわかります。
比を統一して考える
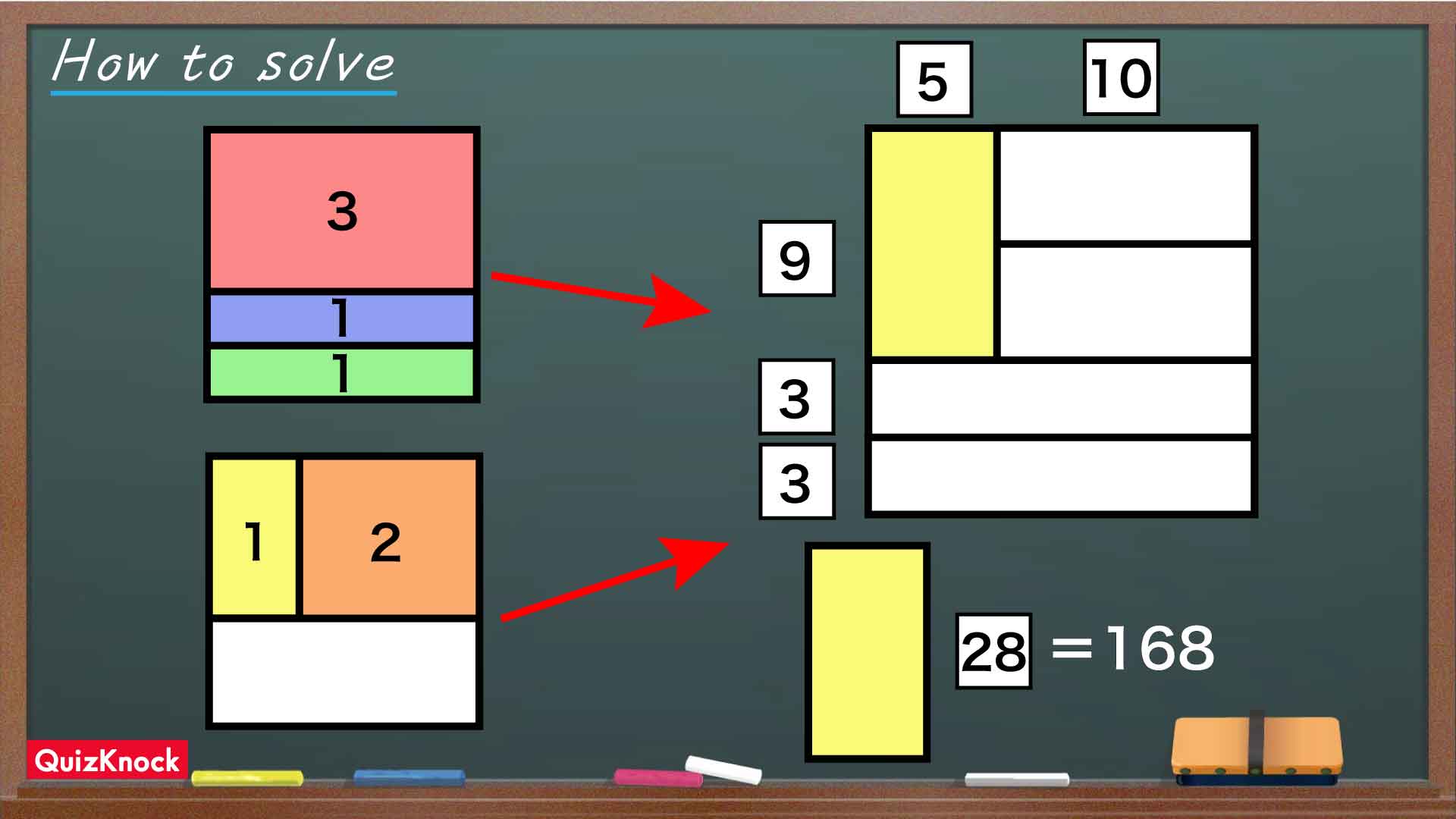
ここまでで、正方形の辺が縦に3:1:1、横に1:2の比で分割されていることがわかりました。正方形の縦・横の辺の長さは同じなので、分割された長さの合計が等しくなるように比を直してみましょう。今回は縦が3+1+1で5、横が1+2で3なので、それらの最小公倍数である15に揃えてみます。
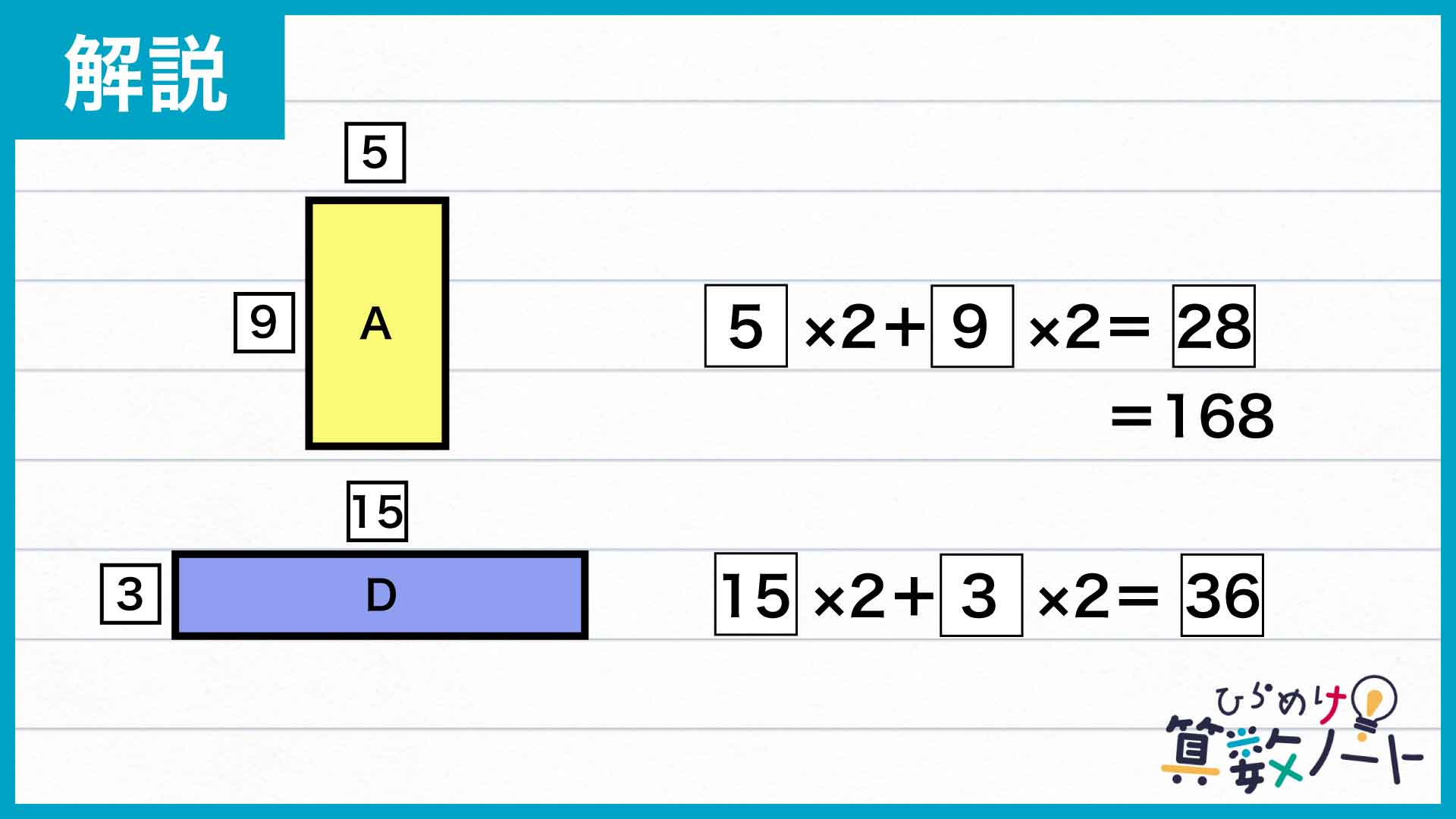
この比において、Aの周囲の長さは5×2+9×2=28に相当します。また、Dの周囲の長さは同様に15×2+3×2=36と表されます。
Aの周囲の長さは168なので、実際の辺の長さは比で表された値の168÷28=6倍にあたります。したがって、求めるDの周囲の長さは36×6=216であるとわかるのです。
答え:216
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)








.jpg)







