小学6年生で解ける「図形の面積」を求める問題に挑戦！あなたはひらめけますか？

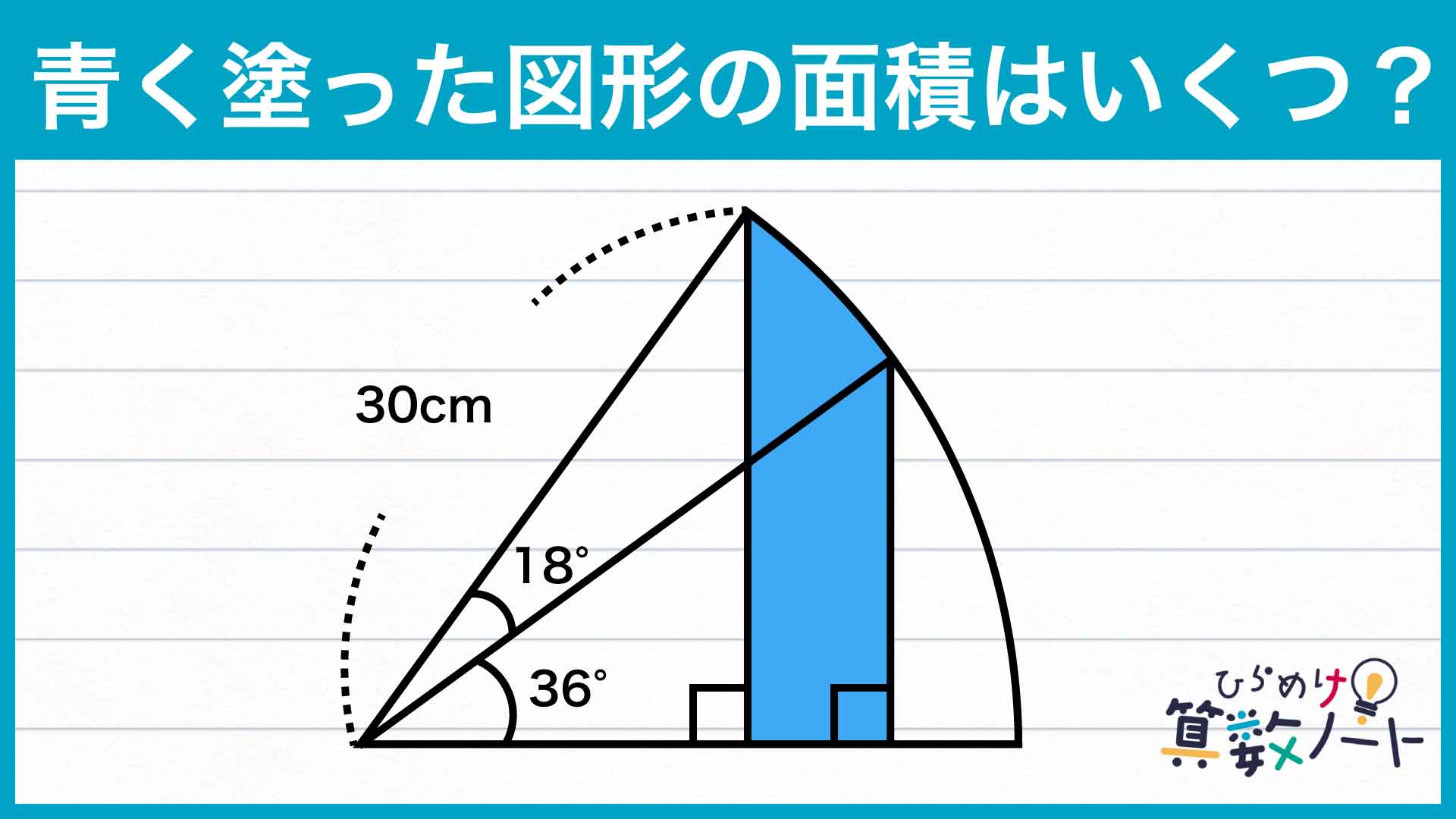
問題はこちら

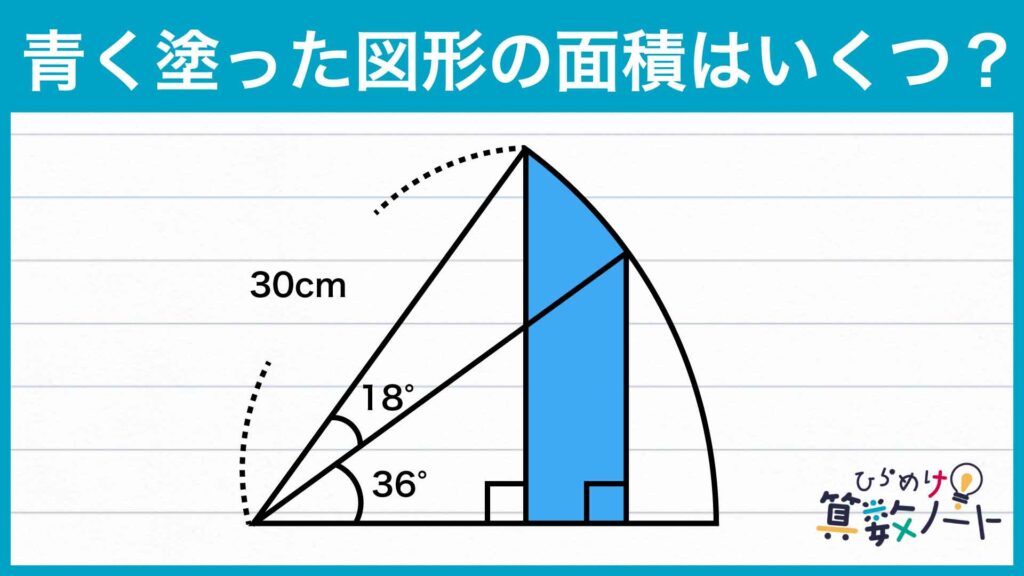
前ページ：【解答フォーム】自力で解きたい方はこちらへ！　以下は問題の答えです

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

今回の解き方をまとめた図がこちらです。

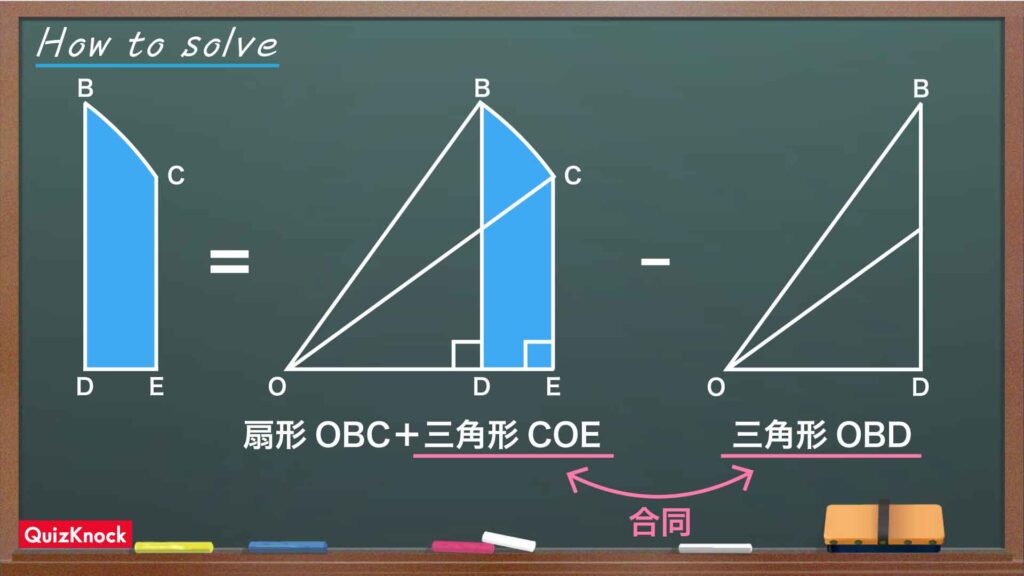
今回のポイントは「図形の中にある図形同士の関係性を活用する」ことです。

このポイントをもとに、問題を攻略していきましょう！

図形の中の図形を観察する

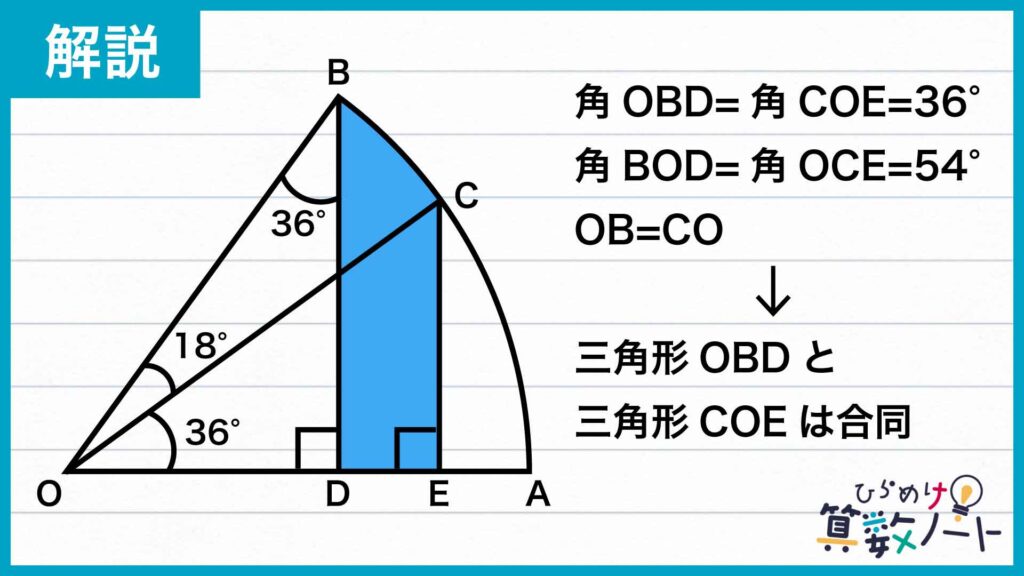
まず、下の図のように点O、A、B、C、D、Eを置きます。

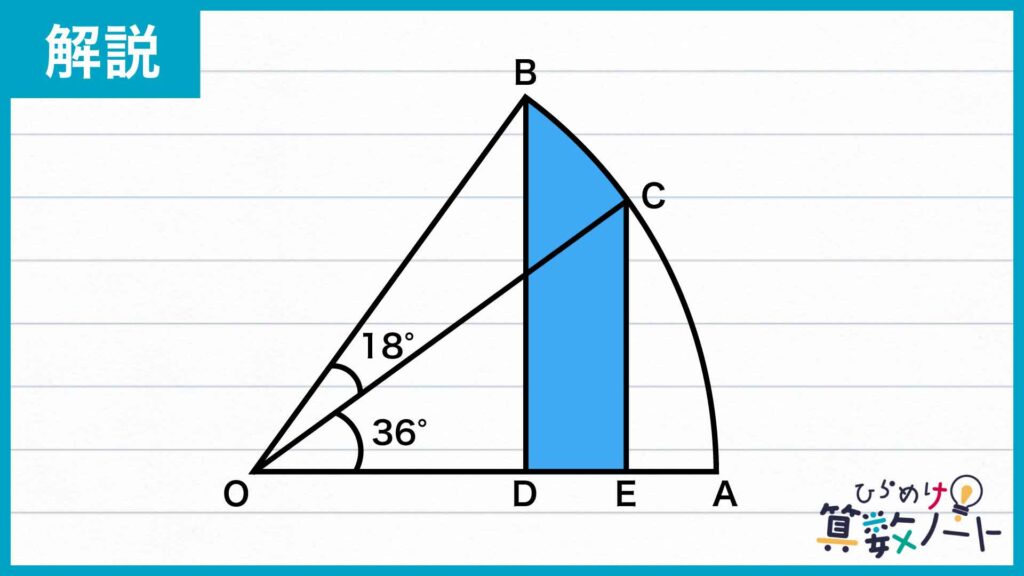
ここで、三角形OBDと三角形COEに注目します。

まず、角OBD=180-(90+36+18)=36度なので、角OBD=角COEです。

問題の条件より角CEO=90度なので、角OCE=180-(36+90)=54度です。また、角BOD=18+36=54度なので、角BOD=角OCEであることがわかります。

さらに、扇形の半径なのでOB=COです。

一辺とその両端の角の大きさがそれぞれ等しいことから、三角形OBDと三角形COEは合同であることがわかります。

合同な三角形を活用する

ここからは、青色に塗られた図形の面積を求める方法を考えます。

図形を観察すると、青色に塗られた図形の面積は、扇形OBCと三角形COEが合体した図形の面積から、三角形OBDの面積を引くことで求められることがわかります。

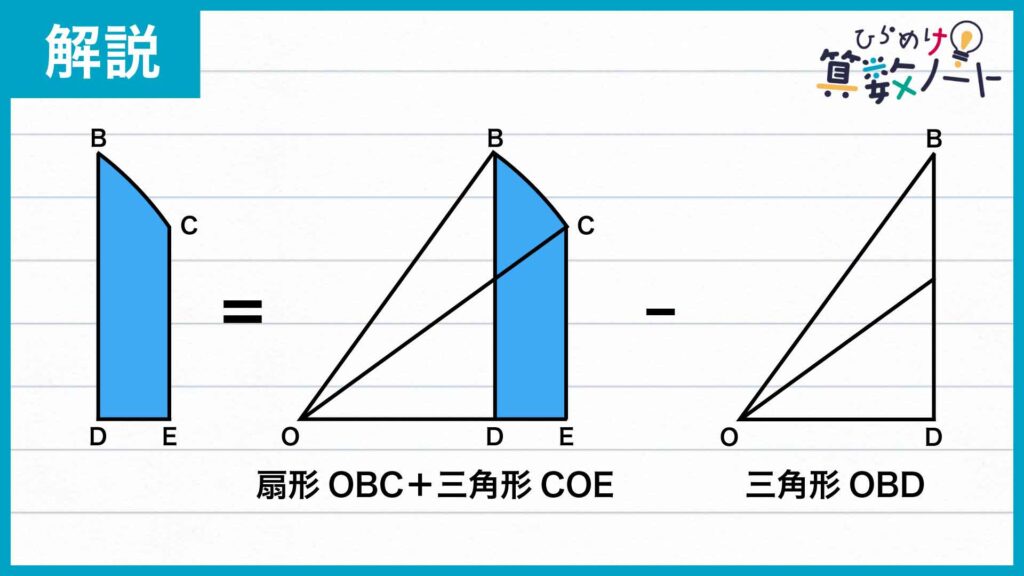
ここで、先ほど見つけた「三角形OBDと三角形COEは合同な図形である」という関係性を活用します。合同ということは面積が等しいということです。

したがって、上記の式において三角形COEと三角形OBDの面積が相殺され、青色に塗られた図形の面積は扇形OBCの面積と等しいことがわかります。

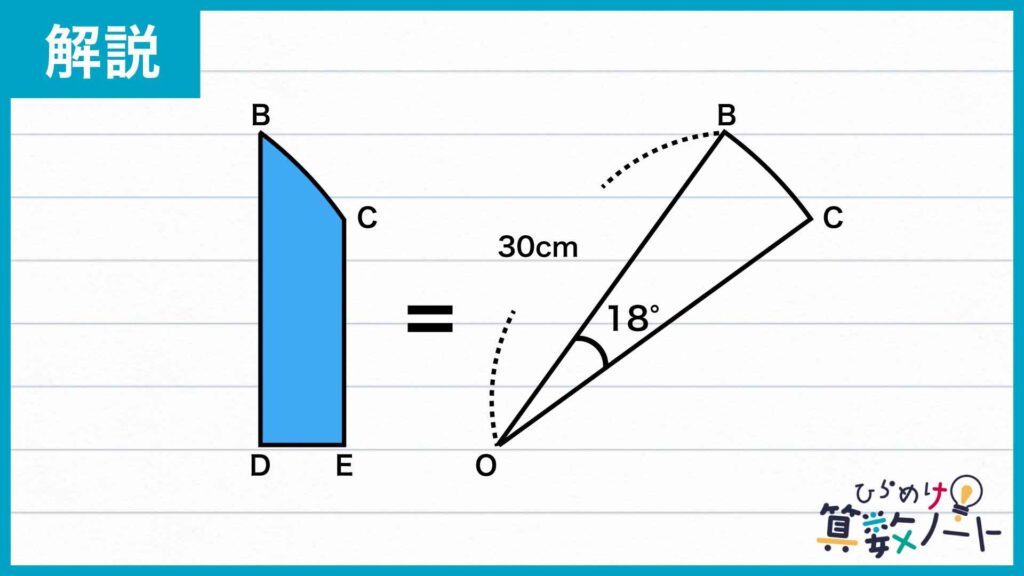
中心角の大きさは18度です。円は1周360度なので、この扇形は円の面積の18/360=1/20の面積です。

以上より、青色に塗られた図形の面積は、30×30×π×1/20=45πcm²となります。

答え：45πcm²

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】