まだ問題を見ていない方はこちら
1ページ目:【15秒以内に解ける?】自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
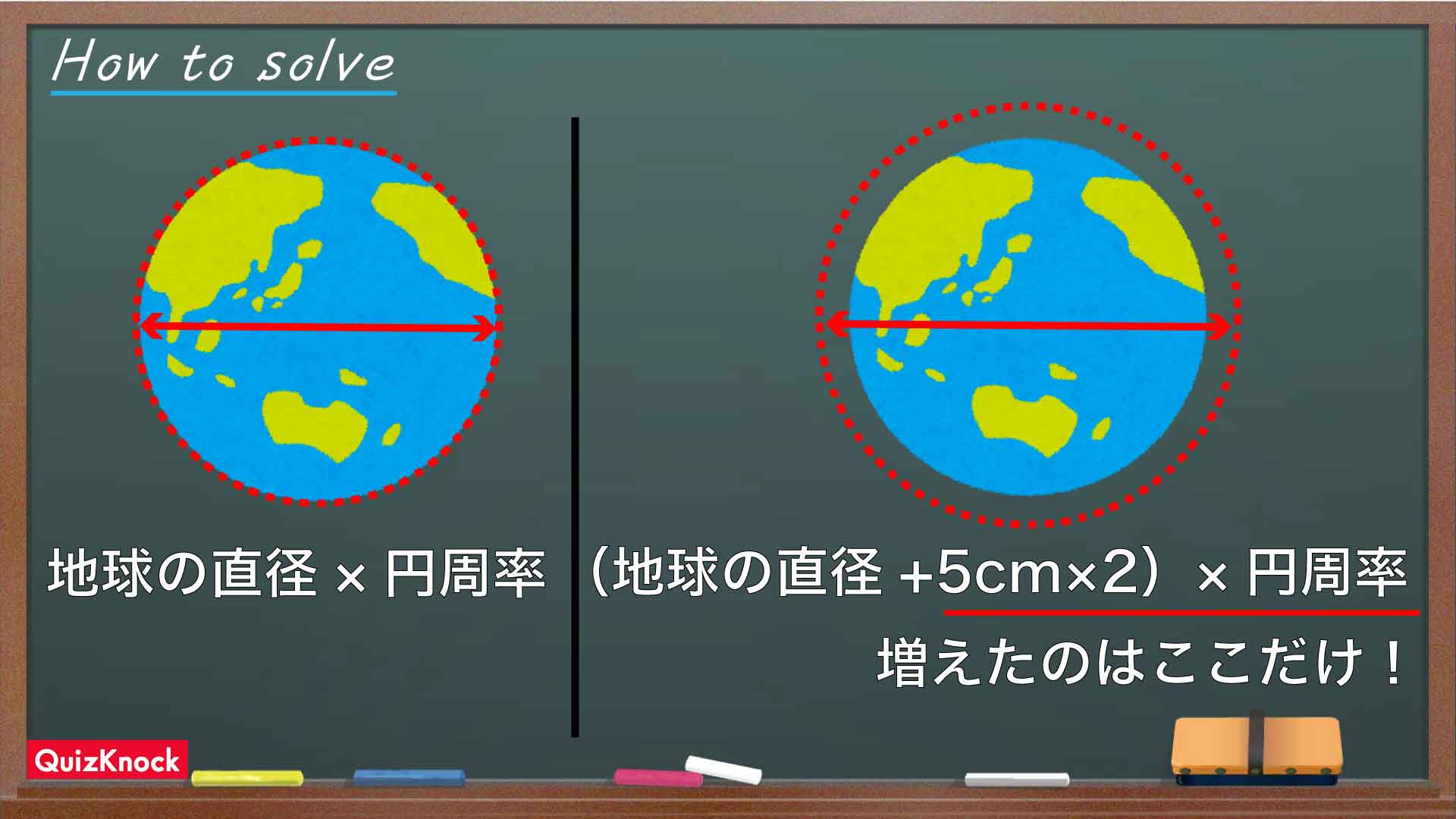
この問題の解き方をまとめた図がこちらです。
ポイントは、地球の大きさに惑わされず円周の求め方を考えることです。
では、このポイントを踏まえつつ解いていきましょう!
円周の求め方は?
小学校で習った「円周の求め方」をもう一度おさらいしてみましょう。円周は直径×円周率という式で計算することができますね。地球を大きな球体とみなせば断面は円なので、1周の距離は同じ式で求められます。
次に、巻き尺を地面から5cm浮かせて巻きつけた場合を考えてみましょう。1周するときの半径は巻き尺を浮かせた分だけ長くなるので、測る長さは下の図に示した式から求めることができます。
ここでポイントになるのが、小学校で習った「分配法則」です。桁数の多い数でかけ算をするときなどに使われる重要な法則ですが、みなさんは覚えていますか?
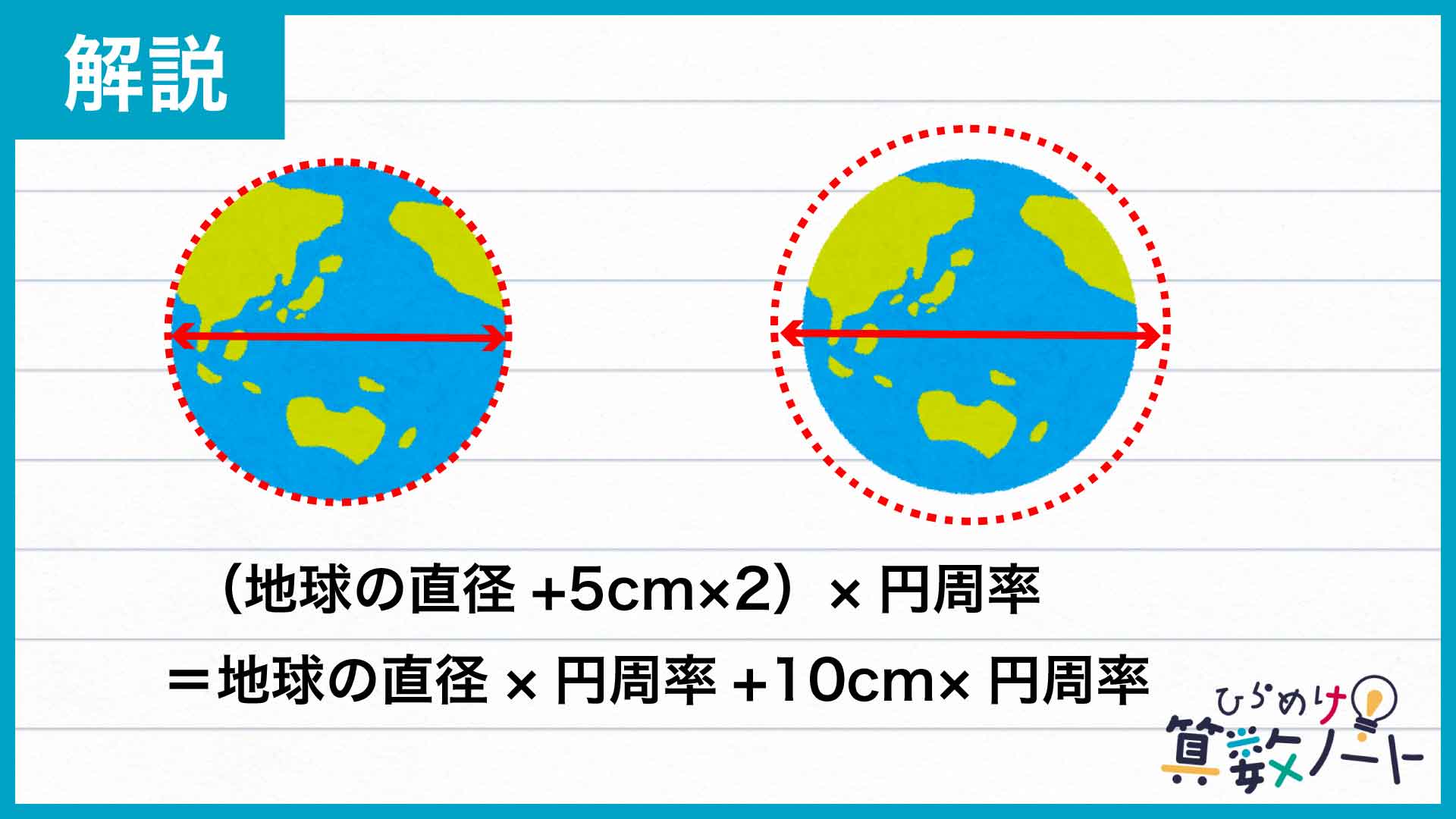
この法則に従えば、巻き尺を浮かせたときの長さを求める式は次のように変形することができます。
つまり、巻き尺を浮かせる前と比べて増えたのは10cm×円周率の部分だけということがわかるのです。円周率をだいたい3.14として、増えた長さは10cm×3.14=31.4cm。国際大会などで使われるソフトボールの大きさは外周が約30.2cm〜30.8cmとされているので、同じくらいの長さということになります。
答え:ソフトボールの外周
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】














.jpg)









.jpg)







