小学5年生で解ける「三角形の面積」を求める問題にチャレンジ！

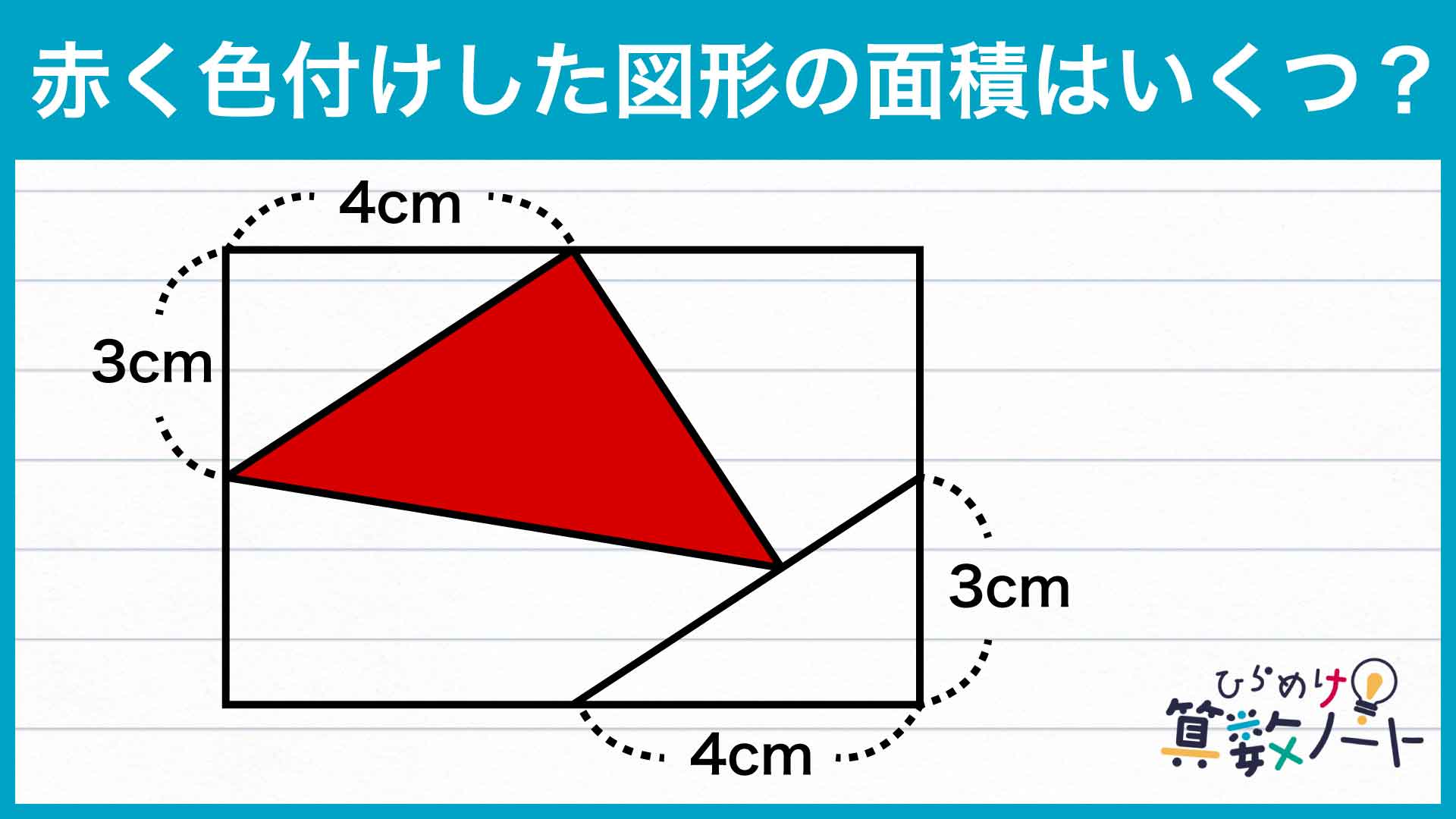
問題はこちら

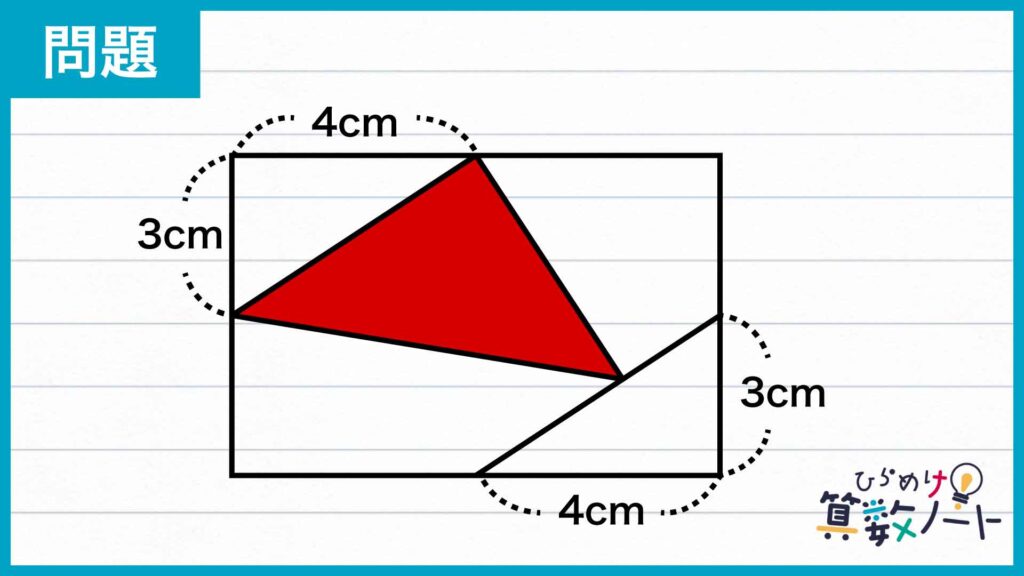
前ページ：【解答フォーム】自力で解きたい方はこちらへ！　以下は問題の答えです

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

今回のポイントは、「等積変形を利用する」ことです。このポイントをもとに、問題を攻略していきましょう！

等積変形を使う

赤色の三角形は底辺の長さと高さがわからないため、このままでは面積を求めることができません。ここから、面積を求められる形に変形していきます。

ここで、次のような性質を利用します。

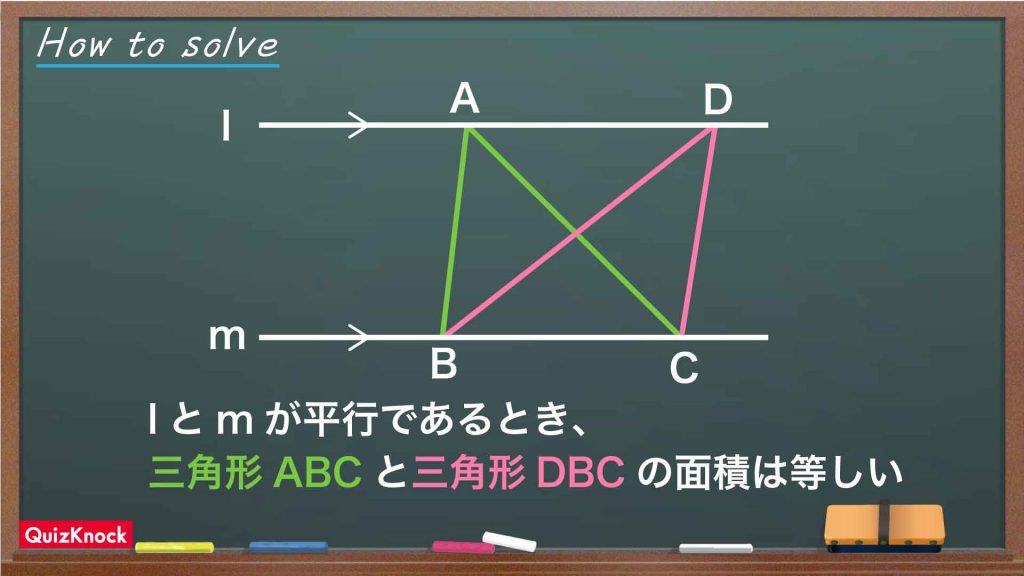
この性質を利用して、図形の面積を変えずにその図形を変形することを「等積変形」と呼びます。

三角形を変形する

下の図のように、長方形の対角線を引きます。このとき、青色の三角形と緑色の三角形において、直角を挟んでいる2つの辺の比はどちらも3:4であるため、2つの三角形は相似の関係にあります。したがって、青色の三角形と緑色の三角形の斜辺は平行です。

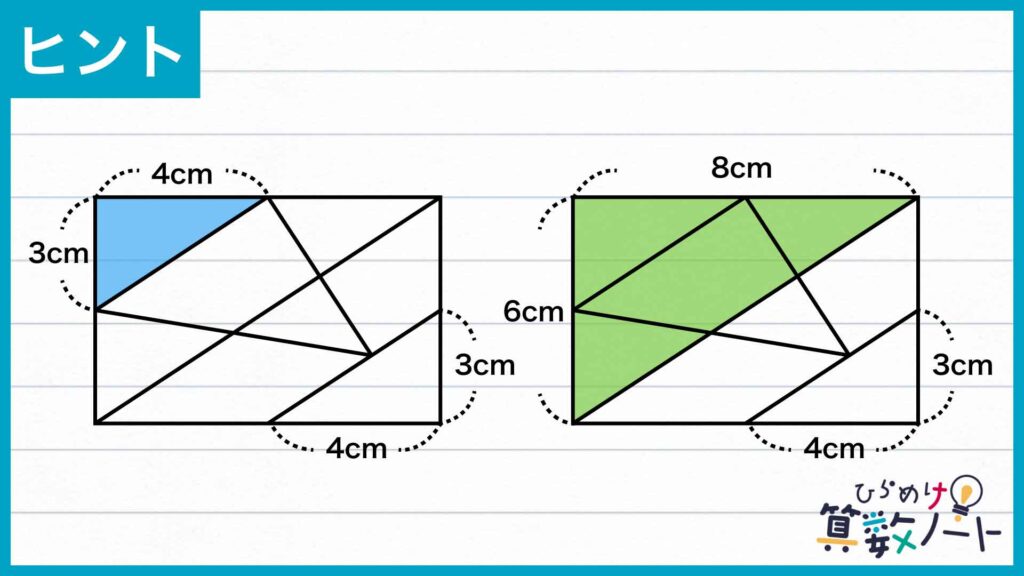
そのため、赤色の三角形は下の図のように等積変形することができます。

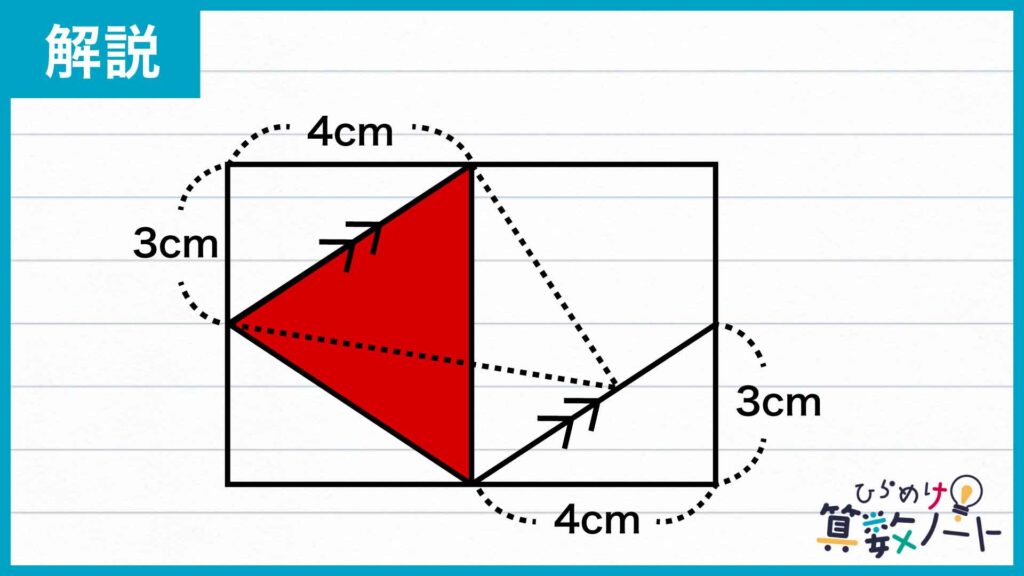
変形した三角形は、底辺が長方形の短い方の辺と平行で、その底辺の長さが6cm、高さが4cmです。したがって、面積は6×4÷2=12cm²となります。

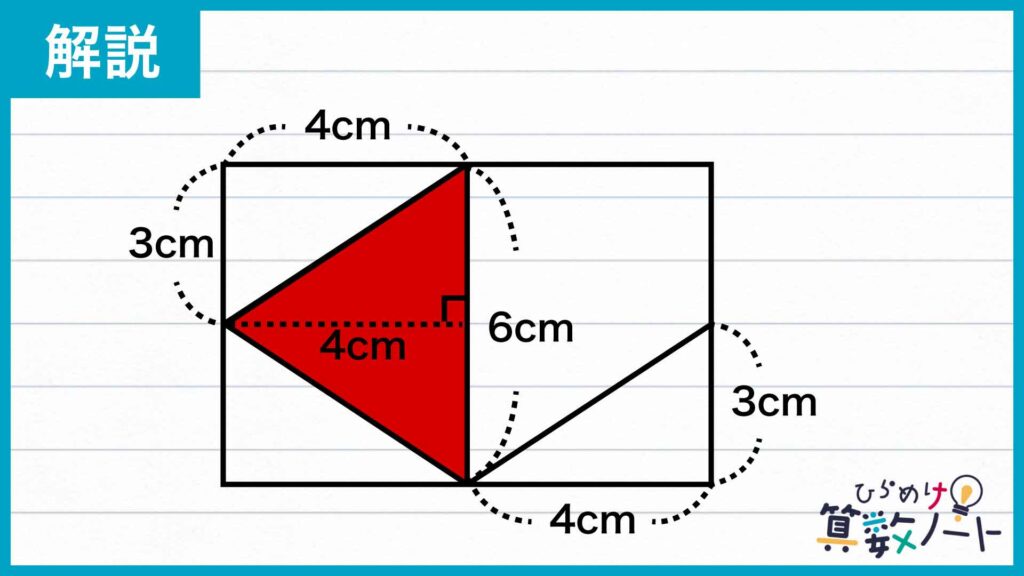
答え：12cm²

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】