ヒント
応用問題では、船が複数出てきたり途中でエンジンが止まったりと状況が複雑です。これらの情報をひとまとめに考えるのは大変なので、場面ごとに状況を整理してみましょう。ここでは、船Bのエンジンが止まるまでの流れを追ってみます。
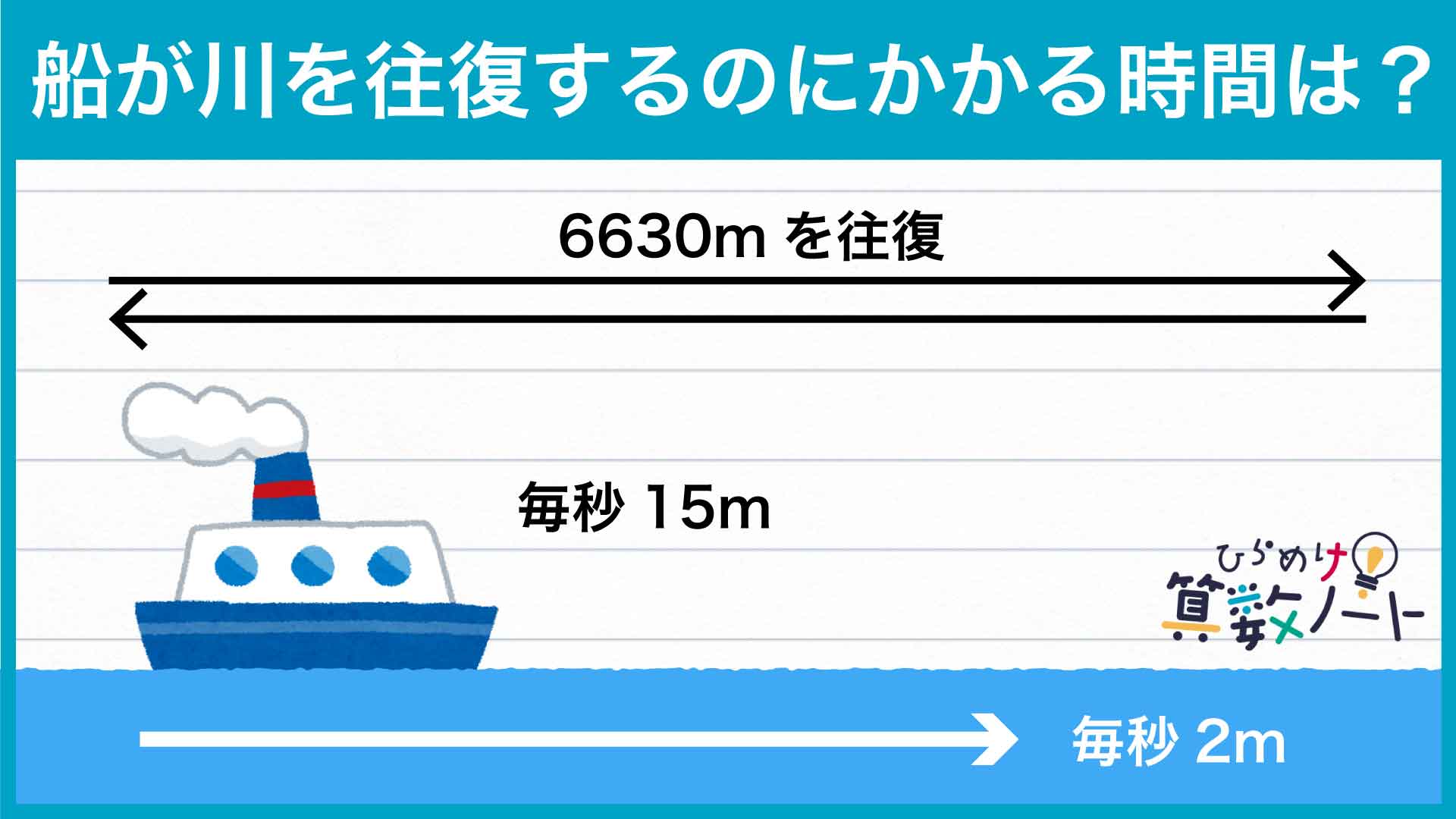
まず、スタート時の船A・Bの速さについて考えます。流れのない場所ではA・Bともに毎秒15mの速さで進みますが、この問題では川を進む向きによって速さに変化が生じます。流れに従って進むAは流速の分だけ速くなり、流れに逆らうBは同じだけ遅くなります。
よって、上の図のようにAの速さは15+2=毎秒17m、Bの速さは15-2=毎秒13mとなります。
Bは川の全長の3分の1、すなわち6630÷3=2210m進んだところでエンジンが停止したので、スタートしてからエンジン停止までの時間は2210÷13=170秒ということがわかりました。
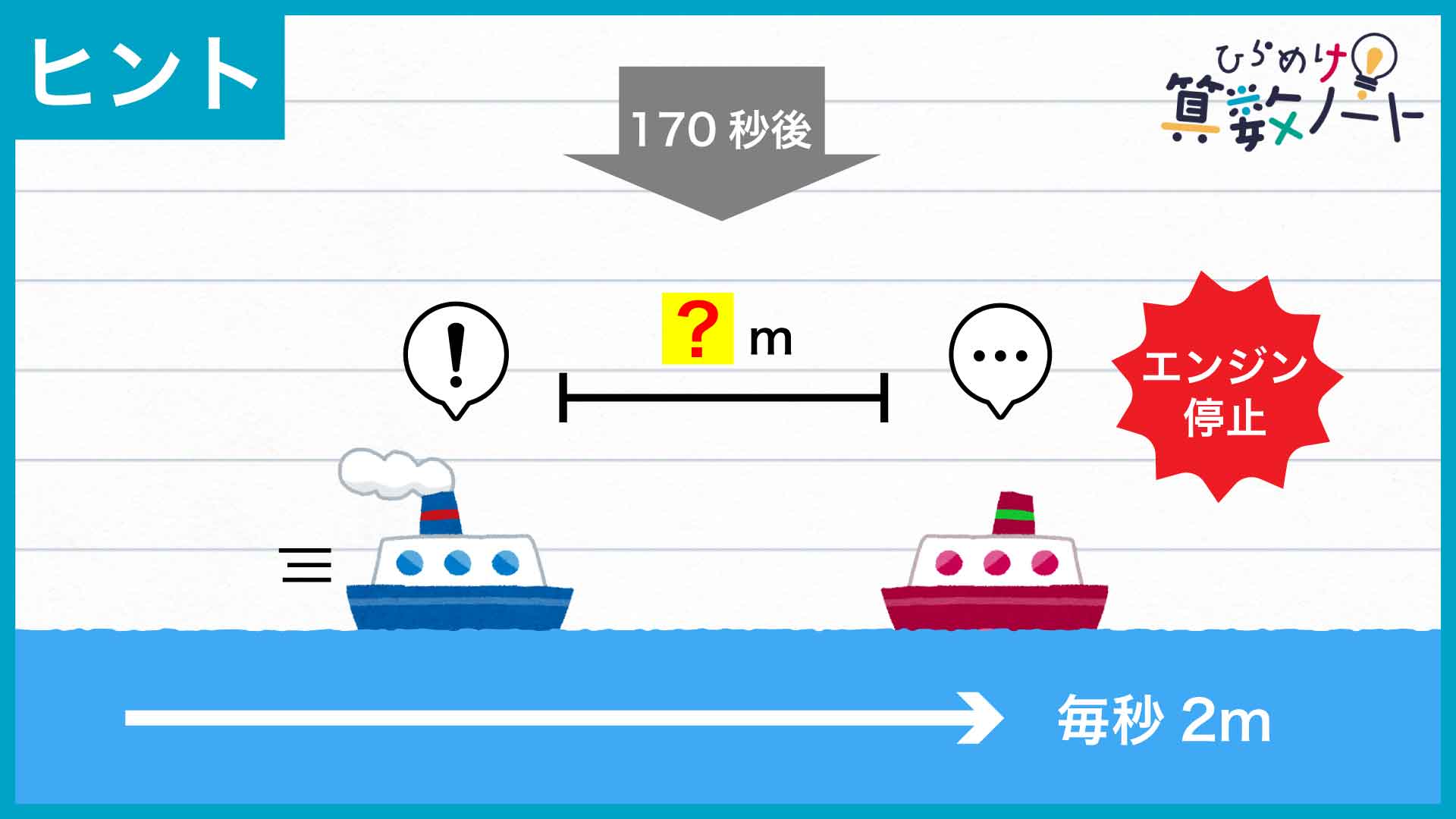
スタートから170秒後、Aは引き続き毎秒17mで川下へと向かいますが、Bの動きは大きく変化します。エンジン停止時のA・B間の距離を求めた上で、2つの船が「出会う」までの時間を考えてみましょう。

















.jpg)







