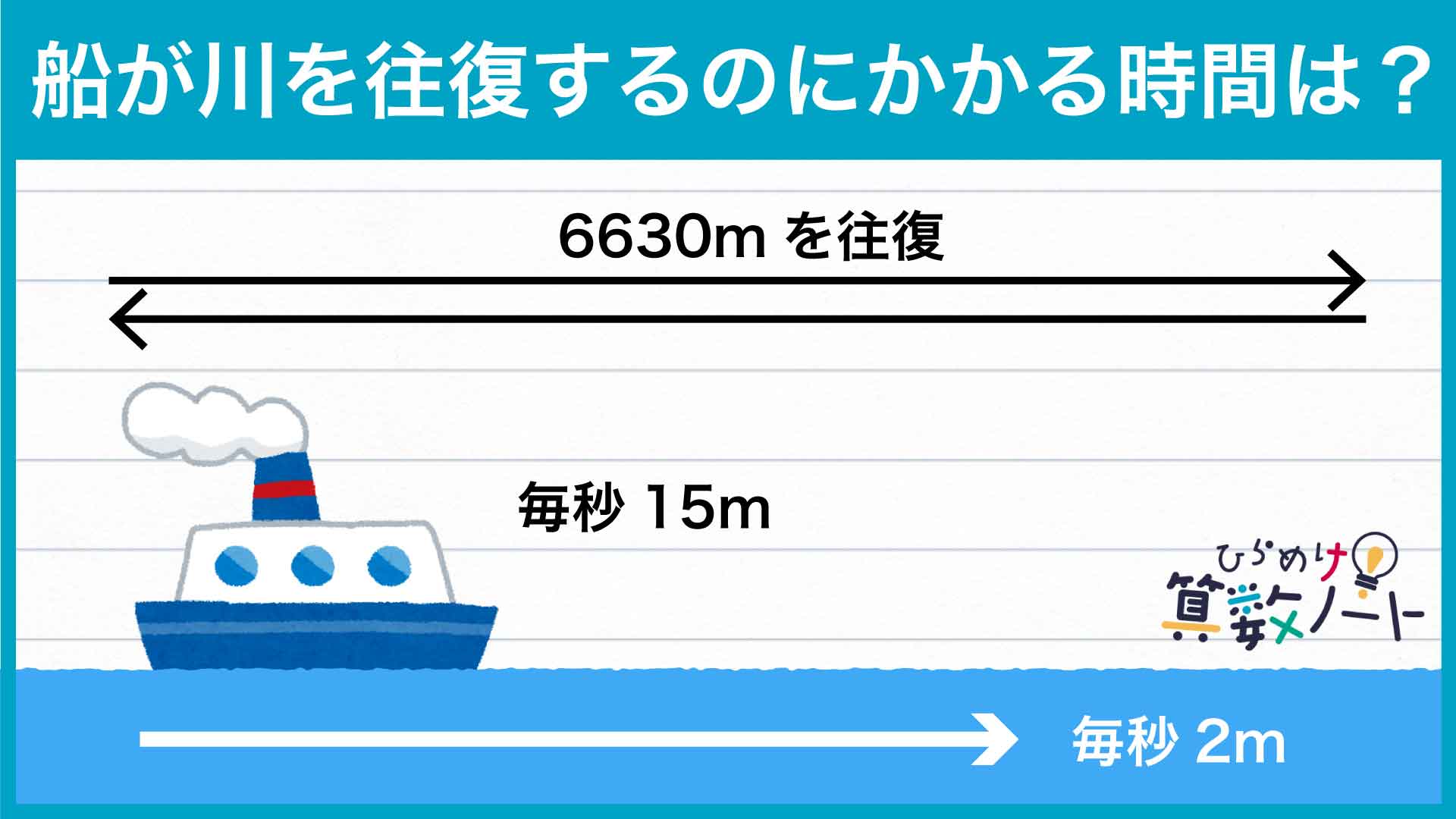
問題はこちら
2ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の解説です
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
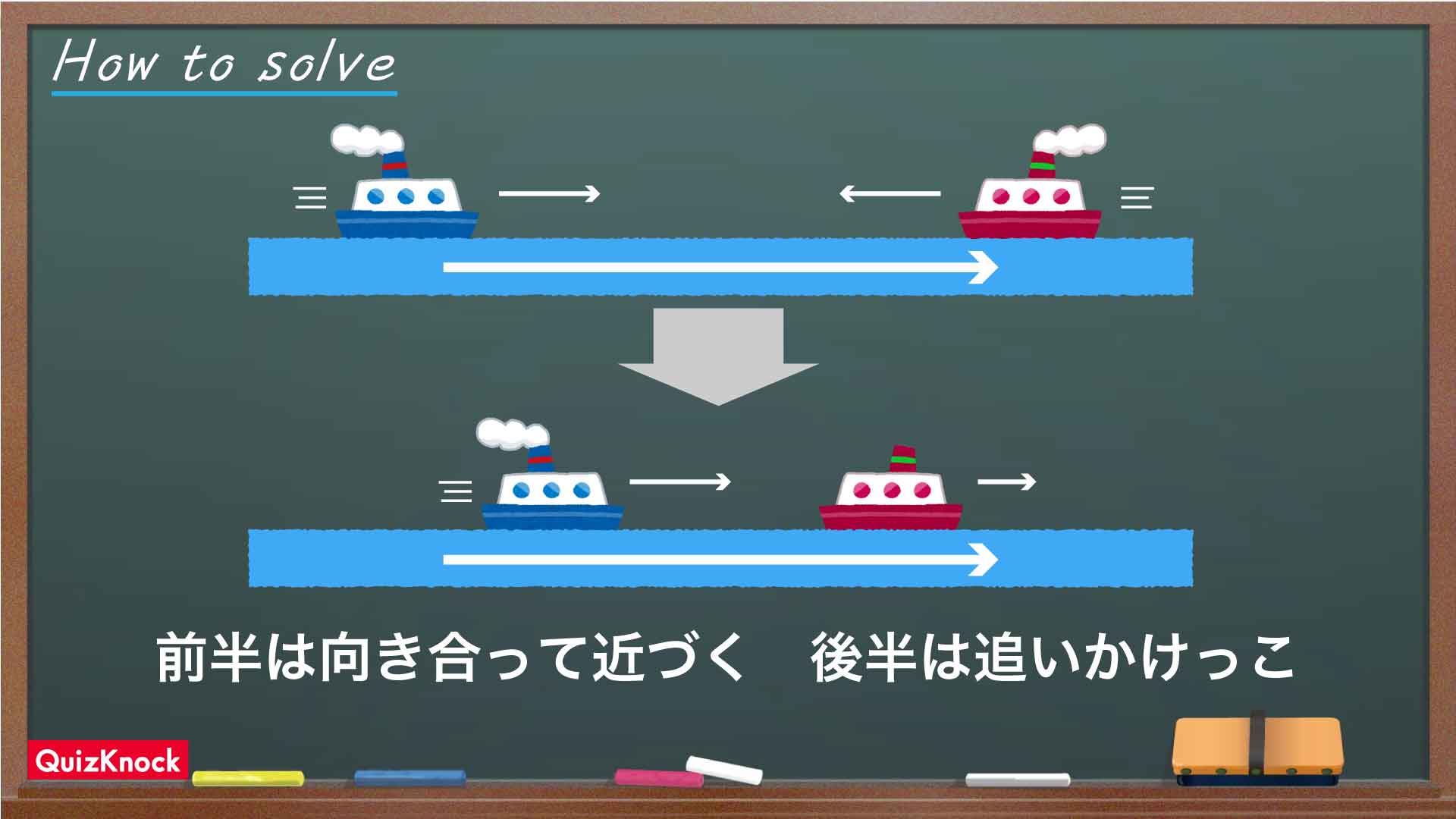
この問題の解き方をまとめた図がこちらです。
ポイントは、エンジンの停止前後で異なる船の動きをきちんと把握することです。
では、このポイントを踏まえつつ解いていきましょう!
スタート〜エンジン停止
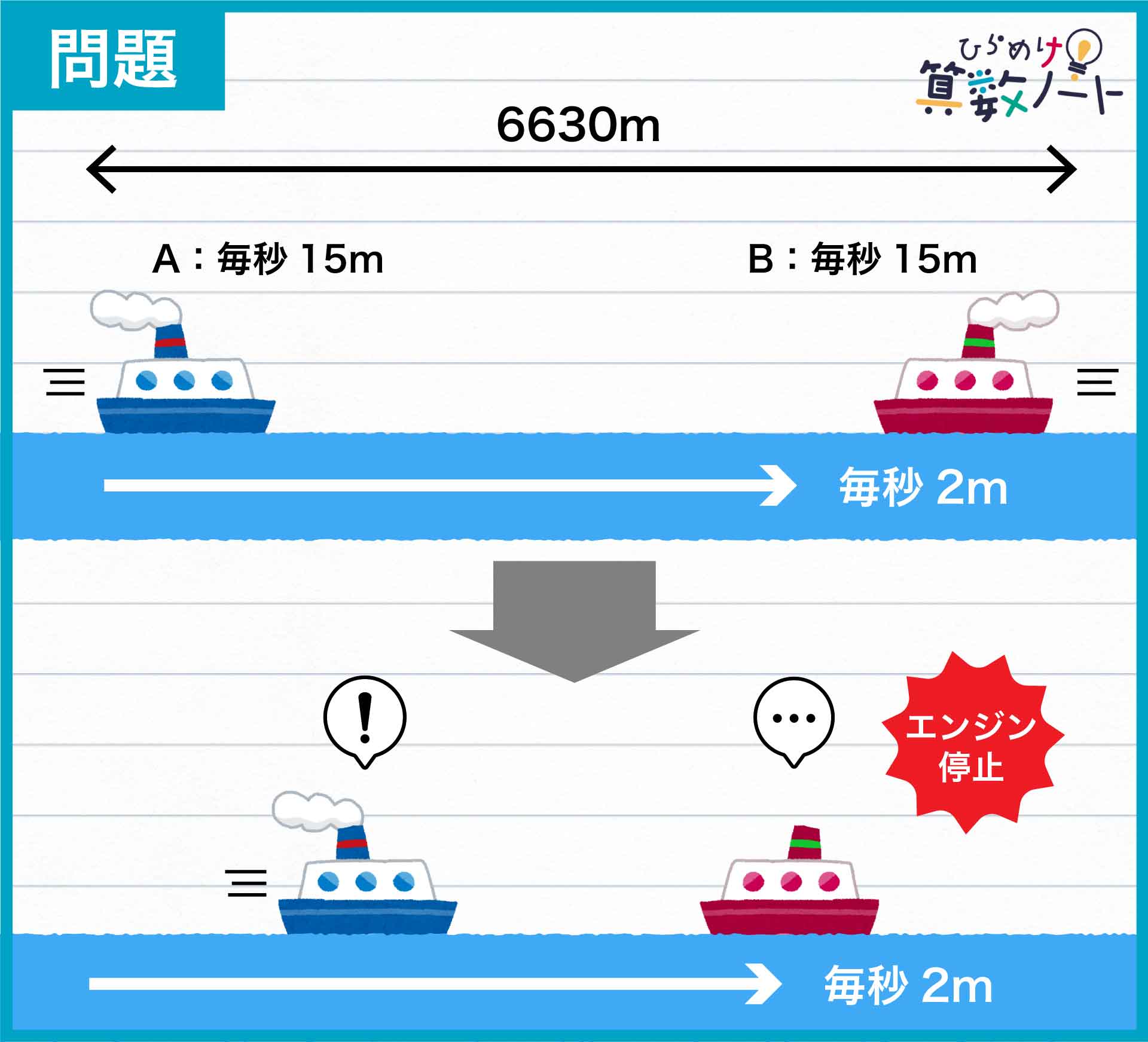
まずは、スタートしてからBのエンジンが停止するまでの船の動きを考えます。
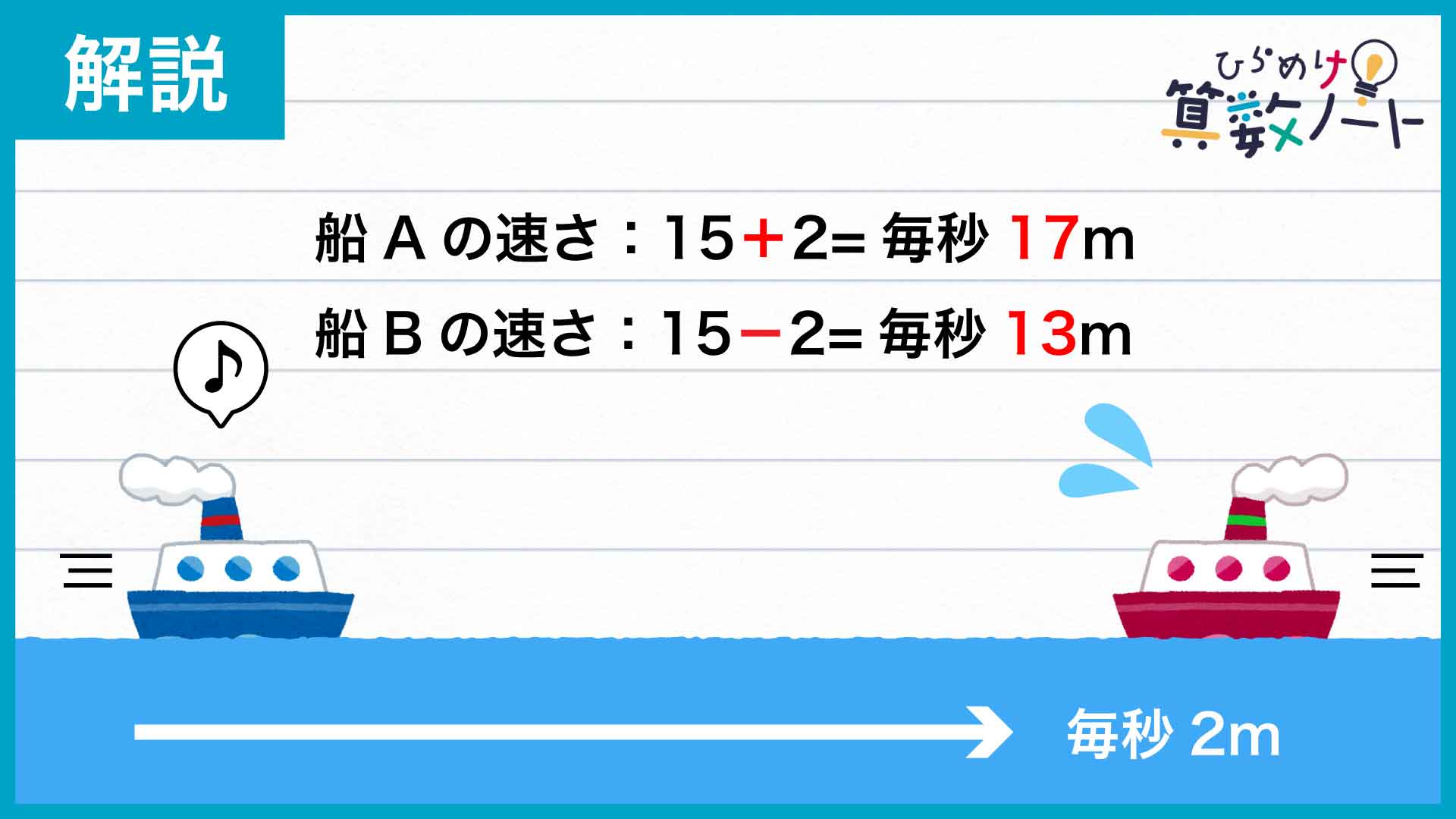
ウォーミングアップの解説にもあったように、流れに従って進む船は川の流速の分だけ速く、逆に流れに逆らって進む船は川の流速の分だけ遅くなります。よって、川下へ向かうAの速さは15+2=毎秒17m、川上へ向かうBの速さは15-2=毎秒13mとなります。
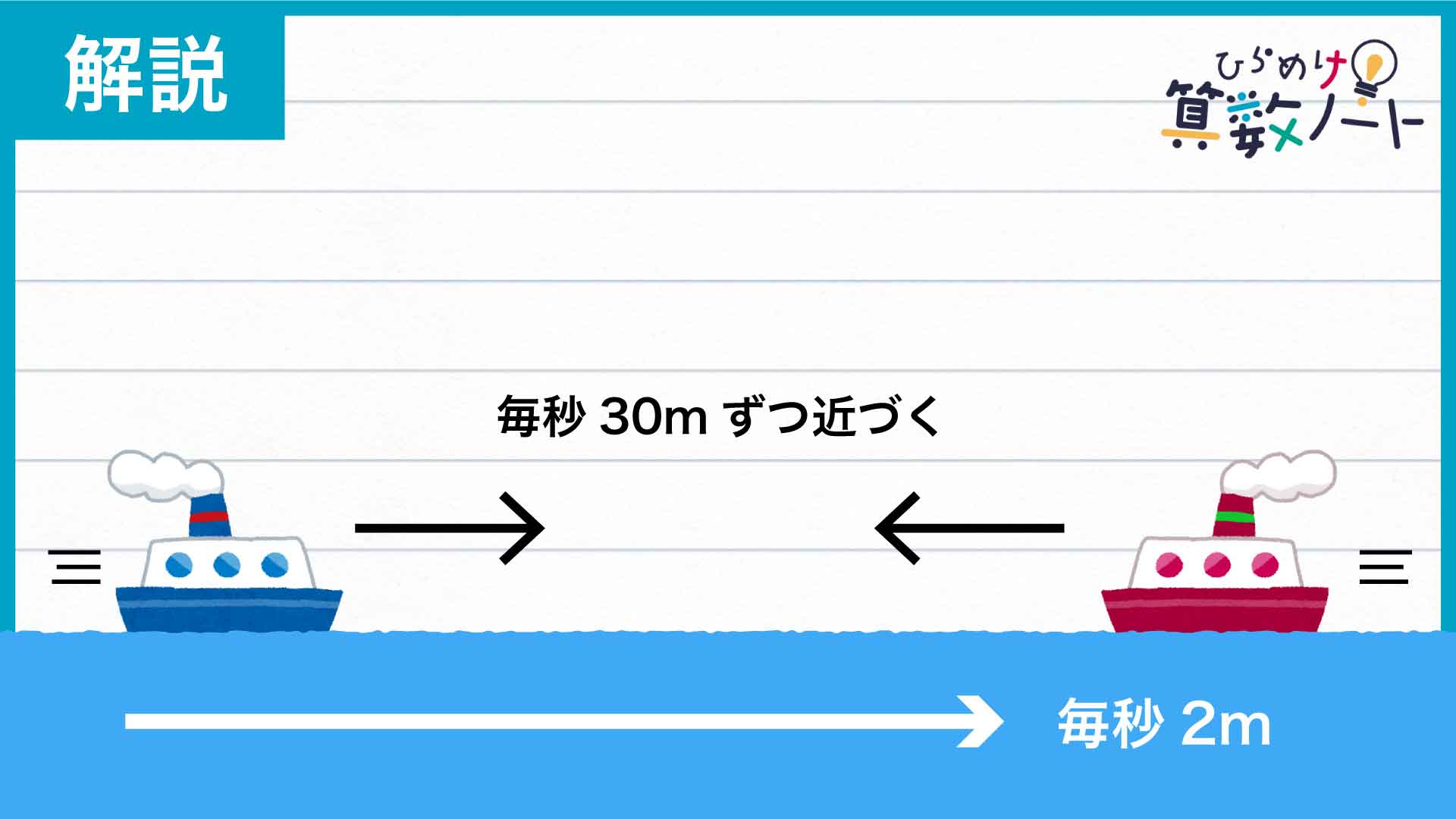
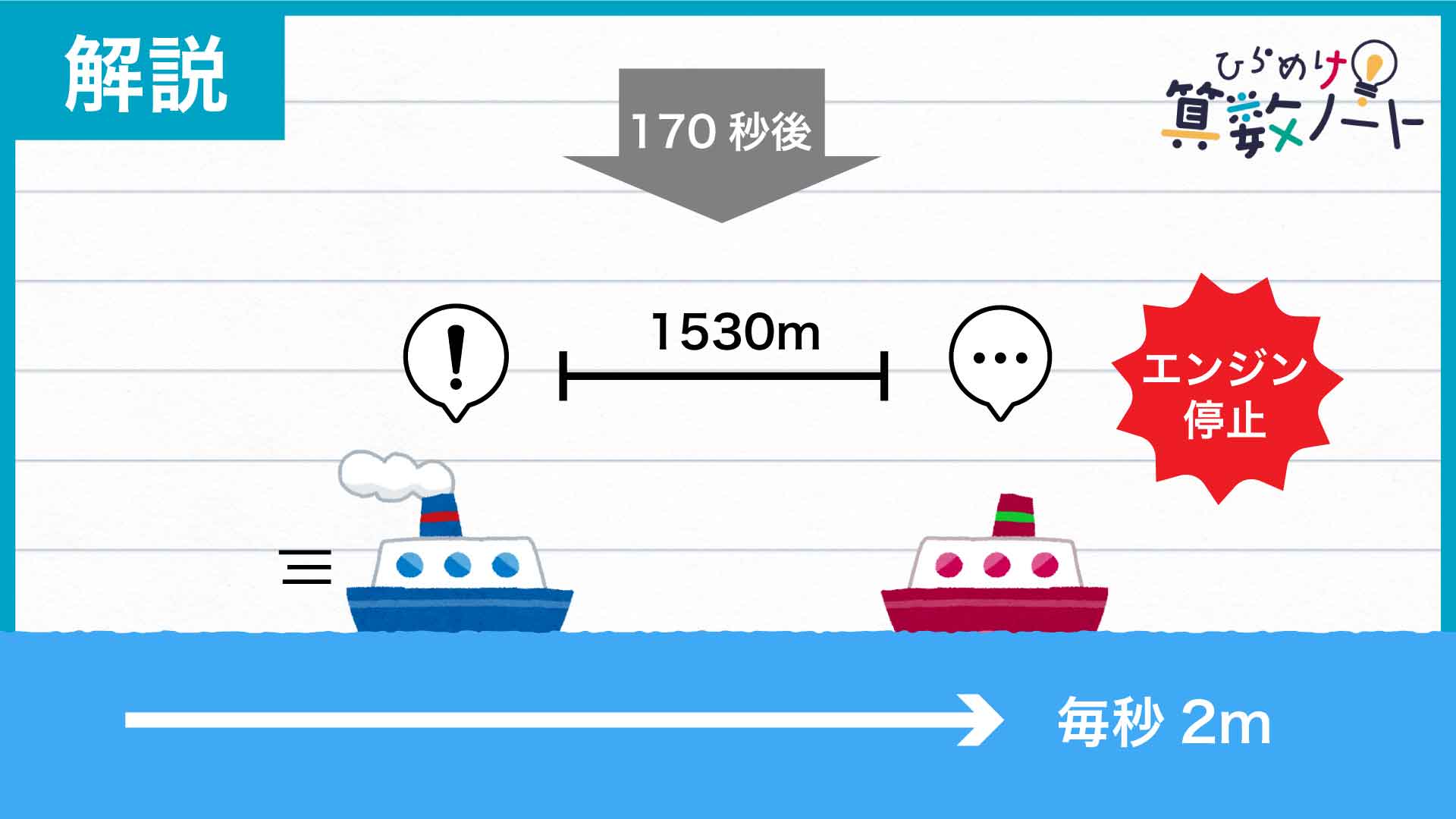
Bは川の全長の3分の1、すなわち6630÷3=2210m進んだところでエンジンが停止します。このとき、スタートから経過した時間は2210÷13=170秒なので、AとBの距離は向き合って170秒進んだ分だけ短くなっているはずです。
両者の間の距離は1秒間に17+13=30mずつ短くなるので、Bのエンジンが停止した瞬間のAとBの間の距離は6630-30×170=1530mであることがわかりました。
エンジン停止〜AとBが出会うまで
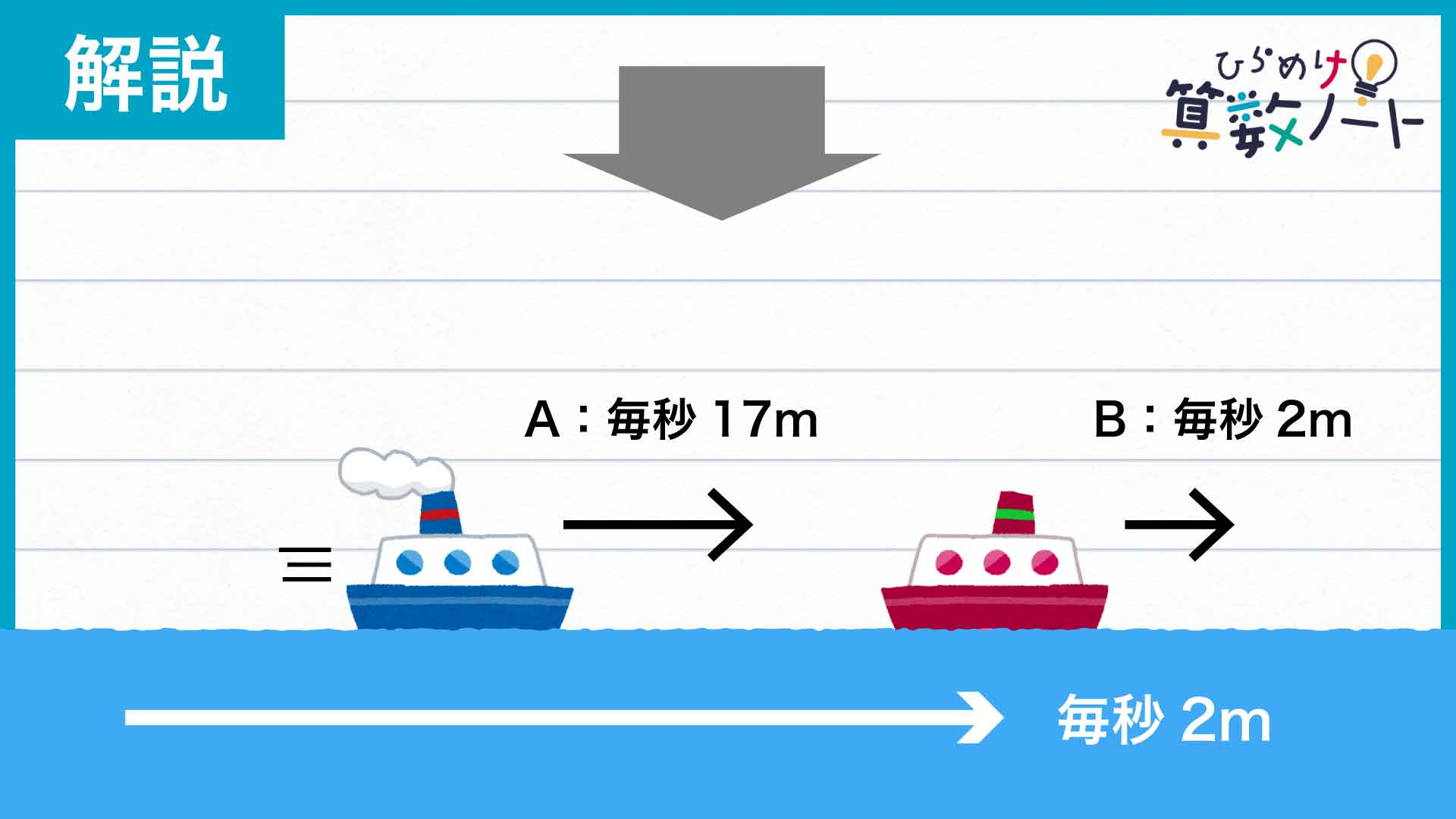
Bのエンジンが停止した後、Aは変わらず毎秒17mで川下に向かって動き続けます。一方、エンジンが止まったBはただ川に流されることになるので、川下へ毎秒2mで押し戻されてしまうのです。
したがって、エンジンの停止後は川下へ流されるBをAが追いかけるような動きに変わります。エンジン停止直後のBはAより1530m川下側におり、両者の距離は1秒間に17-2=15mずつ縮まります。よって、エンジンが停止してからAがBに追いつくまでの時間は1530÷15=102秒とわかるのです。
以上のことから、AとBがスタートしてから出会うまでにかかる時間の合計は、スタートからエンジン停止までの時間と、エンジン停止からAとBが出会うまでの時間を合計して、170+102=272秒となります。
答え:272秒
「ひらめけ!算数ノート」のバックナンバーはこちら!
【前回の算数ノートはこちら】
【あわせて読みたい】









.jpg)










.jpg)







