問題はこちら
前ページ:【解答フォーム】自力で解きたい方はこちらへ! 以下は問題の答えです
解説
それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。
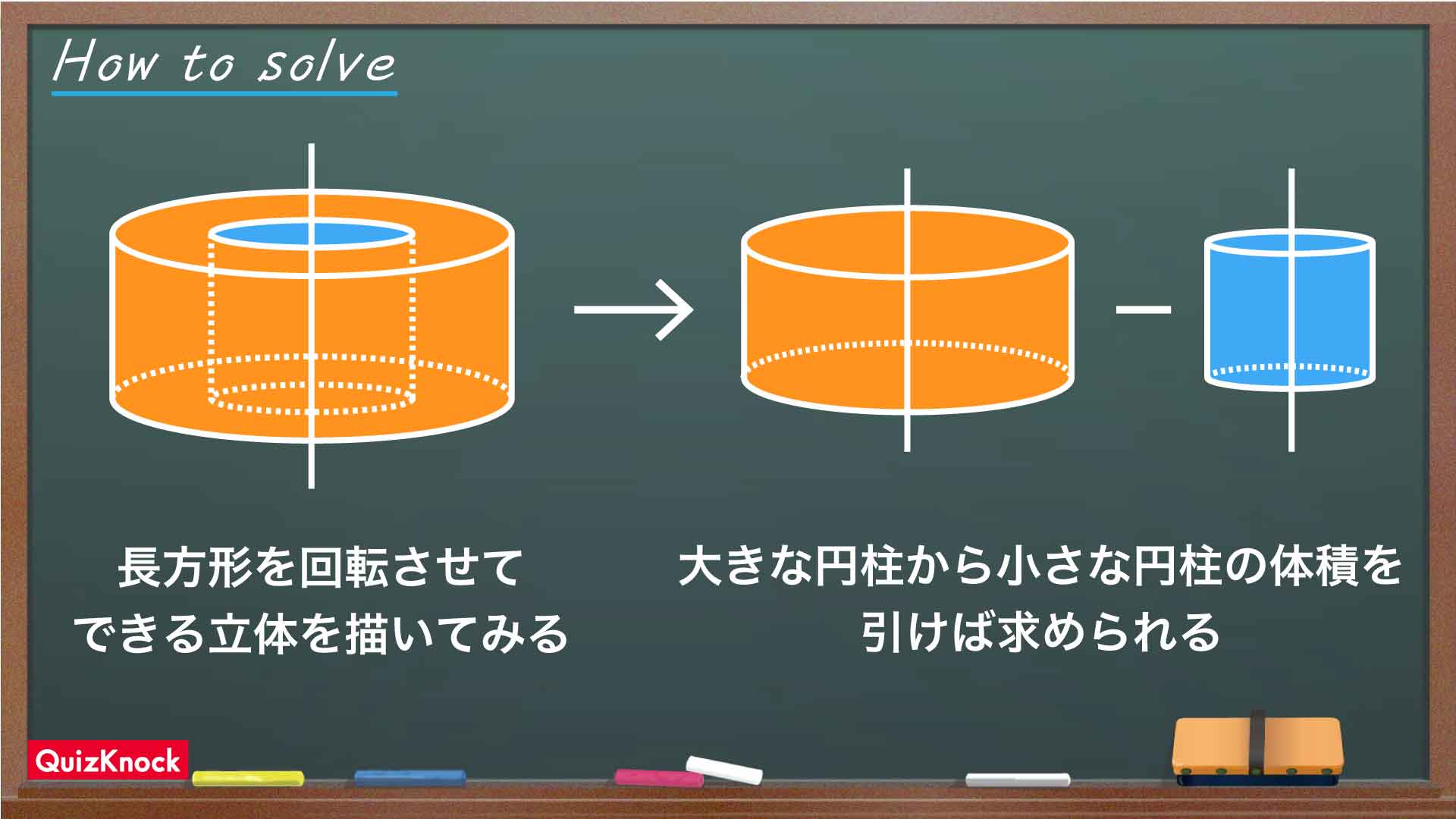
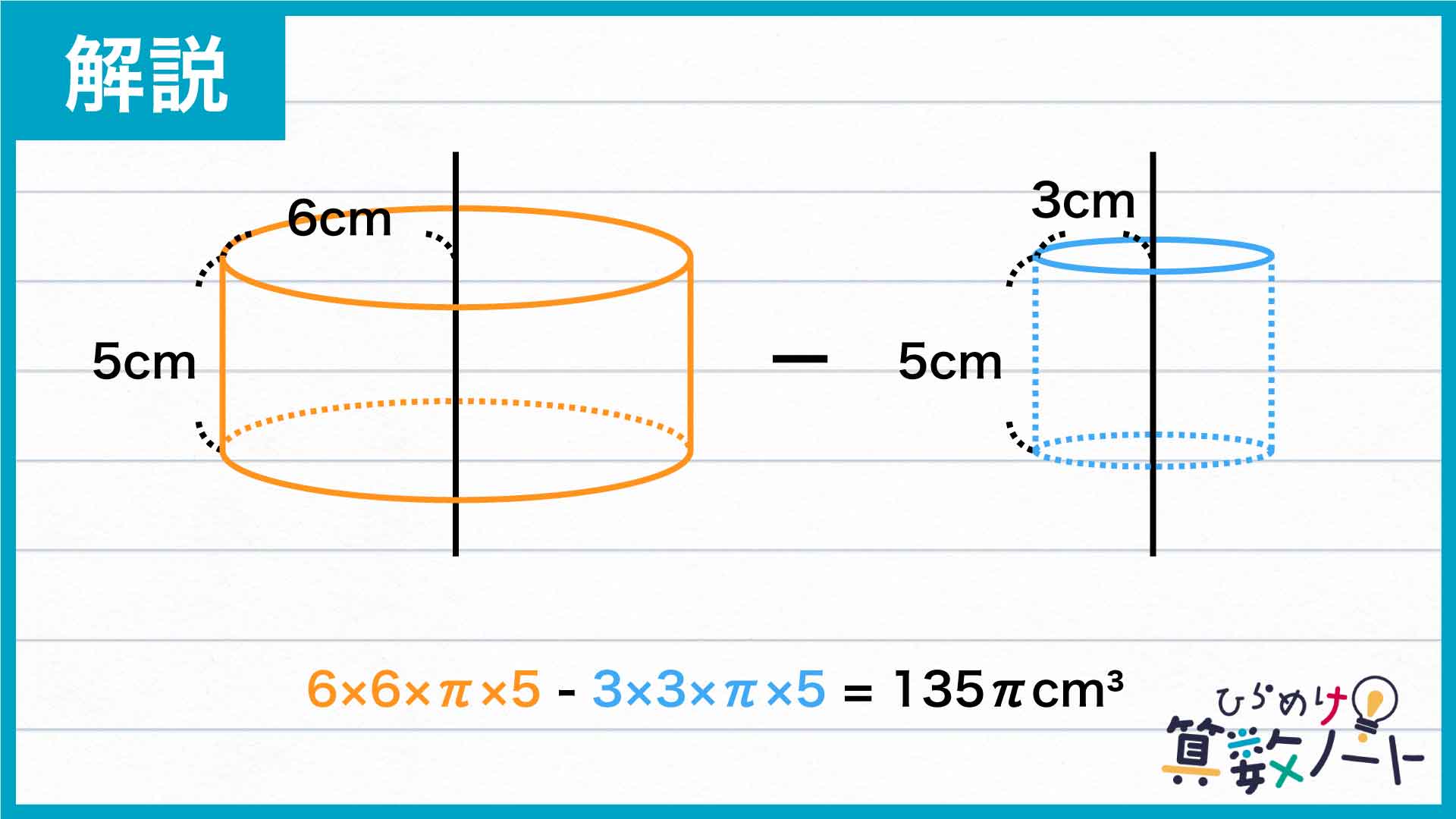
今回の解き方をまとめた図がこちらです。
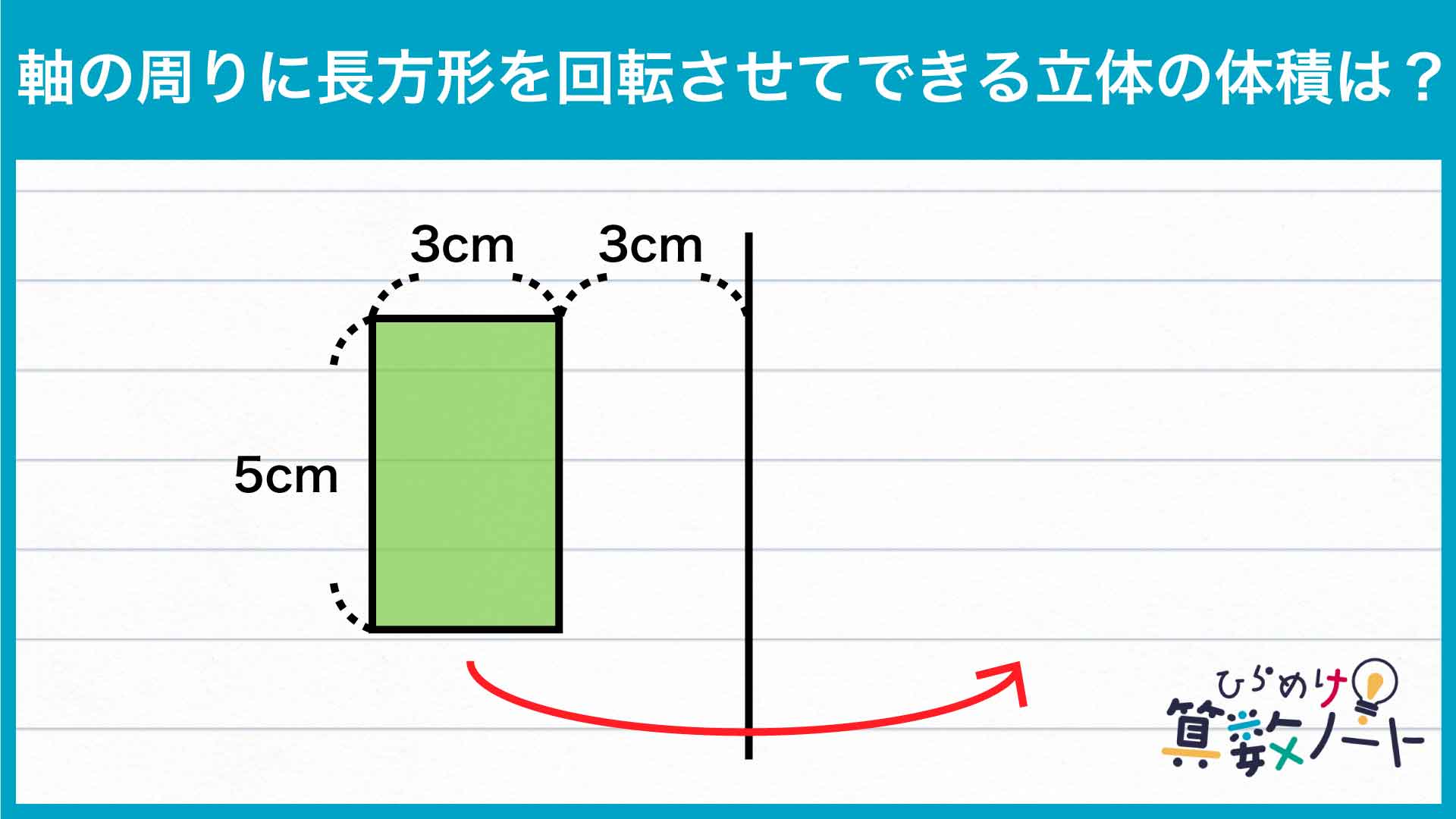
今回のポイントは、「長方形を回転させてできる立体を正確に把握する」ことです。
このポイントをもとに、問題を攻略していきましょう!
立体を描いてみる
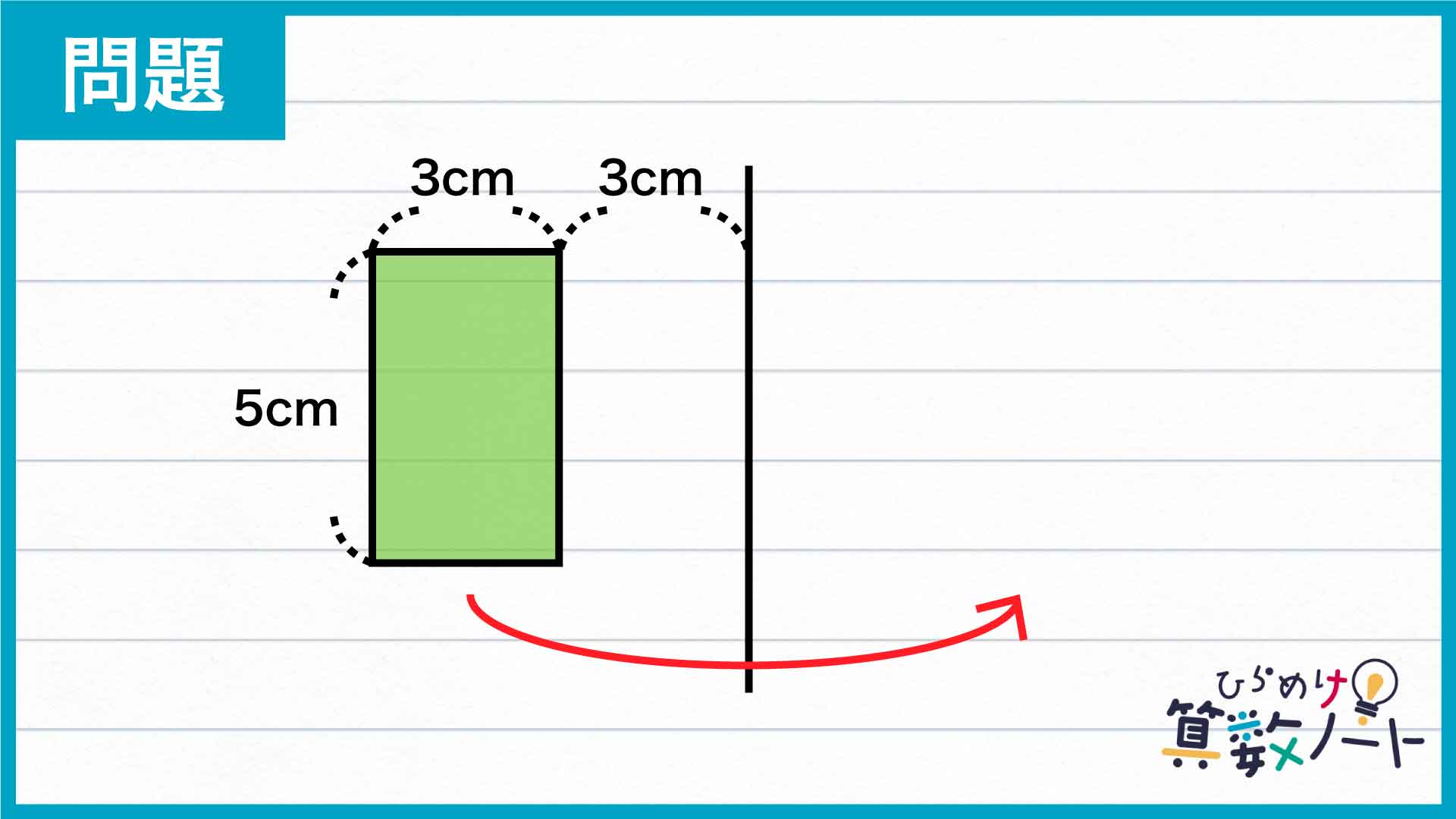
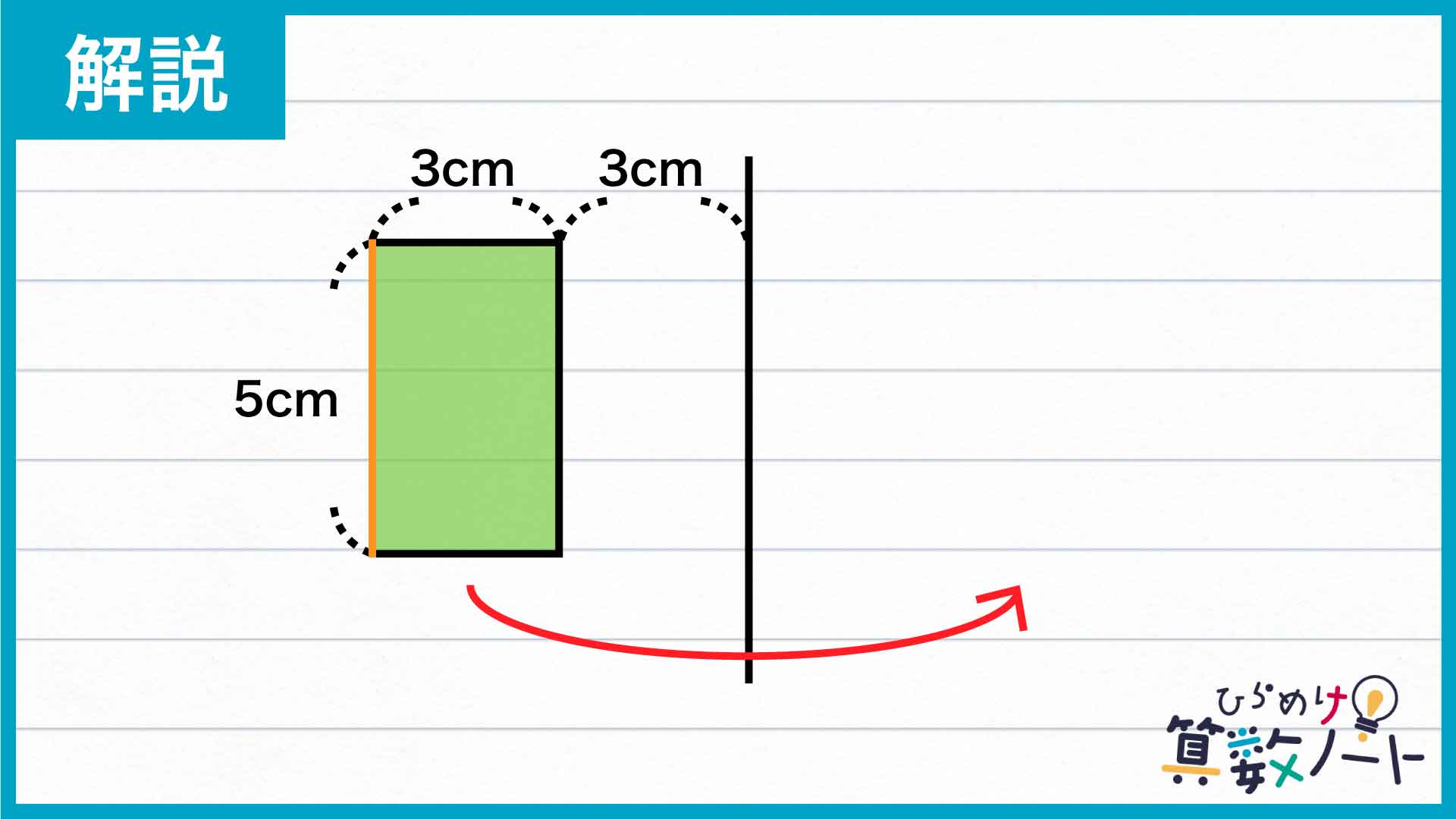
はじめに、長方形を軸の周りに回転させてできる立体がどのようになるかを考えます。
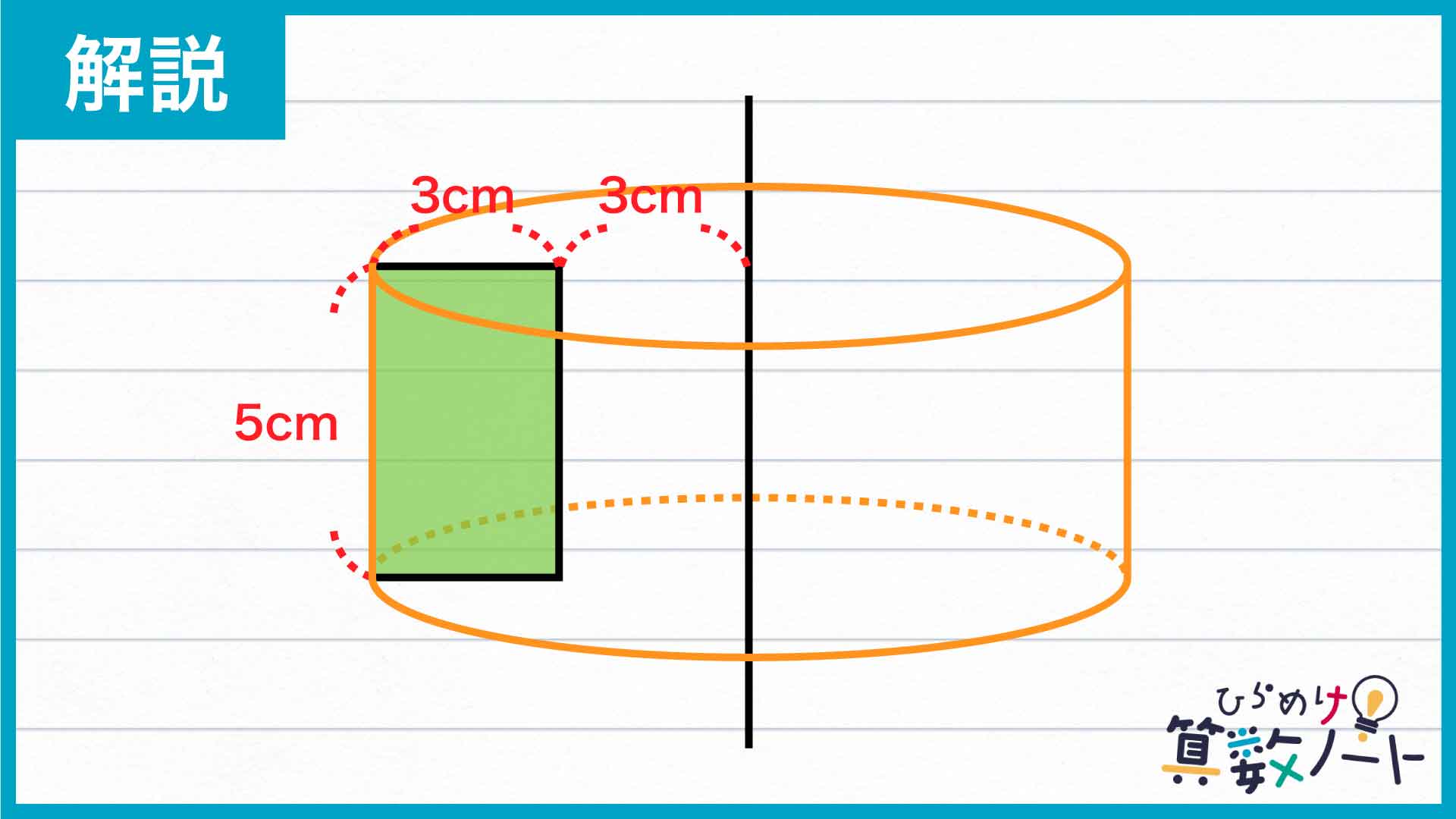
まずは下の図にオレンジ色で示した、軸と平行で、軸から遠い方の長方形の辺に注目します。
この辺を軸の周りに回転させてできる立体は、下の図のような半径が6cm、高さが5cmの円柱になります。
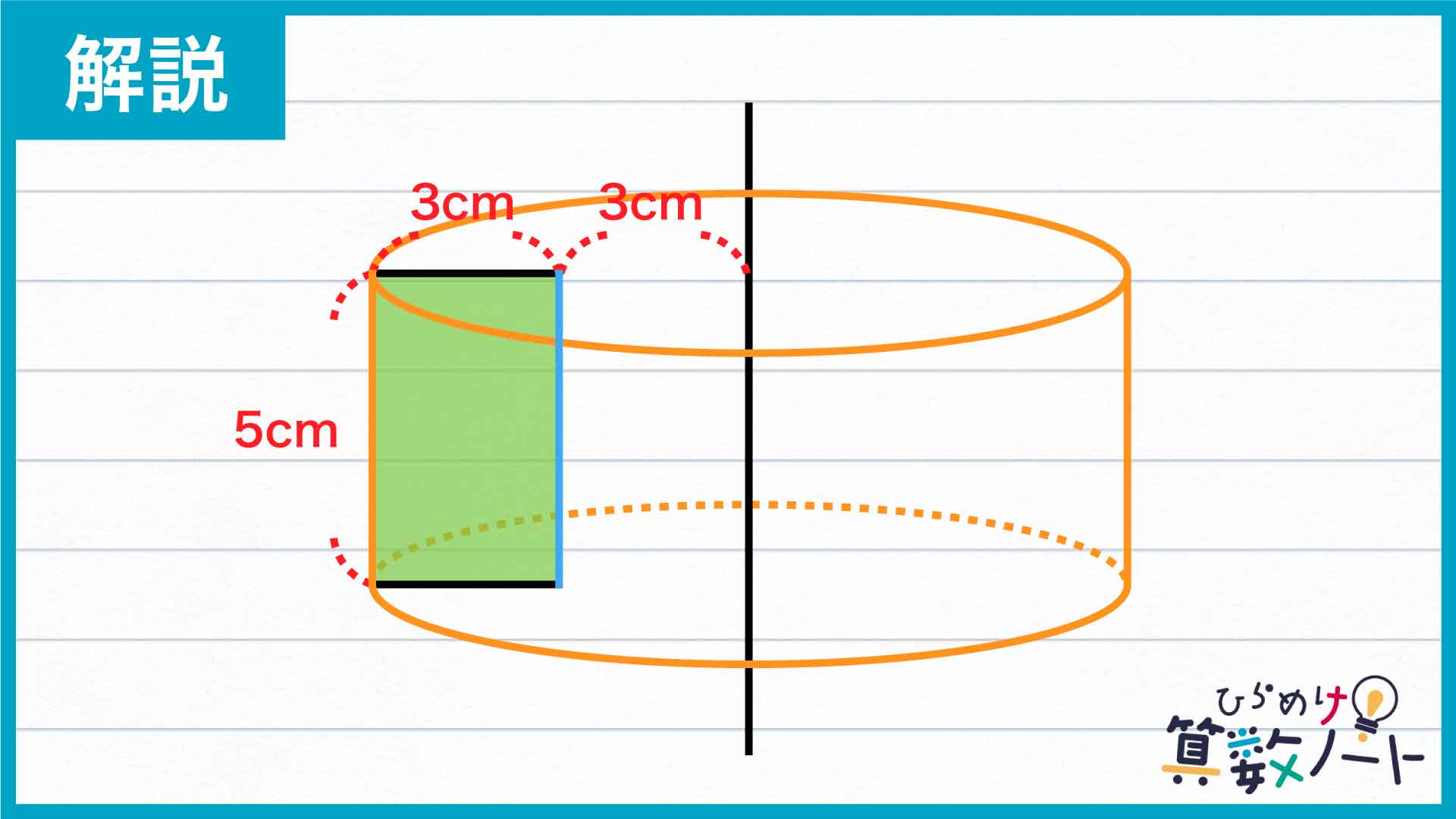
続いて、下の図に青色で示した辺に注目します。
この辺を軸に周りに回転させてできる立体は、半径が3cm、高さが5cmの円柱になります。
体積を求める
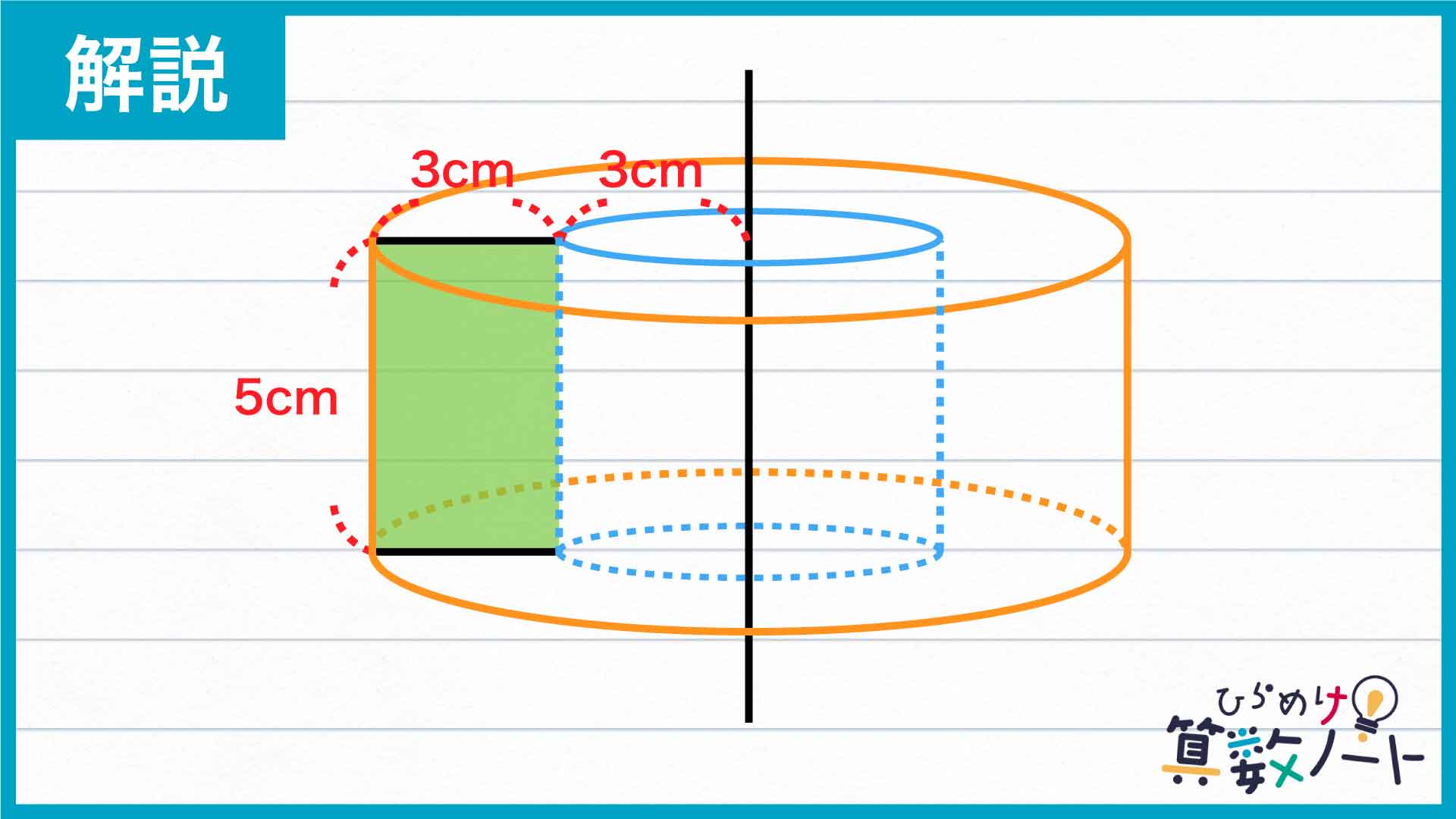
長方形を軸の周りに回転させてできる立体は、大きな円柱の中を小さな円柱が貫通したような立体になることがわかりました。
したがって、求める体積は(6×6×π×5)-(3×3×π×5)=135πcm3となります。
答え:135πcm3
それではまた次の算数ノートでお会いしましょう!
「ひらめけ!算数ノート」のバックナンバーはこちらから!
【前回の算数ノートはこちら】
【あわせて読みたい】










.jpg)









.jpg)






