小学生でも解ける「六角形の面積」の問題。あなたは解けますか？

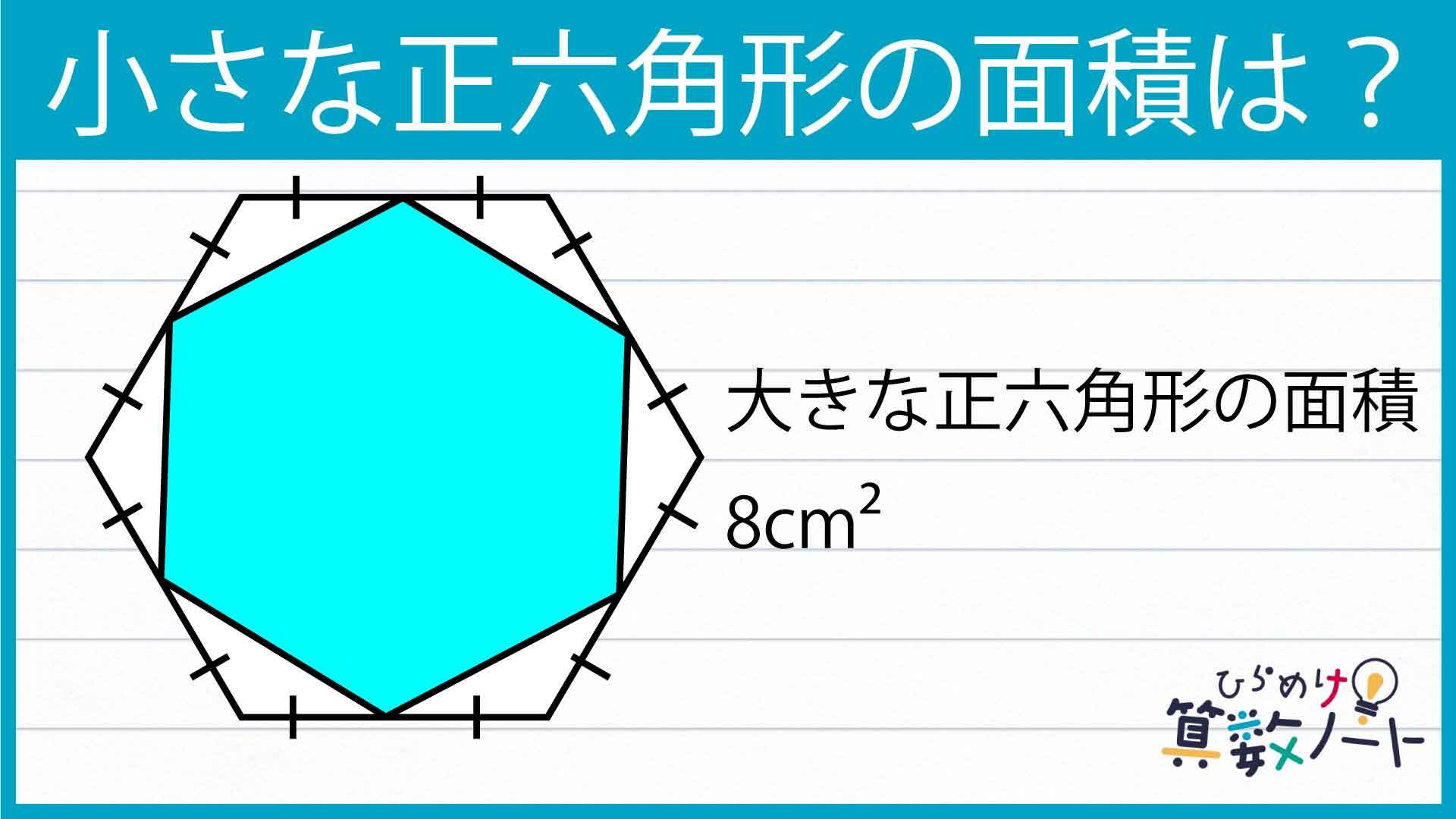
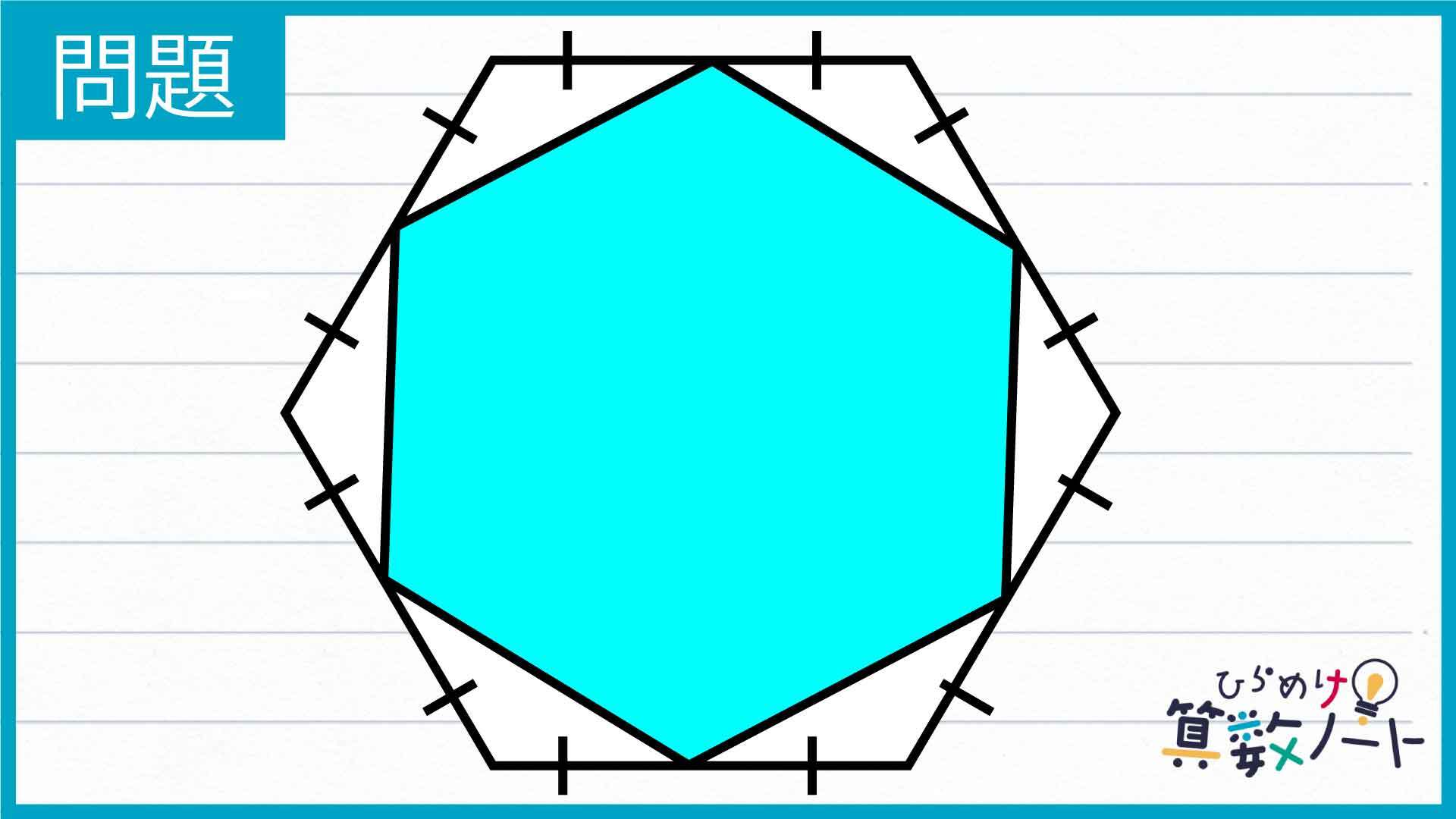
問題はこちら

前ページ：自力で解きたい方はこちらへ！以下は問題の解説です

解説

それでは解説です。さまざまな解き方がありますが、ここではそのひとつを紹介します。

今回の問題を解くうえで重要なポイントを以下にまとめました。

整理すると、

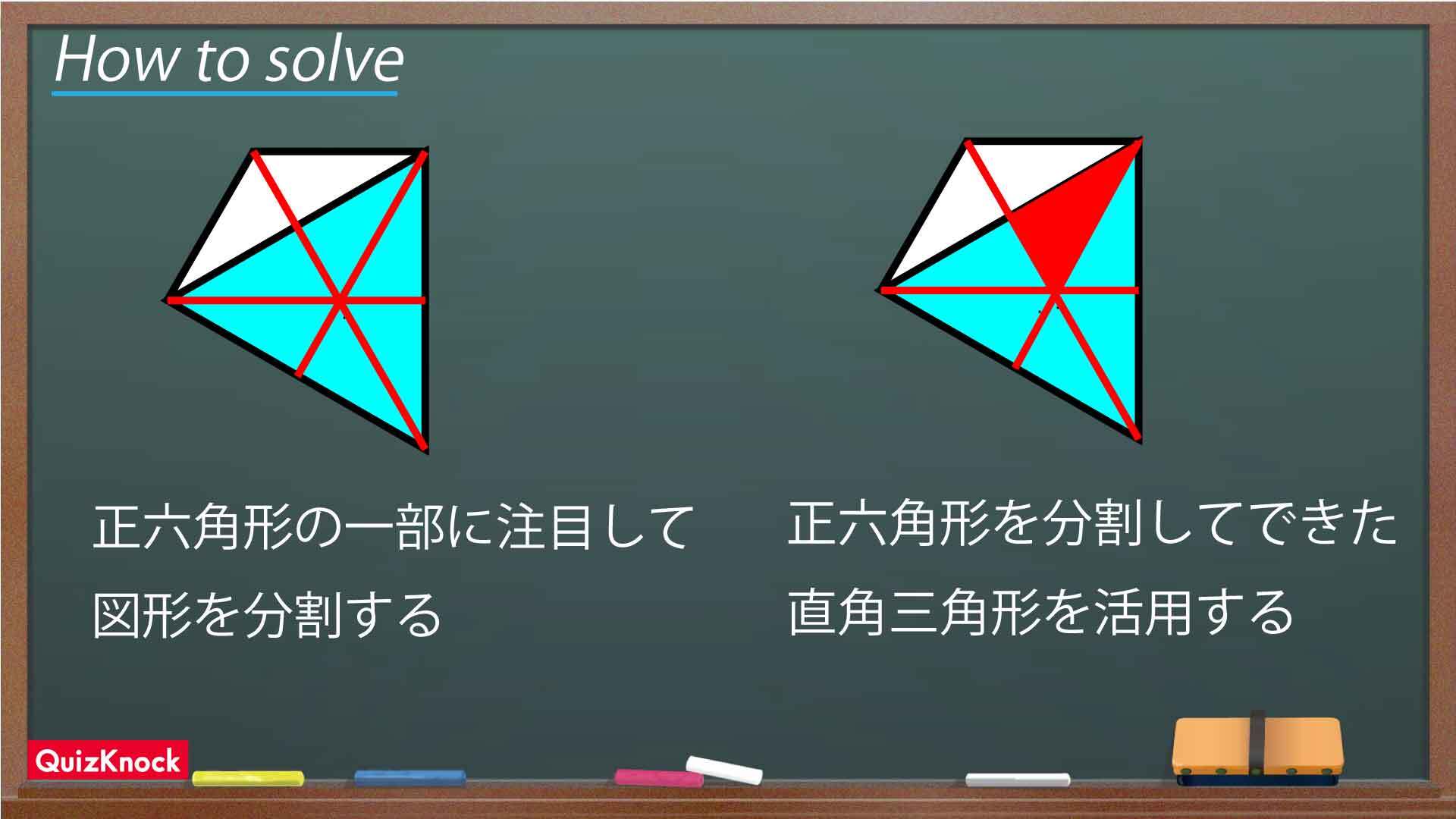
• 正六角形の一部に注目し、図形を分割する
• 正六角形を分割してできた直角三角形を活用する

の2点です。これらのポイントを踏まえながら、問題を解いていきましょう。

正六角形の一部に注目し、図形を分割する

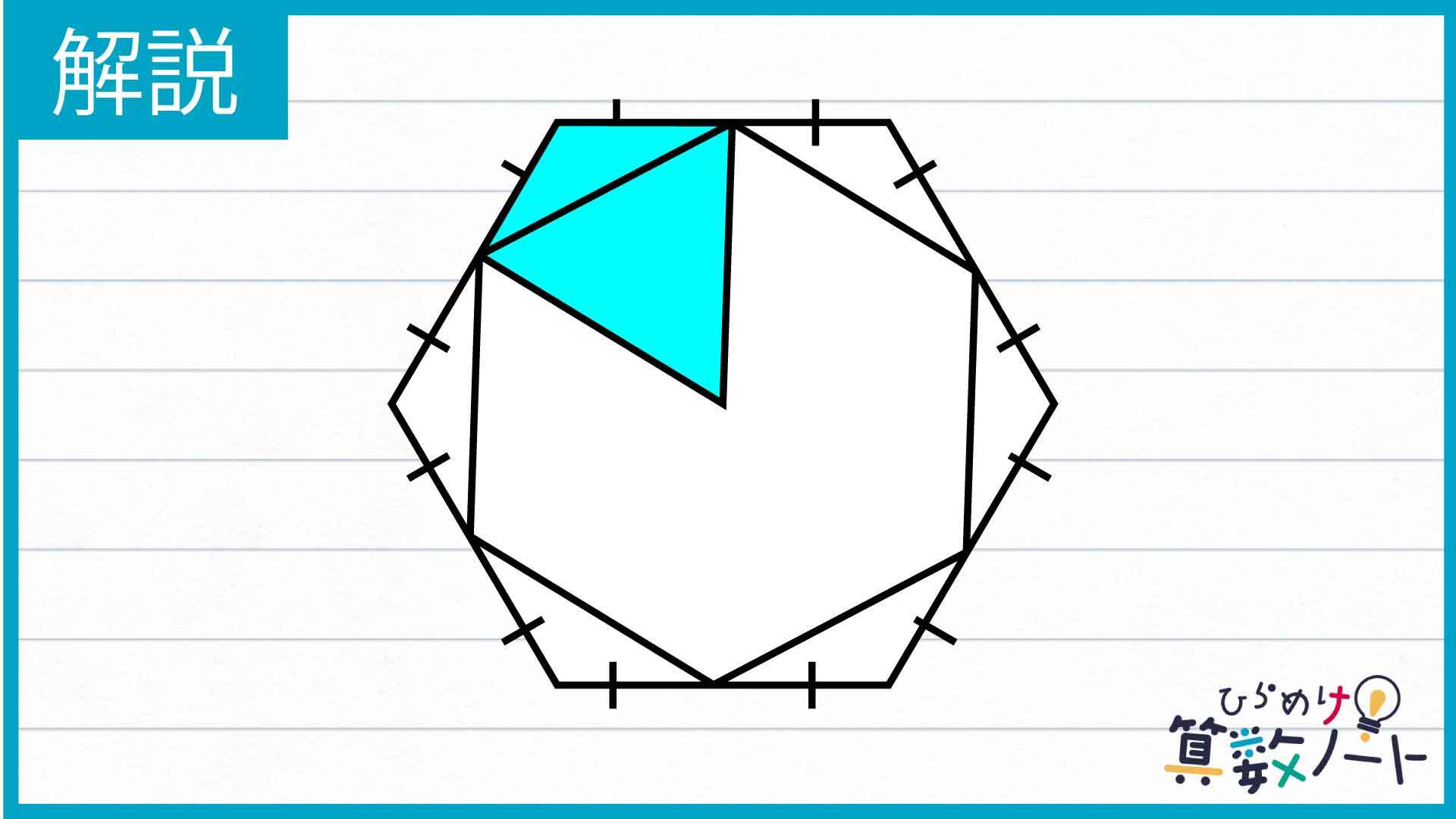
下の図で色を塗った部分の図形に注目しましょう。

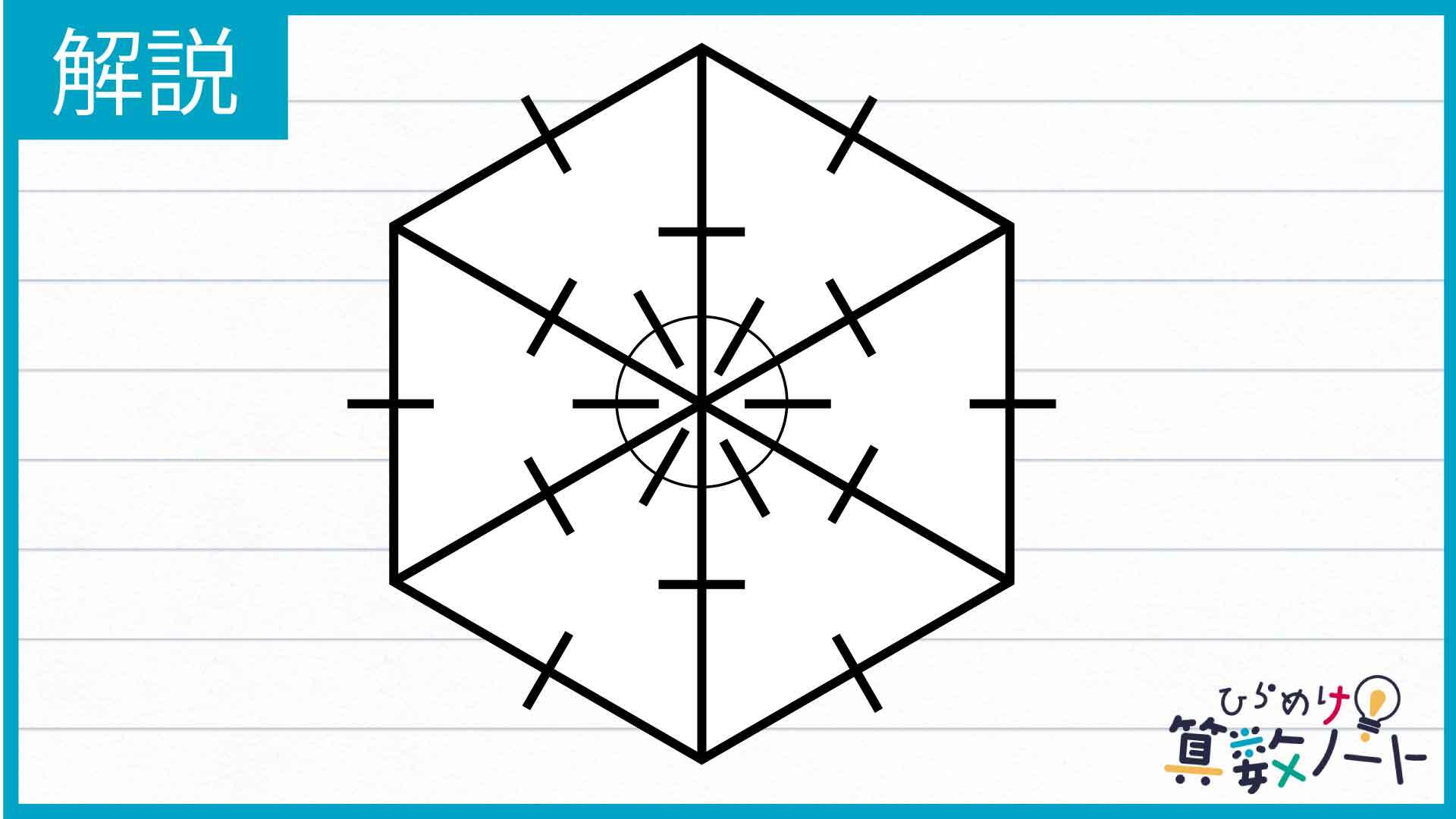
以下の図のように小さい方の正六角形を6等分したとき、中心の角も6等分され、360÷6=60度の角が6つできます。

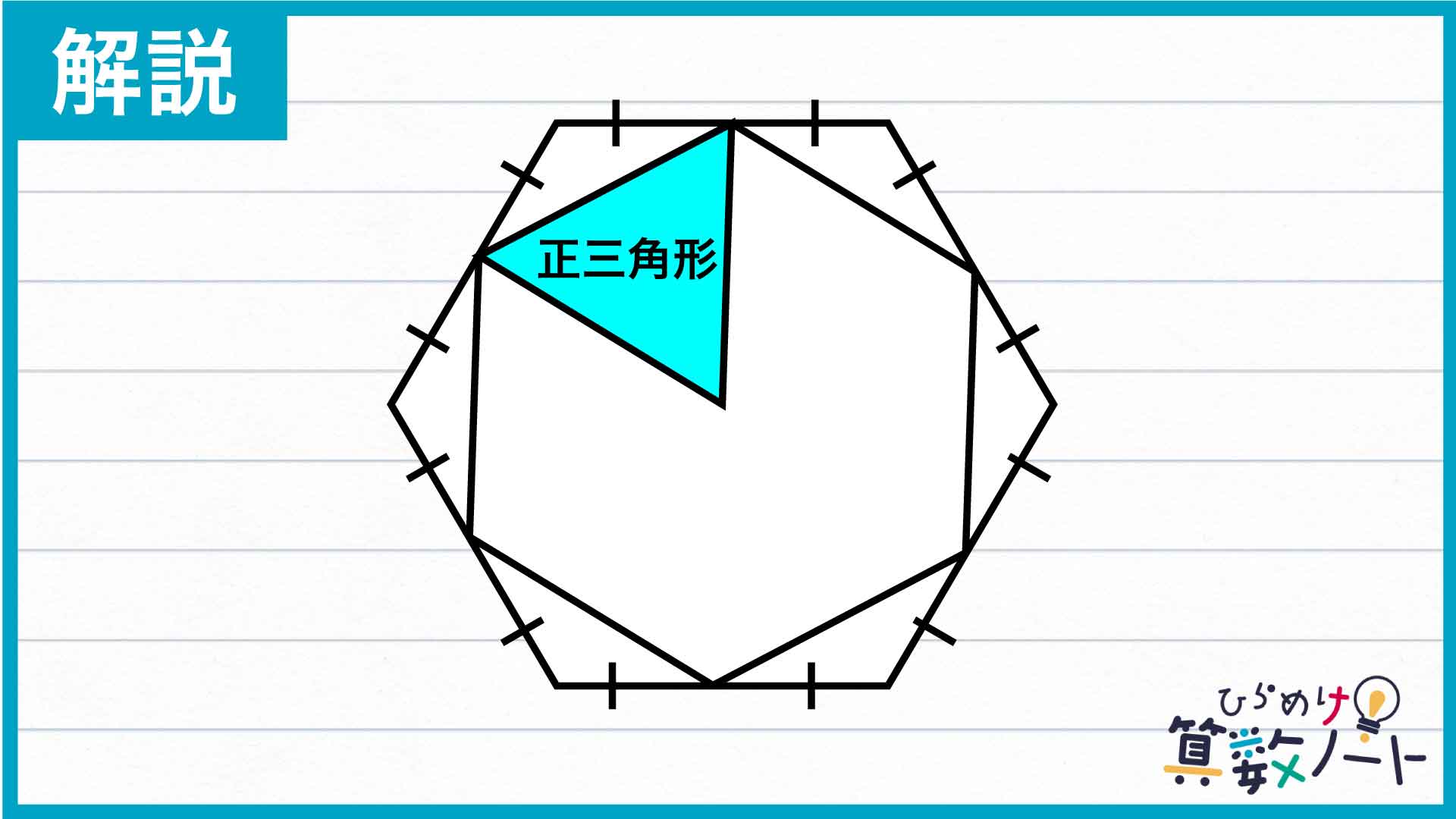
この60度の角をつくる線分の長さはそれぞれ等しいので、下の図の青い三角形は頂角が60度の二等辺三角形、つまり正三角形になります。

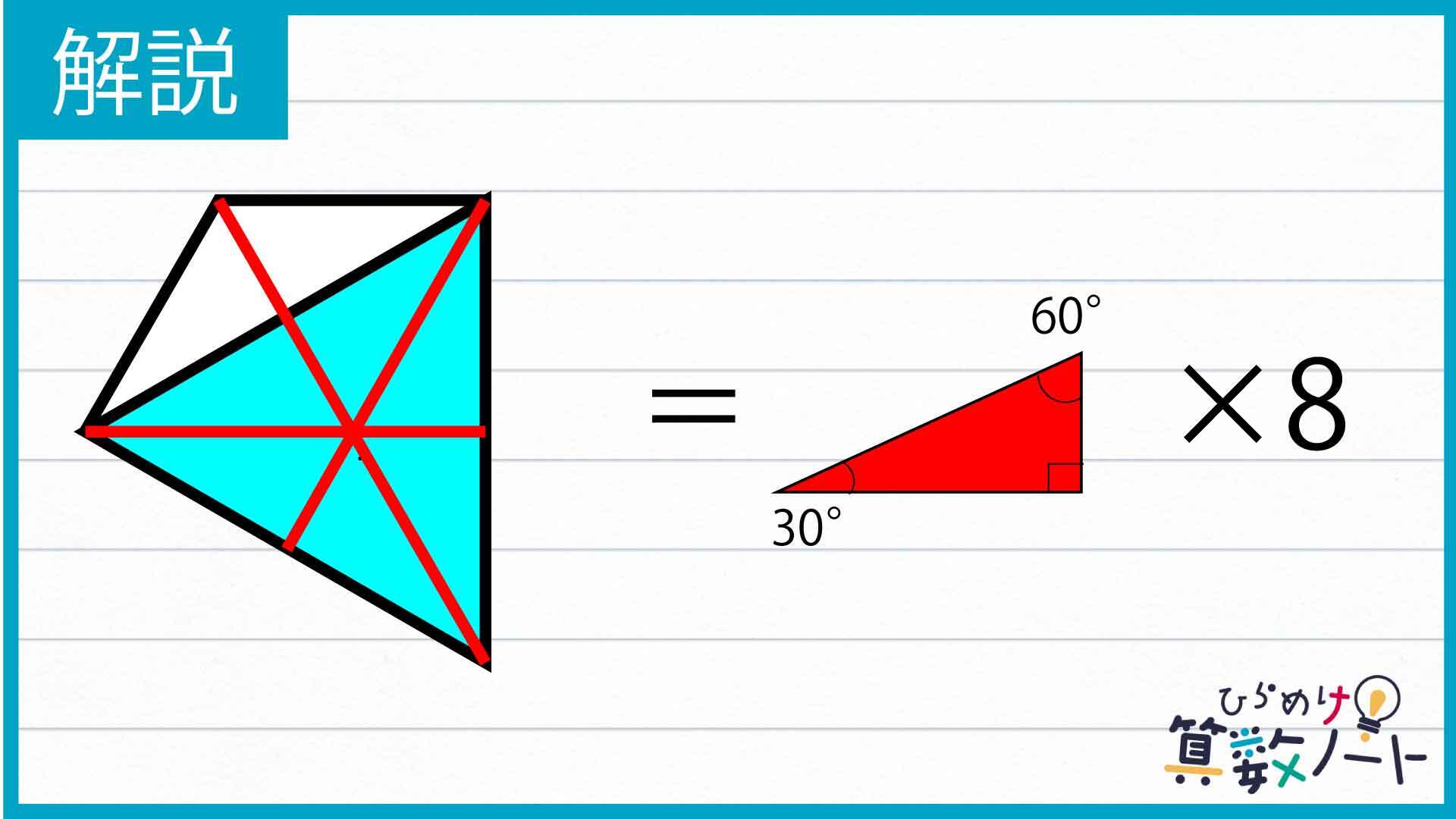
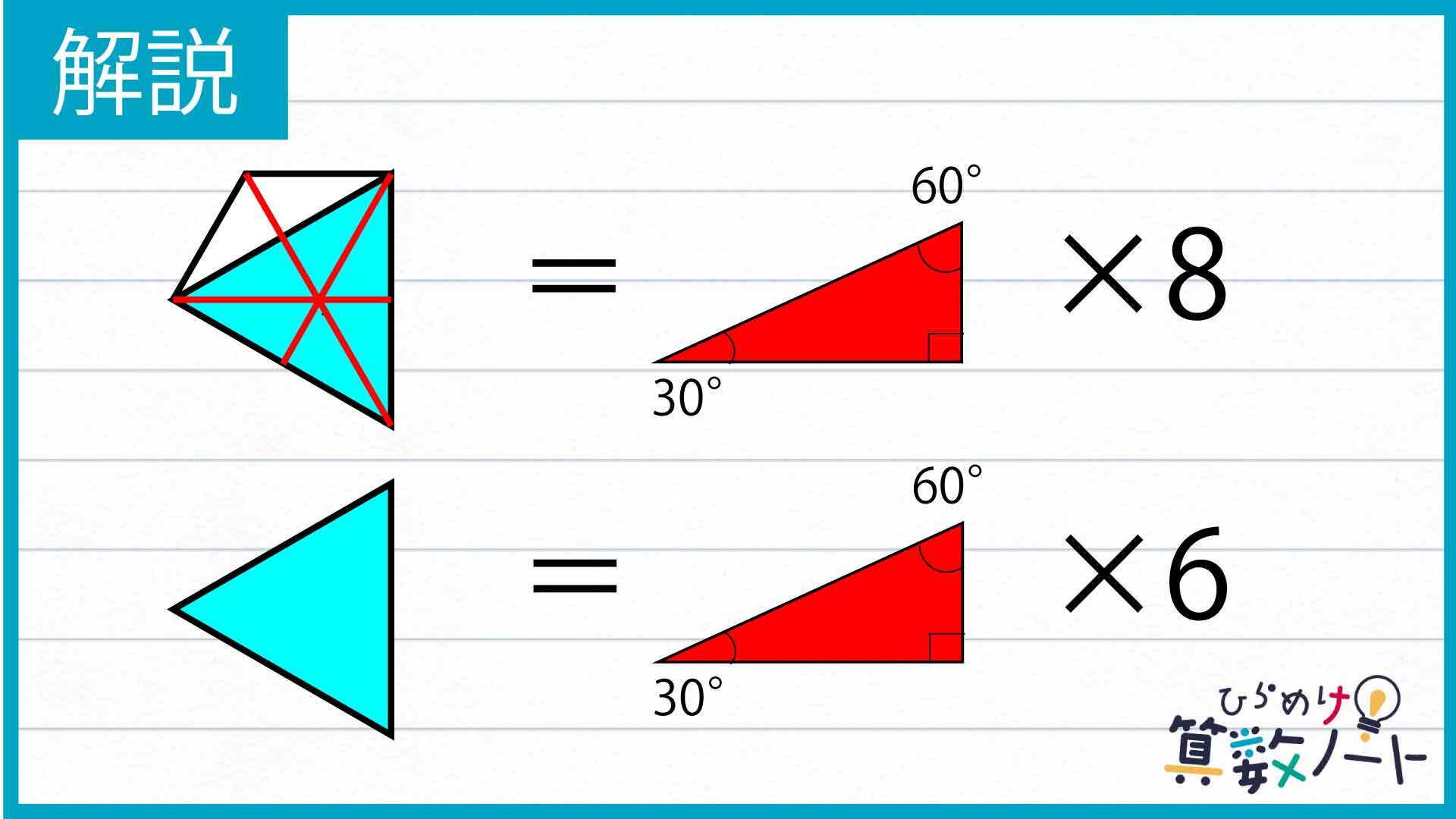
ここで、先ほど注目した図形を下のような赤い線で分割して、8つの三角形を作ります。正六角形の1つの角の大きさは120度であるため、下の図の白い三角形は頂角の大きさが120度の二等辺三角形になります。そのことから、8つの三角形はすべて、内角の大きさが90度、60度、30度の合同な直角三角形であることがわかります。

正六角形を分割してできた直角三角形を活用する

直角三角形の面積を〇とすると、下の図の青い正三角形と白い部分を合わせた部分の面積は8×〇に、青い正三角形の部分の面積は6×〇と表されます。

したがって、下の図の大きい正六角形の面積は「青い正三角形と白い部分を合わせた部分」6つ分であることから6×(8×〇)=48×〇に、小さい正六角形の面積は、青い正三角形6つ分であることから6×(6×〇)=36×〇になります。

そのため、大きい正六角形の面積と小さい正六角形の面積の比は48:36=4:3になります。

大きい正六角形の面積は8cm²なので、求めたい図形の面積は、8×3/4=6cm²となります。

答え：6cm²

「ひらめけ！算数ノート」のバックナンバーはこちら！

【前回の算数ノートはこちら】

【あわせて読みたい】