小学生でも解ける「辺の長さ」を求める問題、あなたは解ける？

解説

それでは解説です。

前ページ：自力で解きたい方はこちらへ！以下は問題の解説です

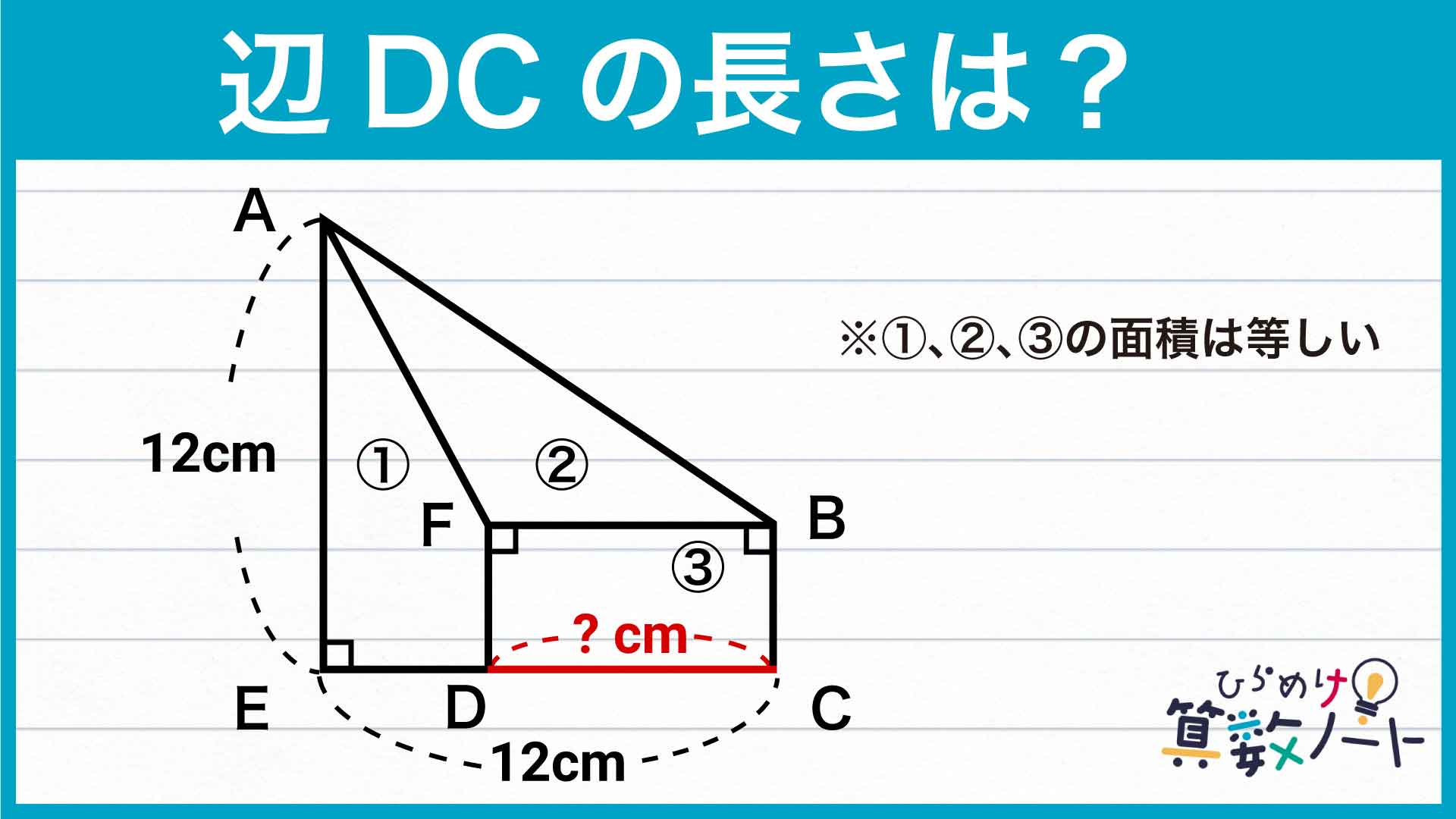
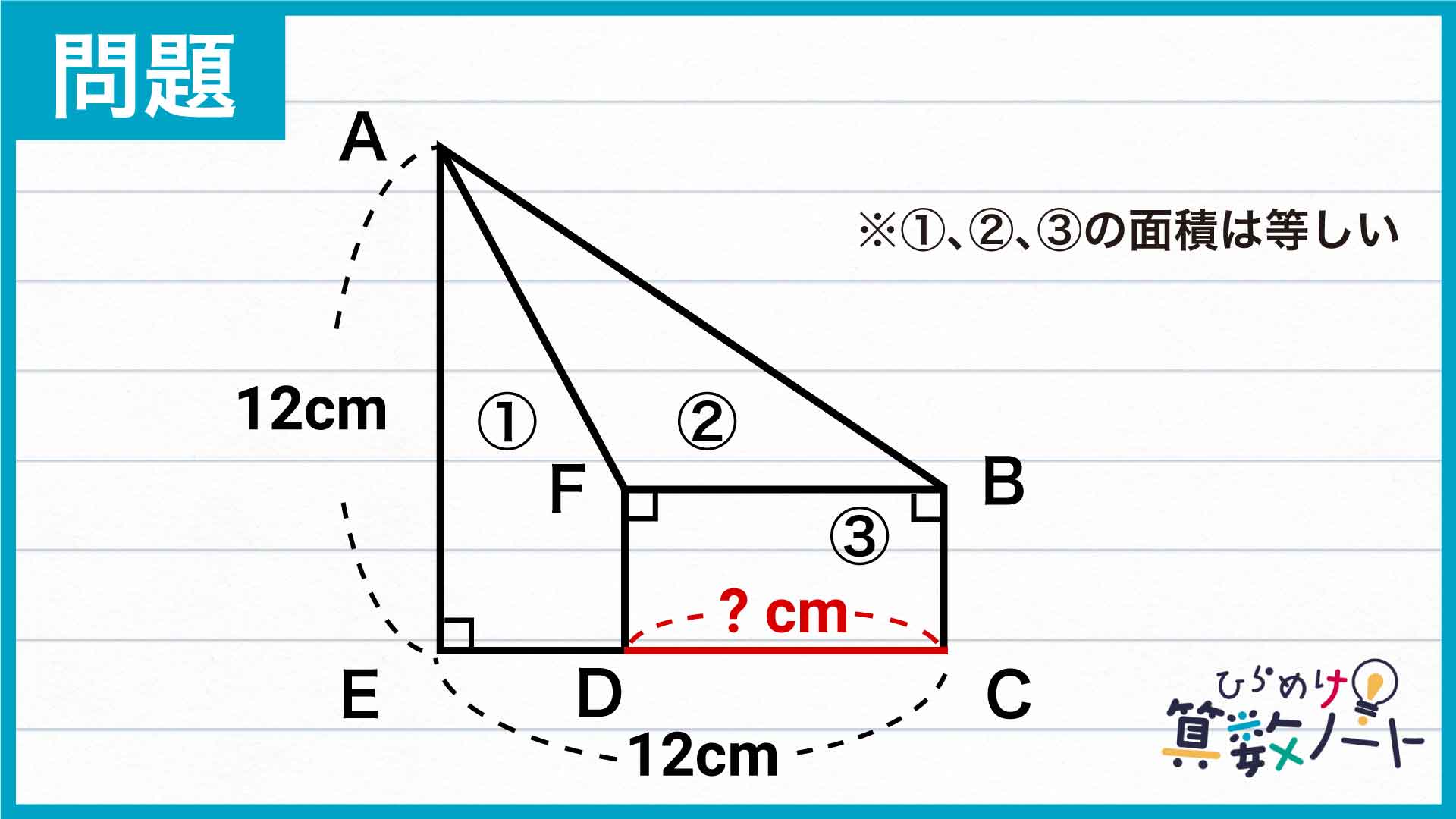
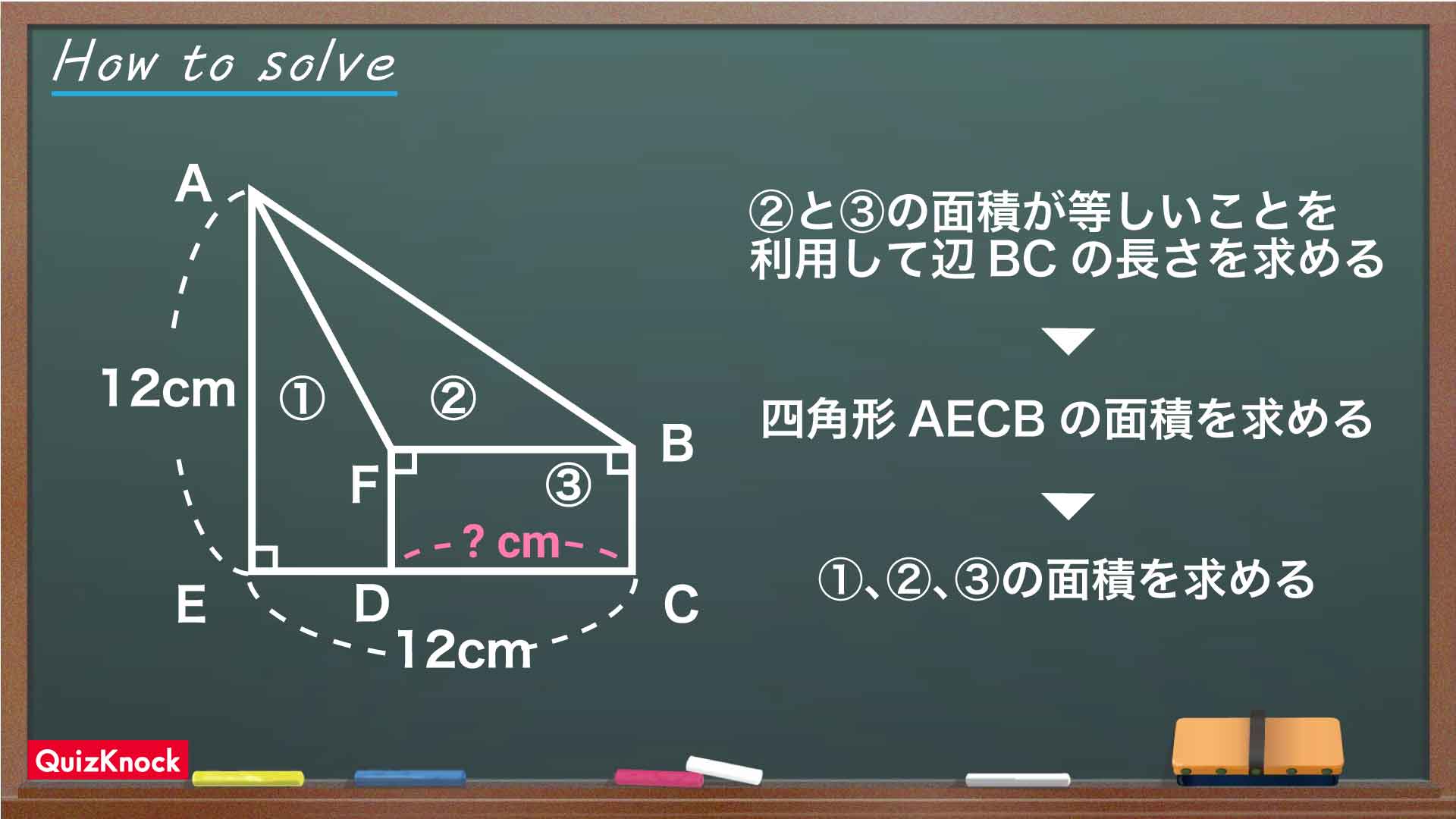
今回の問題の解き方をまとめた図がこちらになります。

BCの長さを求める

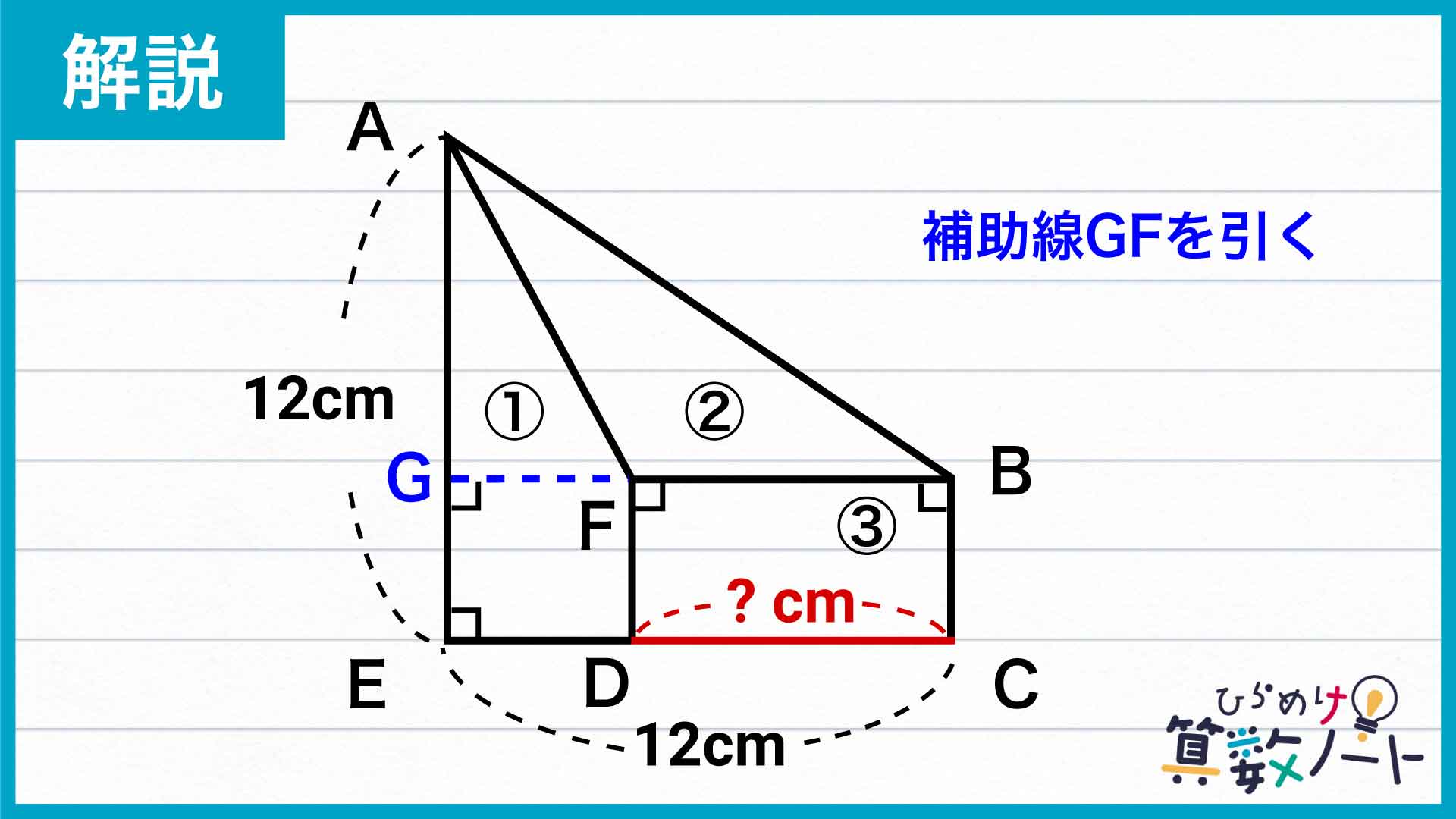
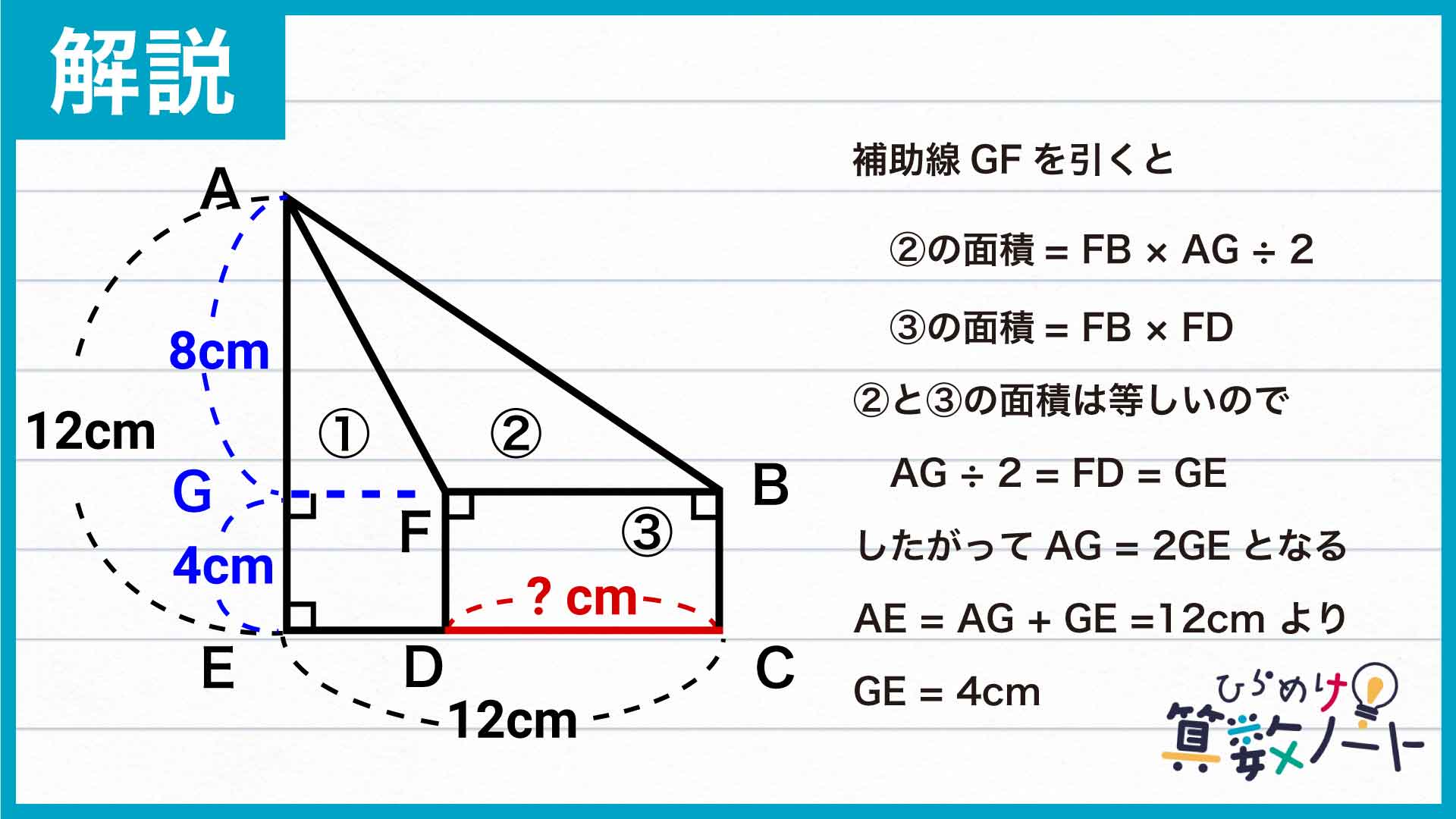
まず、「②と③の面積が等しい」という条件に注目してみましょう。そのために、以下のようにECと平行な補助線GFを引きます。

②の三角形において、FBを底辺と見ると高さはAGになるので、②の三角形の面積はFB×AG÷2と表せます。③の長方形の面積はFB×FDです。FD=GEなので、③の長方形の面積はFB×GEと表せます。

ここで、②と③の面積は等しいため、FB×AG÷2=FB×GEとなります。FBが共通しているため、AG÷2=GEという式が成立します。つまり、「AGの長さはGEの長さの2倍」です。

AG+GE=AE=12cmで、AGの長さはGEの長さの2倍なので、AG=8cm、GE=4cmということがわかります。また、GE=FD=BCなので、FDとBCの長さも4cmです。

四角形AECBの面積を求める

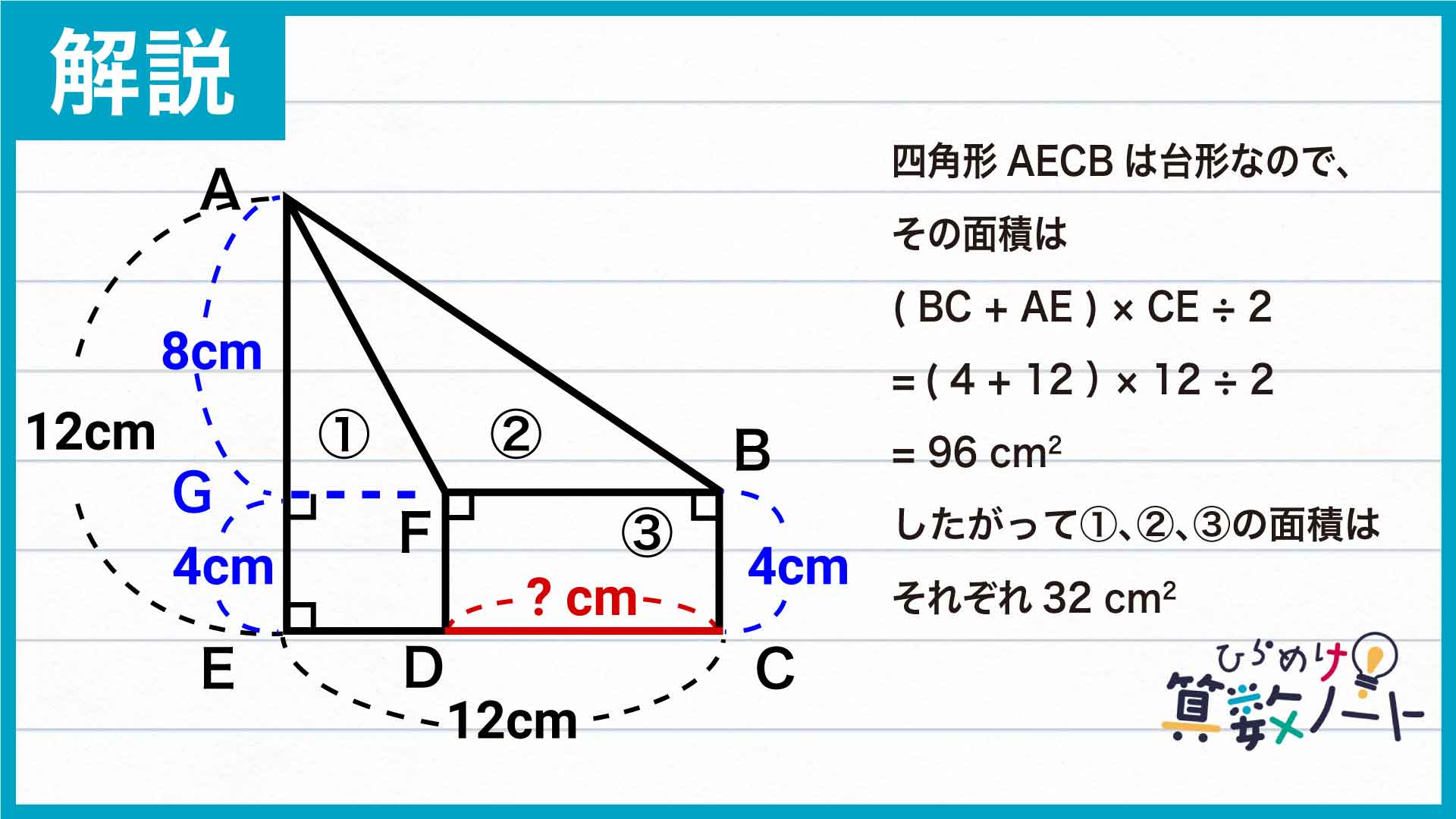
ここで、図形全体に注目します。四角形AECBは台形です。台形の面積は「｛（上底）＋（下底）｝×（高さ）÷２」で求められるので、台形AECBの面積は、(4+12)×12÷2=96cm²です。

①、②、③の面積は等しく、それらを合わせると台形AECBになるので、①、②、③の面積はすべて96÷3=32cm²です。

DCの長さを求める

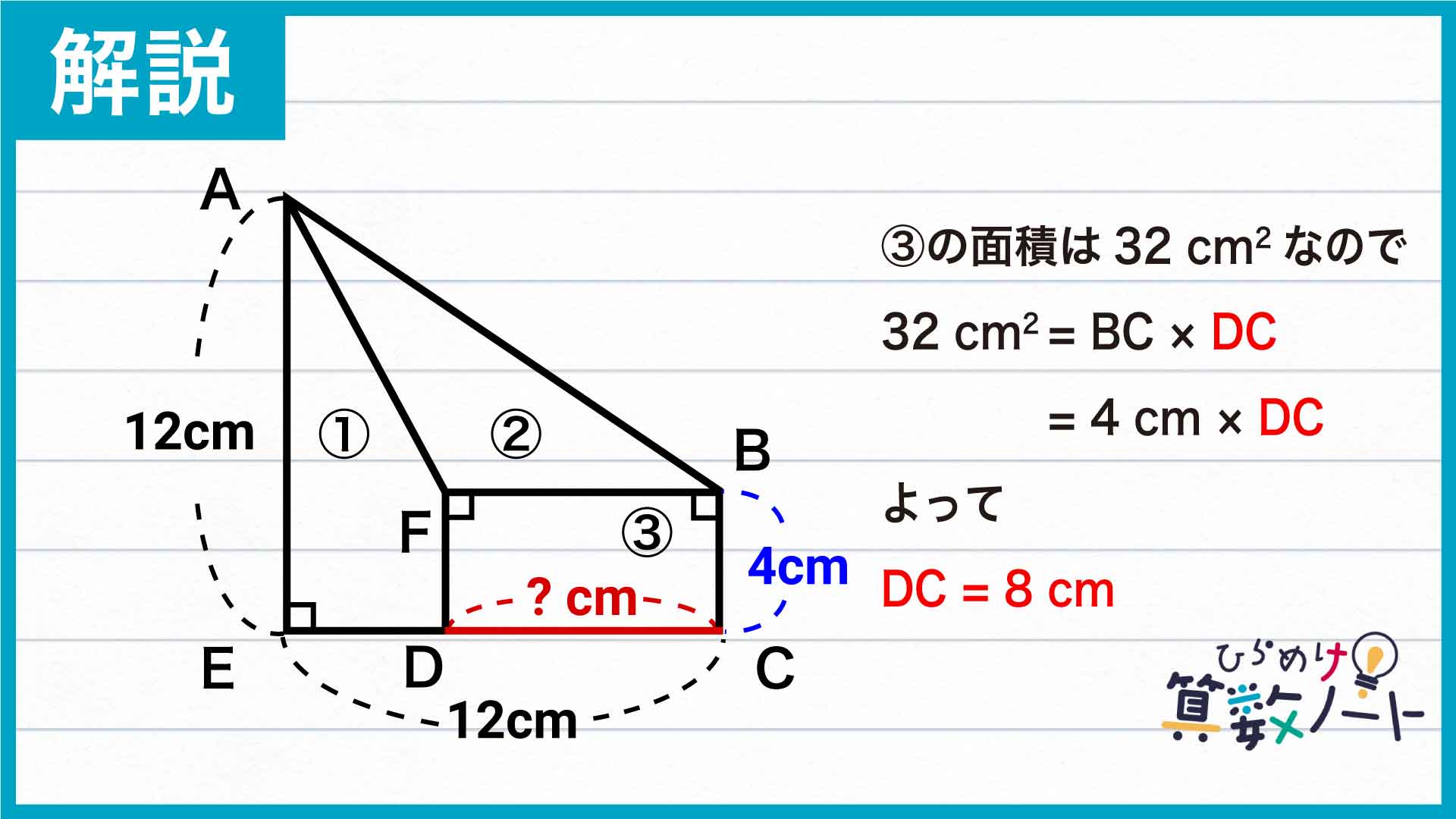
最後に、③の長方形に注目します。③の面積は32cm²で、BC=4cmなので、DCの長さは32÷4=8cmです。

それではまた次の算数ノートでお会いしましょう！

「ひらめけ！算数ノート」のバックナンバーはこちらから！

【前回の算数ノートはこちら】

【あわせて読みたい】